
![]()
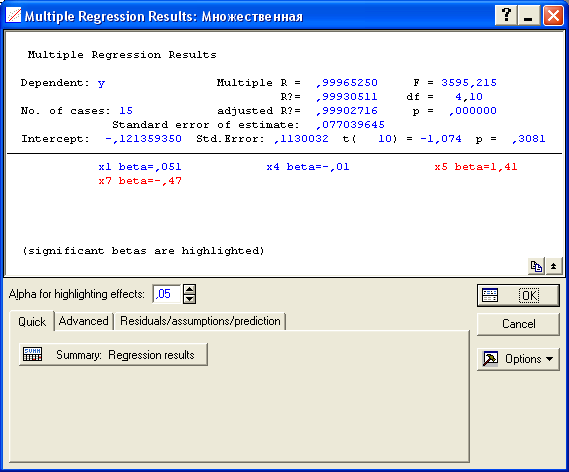
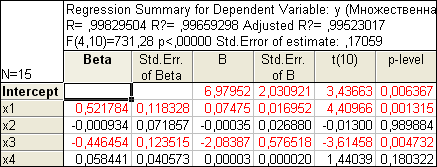
Осуществив переход к результатам регрессии (Summary: Regression results) получаем уравнение линейной множественной регрессии вида y(x1 , x2 , x3 , x4 )=6,9+0,07x1 –0,00035x2 –2,08x3 +0,00003x4 :
 |
2. Если регрессия оказывается значимой, то существует взаимосвязь между параметром у и переменными х1 , х2 ,…,xm . Однако остается неясно, каково влияние конкретных факторов х1 , х2 ,…,xm на исследуемую функцию у . Можно продолжить анализ, используя t- тесты для отдельныхкоэффициентов регрессии а0 , a1 ,a2 ,…,am с целью выяснить, насколько значимой является влияние той или иной переменной х на параметр у при условии, что все другие факторы хk остаются неизменными. Проверку на адекватность коэффициентов регрессии рекомендуется проводить по следующим эквивалентным методам (см. табл. 5).
Таблица 5
| Использование t-критерия Стьюдента | Использование уровня значимости α |
| Анализируемый коэффициент а0 , a1 ,a2 ,…,am считается значимым, если рассчитанное системой Statistica для него значение t -критерия по абсолютной величине превышает tтабл , определяемым с использованием специальных таблиц по заданным уровню значимости (например, a =0,05 ) и числу степеней свободы (df=n-m-1 ). | Коэффициент регрессии а0 , a1 ,a2 ,…,am признается значимым, если рассчитанное системой Statistica для него значение уровня значимости р меньше (или равно) 0,05 (для 95%-ной доверительной вероятности). |
Т.к. вычисленные уровни значимости p-level для коэффициентов, стоящих при x2 и x4 меньше 0,05, то они не значимы. К аналогичному выводу можно прийти, воспользовавшись t -критерием: t2 (10)=-0,013<2,228 и t3 (10)=1,44<2,228.
С учетом этого факта, пересчитаем уравнение множественной регрессии, выбрав в качестве зависимой (dependent ) переменную y и независимые (independent ) переменные х1 и x3 , коэффициенты при которых значимы:
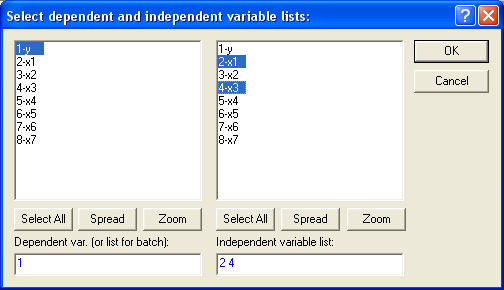
Получаем:
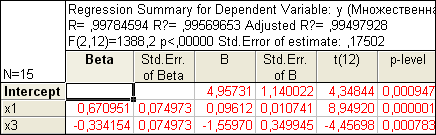
Т.о., уравнение регрессии имеет вид
y(x1 , x3 )=4,957+0,096x1 –1,559x3
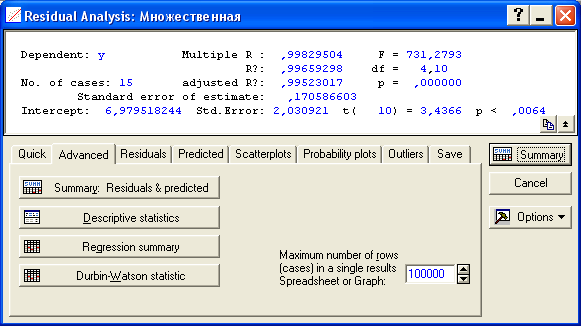
Для выполнения прогнозов по полученному уравнению необходимо показать, что регрессионная модель адекватна результатам наблюдений. С этой целью можно воспользоваться критерием Дарбина-Уотсона, согласно которого, рассчитанный системой Statistica коэффициент dрасч необходимо сравнить с табличным значением dтабл (для совокупности объемом n =15, уровня значимости a = 0,05 и трех оцениваемых параметров регрессии, значение dтаб л =1,75). Если dрасч >dтабл , то полученная модель адекватна и пригодна для прогнозирования. Для определения dрасч в Statistica в окне Residual Analysis на вкладке Advanced необходимо выбрать опцию Durbin-Watson statistic :
![]()
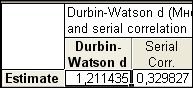
В рассматриваемом примере dрасч =1,2<1,75 , следовательно, модель не желательно использовать для прогнозирования.
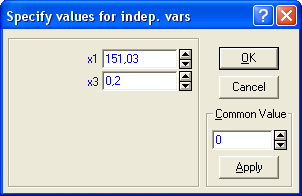
В случае, когда модель адекватна результатам наблюдения для выполнения прогноза в окне Multyple Regression Results
вкладки Residuals/assumptions/prediction
(Остатки/Предположения/Прогнозирование
) выбрать опцию ![]() (прогнозирование зависимой переменной). Например, если в Москве среднегодовую стоимость основных фондов(переменная x1
) повысить на 50 тыс. руб., а трудоемкость единицы продукции (переменная х3
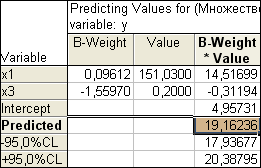
) уменьшить в два раза, то следует ожидать производительности труда равной 19,16 (увеличится на 19,16-14=5,16):
(прогнозирование зависимой переменной). Например, если в Москве среднегодовую стоимость основных фондов(переменная x1
) повысить на 50 тыс. руб., а трудоемкость единицы продукции (переменная х3
) уменьшить в два раза, то следует ожидать производительности труда равной 19,16 (увеличится на 19,16-14=5,16):
2.2 Практическое задание 2. Кластерный анализ в STATISTICA
Постановка задачи
Двадцать банков, акции которых котируются на рынке, предоставили следующую информацию (см. табл.), где – x затраты за прошлый период, y – прибыль за прошлый период.
Необходимо:
1) дополнить таблицу до 20 значений. Данные можно не просто придумать, а взять из любых примеров деятельности банков того или иного города, приведенных в книгах по статистике, эконометрике, СМИ, Internet или любых иных источников.
2) построить график по исходным данным (Scatterplot)
3) c использованием системы STATISTICA выяснить (дать рекомендацию) акции каких банков некоторому предприятию имеет смысл приобрести, каких – придержать, а от каких – избавиться.
Таблица
Номер банка |
Затраты x |
Прибыль y |
| 1 | 4 | 2 |
| 2 | 6 | 10 |
| 3 | 5 | 7 |
| 4 | 12 | 3 |
| 5 | 17 | 4 |
| 6 | 3 | 10 |
| 7 | 6 | 1 |
| 8 | 6 | 3 |
| 9 | 15 | 1 |
| 10 | 15 | 4 |
| 11 | 5 | 4 |
| 12 | 3 | 8 |
| 13 | 13 | 5 |
| 14 | 15 | 3 |
| 15 | 5 | 9 |
Порядок выполнения задания
Кластерный анализ – один из методов статистического многомерного анализа, предназначенный для группировки (кластеризации) совокупности элементов, которые характеризуются многими факторами, и получения однородных групп (кластеров). Задача кластерного анализа состоит в представлении исходной информации об элементах в сжатом виде без ее существенной потери.
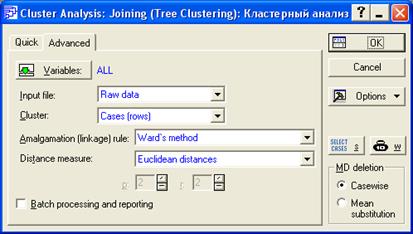
STATISTICA предлагает несколько методов кластерного анализа. В дальнейшем будем использовать Joining (tree clustering ) – группу иерархических методов (7 видов), которые используются в том случае, если число кластеров заранее неизвестно.

Используемый метод – Ward’s method – метод Уорда, который хорошо работает с небольшим количеством элементов и нацелен на выбор кластеров с примерно одинаковым количеством членов. В качестве метрики расстояния пакет предлагает различные меры, но наиболее употребительными являются Euclidean distance (евклидово расстояние). При кластеризации элементов в пакете STATISTICAследует выбирать режим: cases (rows) – строки, а при кластеризации факторов: variables (columns) – столбцы. В качестве переменных для рассматриваемого примере следует выбрать все переменные (all).
Для вывода результатов на экран следует выбрать
![]() либо
либо ![]() .
.
Вывести график на печать.
Проанализировать результат и заполнить таблицу.
Номер банка |
Затраты x |
Прибыль y |
Рекомендация приобрести/придержать/избавиться |
| 1 | 4 | 2 | |
| 2 | 6 | 10 | |
| 3 | 5 | 7 | |
| 4 | 12 | 3 | |
| 5 | 17 | 4 | |
| 6 | 3 | 10 | |
| 7 | 6 | 1 | |
| 8 | 6 | 3 | |
| 9 | 15 | 1 | |
| 10 | 15 | 4 | |
| 11 | 5 | 4 | |
| 12 | 3 | 8 | |
| 13 | 13 | 5 | |
| 14 | 15 | 3 | |
| 15 | 5 | 9 | |
| 16 | |||
| 17 | |||
| 18 | |||
| 19 | |||
| 20 |
8-09-2015, 11:49
