Оглавление:

Введение

1. Основы теории гравитационного вариометра

1.1 Принципы измерения вторых производных потенциала силы тяжести

1.2 Основы теории вариометров

1.3 Основное уравнение вариометра

1.4 Принципиальная схема вариометра

1.5 Гравитационная градиентометрия на подвижном основании

1.6 Спутниковая градиентометрия

2. Гравиметрическая разведка на КМА 2.1 История освоения КМА

2.2 Гравиразведочные работы на железорудных месторождениях

3. Геодезические работы при вариометрической съёмке

3.1 Поправки в наблюденные значения вторых производных 3.2 Требования к точности определения гравиметрических пунктов

Заключение

Список литературы

ВВЕДЕНИЕ

Гравиметрическая разведка полезных ископаемых или гравиразведка является одной из наиболее важных областей практического применения гравиметрических данных. Не случайно основная часть гравиметрических съёмок выполнено с целью гравиметрической разведки.

Гравиразведка применяется на всех этапах геологических, геолого-поисковых работ. При составлении геологических, прогнозных карт разных масштабов, решаются вопросы тектонического районирования прослеживания зон разломов, расчленении свит пород и т. д.

Возможность применения гравиметрической разведки основана на отличии плотности пород изучаемого объекта от плотности окружающих пород. Гравиразведка выявляет геологические структуры форм, благоприят-ных для скопления полезного ископаемого, а также непосредственно залежей полезных ископаемых. [1]

С целью гравиметрической разведки выполняют гравиметровые или вариометрические съёмки. Выделение поля, создаваемого интересуемым аномальным полем, из результатов измерений (так называемые разделения гравитационных полей) выполняют различными способами. В любом из этих способов для определения гравитационного эффекта вмещающих пород необходимо иметь геодезические координаты гравиметрических пунктов. Например, если используют измерения силы тяжести, то для гравиразведки вычисляют аномалии (g - γ) _Б Буге.

(g - γ)_Б = g – γ – 0,0419σΗ,

которая в значительной степени свободна от притяжения топографических масс земной коры.

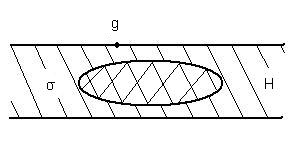
рис 1.

Высота Η гравиметрических пунктов следует знать с точностью, соответствующей точности измерений силы тяжести.

m_h < 10 m _Б ,

где m_h выражена в метрах, а m_Б – в метрах. При точности аномалий Буге в 0,02 мгл допустимая ошибка m_h высот меньше 20 см. Геодезические работы при гравиметрической съёмке является одним из массовых видов работ.

В выпускной работе описаны принципы применения гравиметрических данных для разведки железорудных ископаемых на примере Курской магнитной аномалии. Так как в этом случае основным видом измерений были измерения вторых производных потенциала, изложены принципиальные основы вариометрических и градиентометрических приборов.

1.ОСНОВЫ ТЕОРИИ ГРАВИТАЦИОННОГО ВАРИОМЕТРА И ГРАВИТАЦИОННОГО ГРАДИЕНТОМЕТРА

1.1 Принцип измерения вторых производных потенциала силы тяжести

Сила тяжести в разных точках поверхности Земли различна по величине и направлению.

рис 2.

Выберем в точке А поверхности Земли систему координат А_XYZ : ось Z совместим с направлением силы тяжести, ось X направим на север, ось Y на восток. Согласно определению, первые производные потенциала W силы тяжести равны составляющим силы тяжести по осям координат.

g_X = ∂W/∂x ; g_Y = ∂W/∂yg_Z = ∂W/∂_Z (1.1)

В точке А составляющая g_X равна силе тяжести, а составляющие g_X и g_Y равен нулю. Для точки B направление силы тяжести и оси Z не совпадают, поэтому появляются горизонтальные составляющие g_X и g_Y . Представим их в виде :

(g_X )_B = (g_X )_A + (∂g_X /∂y) x + (∂g_X /∂y)y + (∂g_X /∂z)z

(1.2)

(g_Y )_B = (g_Y )_A + (∂g_Y /∂y) x + (∂g_Y /∂y)y + (∂g_Y /∂z)z

Но согласно (1.1) производные составляющих силы тяжести являются вторыми производными потенциала

∂g_X /∂x = ∂ ² W/∂_X ² ;

∂g_X /∂y = ∂g_Y /∂x = ∂ ² W/∂x∂y ; ∂ ² g/∂y ² = ∂ ² W/∂y ² (1.3)

∂g_Z /∂x = ∂ ² W/∂x∂z ; ∂g_Z /∂y = ∂ ² W/∂x∂z (1.4)

Производные (1.3) связаны с кривизной уровенной поверхности. Их называют градиентами кривизны.

Производные (1.4) называют горизонтальными градиентами силы тяжести.

Уравнение (1.2) поясняет принципиальную возможность измерения вторых производных потенциала : если измерить разности (g_X )_B - (g_X )_A ,

(g_Y )_B - (g_Y )_A составляющих силы тяжести в двух точках, при известных расстояниях X, Y, Z между ними, можно найти входящие в (1.2) коэффициенты. Вторые производные потенциала обычно записывают в виде

∂² W/∂x² =Wxx ∂² W/∂x∂y=Wxy ∂² W/∂x∂z=Wxz

(1.5)

∂² W/∂y² =Wyy ∂² W/∂y∂z=Wyz ∂² W/∂z² =Wzz

Гравитационный вариометр, ориентированный в топоцентрической системе координат X, Y, Z (рис. 2), связанной с гравитационным полем, измеряет компоненты тензора [3]

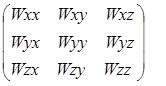(1.6)

Для нахождения компонентов тензора (1.6) измеряют смещение двух или большего числа пробных масс в неоднородном гравитационном поле измерительной системы: при этом полагают, что градиент постоянен в объёме, занятом системой. Разность ускорений, воздействующих на близкие пробные массы, получаются по измерениям разности их перемещений (осевая система с поступательным движением) либо углов поворота (вращательная система). Эти перемещения измеряют оптическими или электрическими устройствами.

1.2. Основы теории вариометров

Основным прибором для нахождения значения почти всех вторых производных потенциала W силы тяжести является гравитационный вариометр. Вариометр разработан венгерским физиком Р. Этвешем в конце XIX века.

Рассмотрим основы теории вариометра. Он представляет собой крутильные весы – прибор для измерения малых сил, действующих в горизонтальной плоскости. На рис. 3 ОО₁ – вертикальная нить, на которой подвешен рычаг AB с грузами массы m на концах. Сила тяжести в точках A, O, B по величине и по направлению различна. Выберем систему прямоугольных координат, начало координат поместим в точку O, ось z направим по касательной к отвесной линии в точки O, ось x – на север, ось y – на восток. Отличие составляющих g_z в точке A и B вызовет наклон коромысла AB в вертикальной плоскости, который при наблюдениях не измеряется и не учитывается. Отличие горизонтальных составляющих в этих точках создаёт пару сил, которые вызовут поворот коромысла в горизонтальной плоскости на угол θ – θ₀ отсчитываемый от положения коромысла в однородном поле.

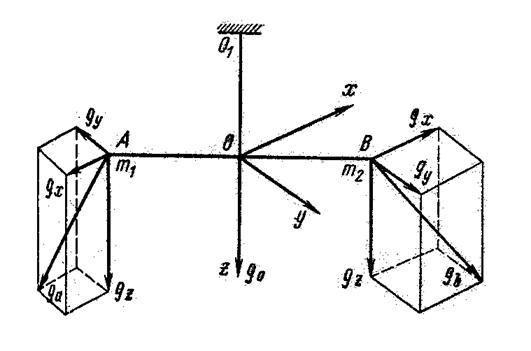
рис. 3

1.3 Основное уравнение вариометра

Напишем уравнение равновесия: τ(θ – θ₀ )+M_Z =0 где τ – крутильная жёсткость нити OO₁ , θ – θ₀ – угол закручивания нити относительно положения равновесия коромысла в однородном поле M_Z – момент внешних сил относительно оси z. Далее по известным формулам получаем основное уравнение гравитационного вариометра

τ(θ – θ₀ )=KW_XY cos2α+K/2Wδsin2α+Lhm(W_XY cosα-W_XY sinα) (1.3.1)

Величина θ – измеренный угол поворота коромысла, α – заданное значение аргумента. Для определения неизвестных нужно выполнить наблюдения в пяти различных азимутах. Если уменьшить длину коромысла, то можно считать K≈0, тогда в основном уравнение останутся только три неизвестных - θ₀ , W_YZ , W_XZ так как произведение W_YZ W_XZ определяют градиент силы тяжести в горизонтальном направлении, то прибор, у которого выполнено условие K≈0 называют градиентометром рис. 4

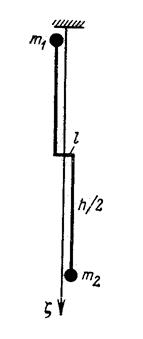рис. 4

Для сокращения времени наблюдения в вариометрах и градинтометрах устанавливают две крутильные системы.

1.4 Принципиальная схема вариометра

В практике гравиразведочных работ наиболее часто применяют вариометры ВГ-1. Вариометр ВГ-1 состоит из трёх основных частей: верхней, средней и нижней. Нижняя - массивная подставка, средняя содержит подъёмные винты, азимутальный круг и автоматическое устройство для поворота верхней части прибора из одного азимута в другой (рис. 5). В верхней – крутильная система и устройство для фотографирования. Оптическая схема вариометра ВГ-1 (рис.6).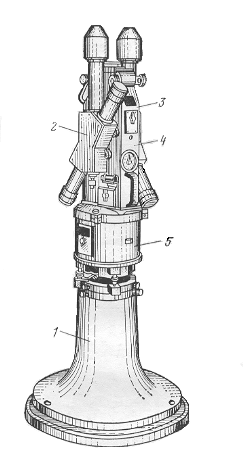

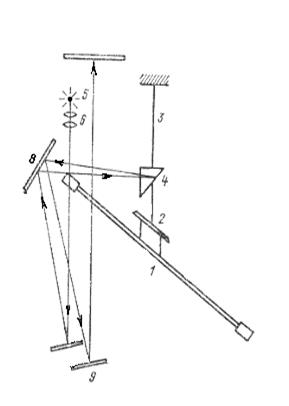
Рис.5 Вариометр S-20 (ВГ-1) Рис. 6 Схема оптической 1- подставка, 2- коробка с системы вариометра ВГ-1 крутильной системой, 3- коробка с оптической системой, 4- верхняя часть, 5- средняя часть

Вариометр ВГ-1 имеет крутильную систему (S- образная). Наклонное коромысло 1 подвешено с помощью бифилярного подвеса 2 на вертикальной нити 3. Для фиксации поворота коромысла на нити 3 укреплена призма 4. Луч света от источника 5 проходит через конденсатор 6 и после отражения от двух неподвижных зеркал 7 и 8 попадает на призму 4. В зависимости от угла закручивания нити 3 луч света после отклонения в призме 4 будет попадатьна разные участки зеркала 8. От зеркала 8 изображение передаётся на фотографическую пластинку 10. Чтобы изображения, полученные при установке коромысла в разных азимутах, не сливались, луч света попадает с зеркала 8 на подвижное зеркало 9, наклон которого автоматически изменяется при изменении азимута коромысла. На неподвижных зеркалах нанесены изображения линий (штрихи). На фотографической пластинке получаются изображения двух штрихов от неподвижных зеркал и блик, фиксирующий положение коромысла. Измерения на пластинке выполняются с помощью дополнительной масштабной шкалы (палетки). Во время измерений верхняя часть прибора устанавливается в нулевой азимут и находится в этом азимуте в течение успокоения коромысла (около 15 минут). Через 13 минут после установки нулевого азимута автоматическое контактное устройство, расположенное в средней части, включает осветитель. Через 2 минуты осветитель выключается и включается ведущий механизм, поворачивающий верхнюю часть прибора в следующий азимут. Поправки в наблюденные значения производных: изменения, вызванные притяжением рельефа и изменением силы тяжести в нормальном поле, учитываются в виде поправок. Поправка за рельеф учитывает влияние масс, расположенных выше и ниже уровенной поверхности точки наблюдения, на вторые производные. Для вычисления поправки за рельеф вокруг пункта наблюдений необходимо выполнить нивелирование в радиусе 50 метров с точностью до 1 см. Для уменьшения влияния рельефа при наблюдениях с вариометрами прибор устанавливают на ровных площадках или при необходимости искусственно выравнивают рельеф вблизи пункта наблюдений. [2]

1.5 Гравитационная градиентометрия на подвижном основании

Измерения градиентов силы тяжести на подвижном основании (автомашине, самолёте) позволяют ускорить локальные, региональные и глобальные исследования гравитационного поля Земли. Градиентометр, не связанный с Землёй, измеряет компоненты тензора V градиентов силы притяжения.

V=grad b=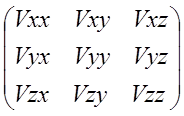(1.5.1)

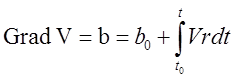(1.5.2)

Главное различие в теории измерений на неподвижном основании и на подвижной, то что при измерении на подвижном основании нужно перейти от топоцентрической системы координат к инерциальной системе. Фирма «Белл» (BellAerospace-Textron, Буффало, Нью-Йорк) разработала систему для градиентометрической съёмки GGSS, предназначенную для работы на автомашине или самолёте. Основными частями системы являются три ортогональных гравитационных градиентометра, установленные с наклоном в 35° на трехосной гироплатформе для непрерывной ориентации в топоцентрической системе координат, связанной с гравитационным полем. Каждый градиентометр содержит две пары акселерометров фирмы Белл (расстояние 0,1 м), установленных ортогонально по краю диска (диаметр 0,2 м); их измерительные оси ориентированы по касательной к диску (рис. 7). Ускорение пробной массы, укрепленной на маятниковом подвесе, измеряется двумя кольцевыми емкостными датчиками, расположенными по обе стороны от этой массы. Выходной сигнал датчиков усиливается и преобразуется в ток. Ток подается в катушку для возвращения пробной массы в нулевое положение.

Система фирмы Белл содержит также приёмоиндикатор спутниковой системы GPS, обеспечивающий в сочетании с акселерометрами и гироплатформой информацию о местоположении и ориентации, блок регистрации данных, компьютер и источник питания (рис. 9). Система с кондиционером предназначена для работы в автомобильном фургоне, который в свою очередь можно разместить в самолете (C-130) для измерений в воздухе.

1.6 Спутниковая градиентоментрия

В настоящее время разрабатываются гравитационные градиентометры, которые основаны на традиционных или сверхпроводящих устройствах и будут установлены на спутниках, планируемых на 1990-е гг. Спутники будут запущены на практически круговые полярные орбиты с высотами от 160 до 250 км. Полагают, что за 6 мес. работы средние значения аномалий силы тяжести (по трапециям 1° х 1° и 0,5° х 0,5°) при разрешении 100— 50 км будут получены с ошибкой ±20 — 50 мкм • с ^-2 . Приведем примеры разработок, основанных на разных принципах..

Французская программа GRADlO (Национальное бюро по аэродинамическим исследованиям и Исследовательская группа по космической геодезии) предусматривает создание градиентометра на базе традиционной технологии. В этом приборе имеется несколько микроакселерометров, которые расположены симметрично относительно центра масс по углам многоугольника так, что можно определить полный гравитационный тензор. Трехосные электростатические акселерометры должны иметь разрешение 10 ^{- 12} м • с ^{- 2} .При максимальных возмущающих ускорениях около 10 ^{- 4} м • с ^{- 2} (на высоте 200км) прибор должен иметь динамический измерительный диапазон 10 ⁸ ; для непрерывного контроля и калибровки акселерометров предусмотрена бортовая калибровочная система.

Примером сверхпроводящего градиентометра является прибор Пайка, созданный в Университете штата Мэриленд, США. Основными элементами этой невращающейся системы служат сверхпроводящие акселерометры. Акселерометр содержит пробную массу на мягком подвесе, магнитный преобразователь и усилитель с низкими шумами (сверхпроводящее квантовое интерференционное устройство сквид — SQUID) в состоянии сверхпроводимости. Магнитное поле, создаваемое катушками преобразователя, модулируется при движении пробной массы, в сквиде происходит детектирование и усиление модулирующего сигнала, который затем преобразуется в выходное электрическое напряжение.

Сверхпроводящая схема позволяет непосредственно суммировать и вычитать сигналы акселерометров. Это в свою очередь дает возможность измерять компоненты тензора градиентов силы тяжести, а также линейные и угловые ускорения носителя, необходимые для вычисления поправок. В системах с продольным расположением акселерометров сигналы пропорциональны диагональным элементам V_ii тензора и линейным (поступательным) ускорениям. Системы же с перекрестным расположением акселерометров дают недиагональные элементы и угловые (вращательные) ускорения (рис. 10).

2. ГРАВИМЕТРИЧЕСКАЯ РАЗВЕДКА НА КУРСКОЙ МАГНИТНОЙ АНОМАЛИИ

2.1 История освоения КМА

Впервые КМА обнаружил ещё в 1783 г. П.Б. Иноходцев. Эта аномалия самая большая в мире: напряжённость магнитного поля там иногда в 5 и более раз превышает нормальную. Но только через столетие началось настоящее изучение этой аномалии. Наибольшую работу по изучению Курской аномалии осуществил Э.Е. Лейст, работавший там около 30 лет с начала 90х годов до 1918 г. и измеривший весьма точно поле в 4500 пунктов. В последний год он жаловался, что ему мешали работать крестьяне, принимавшие его за землемера и заставлявшие его проводить делёж помещичьих земель. В 1918 г. Э.Е. Лейст уехал в Германию и увёз с собой все материалы по Курской аномалии. Он вскоре умер.

В 1919 г. по предложению В.И. Ленина была организованна особая комиссия под председательством П.П. Лазарева по исследованию Курских магнитных аномалий. В1919 г. П.П. Лазарев 12 раз собирал свою комиссию для обсуждения плана работ. Комиссия прежде всего затребовала у наследников умершего проф. Э.Е. Лейста его материалы по магнитной съёмке, но они запросили за них 1 миллион долларов. При изучении этого материала выяснилось, что хотя проф. Лейст и весьма точно измерил компоненты магнитного поля, но координаты пунктов были определены очень неточно, а магнитное поле менялось так сильно в зависимости от положения точки, что наблюдения Лейста в значительной мере потеряли свою ценность. Важно было иметь не столь точные значения поля, но более точные положения точек.

Было решено делать съёмку. Изготовлять много магнитометров было длительным делом, и А.Н. Крылов, который в начале своей деятельности занимался теорией морских магнитных компасов по военно-морскому ведомству, предложил использовать эти компасы, позволяющие определить все компоненты магнитного поля. Предложение А.Н. Крылова приняли и за два года съёмки была в основном сделана и лучше, чем у Лейста. К проведению её были привлечены студенты Московского университета.

Кроме магнитных, геологических и буровых работ комиссия решила впервые широко использовать гравиметрический метод разведки. Для использования маятникового метода был приглашён А.А. Михайлов, а для работы с гравитационным вариометром Этвеша – П.М. Никифоров.

Первая попытка найти гравитационную аномалию в Курской области была сделана Иоганном Фридрихом фон Парротом в первой четверти XIX в. Метод Паррота был принципиально прост – сравнивалось изменение атмосферного давления, измеренное на соседних точках двумя приборами: анероидом и ртутным барометром. Паррот получил разницу в 0,17 мм ртутного столба, что соответствовало огромной аномалии, примерно на 2 порядка большей, чем впоследствии выяснилось из настоящих гравитационных наблюдений.

Ранее маятниковые наблюдения силы тяжести проводились только в теплоизолированных помещениях на солидных каменных столбах и длительное время. На КМА надо было измерять силу тяжести в поле на профилях протяжённостью всего 3-5 км, где не было зданий. А.А. предложил метод наблюдений в выкопанных траншеях глубиной 1,5 м и длинной в 4 м, закрытых изолирующей двойной фанерной палаткой (рис. 11).

В таких траншеях в одном конце вкапывался тяжёлый медный колокол, заменявший цементный столб для установки маятникового прибора. В другом конце размещался наблюдатель с приёмным устройством и контактным хронометром. Поправки времени для этих часов определялись уже по ритмическим радиосигналам, только недавно ставшим входить в обиход астрономических наблюдений. В результате разработанной методики наблюдений в поле точность определения была около 1,5 мГал (маятник Штюкрата), что позволило уверенно определить аномалии в 10 мГал на профилях длиною 4-6 км. 1921 г. – в районе Щигров 1922 г. – в районе Салтыковки 1923 г. – в районе Щигров 1924 г. – в районе Белгородского уезда 1925 г. – в районе Тима

Основным наблюдателем был сам А.А. Кроме приёма сигналов времени из Москвы и Науэна А.А. Михайлов определял также поправки часов астрономически.

Он же проводил геодезические определения координат пунктов наблюдений путём привязки к ближайшим геодезическим знакам и астрономические определения координат с помощью универсальных инструментов. Благодаря исключительному мастерству А.А. как наблюдателя ему удалось даже определить уклонение отвеса, вызываемые тяжёлыми магнитными массами, хотя эти уклонения были очень малы – порядка 1 секунды дуги.В


29-04-2015, 00:28