Министерство образования и науки Республики Казахстан
Западно-Казахстанский аграрно-технический университет
имени Жангир хана
Кафедра: «Разработки и эксплуатации нефтегазовых месторождений»
РЕФЕРАТ
по дисциплине «Подземная гидромеханика»
на тему
«Границы применимости закона Дарси. Нелинейные законы фильтрации»
Выполнил: студент гр.НГДБ-24
Изтелеуов К.А
Проверил: профессор
Курмангалиев Р.М.
Уральск 2010
Содержание
Введение
1. Верхняя граница применимости закона Дарси
2. Отклонения от закона Дарси при малых скоростях фильтрации
Список литературы
Введение
Проверке и исследованию пределов применимости закона Дарси посвящено значительное число работ отечественных и зарубежных специалистов. В процессе этих исследований показано, что можно выделить верхнюю и нижнюю границы применимости закона Дарси и соответствующие им две основные группы причин.
1) Верхняя граница определяется группой причин, связанных с проявлением инерционных сил при достаточно высоких скоростях фильтрации.
2) Нижняя граница определяется проявлением неньютоновских реологических свойств жидкости, ее взаимодействием с твердым скелетом пористой среды при достаточно малых скоростях фильтрации.
Рассмотрим каждый из этих предельных случаев, которые приводят к нелинейным законам фильтрации.
1. Верхняя граница применимости закона Дарси
Наиболее полно изучены отклонения от закона Дарси, вызванные проявлением инерционных сил при увеличении скорости фильтрации. Верхнюю границу применимости закона Дарси связывают обычно с некоторым критическим (предельным) значением ![]() числа Рейнольдса1
числа Рейнольдса1
![]()
где d- некоторый характерный линейный размер пористой среды; v-кинематический коэффициент вязкости флюида ![]()
Многочисленные экспериментальные исследования и, в частности, опыты Дж. Фэнчера, Дж. Льюиса и К. Бернса, Линдквиста, Г. Ф. Требина, Н.М. Жаворонкова, М.Э. Аэрова и других были направлены на построение универсальной зависимости (по аналогии с трубной гидравликой) коэффициента гидравлического сопротивления l от числа Рейнольдса. Однако вследствие различной структуры и состава пористых сред получить такую универсальную зависимость не удается.
При обработке результатов экспериментов значительное внимание обращалось на такой выбор характерного размера поровой структуры, чтобы отклонения от закона Дарси возникали при одинаковых значениях числа Рейнольдса, и закон фильтрации в нелинейной области допускал универсальное представление.
Первая количественная оценка верхней границы применимости закона Дарси была дана более 60 лет назад Н. Н. Павловским, который, опираясь на результаты Ч. Слихтера, полученные для модели идеального грунта, и полагая характерный размер d равным эффективному диаметру dэф вывел следующую формулу для числа Рейнольдса
![]() (1.11)
(1.11)
Использовав эту формулу и данные экспериментов, Н.Н. Павловский установил, что критическое значение числа Рейнольдса находится в пределах
![]()
Достаточно узкий диапазон изменения значений Reкр объясняется тем, что в опытах использовались не слишком разнообразные образцы пористых сред.
Для удобства обработки результатов многочисленных экспериментов различных авторов В. Н. Щелкачев предложил использовать безразмерный параметр, названный им параметром Дарси и определяемый равенством
![]() (1.12)
(1.12)

Отсюда видно, что параметр Дарси представляет собой отношение силы вязкого трения к силе давления. Сравнивая равенство (1.12) и закон Дарси (1.7) (для случая горизонтального пласта, когда р* = р), можно утверждать, что если справедлив закон Дарси, то
![]() (1.13)
(1.13)
Таким образом, равенство (1.13) должно выполняться при ![]()
Введение параметра ![]() упрощает исследование границы применимости линейного закона фильтрации. Действительно, если на оси абсцисс откладывать
упрощает исследование границы применимости линейного закона фильтрации. Действительно, если на оси абсцисс откладывать ![]() а по оси ординат
а по оси ординат ![]() то поскольку
то поскольку ![]() при
при ![]() графиком зависимости
графиком зависимости ![]() от
от ![]() будет прямая линия, совпадающая с осью абсцисс до тех пор, пока
будет прямая линия, совпадающая с осью абсцисс до тех пор, пока ![]() .
.
Как только на этом графике линия начнет отделяться от оси абсцисс, сразу же обнаружится нарушение закона Дарси (это соответствует значениям ![]() ). Значение
). Значение ![]() при котором станет заметно отклонение упомянутой линии от оси абсцисс, и будет критическим значением. Для иллюстрации сказанного на рис. 1.5 на логарифмической сетке приведены зависимости
при котором станет заметно отклонение упомянутой линии от оси абсцисс, и будет критическим значением. Для иллюстрации сказанного на рис. 1.5 на логарифмической сетке приведены зависимости ![]() от
от ![]() , представляющие результат обработки опытов по формулам В. Н. Щелкачева (табл. 1.1). Данные на этом графике соответствуют области нелинейной фильтрации
, представляющие результат обработки опытов по формулам В. Н. Щелкачева (табл. 1.1). Данные на этом графике соответствуют области нелинейной фильтрации ![]() для различных образцов пористых сред.
для различных образцов пористых сред.
Основываясь на этих соображениях, В. Н. Щелкачев провел критический анализ и сравнение формул, полученных разными исследователями, для определения ![]() в подземной гидромеханике и оценки возможных критических значений числа Рейнольдса
в подземной гидромеханике и оценки возможных критических значений числа Рейнольдса ![]() соответствующих верхней границе применимости закона Дарси. Результаты такого сопоставления приведены в табл. 1.1. В первых двух строках таблицы даны соответственно формулы для
соответствующих верхней границе применимости закона Дарси. Результаты такого сопоставления приведены в табл. 1.1. В первых двух строках таблицы даны соответственно формулы для ![]() и коэффициента гидравлического сопротивления l, полученные разными авторами. В четвертой и пятой строках приведены соответственно критические значения
и коэффициента гидравлического сопротивления l, полученные разными авторами. В четвертой и пятой строках приведены соответственно критические значения ![]() полученные самими авторами, и их уточненные значения.
полученные самими авторами, и их уточненные значения.
Наличие третьей строки табл. 1.1, в которой дано произведение ![]() объясняется следующим. В области линейного закона фильтрации
объясняется следующим. В области линейного закона фильтрации ![]() справедливо равенство (1.13). Поэтому если произведение
справедливо равенство (1.13). Поэтому если произведение ![]() зависит только от параметра
зависит только от параметра ![]() (см. графы 5-8 табл. 1.1), то оно имеет постоянное значение (не зависящее от свойств пористой среды) в случае, если
(см. графы 5-8 табл. 1.1), то оно имеет постоянное значение (не зависящее от свойств пористой среды) в случае, если ![]() И только в этом случае можно получить «универсальный» прямолинейный график в координатах
И только в этом случае можно получить «универсальный» прямолинейный график в координатах ![]() соответствующий фильтрации различных флюидов через различные по свойствам пористые среды. Результаты обработки опытов подтверждают этот вывод.
соответствующий фильтрации различных флюидов через различные по свойствам пористые среды. Результаты обработки опытов подтверждают этот вывод.
На основе анализа данных, приведенных в табл. 1.1, можно сделать следующие выводы.
1. Несмотря на отмеченные недостатки результатов Н. Н. Павловского, есть основания для их сопоставления с соответствующими результатами трубной гидравлики. Важно подчеркнуть, что критические значения числа Рейнольдса, подсчитанные по формуле (1.11), намного меньше тех, которые в трубной гидравлике соответствуют переходу ламинарного течения в турбулентное. Это служит одним из доводов в пользу того, что причины нарушения закона Дарси при высоких скоростях фильтрации (увеличение влияния сил инерции по мере увеличения ![]() ) не следует связывать с турбулизацией течения. Отсутствие турбулентности при нарушении закона Дарси было доказано также прямыми опытами, изложенными Г. Шнебели.
) не следует связывать с турбулизацией течения. Отсутствие турбулентности при нарушении закона Дарси было доказано также прямыми опытами, изложенными Г. Шнебели.
Формулы Фэнчера, Льюиса и Бернса получены формальным введением в выражение для числа Рейнольдса эффективного диаметра ![]() в качестве характерного размера пористой среды, они не сопоставимы с результатами трубной гидравлики, дают слишком узкий диапазон изменения значений
в качестве характерного размера пористой среды, они не сопоставимы с результатами трубной гидравлики, дают слишком узкий диапазон изменения значений ![]() (см. графу 4 табл. 1.1), мало обоснованы.
(см. графу 4 табл. 1.1), мало обоснованы.
2. Во все другие формулы табл. 1.1 (графы 5-9) в качестве характерного размера входят величины, пропорциональные ![]() (где k-коэффициент проницаемости породы), методы определения которых хорошо известны. Формулы этой группы не имеют принципиальных преимуществ и одинаково удобны для практического использования. Для этих формул характерно то, что все они приводят к очень широким диапазонам изменения
(где k-коэффициент проницаемости породы), методы определения которых хорошо известны. Формулы этой группы не имеют принципиальных преимуществ и одинаково удобны для практического использования. Для этих формул характерно то, что все они приводят к очень широким диапазонам изменения ![]() для различных пористых сред. И это представляется вполне естественным ввиду разнообразия свойств испытанных пористых сред. Кроме того, это свидетельствует о том, что ни в одну из предложенных формул для определения
для различных пористых сред. И это представляется вполне естественным ввиду разнообразия свойств испытанных пористых сред. Кроме того, это свидетельствует о том, что ни в одну из предложенных формул для определения ![]() не входит полный набор параметров, позволяющий характеризовать сложную структуру пористых сред, использования для этой цели коэффициентов пористости проницаемости явно недостаточно.
не входит полный набор параметров, позволяющий характеризовать сложную структуру пористых сред, использования для этой цели коэффициентов пористости проницаемости явно недостаточно.
Вместе с тем, широкий диапазон изменения значений ![]() можно разбить на сравнительно узкие интервалы, соответствующие различным группам образцов пористых сред. Это облегчает указание возможной верхней границы справедливости закона Дарси при движении флюида в какой-либо пористой среде.
можно разбить на сравнительно узкие интервалы, соответствующие различным группам образцов пористых сред. Это облегчает указание возможной верхней границы справедливости закона Дарси при движении флюида в какой-либо пористой среде.
Результаты такого разбиения для формулы В. Н. Щелкачева (см. табл. 1.1, первая строка, пятая графа) приведены в табл. 1.2.
Итак, при значениях числа Рейнольдса ![]() линейный закон Дарси перестает быть справедливым. Первое обобщение закона Дарси на случай больших
линейный закон Дарси перестает быть справедливым. Первое обобщение закона Дарси на случай больших ![]() основанное на опытных данных, было выполнено Дюпюи, который сформулировал двучленный закон.
основанное на опытных данных, было выполнено Дюпюи, который сформулировал двучленный закон.
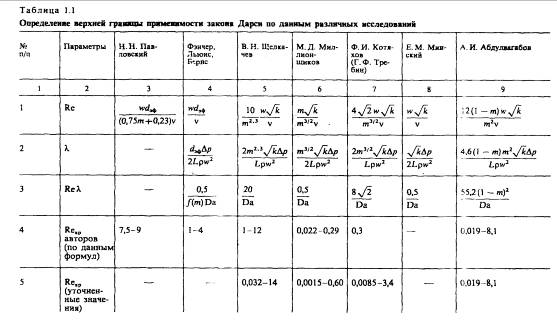
Таблица 1.2
Интервалы критических значений ![]() для образцов пористых сред
для образцов пористых сред
№ п/п |
Образец пористой среды | Диапазон критических значений |
| 1. | Однородная дробь | 13-14 |
| 2. | Однородный крупнозернистый песок | 3-10 |
| 3. | Неоднородный мелкозернистый песок с преобладанием фракций диаметром менее 0,1 мм | 0,34-0,24 |
| 4. | Сцементированный песчаник | 0,05-104 |
фильтрации, носящий имя австрийского исследователя Ф. Форхгеймера, независимо установившего его несколько позднее. В принятых сейчас обозначениях это соотношение можно представить (для простейшего случая прямолинейно-параллельного течения без учета силы тяжести) в следующем виде:
![]() (1.14)
(1.14)
где b - дополнительная константа пористой среды, определяемая экспериментально.
Первое слагаемое в правой части (1.14) учитывает потери давления вследствие вязкости жидкости, второе - инерционную составляющую сопротивления движению жидкости, связанную с криволинейностью и извилистостью поровых каналов. Из (1.14) следует, что при малых скоростях фильтрации квадратом скорости w2 можно пренебречь, и градиент давления будет зависеть только от первого слагаемого, т.е. движение будет безынерционным, соответствующим закону Дарси. При больших скоростях фильтрации силы инерции становятся существенными и будут сопоставимы или даже преобладать над силами вязкости.
Хорошая согласованность соотношения (1.14) с данными промысловых и экспериментальных наблюдений была установлена в много численных работах советских и зарубежных исследователей. Это свидетельствует о том, что данное соотношение представляет нечто большее, чем простую эмпирическую формулу, поскольку оно хорошо выполняется даже для весьма больших значений скорости фильтрации. Физический смысл этого заключается в том, что при больших скоростях быстропеременное движение в порах вследствие «извилистости» поровых каналов сопряжено с появлением значительных инерционных составляющих гидравлического сопротивления. С увеличением числа Рейнольдса квадратичный член в выражении (1.14) оказывается преобладающим, силы вязкости пренебрежимо малы по сравнению с силамиинерции, и (1.14) сводится тогда к квадратичному закону фильтрации, предложенному А. А. раснопольским. Он справедлив в средах, состоящих из частиц достаточно крупных размеров.
2. Отклонения от закона Дарси при малых скоростях фильтрации
В опытах, проведенных в конце прошлого века с тонкозернистыми грунтами при малых скоростях, было обнаружено увеличение скорости фильтрации с ростом градиента давления более быстрое, что это дает линейный закон Дарси. Однако объяснение этого факта не приводилось.
Начиная с 50-х годов XX в. появилось большое число теоретических и экспериментальных работ, подтвердивших нарушения закона Дарси в области малых скоростей. Это явление заметнее всего при движении воды в глинах, но наблюдается также и при фильтрации в песках и песчаниках не только воды, но и нефтей. При этом во всех экспериментах обнаруживалась существенная нелинейность закона фильтрации при малых скоростях.
Объяснение этого явления заключается в том, что при малых скоростях фильтрации становится существенным силовое взаимодействие между твердым скелетом породы и фильтрующимся флюидом, которое может дать преобладающий вклад в фильтрационное сопротивление. При весьма малых скоростях потока сила всякого трения кренобразного мало, тогда как сила межфазового взаимодействия остается при этом конечной величиной, поскольку она не зависит от скорости и определяется только свойствами контактирующих фаз. В результате такого взаимодействия нефть, содержащая поверхностно-активные компоненты, в присутствии пористого тела с развитой поверхностью образует устойчивые коллоидные растворы (студнеобразные пленки), частично пли полностью перекрывающие поры. Чтобы началось движение, нужно разрушить эту структуру, приложив некоторый перепад давления. В случае фильтрации воды в глинизированных породах аналогичные соображения относятся к образованию коллоидных глинистых растворим, при этом структурообразующий компонент-глинистые частицы можно заимствовать из самого материала твердого скелета.
Приведенные факты показывают, что многие жидкости (нефть, пластовая вода). не проявляющие аномальных свойств вне контакта с пористой средой, при малых скоростях фильтрации могут образовывать неньютоновские системы, взаимодействуя с пористой породой. Наличие начального градиента давления g, при достижении которого начинается фильтрации, было обнаружено и при движении флюидов в газовода насыщенных пористых средах. При этом было установлена, в изменяется широких пределах и в большинстве случаев тем выше, чем больше глинистого материала содержится в пористой среде и чем выше остаточная вода насыщенность газо-водяной смеси.
Наряду с этим неньютоновские свойства пластовых нефтей с повышенном содержанием высокомолекулярных компонентов (смол, асфальтенов и.т.) могут проявляется в широком диапазоне изменения скоростей.
Список литературы
Подземная гидравлика. К.С. Басниев, А.М. Власов, В.М. Максимов «Недра» Москва 1993 г.
Подземная гидромеханика. К.С. Басниев, Н.М. Дмитриев, Г.Д. Розенберг Москва 2005 г.
29-04-2015, 00:35
