Угловые элементы внешнего ориентирования снимков wi , ai , Ài определяют в следующей последовательности:
1. Сначала получают матрицу преобразования координат i-го снимка
![]() ; ( 2)
; ( 2)
АМ – матрица, в которой элементы aij вычисляют по угловым элементам внешнего ориентирования модели wМ , aМ , ÀМ ;
Ai ’ – матрица, в которой элементы aij вычисляют по угловым элементам взаимного ориентирования i-го снимка wi ’, ai ’, Ài ’.
2. Затем по элементам aij матрицы Ai вычисляют угловые элементы внешнего ориентирования i-го снимка стереопары:
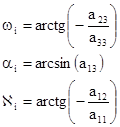 .
.
10. Точность определения координат точек объекта по стереопаре снимков
Для предрасчета точности определения координат точек местности по стереопаре аэрофотоснимков, учитывая, что углы наклона снимков не превышают 1°- 3°, а базис фотографирования практически горизонтален, воспользуемся формулами связи координат точек местности и координат их изображений на стереопаре снимков идеального случая съемки ( 2.4):
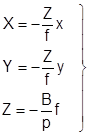 . ( 2.4)
. ( 2.4)
Сначала получим среднюю квадратическую ошибку определения высоты точки Z местности. Для этого продифференцируем третью формулу выражения (1.8.4) по аргументу р.
![]() .
.
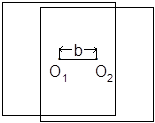 |
Заменим величину р на b – базис в масштабе снимка.
Рис.1
На рис.1 О1 и О2 – главные точки снимка.
В результате получим
![]() .
.
Перейдя к средним квадратическим ошибкам получим формулу:
![]() . ( 1)
. ( 1)
Для получения средних квадратических ошибок определения координат Х и Y точки местности продифференцируем первые две формулы выражения (1.8.4) по аргументам x, y, Z и перейдем к средним квадратическим ошибкам.
В результате получим
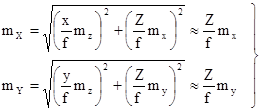 . ( 2)
. ( 2)
В качестве примера вычислим величины mX , mY и mZ точек местности, определенных по стереопаре снимков масштаба 1:5000, полученной АФА с f =150 мм и форматом кадра 23х23 см, с продольным перекрытием 60%.
Будем считать, что на стереопаре снимков точки были измерены с ошибками
![]() .
.
В этом случае высота фотографирования
![]() ;
;
а базис фотографирования в масштабе снимка
![]() .
.
Средние квадратические ошибки определения координат точки местности, вычисленные по формулам ( 1) и ( 2) будут равны:
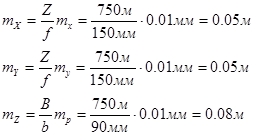 .
.
29-04-2015, 00:34
