Министерство образования Российской Федерации
Федеральное агенство по образованию
Государственное образовательное учреждение
Высшего профессионального образования
Кафедра фотограмметрии и дистанционного зондирования
Курсовая работа по дисциплине “Автоматизированная обработка аэрокосмической информации”
на тему:
“Цифровая фототриангуляция для создания топографических карт”
Выполнил:
Ст. гр. ИП-41
Пашинский В.А.
Проверил:
Широкова Т.А
Новосибирск, 2008г
Содержание
Введение
1. Цифровая фототриангуляция
1.1 Сущность, классификация и назначение фототриангуляции
1.2 Достоинства цифровой фототриангуляции
1.3 Сущность основных методов цифровой и аналитической фототриангуляции
1.3.1 Метод независимых моделей
1.3.2 Построение блочных сетей фототриангуляции методом связок
1.3.3 Построение блочной сети фототриангуляции объединением одиночных моделей
1.3.4 Построение блочной сети фототриангуляции объединением независимых маршрутных моделей
1.4 Особенности цифровой фототриангуляции
2. Технология построения блочной сети фототриангуляции на ЦФС «Фотомод»
2.1 Краткая характеристика ЦФС «Фотомод»
2.2 Основные процессы технологии построения блочной сети фототриангуляции на ЦФС «Фотомод»
3. Построение блочной сети фототриангуляции на ЦФС «Фотомод»
3.1 Оценка фотографического и фотограмметрического качества исходных фотоматериалов
3.2 Составление рабочего проекта построения блочной сети ПФТ
3.3 Подготовка исходных данных для построения сети
3.4 Ввод параметров проекта
3.5 Внутреннее ориентирование снимков
3.6 Построение и уравнивание блочной сети фототриангуляции
3.7Оценка точности, контроль качества и анализ результатов цифровой фототриангуляции
4. Исследования точности построения блочной сети фототриангуляции с использование ЦФС «Фотомод»
Заключение
Список использованных источников
Введение
В настоящее время во всех фирмах, занимающихся фотограмметрической обработкой снимков, применяется цифровой способ фототриангуляции и соответствующие программные продукты. Поэтому целью данной курсовой работы является изучение теоретических основ и получение практических навыков построения сетей пространственной фототриангуляции по результатам аэрофотосъемки с использование программного продукта.
В данной курсовой работе в первом разделе будут рассмотрены понятие пространственной цифровой фототриангуляции, назначение, достоинства, основные методы, а также её особенности.
Во втором разделе будет рассмотрена краткая характеристика ЦФС «Фотомод» и технология построения блочной сети фототриангуляции на ЦФС «Фотомод».
В третьем разделе будет подробно рассмотрено построение блочной сети фототриангуляции на ЦФС «Фотомод», включающее оценку фотографического и фотограмметрического качества исходных материалов, составление рабочего проекта, подготовку исходных данных для построения сети, внутреннее ориентирование снимков, измерение плоских координат опорных, межмаршруных и связующих точек снимков, построение и уравнивание блочной сети фототриангуляции, оценку точности, контроль качества и анализ результатов цифровой фототриангуляции.
В четвертом разделе будут приведены результаты исследования точности построения блочной сети фототриангуляции и проведён анализ результатов.
1.Цифровая фототриангуляция
1.1 Сущность, классификация и назначение фототриангуляции
Сущность фототриангуляции заключается в построении модели местности по снимках, принадлежащим одному или нескольким маршрутам, и внешнем ориентировании этой модели. Фототриангуляция позволяет определять по снимкам плановое положение и высоты опорных точек, необходимых для создания фотопланов, ортофотопланов, карт, цифровой модели рельефа (ЦМР), цифровой модели местности (ЦММ). Также позволяет определять элементы внешнего ориентирования снимков. Основная цель пространственной фототриангуляции (ПФТ) – максимально сократить трудоёмкие полевые геодезические работы, заменить их на камеральные.
ПФТ можно классифицировать[6]:
1) по количеству маршрутов:
- одномаршрутная, которая строится по снимкам, принадлежащим одному маршруту;
- многомаршрутная, или блочная, которая строится по снимкам, принадлежащим двум и более маршрутам;
2) по технологии построения сети фототриангуляции:
- аналоговая, основанная на использование универсальных приборов;
- аналитическая,основанная на применении высокоточных автоматизированных стереокомпараторов и ЭВМ;
- цифровая, при которой используются цифровые изображения;
3) в зависимости от использования физических измерений:
- с использованием физических измерений;
- без использования физических измерений;
4) по назначению:
- каркасная, развивающаяся перпендикулярно к направлению заполняющих маршрутов с целью обеспечения опорными точками, необходимыми для фототриангуляции по заполняющим маршрутам;
- заполняющая, обеспечивающая опорными точками каждую стереопару.
Различают 3 способа одномаршрутной ПФТ:
1) метод независимых моделей;
2) метод частично зависимых моделей;
3) метод связок.
Различают 3 способа многомаршрутной ПФТ:
1) способ связок;
2) способ независимых моделей;
3) способ независимых маршрутов.
1.2 Достоинства цифровой фототриангуляции
Цифровая фототриангуляция имеет следующие достоинства[6]:
1) высокая степень автоматизации;
2) высокая точность благодаря:
- возможности учёта геометрических искажений в координатах точек снимков;
- возможности обработки избыточных измерений;
- использованию мощных компьютеров;
- использованию строгих алгоритмов обработки снимков;
3) возможность обработки снимков различного формата с различными элементами внутреннего и внешнего ориентирования снимков, снимков, полученных различными съемочными системами;
4) широкие функциональные возможности;
5) решена проблема старения материала;
6) возможность улучшения изобразительного качества снимков;
7) высокая производительность труда и культура производства;
8) нет необходимости в сложном обслуживании.
1.3 Сущность основных методов цифровой и аналитической фототриангуляции
1.3.1 Маршрутная фототриангуляция методом независимых моделей
Основные этапы построения ПФТ методом независимых моделей[2]:
1) предварительная обработка результатов измерений координат точек снимков. Осуществляется переход от отсчётов, полученных при измерении снимков на приборе, к плоским координатам точек снимков x, y и учет всех систематических ошибок в координатах точек снимков (за дисторсию объектива АФА, деформацию фотоматериала, рефракцию световых лучей и др.);
2) взаимное ориентирование снимков.
На данном этапе определяются элементы взаимного ориентирования снимков вбазисной системе (
).
В качестве исходного уравнения используется условие компланарности соответствующих лучей в базисной системе:
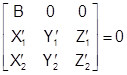, (1.1)
где
- пространственные координаты точек левого и правого снимков. В уравнении (1.1) известными будут
, неизвестными являются элементы взаимного ориентирования.
, (1.2)
где 
- плоские координаты точек снимков;
- направляющие косинусы, являющиеся функциями элементов взаимного ориентирования снимков;
- элементы внутреннего ориентирования снимков.
На основе (1.1) получим уравнение вида
(1.3)
Уравнение (1.3) не линейны по отношению к элементам взаимного ориентирования снимков. Их решают итерационным методом, предварирительно приведя их к линейному виду разложением в ряд Тейлора, ограничиваясь производными первого порядка малости;
3)определение фотограмметрических координат точек одиночных моделей. Выполняется по формулам прямой фотограмметрической засечки:
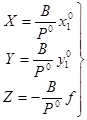(1.4)
, (1.5)
где 
– трансформированные координаты точек левого снимка,
– трансформированный продольный параллакс.
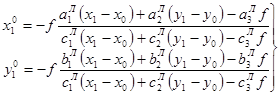. (1.6)
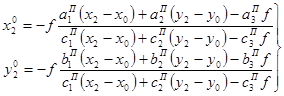. (1.7)
4) подсоединение независимых моделей.
На данном этапе перевычисляются координаты точек в единую систему координат всей сети. Обычно в качестве системы координат маршрутной сети принимают фотограмметрическую систему координат первой модели маршрута. Для подсоединения моделей используются координаты связующих точек.
В качестве исходного принимается уравнение связи координат точек последующей модели с предыдущей:
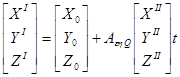, (1.8)
где 
- координаты точек в системе координат маршрутной модели (сети); 
-координаты этих же точек в системе координат последующей модели;
- матрица направляющих косинусов, вычисленных через углы 
;
t-масштабный коэффициент;
- координаты начала системы координат последующей модели в системе координат маршрутной сети.
Этап подсоединения модели состоит из двух процессов. Сначала вычисляются
, а известными будут
.
Затем вычисляются координаты точек присоединяемой модели в системе координат маршрутной сети. Известными будути координаты
точек модели, полученные по формулам(1.4). По формулам(1.9)вычисляются координатыприсоединяемой модели в системе координат маршрутной сети.
5) внешнее ориентирование сети.
На данном этапе перевычисляются координаты точек сети в заданную внешнюю систему координат.Необходимо минимум три опорных точки.
Для внешнего ориентирования сети используются координатыX, Y, Zопорных точек и уравнения вида:
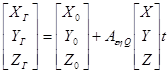. (1.9)
где 
координаты начала системы координат сети;
фотограмметрические координаты точек сети;
геодезические координаты точек местности.
В начале известны координаты опорных точек в геодезической системе и фотограмметрические координаты этих точек, полученные из уравнивания сети. В качестве неизвестных выступают 7 элементов ориентирования геодезической сети:
.
Определив 7 этих неизвестных, будут определяться геодезические координаты 
всех точек сети ПФТ.
6) исключение деформации сети.
Деформацию сети ПФТ можно описать различными полиномами.
Например, обобщённого типа:
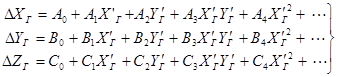, (1.10)
где
– это коэффициенты деформации,
– геодезические координаты точек сети, полученные на этапе 5 из геодезически ориентированной сети.
Из-за деформации сети после ее геодезического ориентирования на опорных точках будут получены расхождения координат :
(1.11)
Исключение деформации сети состоит из 2 процессов: сначала будут известны, 
опорных точек, неизвестными будут коэффициенты
, а исходными для определения коэффициентов будут уравнения(1.10).
После определения коэффициентов деформации вычисляется величина разностикоординат
характеризующие деформацию сети для всех точек сети по формулам (1.10).
Затем вычисляются исправленные координаты точек сети:
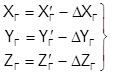. (1.12)
1.3.2 Построение блочных сетей фототриангуляции методом связок
Наиболее строгим методом построения блочных сетей пространственной фототриангуляции аналитическим и цифровым способами по сравнению с методом независимых моделей является метод связок[2]. В основе метода связок лежат уравнения коллинеарности проектирующих лучей:
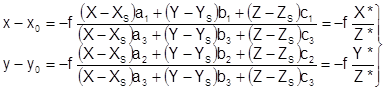, (1.13)
В уравнении будут известны f, x0
, y0
,x, y. Неизвестны элементы внешнегоориентирования снимков
, также X, Y, Z – координаты точек сети ПФТ.
Уравнения (1.13) нелинейные и решаются итерационным методом.
На основе (1.13) имеем уравнение поправок вида:
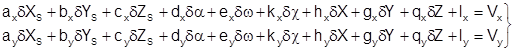, (1.14)
Уравнения (1.14) решаются по методу наименьших квадратов.
lx и ly – свободные члены, вычисляемые по формулам:
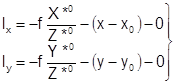, (1.15) где 
– вычисляются по формулам (1.13) подстановкой в нихприближённых значений неизвестных
.
Достоинством метода связок является то, что сеть строится и уравнивается одновременно для всех точек, входящих в блок, а также поправки находятся непосредственно к измеренным величинам, что обеспечивает более высокую точность построения сети. Недостатками этого метода являются: сложность задания приближённых значений неизвестных (для решения этой проблемы можно предварительно уровнять сеть менее строгим методом, а её результаты использовать в качестве приближённых значений), должны отсутствовать грубые ошибки, должны быть исключены систематические ошибки (или сведены к минимуму).
1.3.3 Построение блочной сети фототриангуляции объединением одиночных моделей
Этот метод основан на том[2], что сначала по каждой стереопаре, входящей в блок, строятся независимые одиночные модели, каждая из которых имеет свой масштаб и свою систему координат.
В процессе уравнивания моделей в блоке, все независимые модели приводятся к определенному масштабу и в единую пространственную систему координат на основе совместного внешнего ориентирования моделей.
Исходным является уравнение:
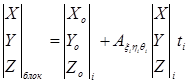, (1.16)
где i – номер модели,
- элементы внешнего ориентирования для каждой модели. Исходными данными для формирования блока из независимых моделей служат
, 
и
. Используются условия равенства 0:
- разностейкоординат опорных точек, полученных из фототриангуляции и из полевых геодезических работ:
- уклоненийкоординат центров проектирования, полученных из ПФТ и зафиксированных в полете с помощью бортовых приборов;
- расхожденийкоординат связующих и общемаршрутных точек, лежащих в зоне поперечного перекрытия снимков соседних маршрутов.
Эти уравнения будут составляться для опорных точек и центров фотографирования.
Для связующих точек, расположенных в зоне тройного продольного перекрытия снимков и общемаршрутных точек, расположенных в зоне поперечного перекрытия снимков будут составляться уравнения вида:
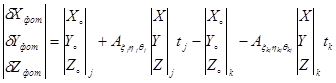(1.17)
Уравнения (1.16) и (1.17) решаются совместно. В результате решения определяются: , по которым далее по формулам (1.16) определяются координаты X, Y, Z в системе координат блочной сети.
Достоинством этого метода является то, что он проще в реализации, а недостатком – он менее строг с точки зрения уравнивания, чем метод связок.
1.3.4 Построение блочной сети фототриангуляции объединением независимых маршрутных моделей
Сущность данного метод заключается в том[2], что объединяются независимые маршрутные сети (построенные допустим методом независимых и частично зависимых моделей). Маршрутные сети предварительно внешне ориентированы в единой пространственной прямоугольной системе координат блока. В основе объединения маршрутных сетей в единый фототриангуляционный блок используется равенство нулю: 1) разности геодезических координат полученных из геодезии и ПФТ δгеод; 2) уклонений координат центров фотографирования, полученных из фототриангуляции и зафиксированных в полёте с помощью бортовых приборов δборт;
3) расхождений координат общемаршрутных точек δфот.
Исходными данными для объединения маршрутных сетей в единый блок служат, и .
Уравнивание маршрутных сетей в блоке выполняется одновременно с исключением деформации сетей ПФТ.
, (1.18)
где i – номер маршрутной модели,
Ci – коэффициенты, характеризующие деформацию фототриангуляционной маршрутной сети.
, (1.19)
где Ri – систематическая погрешность показаний бортовых навигационных приборов;
(1.20)
Уравнения (1.19) – (1.20) решаются совместно, из которых определяются неизвестные Ci и Ri .
На втором этапе для всех точек маршрутных сетей вычисляются велечины поправок
(1.21)
Вид функции (1.21) определяется типом выбранных для уравнивания полиномов
.После вычисления
можно найти исправленные координаты точек сети:
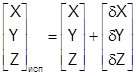(1.22)
Достоинством данного метода является то, что он проще в реализации, легче выявлять грубые ошибки в координатах общемаршрутных точек, а также результаты ПФТ по данному методу можно использовать в качестве приближённых значений неизвестных. Недостаток жёсткие требования к расположению опорных точек и их числу, также уравниваются функции от измеренных величин, а не сами измеряемые величины.
1.4 Особенности цифровой фототриангуляции
Пирамиды изображений для хранения цифровых изображений.
При обработке цифровых изображений[7] при ПФТ часто возникает необходимость просмотра снимков в уменьшенном масштабе. Для этих целей в программах ПФТ посчитанные один раз изображения уменьшенного масштаба, записываются и хранятся на диске во время всего сеанса обработки в виде «пирамид изображений». В этом случае информационное поле описывается упорядоченным набором изображений, располагаемых одно над другим.
Для формирования пирамиды изображений исходный цифровой снимок разбивается на блоки (обычно 2 х 2 пикселя). Для каждого блока вычисляется среднее арифметическое значение яркости, которое и будет присвоено пикселю для данного блока на следующем уровне пирамиды. Эта процедура повторяется необходимое число раз. Каждое последующее изображение пирамиды будет иметь разрешение в 2 раза меньше предыдущего, а занимаемый объём памяти соответственно в 4 раза
Хранение пирамид изображений оправдано, так как увеличевает скорость обработки.
Тайловая структура организации данных цифровых изображений.
В качестве модели организации данных цифровых изображений[7] используется тайловая структура, которая заключается в следующем:
Исходное изображение делится на блоки (тайлы), размер которых фиксирован.
При необходимости обработки конкретного участка изображения осуществляется перемещение на данный адрес и считывается нужный файл. Эта организация данных позволяет быстро считывать с диска и отображать на экране отдельные участки изображения.
Реляционная модель организации данных.
Для обеспечения гибкости сбора данных и хранения результатов измерения координат точек снимков в современных программных продуктах используется реляционная модель данных[7].
| Таблица 1 «Сведения о точках сети» | Таблица 2 «Сведения о снимках» |
| Номер точки | Идентификатор снимка |
 X,Y,Z |
 Элементы внешнего ориентирования снимка |
| Описание точки | Другие параметры |
| Таблица 3 «Сведения о точках снимка» |
| Номер точки |
| Идентификатор снимка |
| Измеренные х,у |
| Другие параметры |
Таблица 1 служит для хранения номеров и координат опорных, контрольных и связующих точек (номера точек не должны повторяться).
Таблица 2 служит для хранения информации о снимках, используемых в обработке. В качестве данных выступают идентификатор снимка, элементы внешнего ориентирования, результаты внутреннего ориентирования снимка и т.п.
В таблице 3 хранятся непосредственно измеренные координаты точек снимков х,у. Каждому измерению х,у в этой таблице соответствует номер измеряемой точки и идентификатор снимка, на котором производилось измерение.
Такая организация данных позволяет однозначно сопоставить каждому измерению соответствующую точку местности (сети) и снимок, на котором выполнено измерение. Она позволяет хранить «бесконечное» число опорных, контрольных, связующих точек и результатов измерения их координат.
Алгоритмы автоматического отождествления соответственных точек снимков.
Ключевым алгоритмом автоматизации фотограмметрических измерений является поиск соответственных точек на паре снимков[7].
В соответствии с методами представления видеоинформации все множество алгоритмов отождествления можно разделить на три класса:
- алгоритмы площадного сопоставления (ABM), основанные на сравнении двумерных функций изображений;
- алгоритмы, базирующиеся на сопоставлении структурных описаний (FBM);
- алгоритмы, в основе которых лежит разложение функции изображения по некоторому базису.
Рассмотрим подробнее первую группу. Здесь в качестве примитивов (элементов описаний), участвующих при сопоставлении двух изображений служат пиксели. Точность этих алгоритмов составляет от 0,1 до 0,2 размера пикселя. Они чувствительны к изменению радиометрических и геометрических свойств изображения, требуют больших вычислительных затрат и характеризуются большой вероятностью грубой ошибки в областях расположения высотных объектов и плохих или повторяющихся структур. Примерами площадных алгоритмов являются алгоритм взаимной корреляции и метод наименьших квадратов. Критерием подобия для этих алгоритмов соответственно служат коэффициент взаимной корреляции и сумма квадратов разностей
29-04-2015, 00:52