Таблиця 2 Повне та безповоротне витрачання води в різних галузях народного господарства України
| Галузь | Витрачення води в % від загального, що споживається галуззю | |
| повне | безповоротне | |
| Промисловість | 45 | 16 |
| Сільське господарство | 39 | 76 |
| Комунальне господарство | 16 | 8 |
Таким чином, безповоротне водоспоживання є найбільшим в сільському господарстві, де вода витрачається на випаровування з полів зрощення і на інфільтрацію з каналів.
Аналіз стану водних ресурсів в Україні показує, що при збереженні існуючого технологічного рівня в промисловості і в сільському господарстві водний дефіцит може охоплювати практично всі річки. Це свідчить про те, що в найближчому майбутньому головним лімітуючим чинником у розвитку продуктивних сил України виступатиме водний. Тому завдання керівних водогосподарських органів полягає в раціональному використанні і охороні водних ресурсів, жорсткій економії води, широкому впровадженні водооборотних систем, маломістких технологіях.
В першу чергу воду треба давати населенню, тваринництву і працюючим галузям народного господарства. Залишок водних ресурсів потрібно так розподілити, щоб вода могла принести найбільший економічний ефект за рахунок розвитку відповідної галузі. Наприклад, в післявоєнні п’ятирічки річний стік використовувався для вироблення електроенергії, в 1970–1990 роках значна кількість його ішла на зрощення сільськогосподарських культур, в даний час пріоритетним напрямком використання води є або промисловість, або рибне, або сільське господарство.
3. Дати визначення «забезпеченість стоку». Визначення річного стоку розрахункової забезпеченості
Стік змінюється як в просторі, так і в часі. В часі він змінюється як протягом року, що було розглянуто в 4-му розділі, так і в багатолітті. Тому в даному розділі буде розглянуто багаторічне коливання поверхневого стоку.
перша причина мінливості це – залежність стоку від метеочинників (опадів, температури та інших), які самі змінюються в часі.
Друга причина – в його формуванні. Ця причина дуже багатофакторна. Це і стан поверхні землі (тала або мерзла, розорена або нерозорена), рівень вологозапасів у ґрунті, кількість води у водних джерелах.
Третя причина – сонячна активність.
Таким чином, сукупність цих чинників формують величини стоку, які є випадковими величинами. А випадкові величини вивчають за теорією ймовірностей. Тому виникає необхідність в ознайомленні з деякими поняттями теорії ймовірностей. Наприклад, випадкова подія. Це така подія, яка при наявності відповідного комплексу умов може наступити, а може і не наступити. Випадкові події формуються великим комплексом чинників, які не можливо не спрогнозувати і не прорахувати.
Кількісно випадкові події можуть бути виражені у випадкових величинах. Однак, в деяких випадках ці величини можуть бути випадковими і невипадковими. Наприклад, протягом року в річці один раз спостерігається найбільша витрата води. Ця максимальна величина обов’язково повинна бути. Тому вона не випадкова. Але, якщо взяти всі максимальні величини за ряд років, то в цьому ряді ця величина випадкова.
В той же час випадкові гідрологічні величини підлягають деяким закономірностям. Наприклад, циклічності, коли протягом ряду років спостерігаються мінімальні витрати в річках, а потім, навпаки – максимальні.
Сукупність випадкових величин називається статистичним рядом. В свою чергу, статистичний ряд характеризує зміну випадкових величин у часі. Гідрологічні ряди, в основному, є статистичними рядами.
Кожний гідрологічний ряд характеризується такими параметрами:
1. Середня арифметична величина ![]() ;
;
2. Коефіцієнт варіації Сv ;
3. Коефіцієнт асиметрії Сs .
Візьмемо для прикладу ряд гідрологічних величин і розглянемо його характеристики. Припустимо, є дані середньорічних витрат за “n” років. Позначимо витрати за кожен рік через X1 ;X2 ;…Xn
Для визначення інших характеристик ряду спочатку обчислюють ступінь розкидання ряду, тобто мінливості його, який можна одержати через різницю між будь-якими і-м значенням і середнім ![]() , тобто
, тобто
![]()
Однак, для характеристики ряду важливо знати середнє відхилення, тому що окремі відхилення не дають повного уявлення про розкидання точок біля середини.
Оскільки відхилення мають різні знаки, то сума їх дорівнює нулю і середнє значення ![]() також дорівнює нулю. Тому
також дорівнює нулю. Тому ![]() не може бути характеристикою ряду.Щоб позбутись від впливу знаків при відхиленнях, усі відхилення підносять до квадрату, а суму квадратів усіх відхилень ділять на число членів ряду. З цього виразу добувають корінь квадратний. Одержана величина
не може бути характеристикою ряду.Щоб позбутись від впливу знаків при відхиленнях, усі відхилення підносять до квадрату, а суму квадратів усіх відхилень ділять на число членів ряду. З цього виразу добувають корінь квадратний. Одержана величина ![]() називається середнім квадратичним відхиленням і визначається за формулою:
називається середнім квадратичним відхиленням і визначається за формулою:
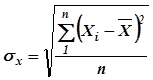
Якщо число членів ряду ![]() менше ніж 30, середнє квадратичне відхилення треба визначати за формулою:
менше ніж 30, середнє квадратичне відхилення треба визначати за формулою:
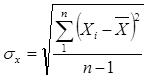
Середнє квадратичне відхилення – абсолютна характеристика мінливості даного ряду.
Для порівняння мінливості з іншими статистичними рядами необхідно виразити величину ![]() в частках від
в частках від ![]() . Одержане значення називається коефіцієнтом варіації і визначається за формулою:
. Одержане значення називається коефіцієнтом варіації і визначається за формулою:

Для зручності і спрощення гідрологічних розрахунків статистичні ряди дуже часто виражають не в абсолютних величинах, а у відносних, тобто, застосовують безрозмірні ряди. Для цього кожний член розмірного ряду ділять на середнє арифметичне значення, одержуючи величини, які називаються модульними коефіцієнтами ![]()
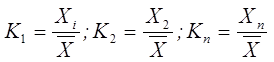
Безрозмірний ряд має дві основні властивості:
1. Сума членів безрозмірного ряду дорівнює числу членів ряду
(![]() )
)
2. Середнє арифметичне значення безрозмірного ряду дорівнює одиниці
(![]() )
)
При заміні в формулах (40 і 41) величини ![]() на
на ![]() одержують значення коефіцієнта варіації для безрозмірного ряду
одержують значення коефіцієнта варіації для безрозмірного ряду
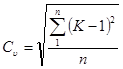 і
і 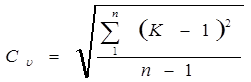
Третьою характеристикою статистичного ряду є коефіцієнт асиметрії (![]() ). Ряд називається симетричним, якщо додатні і від’ємні відхилення членів ряду повторюються однаково часто. Якщо цього немає, з’являється асиметричність ряду, що характеризується коефіцієнтом
). Ряд називається симетричним, якщо додатні і від’ємні відхилення членів ряду повторюються однаково часто. Якщо цього немає, з’являється асиметричність ряду, що характеризується коефіцієнтом ![]() . Для розмірного ряду
. Для розмірного ряду ![]() визначається так:
визначається так:
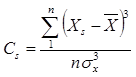
а для безрозмірного
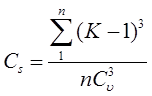
Гістограма і крива розподілу
Наочне уявлення про величини коефіцієнтів ![]() і
і ![]() дають гістограма і крива розподілу величин статистичного ряду. Частіше тут беруть безрозмірні ряди.
дають гістограма і крива розподілу величин статистичного ряду. Частіше тут беруть безрозмірні ряди.
Для побудови гістограми всі значення ряду розміщують в спадному порядку. Потім його розбивають на однакові інтервали і визначають частоту повторювань “n” в кожному інтервалі. Потому, відкладаючи по осі ординат n , а по осі абсцис К, будують гістограму. На рис. 2 і 3 зображені гістограми і крива розподілу.
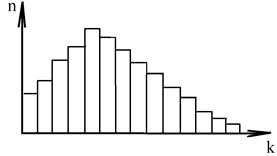
Рис. 2. Гістограма розподілу
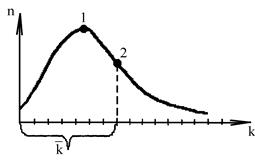
Рис. 3. Крива розподілу
Криву розподілу можна одержати, якщо при будові гістограми зменшувати інтервал до нескінченно малої величини. Однак, при цьому бажано мати і нескінченну кількість членів ряду.
Крива розподілу дає наочне уявлення про закони розподілу випадкової величини. Вона характеризує ймовірність появи того чи іншого значення ряду випадкових величин.
Що таке ймовірність? Імовірність – це міра можливості появи тієї чи іншої події або групи приблизно однакових подій або величин.
Імовірність появи будь-якої події або величини (![]() ) визначається за формулою:
) визначається за формулою:
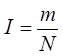
де ![]() – група, а точніше, кількість приблизно однакових подій або величин;
– група, а точніше, кількість приблизно однакових подій або величин;
![]() – загальна кількість всіх можливих випадків подій або величин.
– загальна кількість всіх можливих випадків подій або величин.
Наприклад, маємо дані за середньорічними витратами річки за 100 років, з яких протягом 30 років витрати були в межах 100…70 м3 /с; протягом 50 років – в межах 70…40 м3 /с; протягом 20 років – в межах 40...10 м3 /с. Тоді ймовірність появи витрат від 100 до 70 м3 /с буде
![]()
Імовірність появи витрат від 70 до 40 м3 /с буде
![]()
Імовірність появи витрат від 40 до 10 м3 /с становитиме
![]()
Таким чином імовірність коливається в межах від 0,0 до 1,0. Якщо імовірність події дорівнює нулю, вона абсолютно неможлива, а якщо одиниці то вірогідна.
На кривій розподілу (рис. 3) виділяються декілька характерних точок. Так, точка 1 відповідає максимальній частоті повторювань і називається модою. Точка 2 відповідає середньому значенню ряду і називається центром розподілу.
Криві розподілу бувають симетричні, коли ![]() , і асиметричні, коли
, і асиметричні, коли
![]()
Крива розподілу буде симетричною, коли точки 1 і 2 співпадають. Гідрологічні ряди характеризуються асиметричністю, причому – додатною, бо точка 1 знаходиться праворуч від точки 2.
Величина ординати в центрі кривої характеризує мінливість ряду: чим більша ордината, тим більший коефіцієнт ![]() – і навпаки.
– і навпаки.
Забезпеченість значень гідрологічного ряду
В практиці проектування і будівництва гідротехнічних споруд будівельними нормами і правилами встановлено – кожна споруда залежно від класу капітальності має розраховуватись на певну забезпеченість. Забезпеченість частіше виражається у відсотках. Так зрошувальні системи розраховуються на 75–90%-у, осушувальні – на 10–25%-у, водозабірні споруди водопостачання на 95–97%-у, будинки і греблі ГЕС на 0,01–0,1%-у забезпеченість.
Так що ж таке забезпеченість? Для цього, передусім, треба знати правила її визначення. Відповідно цим правилам усі значення гідрологічного ряду треба розташувати або у зростаючому, або у спадному порядку, пронумерувати їх і за нижчеподаною формулою визначити їх забезпеченість.
![]()
де ![]() – порядковий номер члена ряду у спадному (зростаючому) ряду цифр;
– порядковий номер члена ряду у спадному (зростаючому) ряду цифр;
![]() – кількість членів ряду.
– кількість членів ряду.
Виходячи з того, в якій послідовності розміщені значення ряду, формулювання поняття забезпеченості буде різне:
1. Під забезпеченістю будь-якої величини ряду розуміється імовірність перевищення значення, що розглядається, серед сукупності всіх можливих значень.
2. Під забезпеченістю будь-якої величини ряду розуміється імовірність перевищення значення, що розглядається, і більше нього, серед сукупності всіх можливих значень.
Перше формулювання придатне для зростаючого ряду, друге – для спадного. В інженерній гідрології прийнято розміщувати значення за другою схемою.
Призначення і будова кривих забезпеченності
Криві забезпеченості частіше будують для безрозмірних рядів, в яких усі значення виражені в модульних коефіцієнтах ![]() . Кожне забезпечене значення ряду має свій модульний коефіцієнт, який визначається, наприклад, для витрат 10%-ої забезпеченості як:
. Кожне забезпечене значення ряду має свій модульний коефіцієнт, який визначається, наприклад, для витрат 10%-ої забезпеченості як:
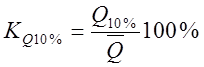
Дуже часто при розрахунках розмірів гідротехнічних споруд на пропуск екстремальних величин стоку забезпеченістю менше 5% або більше 95%, коли такі величини не спостерігались, але є середні значення ряду, то їх можна визначити, якщо знати ![]() відповідної забезпеченості, тобто:
відповідної забезпеченості, тобто:
![]()
Для цього будуються криві забезпеченості. Є декілька способів їх побудови. Критерієм вибору, частіше, є достатність даних спостережень за стоками в будь-якому створі річки.
Будова кривої забезпеченості при достатній кількості даних
Першим прийомом побудови кривої забезпеченості при достатній кількості даних спостережень (N®100) є перебудова гістограми розподілу. Для цього по осі ординат відкладають модульний коефіцієнт ![]() , а по осі абсцис частоту повторювань
, а по осі абсцис частоту повторювань ![]() (рис. 4).
(рис. 4).
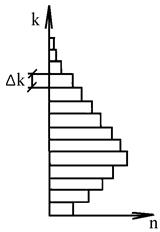
Рис.4. Гістограма
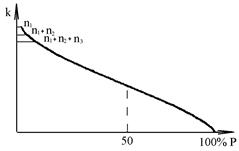
Рис. 5. Крива забезпеченості
Починаючи з найбільших членів ряду послідовно підсумовують частоти повторювань в кожному інтервалі ![]() і відкладають по осі ординат значення
і відкладають по осі ординат значення ![]() , а по осі абсцис або
, а по осі абсцис або ![]() , або їх вираз у відсотках, тобто
, або їх вираз у відсотках, тобто ![]() . Одержані точки з’єднують плавною кривою, яка і є кривою забезпеченості (рис. 5). Задаючись розрахунковою забезпеченістю, відкладають її значення на осі абсцис, одержують точку, через яку проводять пряму до перетину з кривою і далі до осі ординат. Таким чином знаходять
. Одержані точки з’єднують плавною кривою, яка і є кривою забезпеченості (рис. 5). Задаючись розрахунковою забезпеченістю, відкладають її значення на осі абсцис, одержують точку, через яку проводять пряму до перетину з кривою і далі до осі ординат. Таким чином знаходять ![]() потрібної забезпеченості.
потрібної забезпеченості.
Другий спосіб побудови кривої забезпеченості при достатній кількості даних це – використання формули, за допомогою якої знаходять забезпеченість кожного члена безрозмірного ряду. Виносячи ![]() і
і ![]() на графік, одержують також ряд точок, з’єднання яких дає криву забезпеченості.
на графік, одержують також ряд точок, з’єднання яких дає криву забезпеченості.
Аналогічно криву розподілу можна перебудувати в криву забезпеченості.
Будова кривої забезпеченості при недостатності даних спостережень
Частіше є дані за короткий відрізок часу (20–25 років). При будові емпіричної кривої забезпеченості на її кінцях залишаються ділянки, де неможливо встановити положення кривої із-за відсутності необхідних даних. А це дуже важливі значення ![]() , бо за їх допомогою визначаються екстремальні значення стоку. В таких випадках користуються значеннями
, бо за їх допомогою визначаються екстремальні значення стоку. В таких випадках користуються значеннями ![]() , що знімають з теоретичних кривих забезпеченості, які побудовані шляхом перебудови кривих розподілу. Криві розподілу можуть мати аналітичний, тобто, теоретичний вираз у вигляді формул. З теоретичних кривих в гідрології найбільш розповсюджені біномальна крива розподілу (відома, як крива Пірсона ІІІ типу) і крива трипараметричного гамма-розподілу, яка була розроблена С. Н. Кріцьким і М. Ф. Менкелем.
, що знімають з теоретичних кривих забезпеченості, які побудовані шляхом перебудови кривих розподілу. Криві розподілу можуть мати аналітичний, тобто, теоретичний вираз у вигляді формул. З теоретичних кривих в гідрології найбільш розповсюджені біномальна крива розподілу (відома, як крива Пірсона ІІІ типу) і крива трипараметричного гамма-розподілу, яка була розроблена С. Н. Кріцьким і М. Ф. Менкелем.
Після інтегрування асиметричної кривої розподілу С. І. Рибкін перебудував її в теоритичну криву забезпеченості і склав таблицю відхилень ординат кривої забезпеченості від середнього значення, при коефіцієнті варіації ![]() і
і ![]() залежно від різних значень
залежно від різних значень ![]() .
.
За допомогою цих таблиць знаходять відхилення, які називаються числами Фостера (![]() ) і затим визначають модульні коефіцієнти за формулою:
) і затим визначають модульні коефіцієнти за формулою:
![]()
Якщо ![]() , то
, то ![]() завжди дорівнює 1, а якщо
завжди дорівнює 1, а якщо ![]() , то і
, то і ![]() .
.
Для визначення ![]() за таблицями потрібно знати
за таблицями потрібно знати ![]() , а для –
, а для – ![]() потрібне
потрібне ![]() . Їх значення визначають за коротким рядом з допомогою формул. Іноді
. Їх значення визначають за коротким рядом з допомогою формул. Іноді ![]() приймається рівною
приймається рівною ![]() .
.
В таблицях трипараметричного гамма-розподілу наведені ординати кривої забезпеченості зразу ж в модульних коефіцієнтах і для визначення розрахункових величин стоку достатньо лише помножити значення ординат на середню величину витрат, тобто
![]()
Повторюваність
Із забезпеченістю має тісний зв’язок повторюваність. Повторюваність – це кількість років, протягом яких величина, що розглядається, з’являється в середньому один раз.
Повторюваність ![]() зв’язана із забезпеченістю
зв’язана із забезпеченістю ![]() такими залежностями:
такими залежностями:
при ![]()
![]()
при ![]()
![]()
Однак, спрогнозувати появу року певної забезпеченості неможливо і, наприклад, при забезпеченості ![]() річний стік може відбуватись в цьому році або через 1000 років.
річний стік може відбуватись в цьому році або через 1000 років.
Розрахункова робота
Варіант 1. Річка Тетерів
Завдання 1. Характеристика басейну річки та гідрографічної мережі
За звітний період було обстежено від витоку до гирла 6 основних річок області: Тетерів, Случ, Уж, Норинь, Ірша, Гнилоп’ять, а також гирло річки Гуйва, три річки в прикордонних з Київською областю створах : р. Кам’янка, р. Ірпінь та р. Роставиця (басейн р. Рось), і р. Уборть яка є транскордонною між Україною та республікою Білорусь .
Відбір проб здійснюється згідно "Програми моніторингу поверхневих вод суші", розробленої Держуправлінням екології та природних ресурсів в Житомирській області. "Програма..." нараховує 18 пунктів, 23 створи на 11 річках з щоквартальним відбором проб в кожному створі (94 проби). Відібрано по "Програмі моніторингу" 94 проб.
Під час інспекційних перевірок діяльності об"єктів-забруднювачів було перевірено також 30 малих річок (Добринка, Глибочок, Бистріївка, Пустоха, Лісна, Лемня, Настя, Церем, Іршиця, Кам’янка, Чорна Руда, Мика, Тетерівка, Лозниця, Смолка, Хомора, Повчанка, Крошенка, Ужиця, Кропивнянка, Руда, П’яток, Постол, Мурованка, Конявка, Кремна, Унава, Білка, Рихта, Очеретян-ка), 27 кар’єрів, 61 ставок, 9 меліоративних каналів, 6 струмків, 2 свердловини, 3 болота, 1 канава, 2 водосховища, 12 криниць.
Річка ТЕТЕРІВ
Річка Тетерів, права притока р.Дніпро, протяжність на території області 247 км. Протікає по території чотирьох районів: Чуднівського, Житомирського, Коростишівського, Радомишльського. Кількість контрольних створів - 27, з них згідно до "Програми..." - 7. Відбір проб проведений 4 рази на рік по кожному створу. Результати представлені у порівнянні з 2004 роком (за середніми значеннями).
У верхньому створі річки 1 км вище смт. Чуднів (с. Волосівка) порівняно з попереднім 2004р спостерігається збільшення вмісту магнію, з 18,5 мг/дм3
в 2004 році до 28мг/дм3
– в 2005, амонію сольового з 0,77 мг/дм3
до 0,95 мг/дм3
заліза загального з 0,32 до 0,49мг/дм3
. Спостерігається незначне зменшення вмісту сульфатів та хлоридів. Решта показників якості води в цьому створі суттєвих змін не зазнали. Показники вмісту важких металів не перевищують рівень ГДК за винятком марганцю,вміст якого перевищує ГДК в 2 рази. Аналізуючи середні значення показників
29-04-2015, 00:34
