В створі 1км нижче смт. Чуднів, (с Дубище) різких змін якості води не cпостерігається. Більшість показників, в порівнянні з минулим роком, істотно не змінилась або має тенденцію до зменшення, за винятком заліза загального вміст якого зріс з 0,37 мг/дм3 до 0,53 мг/дм3 та сольового амонію – з 1,04 до 1,18 мг/дм3 і перевищують норматив ГДК відповідно у 5,3 і 2,4 рази.
Незважаючи на те, що з очисних споруд Чуднівського ПЖКГ скид відсутній (скид відбувається в накопичувач), спостерігається погіршення стану річки в створі 1км нижче смт. Чуднів в порівнянні з верхнім створом.
Оцінюючи стан якості води в створі 5 км вище м. Житомир (водосховище «Відсічне») можна відмітити погіршення значень показників вмісту сольового амонію (з 0,48 мг/дм3 до 0,72 мг/дм3 ) та заліза загального (з 0,22 мг/дм3 до 0,32 мг/дм3 ). Як і в попередньому році є перевищення по марганцю в 2,5 рази ( 0,025 мг/дм3 при нормі ГДК 0,01 мг/дм3 ) . За іншими показниками істо-тних змін не відбулося.
У створі вище гирла річки Кам'янка, показники якості води знаходяться в межах 2004р, лише по вмісту сольового амонію можна відмітити тенденцію до зростання (з 0,74 мг/дм3 до 1,03 мг/дм3 ) . Перевищення норм ГДК є по залізу загальному в 3,1 рази (0,31 мг/дм3 при нормі 0,1 мг/дм3 ), марганцю в 3 рази (0,03 мг/дм3 при нормі 0,01 мг/дм3 ), ХСК і БСК5 , а деякі погіршення в порівнянні із попереднім контрольним створом пояснюється впливом річок Гнило-п’ять та Гуйва .
В створі 0,5 км нижче гирла річки Кам’янка порівняно з 2004р істотних змін не відбулось, за винятком фосфатів, показник яких зріс з 0,48 мг/дм3 до 0,63 мг/дм3 .Перевищення нормативів ГДК має місце по сольовому амонію в2,8 рази ( при нормі 0,5 мг/дм3 -1,42 мг/дм3 ), фосфатах в 3,7 рази (при нормі 0,17 мг/дм3 -0,63 мг/дм3 ), залізу загальному в 3,7 рази (при нормі 0,1 мг/дм3 - 0,37 мг/дм3 ).
У створі нижче міста Житомира, с. Левків, у порівнянні з 2004 роком спостерігається тенденція до зменшення більшості показників якості води, що пов’язане із покращенням роботи ОСК Житомирського ВУВКГ , де була проведена оптимізація технологічного режиму очистки стічних вод. Показники якості зворотних вод значно покращилися і відповідно зменшився вплив скидів ОСК Житомирського ВУВКГ на р. Тетерів. Та все ж, незважаючи на це, у цьому створі має місце перевищення нормативів ГДК по сольовому амонію в 3,3 рази (1,67 мг/дм3 при нормі 0,5 мг/дм3 ), нітритах в 3,6 рази (0,29 мг/дм3 при нормі 0,08 мг/дм3 ), фосфатах в 8,1рази (1,38 мг/дм3 при нормі 0,17 мг/дм3 ), залізу загальному в 3 рази (0,3 мг/дм3 при нормі 0,1 мг/дм3 ), БСК5 в 1,9 рази (5,77 мгО2 /дм3 при нормі 3,0 мгО2 /дм3 ), ХСК в 1,5рази (46,19 мгО2 /дм3 при нормі 30,0 мгО2 /дм3 ), марганцю в 5 разів.
В прикордонному з Київською областю створі, с. Вишевичі, спостерігається незначне коливання середніх значень більшості показників відносно даних 2004 року, лише можна відмітити зростання вмісту фосфатів (з 0,66 мг/дм3 до 0,84 мг/дм3 ) та заліза загального (з0,37 мг/дм3 до 0,46 мг/дм3 ), що у 4,9 та 4,6 відповідно перевищують норму ГДК. Незважаючи на те, що середні значення показників ХСК, БСК5 і сольового амонію протягом 2005 року зменшились, їх значення все ще не досягає значень ГДК.
Гідрохімічний стан річки Тетерів від витоку до прикордонного створу з Київською областю різких змін в порівнянні з минулим роком не зазнав, проте спостерігається незначна тенденція до покращення. Якщо порівнювати якісні показники в першому контрольному створі, 1км вище смт.Чуднів (фоновий створ) і в останньому, прикордонному створі, (с.Вишевичі), то можна відмітити, що за показниками сольового складу і заліза загального майже вдалося досягти фонових значень, а от деякі трофо-сапробіологічні показники зросли: нітрати і нітрити збільшились вдвічі, з 2,8 до 4,4 мг/дм3 і з 0,04 до 0,1 мг/дм3 відповідно, фосфати - майже в четверо з 0,22 до 0,84 мг/дм3 . Причиною погіршення якості води в річці є неефективна робота очисних споруд Коростишівського МКП “Водоканал” , та вплив побутових стоків м.Радомишль.
2. Визначення норми річного стоку при наявності достатньої кількості даних спостережень
Завдання 1 . характеристика басейну річки та гідрографічної мережі
Наводиться гідрографічна характеристика басейну річки.
Довжина lгол головної річки Тетерів становить 247 км, довжина р. Уж – 27 км, р. Случ – 21 км. Річки Уж і Случ є притоками першого порядку.
Площа водозбірного басейну становить 10947 км2 .
Коефіцієнт звивистості kзв визначаємо за формулою:
![]()
Довжина водозбірного басейну L становить 27 км. За формулою визначаємо середню ширину басейну:
![]() км
км
Розраховуємо протяжність річкової системи:
247+27+21=295 км
Коефіцієнт щільності річкової мережі d розраховується за формулою:
d = 295/10947=0,03 км/км2 .
Коефіцієнт нерівномірності розвитку річкової мережі kнер розраховується за формулою:
![]()
Визначити середнє багаторічне значення (норму) річного стоку при наявності даних спостережень.
Дано: середні річні витрати води р. Тетерів за період 1967-2000 рр. (всього за 34 роки).
Розв’язок: розрахунки статистичних параметрів річного стоку проводимо у вигляді таблиці.
У гр. 4 значення річного стоку розташовуємо у порядку зменшення.
Таблиця
| № | Роки | Qi , м3 /с | Qi , м3 /с у ранжованому ряді | ki =Qi /Q0 | ki -1 | (ki -1)2 | (ki -1)3 | lgki | ki *lgki | P=(m/(n+1)) *100% |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 1 | 1967 | 0,81 | 6,53 | 3,023 | 2,023 | 4,0925 | 8,2792 | 0,480 | 1,452 | 2,857 |
| 2 | 1968 | 1,92 | 5,87 | 2,718 | 1,718 | 2,9515 | 5,0707 | 0,434 | 1,180 | 5,714 |
| 3 | 1969 | 2,28 | 3,52 | 1,63 | 0,630 | 0,3969 | 0,2500 | 0,212 | 0,346 | 8,571 |
| 4 | 1970 | 2,29 | 3,49 | 1,616 | 0,616 | 0,3795 | 0,2337 | 0,208 | 0,337 | 11,429 |
| 5 | 1971 | 2,28 | 3,32 | 1,537 | 0,537 | 0,2884 | 0,1549 | 0,187 | 0,287 | 14,286 |
| 6 | 1972 | 1,45 | 3,15 | 1,458 | 0,458 | 0,2098 | 0,0961 | 0,164 | 0,239 | 20 |
| 7 | 1973 | 3,49 | 3,09 | 1,43 | 0,430 | 0,1849 | 0,0795 | 0,155 | 0,222 | 22,857 |
| 8 | 1974 | 0,65 | 3,04 | 1,407 | 0,407 | 0,1656 | 0,0674 | 0,148 | 0,209 | 28,571 |
| 9 | 1975 | 1,65 | 2,43 | 1,125 | 0,125 | 0,0156 | 0,0020 | 0,051 | 0,058 | 31,429 |
| 10 | 1976 | 0,41 | 2,29 | 1,06 | 0,060 | 0,0036 | 0,0002 | 0,025 | 0,027 | 37,143 |
| 11 | 1977 | 3,15 | 2,28 | 1,056 | 0,056 | 0,0031 | 0,0002 | 0,024 | 0,025 | 40 |
| 12 | 1978 | 1,75 | 2,28 | 1,056 | 0,056 | 0,0031 | 0,0002 | 0,024 | 0,025 | 45,714 |
| 13 | 1979 | 3,32 | 2,25 | 1,042 | 0,042 | 0,0018 | 0,0001 | 0,018 | 0,019 | 48,571 |
| 14 | 1980 | 3,09 | 2,22 | 1,028 | 0,028 | 0,0008 | 0,0000 | 0,012 | 0,012 | 51,429 |
| 15 | 1981 | 0,69 | 2,14 | 0,991 | -0,009 | 0,0001 | 0,0000 | -0,004 | -0,004 | 54,286 |
| 16 | 1982 | 0,63 | 2,12 | 0,981 | -0,019 | 0,0004 | 0,0000 | -0,008 | -0,008 | 57,143 |
| 17 | 1983 | 1,08 | 1,98 | 0,917 | -0,083 | 0,0069 | -0,0006 | -0,038 | -0,035 | 60 |
| 18 | 1984 | 1,83 | 1,92 | 0,889 | -0,111 | 0,0123 | -0,0014 | -0,051 | -0,045 | 62,857 |
| 19 | 1985 | 1,52 | 1,83 | 0,847 | -0,153 | 0,0234 | -0,0036 | -0,072 | -0,061 | 65,714 |
| 20 | 1986 | 5,87 | 1,75 | 0,81 | -0,190 | 0,0361 | -0,0069 | -0,092 | -0,074 | 68,571 |
| 21 | 1987 | 6,53 | 1,75 | 0,81 | -0,190 | 0,0361 | -0,0069 | -0,092 | -0,074 | 71,429 |
| 22 | 1988 | 3,52 | 1,65 | 0,764 | -0,236 | 0,0557 | -0,0131 | -0,117 | -0,089 | 74,286 |
| 23 | 1989 | 1,41 | 1,52 | 0,704 | -0,296 | 0,0876 | -0,0259 | -0,152 | -0,107 | 77,143 |
| 24 | 1990 | 1,75 | 1,47 | 0,681 | -0,319 | 0,1018 | -0,0325 | -0,167 | -0,114 | 80 |
| 25 | 1991 | 1,16 | 1,45 | 0,671 | -0,329 | 0,1082 | -0,0356 | -0,173 | -0,116 | 82,857 |
| 26 | 1992 | 1,47 | 1,41 | 0,653 | -0,347 | 0,1204 | -0,0418 | -0,185 | -0,121 | 85,714 |
| 27 | 1993 | 1,38 | 1,38 | 0,639 | -0,361 | 0,1303 | -0,0470 | -0,194 | -0,124 | 88,571 |
| 28 | 1994 | 2,25 | 1,16 | 0,537 | -0,463 | 0,2144 | -0,0993 | -0,270 | -0,145 | 91,429 |
| 29 | 1995 | 2,12 | 1,08 | 0,5 | -0,500 | 0,2500 | -0,1250 | -0,301 | -0,151 | 94,286 |
| 30 | 1996 | 1,98 | 0,81 | 0,375 | -0,625 | 0,3906 | -0,2441 | -0,426 | -0,160 | 97,143 |
| 31 | 1997 | 2,43 | 0,69 | 0,319 | -0,681 | 0,4638 | -0,3158 | -0,496 | -0,158 | 97,234 |
| 32 | 1998 | 2,22 | 0,65 | 0,301 | -0,699 | 0,4886 | -0,3415 | -0,521 | -0,157 | 98,124 |
| 33 | 1999 | 3,04 | 0,63 | 0,292 | -0,708 | 0,5013 | -0,3549 | -0,535 | -0,156 | 98,231 |
| 34 | 2000 | 2,14 | 0,41 | 0,19 | -0,810 | 0,6561 | -0,5314 | -0,721 | -0,137 | 98,654 |
| Сума | 73,56 | 73,56 | 0,000 | 12,3812 | 12,0069 | -2,473 | 2,400 | - | ||
Середню багаторічну величину стоку розраховуємо за формулою:
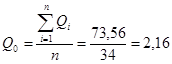 м3
/с
м3
/с
Перевірка розрахунків – сума модульних коефіцієнтів дорівнює кількості років спостережень:
Σki =34,056; Σ(ki -1)=0 (допустима нев’язка – 0,05)
Виразити отриману у вигляді середньої багаторічної витрати води норму стоку через інші характеристики стоку: об’єму, модуль, шар та коефіцієнт стоку.
Дано: норма річного стоку р. Тетерів Q0 =2,16 м3 /с, площа водозбору F=10947 км2 , середньо багаторічна норма річних опадів х0 =20117,7/34=591,7 мм.
Розв'язок: норму стоку виражаємо у інших одиницях стоку за формулами:
W=Q0 *T=2,6*31,56*106 =82,056 млн. м3 (у році 31,56*106 с),
M=Q0 /F*103 =2,16/10947*103 =1,93 л/(с*км2 ),
y=h=W/F*103 =82,056/10947*103 =750 мм
коефіцієнт стоку розраховуємо за формулою:
α=h/x0 =750/591,7=1,3
Визначити коефіцієнт мінливості (варіації) річного стоку.
Дано: дані табл..
Розв'язок:
За методом найбільшої правдоподібності коефіцієнт варіації розраховуємо залежно від статистик λ2 та λ3 :
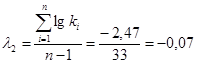
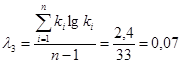
За номограмою знаходимо:
СV =0,6; СS =2СV =2*0,6=1,2.
За методом моментів коефіцієнт варіації обчислюємо за формулою:
![]() .
.
Визначити відносні середні квадратичні похибки норми стоку і коефіцієнта варіації.
Дано:
СV =0,6
Розв'язок: величину відносної середньоквадратичної похибки σQ 0 розраховуємо за формулою:
![]()
Величину відносної середньоквадратичної похибки коефіцієнта варіації δСV визначаємо за формулою:
![]() %
%
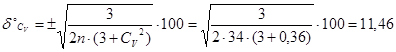 %
%
Завдання 3. Побудова кривих забезпеченості річного стоку
Забезпеченістю гідрологічної характеристики називають імовірність перевищення розглядуваного значення цієї характеристики над усіма можливими її значенями. Наприклад, якщо середньорічна витрата води у 20 м3 /с має забезпеченість 80%, то це означає, що у 80 випадках із 100 спостерігатиметься річна витрата, що дорівнюватиме 20 м3 /с або більше.
Криву забезпеченості, побудовану за даними спостережень, називають емпіричною. Для її побудови хронологічний ряд річних витрат води Q1 , Q2 , Qn систематизують у ранжований ряд (розташовують у порядку зменшення від найбільшого значення до найменшого) і обчислюють забезпеченість Р кожного члена ряду за формулою
![]()
Де m – порядковий номер члена ранжованого ряду; n – кількість членів ряду, тобто кількість років спостережень.
Отримані значення Р наносять на сітківку ймовірностей (тип сітківки залежить від співвідношення СS /СV ) і проводять влавну усереднюючи криву емпіричну криву забезпеченості.
Для згладжування (вирівнювання) та екстраполяції (продовження) емпіричних кривих застосовують теоретичні (аналітичні) криві забезпеченості. Як правило, застосовується аналітична крива три параметричного гама-розподілу при будь-якому співвідношенні СS /СV та біноміальна крива розподілу при СS >2СV .
Для побудови аналітичної кривої три параметричного гама-розподілу ординати її знаходять за таблицею залежно від співвідношення СS /СV ; потім за значенням СV виписують модульні коефіцієнти КР% , які відповідають заданій забезпеченості. Для підвищення точності ординат кривої потрібно враховувати соті частки значення СV (з точністю до двох знаків після коми) шляхом інтерполяції між суміжними колонками цифр.
Ординати біноміальної кривої знаходять за виразом:
КР% =ФР% *СV +1,
Де ФР% - нормоване відхилення ординати кривої забезпеченості від середнього значення (при КР% =1), яке знаходять за таблицею.
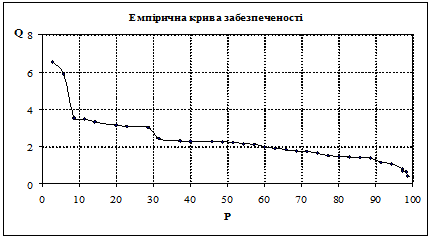
Побудувати емпіричну криву забезпеченості річного стоку.
Дано: середні річні витрати води Qi р.Тетерів за період 1967-1991 рр.
Розвязок: для розрахунку забезпеченості Р значення річного стоку Qi систематизує у ранжований ряд – розташовуємо у порядку зменшення. Координати емпіричної кривої забезпеченості (Р) обчислюємо за формулою:
![]()
Результати обчислень наведено у таблиці, гр..11. за цими даними на сітківку ймовірностей наносимо точки емпіричної кривої. По вісі абсцис відкладаємо забезпеченість (масштаб: 1 см – 5%), по вісі ординат – КР% . Для спрощення графік будуємо на міліметровому папері.
Побудувати теоретичну криву три параметричного гама-розподіу забезпеченості річного стоку.
Дано: коефіцієнт варіації СV =0,6.
Розв'язок: координати теоретичних кривих три параметричного гама розподілу визначаємо за додатком для коефіцієнта асиметрії
СS =1,5СV , СS =2СV , СS =2,5СV
Записуємо їх у таблицю.
Отримані координати теоретичних кривих наносимо на сітківку ймовірностей. Спів ставляючи побудовані теоретичні криві з емпіричною кривою забезпеченості встановлюємо, що крива три параметричного гама розподілу при СS =2,5СV найкраще узгоджується з емпіричною, тому її приймаємо за розрахункову.
Таблиця Координати кривої забезпеченості три параметричного гама-розподілу середньорічних витрат води р. Тетерів
| Забезпеченість | |||||||||||
| Р % | 0,1 | 1 | 5 | 10 | 25 | 50 | 75 | 80 | 95 | 97 | 99 |
| Ординати кривої | |||||||||||
| СS =1,5СV | |||||||||||
| КР% | 3,02 | 2,42 | 1,92 | 1,68 | 1,33 | 0,934 | 0,630 | 0,562 | 0,305 | 0,247 | 0,160 |
| СS =2СV | |||||||||||
| КР% | 3,27 | 2,51 | 1,94 | 1,67 | 1,28 | 0,918 | 0,634 | 0,574 | 0,342 | 0,288 | 0,206 |
| СS =2,5СV | |||||||||||
| КР% | 3,51 | 2,59 | 1,95 | 1,66 | 1,33 | 0,906 | 0,640 | 0,585 | 0,373 | 0,325 | 0,248 |
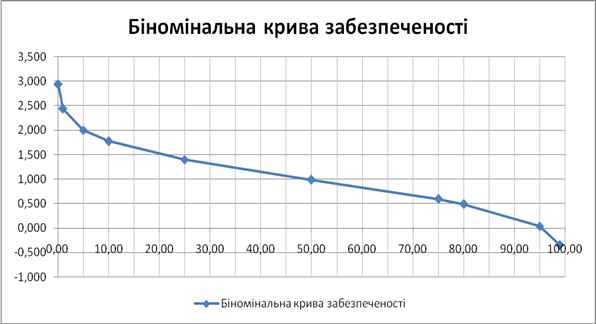
Побудувати біноміальну криву розподілу забезпеченості річного стоку.
Дано: коефіцієнт варіації СV =0,52 коефіцієнт асиметрії СS =2СV =1,2.
Розв'язок: координати біноміальної кривої розподілу знаходимо за виразом КР% =ФР% *СV +1. Розрахунок проводимо у такому порядку: за таблицею додатку 3 знаходимо нормоване відхилення ординати кривої забезпеченості ФР% від середнього значення залежно від СS і обчислюємо значення КР% . результати розрахунків зводимо у тиблицю.
Таблиця
Координати біноміальної кривої забезпеченості річного стоку р. Тетерів
Завдання 4. Розрахунок витрат води заданої забезпеченості
Визначити витрати води забезпеченістю 1, 50 та 80%.
Дано: норма річного стоку р. Тетерів Q0 =2,16 м3 /с, крива забезпеченості три параметричного гама-розподілу при СS =2 СV
Розв'язок: для визначення розрахункових річних витрат води забезпеченістю 1, 50 та 80% з кривої забезпеченості знімаємо значення КР% :
Q1% =2,16*2,51=5,42 м3 /с
Q50% =2,16*0,92=1,99 м3 /с
Q80% =2,16*0,57=1,23 м3 /с
Визначити забезпеченість витрат води 1975 року.
Дано: середньорічна витрата води р. Тетерів у 1975 році Q1975 =1,65 м3 /с, норма річного стоку Q0 =2,16 м3 /с.
Розв'язок: розраховуємо модульний коефіцієнт КР за залежністю:
КР =QP /Q0 =1,65/2,16=0,76, якому за кривою забезпеченості відповідає Р=54%. повторюваність 1 раз на N років розраховуємо за формулою:
N=100/54=2
Тобто, в середньому 1 раз на 2 роки середньорічна витрата води р. Тетерів має бути не меншою, ніж 1,65 м3 /с.
29-04-2015, 00:34
