Средняя высота водосбора
Для установления средней высоты бассейна существует как минимум два способа: можно определить ее по гипсографической кривой бассейна или вычислить по формуле (8):
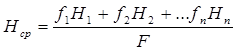 ,
,
где Нср – средняя высота водосбора, м; f1 , f2, …fn – частные площади водосбора, заключенные между горизонталями, км2 ; Н1 , Н2 , …Нn – средние высоты между горизонталями, м; F – общая площадь водосбора, км2 . Для определения Нср в случае водосбора р. Кегеты удобнее воспользоваться первым способом, поскольку вычисление частных площадей f между всеми горизонталями, как того требует второй способ, представляется затруднительным.
Гипсографическая кривая дает наглядное представление о распределении площади бассейна по высотным зонам. Для ее построения весь диапазон высот в бассейне разбивается на 8 высотных ступеней и измеряются площади, расположенные между горизонталями с отметками этих ступеней и линией водораздела. Чем больше амплитуда высоты в бассейне, тем большие интервалы высоты берутся для отдельных ступеней.
Наивысшей точкой бассейна Кегеты является точка с отметкой 4444 м, минимального значения высота достигает в районе створа – 1500 м, амплитуда составляет 2944 м. В соответствие с методикой, этот интервал следует разбить на 8 высотных ступеней. Полученные таким образом значения горизонталей послужили основой разбиения площади бассейна, представленного на рис. 7. Высотные отметки горизонталей и результаты вычисления площадей, заключенных между ними, приведены в табл. 3.
По данным измерений площадей и отметкам горизонталей строится график распределения площадей по высотным зонам, показывающий размеры площадей, лежащих между высотными отметками. Он имеет вид столбчатой диаграммы, по горизонтали откладываются площади, по вертикали – высотные отметки. Для Кегеты этот график представлен на рис. 8.
После того как график распределения площадей построен, строится кривая нарастания площадей по высотным зонам – гипсографическая кривая, которая может быть получена путем последовательного суммирования площадей, отложенных по оси абсцисс на предыдущем графике. Точки гипсографической кривой откладываются на нижних границах высотных интервалов и соединяются плавной линией. На графике под масштабом площадей наносится шкала процентов из расчета, что общая площадь бассейна равна 100%. Точке на кривой с абсциссой 50% и будет соответствовать высота на оси ординат, которую можно считать средней высотой водосбора. Гипсографическая кривая бассейна р. Кегеты построена на рис. 9
Таблица 3. Ведомость измерения площадей высотных зон бассейна р. Кегеты
| № | Высотные отметки горизонталей, м | Площадь высотной зоны, км2 | |
| От | До | ||
1 2 3 4 5 6 7 8 |
4000 3600 3200 2800 2400 2000 1600 1500 |
4444 4000 3600 3200 2800 2400 2000 1600 |
10,4 17 26 18,6 25 24 34 23 |
Геоморфологические коэффициенты
К геоморфологическим коэффициентам относятся коэффициент озерности, коэффициент заболоченности и коэффициент залесенности. Они рассчитываются соответственно как процентное отношение суммарной площади озер, болот и лесов, расположенных в бассейне некоторой реки, к площади водосбора этой реки. Например, коэффициент озерности определяется по формуле (9):
![]() ,
,
Насколько можно установит по карте на рис. 1, бассейн р. Кегеты содержит озеро. Леса не отображены на карте.
2.2 Климатические факторы стока
Осадки
Распределение осадков по поверхности суши зависит от удаления местности от океана, рельефа местности и растительного покрова. По мере удаления от океана количество постепенно уменьшается. В горных районах склоны, обращенные к влагоносным ветрам, получают больше осадков, чем противоположные. Влияние рельефа сказывается в том, что с повышением местности количество выпадающих осадков обычно увеличивается. Увеличение количества осадков с высотой обычно происходит до отметок 3000 – 3500 м над уровнем моря, а выше эта зависимость уменьшается или прекращается.
Опираясь на карты источника, можно отметить большую увлажненность бассейна Кегеты осадками ввиду благоприятных условий географического расположения. Среднегодовые суммы осадков здесь на большей части территории на высотах от 1300–1400 м до 2300–2500 м превышают 1000 мм. Выше и ниже этих пределов осадков выпадает меньше, и при подъеме по юго-западному склону Кыргызского хр. до высот 3500 – 3800 м их количество уменьшается до 600 мм.
Испарение
Процесс испарения состоит в том, что вода из жидкого или твердого состояния переходит в газообразное. К факторам, увеличивающим испарение, относятся повышение температуры и увеличение скорости ветра, усиливающее турбулентное перемешиванию масс воздуха, соприкасающихся с испаряющей поверхностью. Кроме того, на интенсивность испарения влияет влажность почвы, солнечная радиация, которые обуславливают жизнь растений и их рост, парциальное давление (упругость) водяного пара в воздухе и др.
Температура в долине р. Кегеты в среднем уменьшаются с высотой от +20 до +10 °С в июле и от -4 до -14 °С в январе. Средняя влажность в июле составляет 40 – 55%, а в январе – 55 – 60%. Среднегодовая испаряемость в бассейне Кегеты равномерно уменьшается от низовий к верховьям от 1200–1300 мм до 600 мм. В целом, бассейн Кегеты по классификации В. Кеппена и А.В. Вознесенского относится к бореальному типу климата с ясно выраженной зимой и летом и достаточным увлажнением, и лишь высокогорные участки Кыргызского хребта имеют холодный тундровый тип климата.
3. Сток и его распределение
3.1 Определение нормы годового стока и его статистических характеристик
Нормой годового стока Q0 называется среднее его значение за многолетний период такой продолжительности, при увеличении которой полученное среднее существенно не меняется, включающий несколько полных четных циклов колебаний водности реки при неизменных географических условиях и одинаковом уровне хозяйственной деятельности в бассейне реки. Норма годового стока, или средний многолетний сток, является основной и устойчивой характеристикой, определяющей общую водность рек и потенциальные водные ресурсы данного бассейна или района.
Согласно «Указаниям по определению расчетных гидрологических характеристик» (СН 435–72) /7,8,13/, продолжительность периода наблюдений считается достаточной для установления расчетных значений нормы годового стока, если рассматриваемый период репрезентативен и относительная средняя квадратическая ошибка многолетней величины eQ 0 не превышает 5…10%, а коэффициент вариации (изменчивости) eсv – 10…15%.
Норма годового стока, как всякая средняя арифметическая величина статистического ряда, может быть определена по формуле:
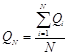
![]() , (17)
, (17)
где QN - норма годового стока, Qi – годовые значения стока за длительный период (N лет).
Среднегодовой расход воды р. Кегаты за 1927–1975
| год | Qi , м3 /с | Год | Qi , м3 /с | год | Qi , м3 /с |
1927 1928 1929 1930 1931 1932 1933 1934 1935 1936 1937 1938 1939 1940 1941 1942 1943 1944 1945 1946 |
- - - - - 2.51 2.55 2.60 2.35 2.12 2.15 1.58 2.11 2.37 2.43 3.46 1.81 1.80 2.22 2.45 |
1947 1948 1949 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959 1960 1961 1962 1963 1964 1965 1966 |
1.88 2.15 3.02 2.46 2.00 2.43 2.28 2.29 2.97 2.98 2.16 2.35 2.47 2.08 2.30 2.99 2.23 2.56 2.16 3.01 |
1967 1968 1969 1970 1971 1972 1973 1974 1975 |
2.67 2.30 2.88 3.56 2.30 2.72 2.64 1.96 2.26 |
Вследствие недостаточной длины рядов наблюдений за годовым стоком (как правило не превышают 60…80 лет, составляя в основном 20…40 лет) норма годового стока, определенная по (17) отличается от истинного среднего значения QN на величину σQn тогда:
QN =Q0 n ±σQn , (18)
где Q0 n – средний годовой сток за ограниченный период наблюдений; σQn – средняя квадратическая ошибка n-летней средней.
Cогласно теории ошибок, величина σQn , на которую отличается среднее значение годового стока за n лет от истинной нормы QN за N лет при N®∞, равна
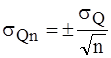 (19)
(19)
где σQ – среднее квадратическое отклонение единичных значений годового стока Qi от среднего за n лет.
Определяется σQ по формуле
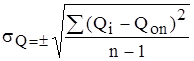 . (20)
. (20)
Для сравнения точности определения нормы стока рек различной водности пользуются относительным значением средней квадратической ошибки. Так, выражая σQ в процентах от Q0n получим среднюю, квадратическую ошибку нормы стока, вычисленную по ограниченному ряду n лет,
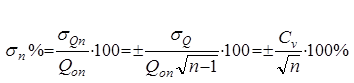 , (21)
, (21)
где ![]() – коэффициент вариации ряда годовых значений стока за n лет.
– коэффициент вариации ряда годовых значений стока за n лет.
Коэффициент вариации CV характеризует колебания годовых значений стока относительно их средней величины. Он является безразмерной характеристикой изменчивости годового стока, удобной для сравнения нескольких рядов наблюдений, различающихся своими средними значениями. При выражении отдельных членов ряда в безразмерных модульных коэффициентах Ki коэффициент вариации определяется по формуле
![]()
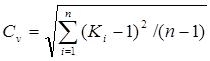 . (22)
. (22)
Поскольку в колебаниях годового стока наблюдается определенная цикличность, проявляющаяся в последовательной смене групп многоводных и маловодных лет, то среднеарифметическое из многолетнего ряда наблюдений считается нормой только в случае, если ряд состоит из полных циклов колебаний водности.
Цикл – это сочетание многоводных, маловодных и средних по водности лет. Включение в расчетный период наблюдений одной многоводной фазы дает преувеличение, только маловодной фазы – преуменьшение нормы стока.
Расчетный (репрезентативный) период устанавливается во всех случаях, когда продолжительность наблюдений не превышает 50–60 лет. Он включает наибольшее число законченных циклов, состоящих из групп многоводных и маловодных лет. Принимаются во внимание лишь основные продолжительные циклы, распространяющиеся на большие территории и охватывающие все реки данного района.
Цикличность колебаний стока и расчетный период для определения нормы стока устанавливают с помощью разностных суммарных кривых годового стока. Наиболее удобно строить суммарные кривые в относительных величинах – модульных коэффициентах К.
Расчеты по определению нормы стока, коэффициента вариации CV и для построения суммарной кривой удобнее свести в таблицу 7.
По выше приведенным формулам и по данным таблицы 7 определяют Q0 и Cv . По значениям графы 6 строится зависимость S(k-1)=f(t). Пример такой кривой приведен на рисунке 9.
Таблица 7
| № | год | ср. г.расх. | мод. коэф.K | K i -1 | ∑(K i -1) | (K i -1)² |
| 1 | 1932 | 2,51 | 1,05 | 0,0493 | 0,0493 | 0,00 |
| 2 | 1933 | 2,55 | 1,07 | 0,07 | 0,12 | 0,00 |
| 3 | 1934 | 2,60 | 1,09 | 0,09 | 0,20 | 0,01 |
| 4 | 1935 | 2,35 | 0,98 | -0,02 | 0,18 | 0,00 |
| 5 | 1936 | 2,12 | 0,89 | -0,11 | 0,08 | 0,01 |
| 6 | 1937 | 2,15 | 0,90 | -0,10 | -0,02 | 0,01 |
| 7 | 1938 | 1,58 | 0,66 | -0,34 | -0,36 | 0,12 |
| 8 | 1939 | 2,11 | 0,88 | -0,12 | -0,48 | 0,01 |
| 9 | 1940 | 2,37 | 0,99 | -0,01 | -0,48 | 0,00 |
| 10 | 1941 | 2,43 | 1,02 | 0,02 | -0,47 | 0,00 |
| 11 | 1942 | 3,26 | 1,36 | 0,36 | -0,11 | 0,13 |
| 12 | 1943 | 1,81 | 0,76 | -0,24 | -0,35 | 0,06 |
| 13 | 1944 | 1,80 | 0,75 | -0,25 | -0,60 | 0,06 |
| 14 | 1945 | 2,22 | 0,93 | -0,07 | -0,67 | 0,01 |
| 15 | 1946 | 2,45 | 1,02 | 0,02 | -0,64 | 0,00 |
| 16 | 1947 | 1,88 | 0,79 | -0,21 | -0,86 | 0,05 |
| 17 | 1948 | 2,15 | 0,90 | -0,10 | -0,96 | 0,01 |
| 18 | 1949 | 3,02 | 1,26 | 0,26 | -0,70 | 0,07 |
| 19 | 1950 | 2,46 | 1,03 | 0,03 | -0,67 | 0,00 |
| 20 | 1951 | 2,00 | 0,84 | -0,16 | -0,83 | 0,03 |
| 21 | 1952 | 2,43 | 1,02 | 0,02 | -0,82 | 0,00 |
| 22 | 1953 | 2,28 | 0,95 | -0,05 | -0,86 | 0,00 |
| 23 | 1954 | 2,29 | 0,96 | -0,04 | -0,91 | 0,00 |
| 24 | 1955 | 2,97 | 1,24 | 0,24 | -0,66 | 0,06 |
| 25 | 1956 | 2,98 | 1,25 | 0,25 | -0,42 | 0,06 |
| 26 | 1957 | 2,16 | 0,90 | -0,10 | -0,52 | 0,01 |
| 27 | 1958 | 2,35 | 0,98 | -0,02 | -0,53 | 0,00 |
| 28 | 1959 | 2,47 | 1,03 | 0,03 | -0,50 | 0,00 |
| 29 | 1960 | 2,08 | 0,87 | -0,13 | -0,63 | 0,02 |
| 30 | 1961 | 2,30 | 0,96 | -0,04 | -0,67 | 0,00 |
| 31 | 1962 | 2,99 | 1,25 | 0,25 | -0,42 | 0,06 |
| 32 | 1963 | 2,23 | 0,93 | -0,07 | -0,49 | 0,00 |
| 33 | 1964 | 2,56 | 1,07 | 0,07 | -0,42 | 0,00 |
| 34 | 1965 | 2,16 | 0,90 | -0,10 | -0,51 | 0,01 |
| 35 | 1966 | 3,01 | 1,26 | 0,26 | -0,26 | 0,07 |
| 36 | 1967 | 2,67 | 1,12 | 0,12 | -0,14 | 0,01 |
| 37 | 1968 | 2,30 | 0,96 | -0,04 | -0,18 | 0,00 |
| 38 | 1969 | 2,88 | 1,20 | 0,20 | 0,03 | 0,04 |
| 39 | 1970 | 2,56 | 1,07 | 0,07 | 0,10 | 0,00 |
| 40 | 1971 | 2,30 | 0,96 | -0,04 | 0,06 | 0,00 |
| 41 | 1972 | 2,72 | 1,14 | 0,14 | 0,19 | 0,02 |
| 42 | 1973 | 2,64 | 1,10 | 0,10 | 0,30 | 0,01 |
| 43 | 1974 | 1,96 | 0,82 | -0,18 | 0,12 | 0,03 |
| 44 | 1975 | 2,26 | 0,94 | -0,06 | 0,06 | 0,00 |
| ∑ Qi = | 102,86 | ∑Ki = | ∑(Ki -1) = | ∑(Ki -1)²= | ||
| Qn = ∑Qi / n = | 2,39 | 43,00 | 0,00 | 1,00 |
| Q on = | 2,391 | |
| σ = | 0,309 | |
| Cv = | 0,129 | |
| ε Q% = | 1,656 | < 5…10% |
| ε Cv % = | 9,129 | <10…15% |
| 9,028 | <10…15% | |
| Q N = Q on | ||
При водохозяйственном планировании, строительном и энергетическом проектировании, которые предусматривают естественный или видоизмененный режим речного стока, необходимо знать не только среднюю величину (норму) стока, но и сток маловодных и многоводных лет, а также пределы возможных колебаний годового стока в будущем многолетнем периоде.
Если бы колебания стока имели определенную периодичность и был бы известен закон колебаний, то по имеющимся данным наблюдений можно было бы установить хронологический ход стока на заданный будущий период времени и определить, когда будет наблюдаться та или иная величина стока или сколько раз за это время годовой сток превысит то или иное значение. Но такая задача пока неразрешима. Поэтому расчеты годового стока и других его характеристик представляются в виде количественной оценки отвечающей той или иной заданной обеспеченности или повторяемости – в среднем один раз в N лет без указания срока наступления расчетной величины.
Обеспеченностью гидрологической величины называется вероятность того, что рассматриваемое ее значение может быть превышено. При этом различают:
- вероятность превышения для явлений, наблюдаемых только один раз в году;
– вероятность превышения среди совокупности всех возможных значений для явлений, которые могут наблюдаться несколько раз в году;
– вероятность превышения в рассматриваемом пункте или на рассматриваемой территории в любом пункте.
Вероятность служит мерой оценки достоверности появления того или иного значения рассматриваемой характеристики или явления.
Различают теоретическую вероятность (lim m/n=p) и эмпирическую вероятность или частность (m/n), выявляемую из наблюдений частоты появления благоприятных случаев, составляющих очень длинный ряд.
Для установления эмпирической обеспеченности членов ограниченного ряда, которая бы в большой мере отвечала теоретической обеспеченности, предложено несколько формул, среди них формулы:
С.Н. Крицкого и М.Ф. Менкеля /4/
p=(m/(n+1)) 100% (23)
Н.Н. Чегодаева
p=((m-0.3)/(n+0.4)) 100% (24)
Формула (23) выведена в предположении, что используемый в расчетах ряд, охватывающий ni – летний период, среди других n – летних периодов, составляющих генеральную совокупность, характеризуется повышенной водностью высоких расходов и пониженной низких. Она дает некоторый запас (завышение) в верхней части кривой обеспеченности и рекомендуется для расчетов максимальных расходов.
Формула (24) основана на предположении, что рассматриваемый ni – летний период по своей водности занимает медианное положение среди других n – летних периодов. Эта формула дает запас (занижение) в нижней части кривой обеспеченности и рекомендуется при расчетах годового, сезонного и минимального стока.
Для построения теоретических кривых обеспеченности, которые соответствовали бы эмпирическим кривым, необходимо по данным наблюдений вычислить значения параметров их дифференциального уравнения и произвести его интегрирование.
Практически достаточно установить три основных параметра теоретической кривой распределения – среднюю многолетнюю величину (норму) Q, которая, будучи выражена в относительных единицах – модульных коэффициентах K, равна единице; коэффициент изменчивости (вариации) Cv ; коэффициент асимметрии Cs , по которым могут быть построены теоретические кривые обеспеченности годового стока по формуле /2,4/:
Kр% =Фр% ×Cv +1 (25)
где Фр% = – Фр% (Cs , p% ), функция Фостера принимается по табл.
Теоретическую кривую обеспеченности необходимо сопоставить с данными непосредственных наблюдений, вычисленными по формулам 23 или 24. Если точки эмпирической обеспеченности, нанесенные на график теоретической кривой обеспеченности, осредняют последнюю, значит она соответствует действительности. Несоответствие эмпирических точек и теоретической кривой обеспеченности указывает на неправильность определения параметров кривой, в первую очередь на неточность определения коэффициента асимметрии Cs. В этом случае необходимо изменить соотношение Cs и Cv и вновь построитьтеоретическую кривую обеспеченности.
Кривая обеспеченности стока, построенная в простых координатах, имеет большую кривизну в верхних и нижних частях. Это затрудняет пользование кривой и графическую экстраполяцию крайних участков кривой, представляющий наибольший интерес при гидрологических расчетах. Поэтому для построения кривой обеспеченности применяют специальную клетчатку вероятностей. Основное свойство клетчатки вероятностей состоит в том, что на ней кривая обеспеченности с коэффициентом асимметрии Cs =0 получает вид прямой. При других значениях Cs кривые обеспеченности, построенные на клетчатке вероятностей, имеют вид плавных линий, причем кривизна их увеличивается с увеличением коэффициента асимметрии.
На рисунке 10 приведена аналитическая и эмпирическая кривые обеспеченности годового стока на клетчатке вероятности с обычной вертикальной шкалой.
Для построения эмпирической кривой обеспеченности расчеты удобнее выполнять, в форме табл. 8.
Таблица 8
| № | год | ср. г.расх. | Qi в порядке | P% |
| убывания | ||||
| 1 | 1932 | 2,51 | 3,26 | 1,58 |
| 2 | 1933 | 2,55 | 3,02 | 3,83 |
| 3 | 1934 | 2,60 | 3,01 | 6,08 |
| 4 | 1935 | 2,35 | 2,99 | 8,33 |
| 5 | 1936 | 2,12 | 2,98 | 10,59 |
| 6 | 1937 | 2,15 | 2,97 | 12,84 |
| 7 | 1938 | 1,58 | 2,88 | 15,09 |
| 8 | 1939 | 2,11 | 2,72 | 17,34 |
| 9 | 1940 | 2,37 | 2,67 | 19,59 |
| 10 | 1941 | 2,43 | 2,64 | 21,85 |
| 11 | 1942 | 3,26 | 2,60 | 24,10 |
| 12 | 1943 | 1,81 | 2,56 | 26,35 |
| 13 | 1944 | 1,80 | 2,56 | 28,60 |
| 14 | 1945 | 2,22 | 2,55 | 30,86 |
| 15 | 1946 | 2,45 | 2,51 | 33,11 |
| 16 | 1947 | 1,88 | 2,47 | 35,36 |
| 17 | 1948 | 2,15 | 2,46 | 37,61 |
| 18 | 1949 | 3,02 | 2,45 | 39,86 |
| 19 | 1950 | 2,46 | 2,43 | 42,12 |
| 20 | 1951 | 2,00 | 2,43 | 44,37 |
| 21 | 1952 | 2,43 | 2,37 | 46,62 |
| 22 | 1953 | 2,28 | 2,35 | 48,87 |
| 23 | 1954 | 2,29 | 2,35 | 51,13 |
| 24 | 1955 | 2,97 | 2,30 | 53,38 |
| 25 | 1956 | 2,98 | 2,30 | 55,63 |
| 26 | 1957 | 2,16 | 2,30 | 57,88 |
| 27 | 1958 | 2,35 | 2,29 | 60,14 |
| 28 | 1959 | 2,47 | 2,28 | 62,39 |
| 29 | 1960 | 2,08 | 2,26 | 64,64 |
| 30 | 1961 | 2,30 | 2,23 | 66,89 |
| 31 | 1962 | 2,99 | 2,22 | 69,14 |
| 32 | 1963 | 2,23 | 2,16 | 71,40 |
| 33 | 1964 | 2,56 | 2,16 | 73,65 |
| 34 | 1965 | 2,16 | 2,15 | 75,90 |
| 35 | 1966 | 3,01 | 2,15 | 78,15 |
| 36 | 1967 | 2,67 | 2,12 | 80,41 |
| 37 | 1968 | 2,30 | 2,11 | 82,66 |
| 38 | 1969 | 2,88 | 2,08 | 84,91 |
| 39 | 1970 | 2,56 | 2,00 | 87,16 |
| 40 | 1971 | 2,30 | 1,96 | 89,41 |
| 41 | 1972 | 2,72 | 1,88 | 91,67 |
| 42 | 1973 | 2,64 | 1,81 | 93,92 |
| 43 | 1974 | 1,96 | 1,80 | 96,17 |
| 44 | 1975 | 2,26 | 1,58 | 98,42 |
Для построения теоретической кривой обеспеченности необходимо определить величины расходов, имеющих обеспеченность Р = 0,01%, 0,1%, 1%, 5%, … 99,9% по формуле 25. Полученные значения удобнее свести в табл. 9
Таблица 9
| Р% | 0,1 | 1 | 5 | 99,9 |
| ФP % | ||||
| KP % | ||||
| QP % |
В работе необходимо вычислить значения расхода с вероятностью Р = 0,05%, 0,2%, 1%, 50%, 75% и 90%.
3.2 Характеристики годового стока
Сток – это движение воды по поверхности, а также в толще почв и горных пород в процессе ее круговорота в природе. При расчетах под стоком понимается количество воды, стекающей с водосбора за какой-либо период времени. Это количество воды может быть выражено в виде расхода `Q, объема W, модуля M или слоя стока h.
Объем стока W– количество воды, стекающей с водосбора за какой-либо период времени (сутки, месяц, год и т.п.), – определяется по формуле
W=`Q×T [м3 ], (19)
где `Q – средний расход воды за расчетный период времени, м3 /с, T – число секунд в расчетном периоде времени.
Так как средний расход воды был вычислен ранее как норма годового стока, объем стока р. Кегеты за год W = 2.39∙365,25∙24∙3600 = 31764096м3 .
Модуль стока М – количество воды, стекающей с единицы площади водосбора в единицу времени, – определяется по формуле
М=103 `Q/F [л/(с×км2 )], (20)
где F– площадь водосбора, км2 .
Модуль стока р. Кегеты М=103 ∙ 2.39/178 = 13.42 л/(с×км2 ).
Слой стока h мм – количество воды, стекающей с водосбора за какой-либо период времени, равное толщине слоя, равномерно распределенного по площади этого водосбора, – определяется по формуле
h=W/(F 103 )=`Q×T/(F 103 ). (21)
Слой стока для бассейна р. Кегеты h = 31764096/ (178 ∙103 ) = 178.44 мм.
К безразмерным характеристикам относятся модульный коэффициент и коэффициент стока.
Модульный коэффициент К представляет собой отношение стока за какой либо конкретный год к норме стока:
К = Qi /Q0 = Wi /W0 = hi /h0 , (22)
и для р. Кегеты за рассматриваемый период К меняется от К =1.58 / 2.39= 0.66 для года с минимальным расходом до К = 3.26 / 2.39 = 1.36 для максимального расхода.
Коэффициент стока a – отношение объема или слоя стока к количеству выпавших на площадь водосбора осадков х, обусловивших возникновение стока:
a = h/x. (23)
Коэффициент стока показывает, какая часть осадков идет на образование стока.
В курсовой работе необходимо определить характеристики годового стока для принятого к рассмотрению бассейна, приняв норму стока из раздела
3.3 Внутригодовое распределение стока
Внутригодовое распределение стока рек занимает важное место в вопросе изучения и расчетов стока как в практическом, так и в научном отношении, являясь в тоже время наиболее сложной задачей гидрологических исследований /2,4,13/.
Основные факторы, определяющие внутригодовое распределение стока и его общую величину, – климатические. Они определяют общий характер (фон) распределения стока в году того или иного географического района; территориальные изменения распределения стока следуют за изменением климата.
К факторам, влияющим на распределение стока в течении года относятся озерность, лесистость, заболоченность, размеры водосборов, характер почв и грунтов, глубина залегания грунтовых вод, и т.д., которые в определенной мере должны учитываться в расчетах как при отсутствии, так и при наличии материалов наблюдений.
В зависимости от наличия данных гидрометрических наблюдений применяются следующие методы расчета внутригодового распределения стока:
1) при наличии наблюдений за период не менее 10 лет: а) распределение по аналогии с распределением реального года; б) метод компоновки сезонов;
2) при отсутствии или недостаточности (менее 10 лет) данных наблюдений: а) по аналогии с распределением стока изученной реки-аналога; б) по районным схемам и региональным зависимостям параметров внутригодового распределения стока от физико-географических факторов.
Внутригодовое распределение стока обычно рассчитывается не по календарным годам, а по водохозяйственным, начиная с многоводного сезона. Границы сезонов назначаются едиными для всех лет с округлением до месяца.
Расчетная вероятность превышения стока за год, лимитирующие период и сезон назначается в соответствии с задачами водохозяйственного использования стока реки.
В курсовой работе необходимо выполнить расчеты при наличии гидрометрических наблюдений.
Расчеты внутригодового распределения стока методом компоновки
Исходными данными для расчета являются среднемесячные расходы воды и в зависимости от цели использования расчета – заданный
29-04-2015, 00:48
