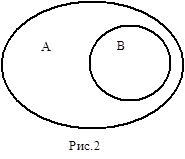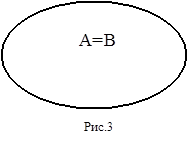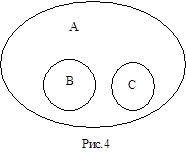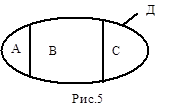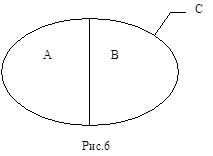Лекции по Логике

ВВЕДЕНИЕ

Один из героев Мольера только под конец жизни узнал, что говорит прозой. Но отсутствие знания об этом ему не мешало достаточно красноречиво выражать свои мысли. Даже если человек не знает правил грамматики родного ему языка, окружающие его люди в большинстве ситуаций смогут понять то, о чём он говорит. Но это вовсе не значит, что изучать грамматику не нужно. Так и с логикой. Интуитивно большинство из нас в обыденной жизни рассуждает вполне логично и без знания логики. Но иногда и в обыденной жизни встречаются такие ситуации, в которых стихийно сложившихся навыков логичного мышления уже не хватает. Предположим, кто - то в разговоре с вами проводит следующее рассуждение: “Я - человек. Ты - не я. Следовательно, ты - не человек”. Что большинство из нас сможет ответить на такой вывод? В лучшем случае ответом будет фраза: “Сам дурак”. Но в этом случае вы рискуете “потерять лицо”, ибо одно дело балансировать на грани оскорбления, не переступая эту грань, а другое дело - прямо оскорблять. Ответ по форме должен соответствовать выпаду. Достойным ответом в этой ситуации было бы высмеять противника, показав, что с его знаниями логики лучшее, что ему остаётся делать - это пасти гусей в колхозе, а не появляться в приличном обществе. Но для того, чтобы показать несостоятельность приведённого рассуждения, нужно суметь проанализировать его, а именно этому и учит логика.

В профессиональной же деятельности, особенно деятельности юриста, ситуаций, когда интуитивных навыков логичного мышления будет не хватать, более, чем достаточно. И в большинстве этих ситуаций нужно будет действовать, не задумываясь. Для этого необходимо не только знать законы логики, а, ещё раз следует подчеркнуть это, уметь применять их не задумываясь, автоматически, так же, как вы используете математические навыки в магазине. А такие навыки появляются только путём “тренировок”, т.е. решения задач. Поэтому важно не только помнить изученный материал, но и активно применять эти знания в житейских и профессиональных ситуациях.

ТЕМА 1

ПРЕДМЕТ И ЗАДАЧИ ЛОГИКИ

Предмет логики

Предмет всякой науки становится вполне ясным только после изучения самой науки. Однако некоторое предварительное указание на то, что изучает логика, необходимо.

Логика изучает мышление, но не всякое мышление, а лишь те мыслительные процессы, которые направлены на обнаружение и обоснование истины, на решение некоторых задач. Истина же достигается посредством рассуждений, причём не любых, а только правильных рассуждений. Поэтому логика занимается изучением правильных рассуждений. Что же такое правильное рассуждение? Это рассуждение, которое при истинных посылках, т.е. исходных данных, необходимо приводит к истинному выводу.

Логика изучает формы правильных рассуждений, но не их содержание. Содержание мысли бесконечно разнообразно, но всё это разнообразие укладывается в небольшое число форм. Именно эти формы и изучает логика. В этом отношении логика сходна с грамматикой. Последняя тоже изучает формы языковых выражений, отвлекаясь от их содержания. Возникает вопрос: а почему логика занимается именно формой рассуждений, а не содержанием? Ответ состоит в том, что правильность рассуждения зависит только от формы этого рассуждения . На этом принципе построена вся логика. Форма, а не содержание обеспечивает доступ к истине.

Таким образом, можно сделать вывод, что логика изучает законы и формы познающего мышления, т.е. такого мышления, которое направлено на отыскание истины.

Значение логики

Помимо того, что логика красивая наука, которую приятно изучать саму по себе, существует ещё несколько практических причин, по которым полезно изучать логику.

Занятия логикой приучают точно мыслить и ясно их излагать.

Логика учит анализировать свои и чужие рассуждения.

Логика воспитывает умение убеждать и обосновывать свои идеи.

Наконец, логика учит спорить.

Тема 2

Понятие как форма мышления

Признаки

В мире огромное количество предметов: люди, слоны, розы, кирпичи, корабли и т.д. Перечислять можно до бесконечности. Каждый предмет чем - то похож и чем - то отличается от других предметов. Например, что общего у слона и дирижабля? Вот один из возможных ответов: каждый из них имеет какой-то цвет. Спрашивать же, чем отличается слон от дирижабля, нет нужды, они друг от друга отличаются слишком многим: размером, весом, формой и т.п. То, чем предметы сходны между собой или чем они отличаются друг от друга, называется признаками предмета . Размер, цвет, форма, вес - всё это признаки. Каждый предмет имеет огромное число признаков. Слон может быть чёрным, серым, грязным, без бивней, с порванным левым ухом, весом в 1,5 т, живущим в зоопарке Лондона, поднявшим в данный момент правую переднюю ногу на высоту 1 фут 3 дюйма над землёй. Всё, что перечислено в последнем предложении после слов “может быть” - признаки, в данном случае слона. Если бы мы захотели назвать все признаки, которые может иметь слон, нам не хватило бы жизни. Может возникнуть вопрос: для чего так подробно останавливаться на столь очевидных вещах? Дело в том, что с признаком связана такая важная в логике “вещь”, как понятие .

Определение понятия

Слово “понятие” имеет общий корень со словом “понимание”, и, наверное, эти слова обозначают нечто близкое между собой. В самом деле, мы понимаем что-то, когда имеем об этом понятие, и наоборот, имеем понятие, когда выполнили акт понимания. Так что же такое понятие? Логика нам предлагает следующий ответ на этот вопрос. Понятие - форма мысли, отображающая предметы и явления в их наиболее общих и существенных признаках . Поясним термины, входящие в это определение.

Форма мысли . В данном случае синонимами выражения “форма мысли” могут быть “разновидность мысли”, “способ мышления”. Дать определение мысли очень трудно, хотя все интуитивно понимают, что это такое. Это нечто, что вертится у нас в голове, что нельзя потрогать, увидеть, измерить и что делает нас людьми. Неважно, что мы не можем дать точного определения мысли. Важно то, что мысль может быть разных видов. В логике изучают три формы (виды) мысли: понятие, суждение, умозаключение.

Форма мысли, отображающая предметы и явления . Французский философ Рене Декарт считал, что существует два вида явлений: мыслительные и материальные. Основной признак материи состоит в её протяжённости в пространстве, тогда как мысль пространства не занимает. В каком виде существует мысль в нас, никто не знает, но тем не менее существует связь между материальным миром и сознанием. Эту связь между мыслью о предмете и самим предметом принято называть отображением, т.е. говорят, что предмет отображается в сознании. То, о чём человек думает, мыслит, называется предметом мысли .

Форма мысли, отображающая предметы и явления в их наиболее общих и существенных признаках. Эта фраза говорит о том, что предметом мысли, т.е. то, о чём думается, на чём сосредоточено внимание, являются общие и существенные признаки предметов и явлений. Что такое признак, уже известно. Что такое общий признак , тоже нетрудно понять. Это признак, принадлежащий нескольким предметам. На основании общего признака предметы, обладающие им, можно объединить в группу, класс, множество. Таким образом, класс , множество - это объединение предметов на основании присущего предметам общего признака. Например, снег, лист бумаги, сахар образуют класс предметов с общим признаком “быть белым”.

Существенный признак - это признак, необходимо присущий предмету, лишившись которого, предмет перестанет существовать. Несущественный признак может приобретаться или теряться, но это никак не скажется на существовании данного предмета. Например, вода может быть холодной, прозрачной, пресной. Если мы лишим воду этих свойств, то она станет тёплой, мутной, солоноватой. Не изменится одно. Вода не перестанет быть водой. Но если мы отнимем у воды признак “быть жидкостью”, то вода превратится в лёд или пар, поскольку “быть жидкостью” - существенный признак воды.

Таким образом, когда мы произносим фразу “форма мысли, отображающая предметы и явления в их наиболее общих и существенных признаках”, то предполагаем сосредоточение, с одной стороны, на том, что объединяет предмет мысли с другими предметами, а с другой стороны, – на том главном, что отличает его от всех других предметов.

Понятие нельзя путать с представлением. Представление - это образ предмета, “картинка”, возникающая у человека в голове, и эта “картинка” всегда конкретна. Если нескольких людей попросить представить себе дом, то у одного всплывёт в сознании деревенская изба, у другого - пятиэтажка, у третьего - коттедж с подземным гаражом и бассейном. В понятии же дома ничего этого нет, в нём присутствует лишь общее и существенное для всех домов: это жилище человека, защищающее его от непогоды и от непрошенных гостей. А общее представить себе нельзя, можно представить только конкретное. Поэтому нельзя представить понятие. Понятие можно только помыслить. И отсюда можно сделать интересный вывод - мышление всегда ненаглядно.

В языке понятия выражаются отдельными словами и словосочетаниями: “стол”, “гора”, “остров сокровищ”, “река в Африке”. Слово, обозначающее понятие, называется именем . Полезно иметь в виду, что каждое понятие обязательно выражается в каком-то слове, но одно и то же слово естественного языка может выражать разные понятия, например, слово “ключ”: это и ключ от квартиры, где деньги лежат, и ключ в лесу, из которого можно напиться в жаркую погоду.

Каждое понятие характеризуется содержанием и объёмом . Содержание понятия - это совокупность существенных признаков предмета мысли. Объём понятия - это множество предметов, признаки которых составляют содержание понятия. Например, в объём понятия “дерево” войдут все существующие на земле деревья: дубы, берёзы, ивы и т.д. Содержанием же этого понятия будут общие и существенные признаки деревьев: быть растением, иметь ствол, крону, корневую систему. По объёму все понятия делятся на три вида: общие, единичные, пустые (нулевые).

Общее понятие - это понятие, в объём которого входит несколько (два и более) предметов. Примеры: стол, дом, житель Земли, подгоревшая манная каша.

Единичное понятие - понятие, в объём которого входит только один предмет. Примеры: первый космонавт, столица Франции, Луна.

Пустое понятие - понятие, в объём которого не входит ни один реально существующий предмет. При определении понятия как пустого необходимо чётко представлять, что в данном случае подразумевается под реальностью. В обыденной реальности “русалка” - пустое понятие, но если под реальностью подразумевать мир сказок Пушкина, то в этом случае “русалка” - общее понятие.

Между объёмом и содержанием понятия существует взаимосвязь, которая носит название закона обратного отношения между содержанием и объёмом понятия . Этот закон гласит: чем больше признаков включает в себя содержание понятия, тем меньше его объём, и наоборот, чем больше предметов входит в объём понятия, тем меньше признаков в содержании понятия . Рассмотрим два понятия: “человек” и “европеец”. Содержание понятия “европеец” богаче, т.к. к признакам человека вообще здесь ещё добавляются признаки, характеризующие европейца, однако по объёму понятие “европеец” меньше понятия “человек”.

Тема 3

Виды понятий и отношения между ними

Если в содержании двух понятий имеются общие признаки, то их объёмы можно сравнивать и такие понятия называются сравнимыми . Если же общих признаков, то сравнение объёмов становится бессмысленным и такие понятия называются несравнимыми . Например, можно сравнивать объёмы понятий “синий” и “зелёный”, поскольку оба эти понятия обладают признаком “быть цветом”, но невозможно сравнить объёмы понятий “деньги” и “мужество”.

Сравнимые понятия, в свою очередь, распадаются на две группы: совместимые и несовместимые. Совместимые понятия - это понятия, объёмы которых имеют общие предметы, соответственно, несовместимые понятия не имеют общих предметов. Отношения между объёмами понятий можно изображать с помощью круговых схем, которые называются кругами Эйлера .

На рисунке 1 кружком с буквой А обозначен объём понятия А, кружком с буквой В обозначен объём понятия В. Поскольку видно, что эти кружки пересекаются, то пересекаются и объёмы этих понятий, т.е. объёмы понятий А и В имеют одинаковые элементы.

Виды совместимости

Совместимые понятия могут находиться в отношении:

a) пересечения;

b) подчинения;

c) равнозначности.

Два понятия находятся в отношении пересечения , если объёмы этих понятий имеют общие предметы. Отношение пересечения с помощью кругов Эйлера изображено на рис.1. Примером понятий, находящихся в отношении пересечения, являются понятия “студент” (понятие А) и “спортсмен” (понятие В), поскольку существуют спортсмены, не являющиеся студентами (часть объёма понятия В), есть студенты не спортсмены (часть объёма понятия А), но есть и студенты - спортсмены (общая часть объёмов понятий А и В).

Два понятия находятся в отношении подчинения , если все предметы объёма одного понятия входят в объём другого понятия. Отношение подчинения с помощью кругов Эйлера изображено на рис.2. В отношении подчинения находятся понятия “слон” и “животное”: слоны полностью включаются в класс животных, но не исчерпывают его. Понятие, объём которого содержит объём другого понятия (понятие А), называется родовым (родом) по отношению к понятию с меньшим объёмом. Понятие, объём которого входит в объём другого понятия (понятие В), называется видовым (видом) по отношению к понятию с большим объёмом. Отношение подчинения иногда называют родовидовым отношением. Следует иметь в виду, что понятие, видовое по отношению к некоторому более широкому понятию, может быть родовым по отношению к понятию с меньшим объёмом. Так, понятие “слон” является видовым по отношению к родовому понятию “животное”, но будет родовым по отношению к понятию “африканский слон”.

Два понятия находятся в отношении равнозначности (тождественности ), если объёмы этих понятий состоят из одних и тех же предметов. Отношение тождества с помощью кругов Эйлера изображено на рисунке 3. Примером тождественных понятий являются понятия “квадрат” и “равноугольный ромб”. В естественном языке такие понятия называются синонимами.

Виды несовместимости

Несовместимые понятия могут находиться в отношении:

a) соподчинения;

b) противоположности;

c) противоречия (контрадикторности).

Два понятия (понятия В и С) находятся в отношении соподчинения , если объёмы этих понятий произвольным образом включаются в объём третьего понятия (понятия А). Примером понятий, находящихся в отношении соподчинения, могут служить понятия “берёза” и “сосна”, объёмы которых включаются в объём понятия “дерево”. Несовместимые понятия не имеют общих предметов, поэтому на рис.4 объёмы понятий В и С изображены непересекающимися кругами. Однако они всё-таки сравнимы, т.е. в их содержании имеются общие признаки. Именно эти признаки и составляют содержание родового понятия (А) по отношению к данным понятиям (В и С).

Два понятия (А и С) находятся в отношении противоположности если в содержании этих понятий присутствуют признаки, противоположные по значению. На рис. 5 понятие Д является родовым по отношению к понятиям А, В и С, понятия А и С находятся в отношении противоположности, а понятие В в содержании имеет признак, “средний” по отношению к противоположным признакам понятий А и С. Примером противоположных понятий являются понятия “горячий чайник” (понятие А) - “холодный чайник” (понятие С). Родовым понятием в данном случае (понятием Д) является “чайник”, а противоположными признаками - “горячий” и “холодный”. “Средним” понятием (В) будет понятие “тёплый чайник”.

Два понятия (Аи В) находятся в отношении противоречия (контрадикторности ), если их объёмы полностью исчерпывают объём родового понятия (С) и при этом в содержании одного из понятий присутствует отрицание признака другого понятия. Отрицание признака образуется добавлением частицы “не” к признаку. Таким образом, объём родового понятия делится на две части. Пример контрадикторных понятий: “богатый человек” (А) - “небогатый человек” (В). Родовым понятием (С) является понятие “человек”. Очевидно, что все без исключения люди попадают в одну из этих категорий - “богатый” - “небогатый”.

Тема 4

операции над понятиями

Логической операцией (или просто операцией) называется последовательность логических действий, в результате которых из исходных логических объектов образуются новые объекты. Если речь идёт об операциях над понятиями, то логическими объектами, очевидно, являются понятия. К основным операциям над понятиями относят следующие операции:

1) обобщение понятий;

2) ограничение понятий;

3) деление понятий;

4) определение понятий.

Некоторые логики определение понятий не считают логической операцией, поскольку в результате определения не образуется нового понятия, но тем не менее традиционно определение считают операцией.

Обобщение понятия

Обобщение понятия - логическая операция, состоящая в отбрасывании некоторых признаков из содержания исходного понятия, в результате которой из исходного понятия образуется новое понятие с более бедным содержанием и большим


29-04-2015, 05:18