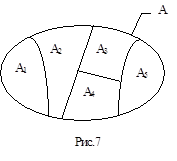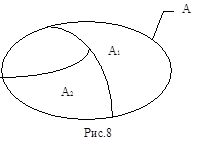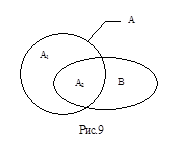Ограничение понятия
Ограничение понятия - логическая операция, состоящая в добавлении некоторых признаков к содержанию исходного понятия, в результате которой из исходного понятия образуется новое понятие с более богатым содержанием и меньшим объёмом по сравнению с исходным понятием. Например, ограничением понятия “автомобиль” будет понятие “легковой автомобиль”, которое получилось из исходного добавлением к содержанию понятия “автомобиль” признаков, характеризующих только легковые автомобили. (Неверно было бы думать, что понятие “легковой автомобиль” получается добавлением к содержанию понятия “автомобиль” признака “легковой”. Слово “легковой” в данном случае обозначает не признак, а совокупность признаков, таких как “вес автомобиля не более 3 т”, “объём двигателя не более 3,5 л”, “максимальное число перевозимых пассажиров не более 7” и т.д. (цифры взяты условно).) Ограничением понятия “легковой автомобиль” может служить понятие “легковой автомобиль марки “мерседес”, ограничением последнего понятия может служить понятие “Голубая акула”, личное имя мерседеса какого-нибудь арабского шейха. Таким образом, пределом ограничения являются единичные понятия, поскольку дальнейшее уменьшение объёма понятия невозможно - остался только один предмет. Дальше можно только расчленять предмет, но это уже не будет ограничением понятия.
Следует ясно представлять себе различие между родо-видовым отношением и отношением части к целому. Для родо-видовых отношений выполняется принцип: всё то, что можно сказать о роде, будет верно и для вида. Для отношения части к целому этот принцип не выполняется: далеко не всё, что можно сказать о целом, будет верно и для его частей. Например, “берёза” есть вид “дерева”, поэтому всё, что можно сказать о дереве вообще, будет верно и для берёзы. Но, скажем, “ствол” - это часть дерева, и то, что можно сказать о дереве, не всегда будет верно для ствола. Например, можно сказать: “Приятно в жаркий полдень отдохнуть в тени дерева”. Но едва ли кто-нибудь скажет: “Приятно в жаркий полдень отдохнуть в тени ствола”.
Деление понятия
К операции деления понятия прибегают тогда, когда возникает задача обзора, систематизации некоторого материала, определения последовательности планируемых действий.
Деление понятия - это логическая операция, в результате которой из исходного понятия образуются несколько новых несовместимых понятий (см. определение несовместимых понятий), совокупность объёмов которых составляет объём исходного понятия.
|
|
Схематично деление понятия изображено на рис. 7. Исходное (делимое) понятие обозначено буквой А, объём которого изображён в виде эллипса. Понятия, образованные в результате деления, обозначены буквами А1 , А2 ,..., А5 . Объёмы этих понятий изображены в виде соответствующих сегментов эллипса.
В операции деления присутствуют три элемента: делимое понятие, основание деления, члены деления.
Делимое понятие - это исходное понятие, объём которого разбивается на части.
Члены деления - это новые понятия, которые образуются в результате деления.
Основание деления - это признак делимого понятия, имеющий конечное число различных состояний, которые являются признаками членов деления. Число состояний основания деления равно числу членов деления, поскольку одно состояние может являться признаком только одного члена деления. Примером деления понятия может служить деление всех людей, имеющих волосы на блондинов, брюнетов, рыжих и шатенов. Делимым понятием в данном случае будет понятие “люди, имеющие волосы”, членами деления будут “блондины”, “брюнеты”, “рыжие” и “шатены”, основанием деления будет признак “цвет волос”.
Правила деления
Чтобы деление не приводило к ошибкам, при совершении деления должны соблюдаться правила деления.
Деление должно быть соразмерным , т.е. сумма объёмов членов деления должна в точности равняться объёму делимого понятия. Нарушение этого правила приводит к ошибкам двух видов.
|
|
Неполное деление - это деление, в результате которого перечисляются не все виды делимого понятия. На рис. 8 делимое понятие обозначено буквой А, выявленные члены деления - буквами А1 и А2 . Сегмент эллипса, никак не обозначенный, представляет объём не выявленных членов деления. Например: “Энергия (А) делится на механическую (А1 ) и химическую (А2 )” (не указаны два вида энергии - электрическая (А3 ) и атомная (А4 )).
|
|
Деление с лишними членами - это деление, в результате которого к объёму делимого понятия добавляются предметы, которые в этот объём первоначально не входили. Схематично эта ситуация изображен на рис. 9. К исходному объёму делимого понятия А, который в результате деления разбит на объёмы членов деления А1 и А2 , добавлен объём понятия В. Например, “химические элементы (А) делятся на металлы (А1 ), неметаллы (А2 ) и сплавы (В)” (сплавы не входят в объём понятия “химический элемент”).
Члены деления должны исключать друг друга , т.е. объёмы членов деления не должны иметь общих элементов. Иначе говоря, каждый элемент объёма делимого понятия должен попасть только в один класс. Пример: “Войны бывают справедливыми, несправедливыми, освободительными, захватническими”. Здесь члены деления не исключают друг друга: справедливая война может быть освободительной, захватнические войны все несправедливые.
Деление должно проводиться по одному основанию , т.е. нельзя в процессе деления заменять один признак, по которому проводилось деление, на другой. Нарушение этого правила приводит к нарушению предыдущего правила. “Транспорт делится на наземный, водный, воздушный, общественный, личный” - здесь в качестве основания деления первоначально берётся вид среды, в которой осуществляются перевозки, а затем - назначение транспорта.
Деление должно быть непрерывным , т.е., не закончив деления родового понятия, нельзя переходить к делению видовых понятий. Нарушение этого правила приводит к скачку в делении . Например: “Высшие растения делятся на травы, деревья и сосны”. Здесь очевиден скачок: сначала нужно закончить разделение рода высших растений на травы, деревья и кустарники, затем перейти к делению деревьев на хвойные и лиственные и лишь затем делить хвойные на сосны, ели, кедры и т.д. Нарушение этого правила приводит к тому, что некоторый вид ставится в один ряд с его родом.
Деление понятий следует отличать от мысленного расчленения предмета на части . Это совершенно разные операции, приводящие к разным результатам и преследующие разные цели. При мысленном расчленении предмета на части квартира делится на комнаты, кухню, коридор, туалет; автомобиль - на мотор, кузов, колёса и т.д. Но нельзя делить дома на жилые, нежилые и квартиры, а самолёты – на военные, гражданские, крылья и колёса. Такое смешение деления и мысленного расчленения приводит к путанице. Как и при ограничении понятия, при делении следует помнить, что в результате деления мы получаем виды некоторого рода и всё то , что можно сказать о роде, будет справедливо и для вида, например, всё то, что справедливо для автомобиля вообще, справедливо и для легкового автомобиля. В результате же расчленения мы получаем части предметов, но то, что можно сказать о предмете в целом, далеко не всегда верно для его отдельных частей. Например, можно сказать: “Автомобиль - не роскошь, а средство передвижения”, но выражение “Колесо - не роскошь, а средство передвижения” будет чушью.
Деление понятия – это интеллектуальная операция, которая тоже может быть предметом мысли, и как о предмете мысли мы о ней имеем понятие. И к этому понятию мы также можем применить логическую операцию “деление понятия”, т.е. понятие с именем “деление понятия” будем разбивать на виды в зависимости от основания деления. Если в качестве основания деления взять признак “число членов деления”, деление понятия может быть двух типов:
1) деление по видообразующему признаку;
2) дихотомическое деление.
Деление называется делением по видобразующему признаку , если количество членов деления больше двух. Соответственно число состояний основания деления также больше двух. Примером деления по видообразующему признаку может служить всё то же разбиение волосатых людей на блондинов, брюнетов, рыжих и шатенов.
Дихотомическое деление - это такое деление понятия, число членов деления которого равно двум (приставка “ди” означает “два”). Число состояний основания деления также равно двум. При этом одним состоянием является сам признак, служащий основанием деления, а другим состоянием – отрицание этого признака, т.е. признак с частицей “не”. Говоря иначе, членами дихотомического деления являются контрадикторные понятия. Примерами дихотомического деления может служить разделение всех людей на блондинов и не блондинов, деление всех веществ на органические и неорганические и т.д.
Если в качестве основания деления взять признак “число последовательно проведённых шагов деления”, то в этом случае можно различить одноступенчатое деление, когда из исходного понятия получают его виды и на этом останавливаются, и многоступенчатое деления, когда полученные члены деления делят ещё и ещё. Многоступенчатое деление называют классификацией . В свою очередь классификация бывает двух видов: естественная и вспомогательная.
Назначение естественной классификации состоит в распределении предметов по группам (классам) на основании их существенных признаков. Такая классификация отображает реальные различия между предметами, и на основании места, которое занимает предмет в классификации, можно судить о его свойствах. Примером естественной классификации может служить периодическая система химических элементов Д.И. Менделеева.
Назначение вспомогательной классификации состоит в распределении предметов по группам на основании их несущественных признаков. Примерами вспомогательной классификации могут служить алфавитные каталоги книг, списки фамилий, расположенных в алфавитном порядке.
Определение понятия
Определение – это логическая операция, раскрывающая содержание понятия и позволяющая отличить отображаемые им предметы от других предметов. Когда человек не знает каких-либо вещей, он спрашивает: что это такое ? В ответ он обычно получает определение. К примеру, на вопрос: “Что такое прямоугольник?”, можно получить ответ, что “прямоугольник - это плоская геометрическая фигура, ограниченная прямыми линиями, четырёхугольник с прямыми углами, у которого стороны попарно параллельны”. Это, конечно, определение, однако оно очень громоздко и практически неудобно, т.к. стремится перечислить все признаки, входящие в содержание определяемого понятия. Чтобы избежать этой ситуации, разработаны правила построения определений, которые позволяют отличить данный предмет от всех других, используя небольшое количество признаков. Эти правила построения определений зависят от вида используемого определения.
В первую очередь все определения можно разделить на остенсивные и вербальные.
Остенсивным называется определение, при котором задание значений слов происходит непосредственным указанием на предметы. Значение некоторых слов трудно, а порой и невозможно выразить иными словами, и в этом случае прибегают к помощи остенсивных определений. Что такое “красный цвет”? Если объяснять словами, то едва ли что-нибудь получится. В таких ситуациях следует просто указать пальцем: вот у этого предмета красный цвет. Все люди в детстве именно так и усваивают родной язык.
Вербальным называется определение, в котором указание на предмет осуществляется посредством других слов.
В свою очередь все вербальные определения можно разбить на два больших класса: явные и неявные.
Явные определения
Явным называется определение, в котором можно явно выделить два основных элемента: определяемое понятие и определяющее понятие.
Определяемое понятие (лат. definiendum - дефиниендум) - это понятие, содержание которого неизвестно.
Определяющее понятие (лат. definiens - дефиниенс) - это понятие или набор понятий, содержание которых известно.
Определяемое понятие и определяющее понятие обычно разделяются знаком “тире”.Пример: прямоугольник - это четырёхугольник с прямыми углами. В этом определении “прямоугольник” - определяемое понятие, а “четырёхугольник с прямыми углами” - определяющее понятие. В этом примере определение построено через род и видовое отличие . Это наиболее широко рапространённый способ построения определений. Суть его состоит в том, что в процессе определения сначала формулируем понятие с широким объёмом - родовое, а затем, добавляя признаки, ограничиваем объём родового понятия до нужного размера. В примере с прямоугольником родовым понятием является “четырёхугольник”, а ограничивающим признаком - “обладающий прямыми углами”. Сформулировать точное определение непросто. Чтобы определение было корректным, оно должно удовлетворять следующим требованиям.
Правила явного определения
Определение должно быть соразмерным , т.е. объём определяющего понятия должен быть равен объёму определяемого понятия. Нарушение этого правила приводит к следующим ошибкам.
Слишком широкое определение, когда объём определяющего понятия больше объёма определяемого понятия. Пример: лампа - источник света. К источникам света помимо ламп относятся солнце, свечи, поэтому объём понятия “источник света” больше объёма понятия “лампа”.
Слишком узкое определение, когда объём определяющего понятия меньше объёма определяемого понятия. Пример: треугольник - это плоская геометрическая фигура с тремя равными сторонами. Это определение исключает из числа треугольников разносторонние треугольники.
Одновременно - слишком узкое и широкое определение. Пример: бочка - это сосуд для хранения жидкости. С одной стороны, это слишком широкое определение, т.к. сосудом может быть и банка, и бутылка, и ведро. С другой стороны, это определение слишком узкое, т.к. помимо жидкостей в бочке можно хранить огурцы, капусту и другие твёрдые тела.
Определение не должно содержать в себе круга , т.е. понятия, входящие в определяющую часть, сами не должны определяться через определяемое понятие. Ошибка, получаемая в результате невыполнения этого правила называется “круг в определении” .Например, в определении “вращение - это движение вокруг оси” допущена ошибка круга, если ось будет определяться как прямая, вокруг которой происходит вращение. Частным случаем ошибки круга является тавтология - повторение в определяющей части самого определяемого понятия, хотя, может быть, в ином словесном выражении. Например, “фильтрование - процесс разделения с помощью фильтров”.
Определение должно быть точным и ясным . Точность - это характеристика понятия, объём которого хорошо известен, т.е. известно, какие предметы объём понятия в себя включает. Соответственно определение называется точным, если хорошо известны объёмы всех понятий, входящих в определяющую часть. Ясность - это характеристика понятия, содержание которого хорошо известно, т.е. известно, какие признаки составляют содержание понятия. Определение называется ясным, если хорошо известны содержания всех понятий, входящих в определяющую часть. Ошибка, встречающаяся при нарушении этого правила, - определение неизвестного через неизвестное . Пример: сепулькарии - это объекты, служащие для сепуления (Ст. Лем). Навряд ли кому-нибудь известно, что такое “сепуление”. (Помимо ошибки “определение неизвестного через неизвестное” здесь ещё и очевидная тавтология.)
Желательно, чтобы определение не было отрицательным , поскольку отрицательные определения содержат очень незначительную информацию. Много ли можно узнать из определения, что “самолёт - это не паровоз”? Отрицательные определения имеет смысл давать в тех случаях, когда родовое понятие к определяемому делится всего на два вида, одним из которых является определяемое понятие, а другим - контрадикторное к определяемому. Тогда, при отрицании контрадикторного понятия, получается достаточно точное и ясное определение требуемого понятия. Пример правомерного применения отрицательного определения: параллельные прямые - это прямые линии, лежащие в одной плоскости, которые не пересекаются. В данном случае родовым понятием является понятие “прямые линии, лежащие в одной плоскости”. Прямые линии, лежащие в одной плоскости, бывают всего двух типов - пересекающиеся и непересекающиеся. Отбрасывая в определении признак “пересекающиеся”, мы получаем необходимый объём определяемого понятия.
Когда встречается какое-либо явное определение, прежде всего, до проверки его по всем правилам, нужно задать себе вопрос: “Смогу ли я только на основании этого определения отличить определяемый предмет от всех других?”. Если смогу, то определение хорошее, если нет, то нужно смотреть, какое правило нарушено.
К явным определениям относятся и генетические определения. Название этого вида определения произошло от греческого слова genesis (генезис), что значит “происхождение”, “развитие”. Генетическое определение - это определение, в котором указывается такой способ происхождения определяемого предмета, который принадлежит только данному предмету и никакому другому. Пример: окружность - это кривая замкнутая линия на плоскости, образуемая движением точки В отрезка прямой АВ вокруг неподвижной точки А. В этом определении способ образования стоит на месте видового отличия.
Все определения можно разделить на реальные и номинальные .
Определение называется реальным , если цель его состоит в отличении предмета мысли, выражаемого понятием, от всех других предметов. Пример реального определения: “Квадрат – это прямоугольник с равными сторонами”. Этим определением мы отличаем квадрат от всех других прямоугольников.
Определение называется номинальным , если его цель состоит во введении нового имени (слова, обозначающего понятие). Номинальные определения - это соглашение о значениях тех или иных слов, которыми обозначаются предметы. Соответственно эти соглашения можно изменять. “Квадратом называется прямоугольник с равными сторонами” (1) - это номинальное определение, которым вводится в употребление термин “квадрат”. Если слово “квадрат” нам по каким-либо причинам не понравилось, мы, по договорённости, можем ввести другой термин - “стряклом называется прямоугольник с равными сторонами” (2). Для номинальных определений характерно присутствие в их составе слова “называется”.
Неявные определения
К неявным определениям относятся прежде всего контекстуальные определения. Название этого вида определений произошло от латинского слова contextus (контекстус), что означает “сцепление”, “соединение”, “связь”. Контекст
29-04-2015, 05:18