Оба предприятия могут внести одинаковый вклад в достижение представленной цели в рамках проекта
3
Слабое превосходство одного участника над другим
Есть некоторые основания предпочесть одно предприятие другому, но их нельзя считать неопровержимыми
5
Один существенно выгоднее другого (сильное превосходство)
Одно из предприятий обладает значительными конкурентными преимуществами
7
Очевидная конкурентоспособность участника
Имеются неопровержимые основания, чтобы предпочесть одно предприятие другому
9
Абсолютная значимость участника
Превосходство одного из предприятий столь очевидно, что не может вызвать ни малейшего сомнения
Значения 2, 4, 6, 8 соответствуют промежуточным суждениям и используются, когда выбор между двумя соседними нечетными числами вызывает затруднение.
При сравнении элемента с самим собой имеем равную значительность, поэтому главная диагональ матрицы должна состоять из единиц.
2) Нормализованная оценка вектора приоритетов . В математических терминах это вычисление главного собственного вектора, который после нормализации становится вектором приоритетов. Грубые оценки этого вектора могут быть получены следующими
четырьмя способами, которые представлены ниже в порядке увеличения точности оценок: 1. Суммировать элементы каждой строки и нормализовать делением каждой суммы на сумму всех элементов; сумма полученных результатов будет равна единице. Первый элемент результирующего вектора будет приоритетом первого объекта, второй – второго объекта и т. д.
2. Суммировать элементы каждого столбца и получить обратные величины этих сумм. Нормализовать их так, чтобы их сумма равнялась единице, разделить каждую обратную величину на сумму всех обратных величин.
3. Разделить элементы каждого столбца на сумму элементов этого столбца (нормализовать столбец), затем сложить элементы каждой полученной строки и разделить эту сумму на число элементов строки. Это – процесс усреднения по нормализованным столбцам.
4. Умножить n элементов каждой строки и извлечь корень n -й степени. Нормали-
зовать полученные числа.
В наших расчетах будем использовать 3-й способ.
Рассмотрим пример: посчитать вектор приоритетов для следующей матрицы попарных сравнений
| Критерии |
Стоимость поставки |
Наличие СМК |
Оценка качества образцов |
Время доставки |
Обеспечение сохранности продукции |
Широта ассортимента |
| Стоимость поставки |
1 |
1/4 |
1/5 |
1/3 |
2 |
6 |
| Наличие СМК |
4 |
1 |
1/3 |
3 |
4 |
8 |
| Оценка качества образцов |
5 |
3 |
1 |
4 |
5 |
9 |
| Время доставки |
3 |
1/3 |
1/4 |
1 |
3 |
7 |
| Обеспечение сохранности продукции |
1/2 |
1/2 |
1/5 |
1/3 |
1 |
6 |
| Широта ассортимента |
1/6 |
1/8 |
1/9 |
1/7 |
1/6 |
1 |
| Итого |
13,667 |
5,208 |
2,094 |
8,809 |
15,167 |
37 |
Разделив элементы каждого столбца на сумму элементов этого столбца, получим нормализованную матрицу:
| 0,0732 |
0,0480 |
0,0955 |
0,0378 |
0,1319 |
0,1622 |
| 0,2927 |
0,1920 |
0,1590 |
0,3406 |
0,2637 |
0,2162 |
| 0,3658 |
0,5760 |
0,4776 |
0,4541 |
0,3297 |
0,2432 |
| 0,2195 |
0,0639 |
0,1194 |
0,1135 |
0,1978 |
0,1892 |
| 0,0366 |
0,0960 |
0,0955 |
0,0378 |
0,0659 |
0,1622 |
| 0,0122 |
0,0240 |
0,0530 |
0,0162 |
0,0110 |
0,0270 |
Результаты усреднения по нормализованным столбцам:
| Сумма строк |
Вектор приоритетов |
| 0,5485 |
0,0914 |
| 1,4642 |
0,2440 |
| 2,4464 |
0,4077 |
| 0,9033 |
0,1506 |
| 0,4940 |
0,0823 |
| 0,1435 |
0,0239 |
3) Максимальное собственное значение (λmax ). Умножив матрицу попарных сравнений на полученный вектор приоритетов, получим новый вектор. Разделив первую компоненту этого вектора на первую компоненту оценки вектора решения, вторую компоненту нового вектора на вторую компоненту оценки вектора решения и т. д., определим еще один вектор. Разделив сумму компонент этого вектора на число компонент, найдем приближение к числу λmax , используемому для оценки согласованности, отражающей пропорциональность предпочтений. Чем ближе λmax к n , тем более согласован результат.
Для рассматриваемого примера имеем:
| Вектор приоритетов |
Новый вектор 1 |
Новый вектор 2 |
| 0,0914 |
0,5923 |
6,4787 |
| 0,244 |
1,7178 |
7,0392 |
| 0,4077 |
2,8261 |
6,9311 |
| 0,1506 |
1,0224 |
6,7910 |
| 0,0823 |
0,5252 |
6,3795 |
| 0,0239 |
0,1502 |
6,2812 |
Складываем числа в столбце Новый вектор 2 и получаем 39,9008. Таким образом, λmax = 39,9008/6 = 6,6501
4) Полученная матрица должна быть согласована. В общем случае, под согласованностью подразумевается то, что при наличии основного массива необработанных данных все другие данные логически могут быть получены из них.
Например, если объект А1 в 3 раза превосходит объект A2 и в 6 раз превосходит A3,
то A1=3A2 и A1=6A3. Следовательно, 3A2=6A3, или A2=2А3 и A3=1/2A2.
Известно, что согласованность положительной обратно-симметричной матрицы эквивалентна требованию равенства ее максимального собственного значения max λ с n . Можно также оценить отклонение от согласованности разностью max λ − n , разделенной на (n −1) . Заметим, что неравенство max λ ≥ n всегда верно.
Индекс согласованности – отклонение от согласованности, которое выражается формулой:
ИС = (λ max - n )/ ( n -1)
В рассматриваемом примере ИС = (6,6501-6)/5 = 0,13.
5) Случайный индекс – индекс согласованности сгенерированной случайным образом по шкале от 1 до 9 обратно-симметричной матрицы с соответствующими обратными величинами элементов. Рассчитывается по формуле:
СИ = М(ИС)
Значения СИ для матриц порядка от 1 до 15 представлены в Табл.№4.
Таблица №4.
Значения случайного индекса для матрицы попарных сравнений.
| Порядок матрицы |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| Значение СИ |
0,00 |
0,00 |
0,58 |
0,90 |
1,12 |
1,24 |
1,32 |
1,41 |
1,45 |
1,49 |
1,51 |
1,48 |
1,56 |
1,57 |
1,59 |
6) Отношение согласованности - отношение ИС к среднему СИ для матрицы того же порядка. Рассчитывается по формуле:
ОС = ИС/СИ
Для нашего примера ОС = 0,13/1,24 = 0,1049 (10,49%).
Значение ОС, меньшее или равное 0,10, считается приемлемым. В нашем случае ОС приемлемо.
После того, как составлены матрицы попарных сравнений для всех критериев и по каждому поставщику отдельно, проводим аддитивную свертку критериев.
Аддитивный метод свертки критериев предполагает построение интегрального критерия в виде простой или взвешенной суммы локальных критериев:
|
|
где ![]() – весовой коэффициент важности критерия, определяемый экспертным путем,
– весовой коэффициент важности критерия, определяемый экспертным путем,
![]() – рейтинговое число (интегральный критерий) j
-го предприятия.
– рейтинговое число (интегральный критерий) j
-го предприятия.
Таким образом, метод анализа иерархий включает в себя следующие четыре этапа:
Этап 1 . Построение соответствующей иерархии задачи принятия решений.
Этап 2 . Попарное сравнение всех элементов иерархии.
Этап 3 . Устранение несогласованности матриц попарных сравнений (если это необходимо).
Этап 4 . Математическая обработка полученной от ЛПР информации.
Для упрощения процедуры расчетов показателей при использовании метода анализа иерархий будем использовать возможности и диалоговые окна программной системы “MPRIORITY 1.0”.
3.3.2. Использование программной системы “MPRIORITY 1.0” в методе анализа иерархий .
Систему “MPRIORITY” отличает диалоговый интерфейс, адаптированный под особенности метода анализа иерархий и восприятие пользователя. Программа содержит диалоговые средства, позволяющие получать наиболее полную информацию о проведенных попарных сравнениях и устранять возможные несогласованности в матрицах попарных сравнений.
Использование присутствущего в программной системе механизма шаблонов (шаблон – готовая иерархия для одной из задач принятия решений) позволяет пользователю адаптировать программную систему под область своей деятельности.
Представим основные этапы методы анализа иерархий с помощью диалоговых окон программы.
Построение иерархии представлено на рис.1. Матрица попарных сравнений определяется через диалоговое окно качественной шкалы (рис.2).
Установить интенсивность взаимодействия между элементами иерархии или силу, с которой различные элементы одного уровня иерархии влияют на элементы предшествующего уровня можно с помощью матрицы попарных сравнений (рис.3).
После проведения попарных сравнений полученную матрицу можно проверить на согласованность (рис.4).
Следует отметить, что сокращенные наименования частных критериев, целей и альтернатив в программе “MPRIORITY 1.0” всегда можно раскрыть, используя “Комментарии” к элементам иерархии (рис .5).
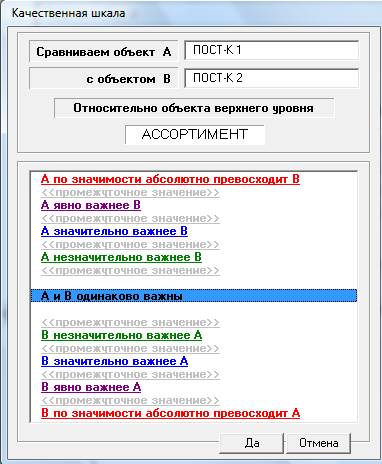
Рис.2. Диалоговое окно “MPRIORITY 1.0” качественной шкалы МАИ.
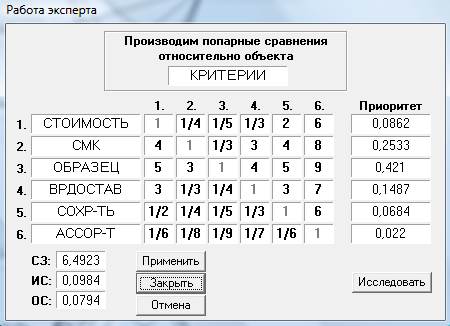
Рис.3. Таблица попарных сравнений для иерархии на рис.1.
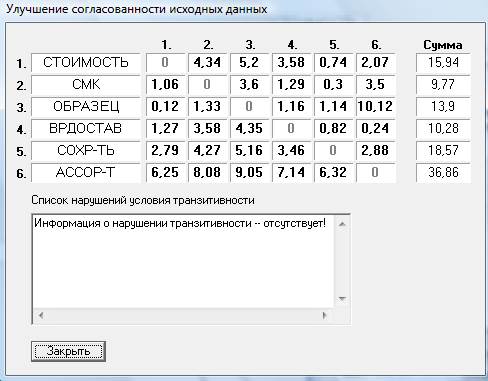
Рис.4. Диалоговое окно согласованности данных.
Рис.5. Диалоговое окно “Редактирование элемента”.
На рис. 6. представлено диалоговое окно, отражающее итоговый результат проведенных сравнений (претенденты расположены (ранжированы) в порядке уменьшения их значимости для фирмы).
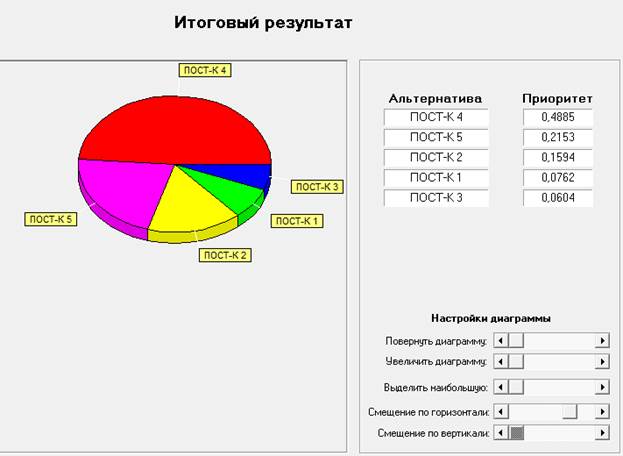
Рис.6. Диалоговое окно итогового результата проведенных сравнений.
Таким образом, в следующем разделе проведем расчеты по методу анализа иерархий с помощью программы “MPRIORITY 1.0” для выбора наилучшего поставщика.
IV. Выбор наилучшего поставщика с помощью метода анализа иерархий.
Для начала необходимо поставить задачу, которую необходимо будет решить в данном разделе.
Исходные условия : предприятию по производству косметической продукции среднего уровня в г.Москва необходимо выбрать нового поставщика жидких отдушек 55 различных видов. Отдушки должны быть по 11 направлениям аромата (морское, травяное, цветочное, фантазийное, фруктовое, шоколадно-молочное, древесное, ванильное, медово-кофейное, цитрусовое, хвойное) и 5 направлениям области применения (кремы, бальзамы, гели, маски и скрабы, лосьоны). Основные особенности сырья: жидкое, хранится при комнатной температуре, в темном помещении, предполагает вакуумную упаковку. Планируется закупить по 5 кг каждого вида сырья, итого получается 275 кг. Имеется возможность самостоятельной отгрузки и транспортировки сырья.
Было отобрано 5 потенциальных новых поставщиков:
1. ООО «РосКосметика» - производитель отдушек для косметики и бытовой химии. Месторасположение: Украина, г.Николаев.(Поставщик 1).
2. Ариэль Космет – дистрибьютер химического сырья для производства косметических препаратов, парфюмерии и средств бытовой химии из Германии, Франции, Голландии и Нидерландов. Месторасположение: Московская обл., Люберецкий р-н, г.Котельники. (Поставщик 2).
3. ООО «Флоресанс-Парфюм» - официальный дистрибьютер французской фирмы «Floressence». Основными направлениями деятельности являются реализация композиций, отдушек, эфирных масел и душистых веществ для производства парфюмерно-косметических изделий и товаров бытовой химии. Месторасположение: Украина, г.Киев. (Поставщик 3).
4. ООО «Тереза Интер» - дистрибьютер французской фирмы «РЕЙНО и ФИС», а также производитель парфюмерных композиций-баз и отдушек для всех видов парфюмерно-косметической продукции и бытовой химии. Месторасположение: г.Москва. (Поставщик 4).
5. ЗАО «Акжера-Ароматика» - производитель сырья и ингредиентов для пищевой и косметической промышленности. Месторасположение: г.Москва. (Поставщик 5).
Оценку поставщиков будем проводить по 6 основным критериям :
1) Стоимость поставки.
2) Наличие системы менеджмента качества (СМК).
3) Оценка качества пробных образцов закупок.
4) Продолжительность доставки.
5) Обеспечение сохранности продукции в процессе отгрузки и транспортировки.
6) Широта предлагаемого ассортимента.
Иерархия целей для нашей задачи представлена на рис.1.
Для составления матрицы попарных сравнений по критериям будем использовать результаты оценки каждого критерия группой из 5 экспертов.
4.1. Экспертная оценка основных критериев выбора поставщиков.
Пяти экспертам в области жидких отдушек для производства косметической продукции предложено оценить по 5-бальной шкале важность каждого критерия. 1б – самая низкая степень важности, 5б – самая высокая степень важности.
Результаты экспертных оценок представлены в Табл.№5.
Таблица №5.
Экспертная оценка критериев выбора поставщиков.
| Критерии |
Эксперт 1 |
Эксперт 2 |
Эксперт 3 |
Эксперт 4 |
Эксперт 5 |
Итого |
| Стоимость поставки |
4 |
3 |
3 |
5 |
5 |
20 |
| Наличие СМК |
5 |
4 |
5 |
5 |
3 |
22 |
| Оценка качества образцов |
5 |
3 |
5 |
5 |
5 |
23 |
| Время доставки |
4 |
5 |
4 |
3 |
5 |
21 |
| Обеспечение сохранности продукции |
5 |
3 |
4 |
4 |
4 |
20 |
| Широта ассортимента |
3 |
5 |
3 |
2 |
3 |
16 |
Разницу в итоговых значениях обозначим Δ. В зависимости от значения Δ будем выставлять ранги важности (Табл.№6).
Таблица №6.
Определение рангов важности для Δ.
| Δ |
Ранг важности |
| 0 |
2 |
| 1 |
3 |
| 2 |
4 |
| 3 |
5 |
| 4 |
6 |
| 5 |
7 |
| 6 |
8 |
| 7 и более |
9 |
На основании вышеописанных данных составим матрицу попарных сравнений основных критериев (Табл.№7).
Таблица №7.
Матрица попарных сравнений критериев оценки поставщиков.
| Критерии |
Стоимость поставки |
Наличие СМК |
Оценка качества образцов |
Время доставки |
Обеспечение сохранности продукции |

 ,
,