При использовании методов, описанных выше, необходимо проводить дополнительные исследования для различения случайного блуждания, хемотаксиса или хемокинеза. Такие методы исследования не дают возможности изучать отдельные клетки во время движения.
В 1953 году Харрис впервые использовал автоматический метод съемки движущихся нейтрофилов. Этот метод был использован в клинических исследованиях.
Полностью автоматизированные методы появились, когда были решены проблемы оптического выделения объектов и были созданы программы слежения за движущимися клетками (Туманов и соавт. 1990). В исследовании подвижности нейтрофилов важен выбор межкадрового интервала. В экспериментах (Hartoman R. S. el al 1994), средняя скорость движения при интервалах регистрации 4 сек. была 17 мкм/мин., а при интервалах 36 сек, составляла 9.9 мкм/мин. Отличие связано с тем, что размер нейтрофила составляет 10 мкм, а время нужное на перемещение равное клеточному диаметру приблизительно равно 1-1.5 минут. Поэтому для оценки внешнего движения используют 1 минутный межкадровый интервал, нейтрофилы за этот интервал времени перемещаются в среднем на величину клеточного диаметра. Такая регистрация позволяет оценить воздействие химических и физических факторов на подвижность нейтрофилов, проводить сравнение в норме и патологии.
Регистрация внутреннего движения используется для более подробного исследования изменений подвижности. Для этого выбирается межкадровый интервал такой, чтобы при непрерывном измерении перемещение центра массы клетки, связанное с изменением формы клетки за время межкадрового интервала не превышало клеточного диаметра (Hartman R. S. Lau K. Chou. W. Coates T. D. 1994).
Анализ траекторий случайного блуждания клеток, которые регистрируют с интервалом 2 сек. показывает, что поведение клеток отличается на малых и больших временах наблюдения. По степени корреляции разделяют два вида траектории движения:
1. Персистентное движение – клетка некоторое время пытается сохранить величину и направление движения.
2. Диффузионное движение – связано с внутренними процессами в клетке стремящимися изменить направление движения клетки.
Среднее время перехода между этими двумя формами движения называется характерным временем или временем персистентного движения (Tranquillo R.T. at al 1988).
Движение нейтрофилов изучали на покровных стеклах. Движение клеток происходит по определенной траектории, у каждой клетки она своя. Форма траекторий разнообразна, от плотного клубка до расплетенных нитей. Нейтрофилы бывают: медленные, средние и быстрые. Медленные – это клетки, которые вытягивают ламеллоподии в разные стороны, но в результате отсутствия скоординированного двигательного акта они стоят на месте или движутся но очень медленно. Средние клетки имеют траекторию более запутанную в виде плотного клубка из-за того, что они больше стоят на месте и углы поворотов у них больше. Быстрые клетки имеют меньшие углы поворотов и меньше времени стоят на месте, следовательно, их траектория более прямая. Такой вывод был сделан по произвольно выбранным клеткам. Время пребывания в фазе активности и углы поворотов определяются внутренней программой клетки.
Подвижность нейтрофилов может служить показателем тяжести состояния больных с раневой инфекцией.
Табл. 1 Средняя скорость движения и процентный состав нейтрофилов в группах здоровых доноров и больных с раневой инфекцией.
ГРУППЫ |
СКОРОСТЬ мкм/мин |
МЕДЛЕННЫЕ % |
СРЕДНИЕ% |
БЫСТРЫЕ % |
| ЗДОРОВЫЕ |
8.8 ± 0.2 |
16 |
28 |
56 |
| СР. ТЯЖЕСТИ |
6.5 ± 0.3 |
27 |
34 |
39 |
| ТЯЖЕЛЫЕ |
3.3 ± 0.3 |
58 |
27 |
15 |
У тяжелых больных средние скорости нейтрофилов распределены в диапазоне от 0 до 6 мкм/мин. Такой широкий диапазон средних скоростей из-за того, что больные подвергаются интенсивному лечению (операции, антибиотикотерапия). У больных средней тяжести, скорости распределены в области от 4.5-9 мкм/мин. Ухудшение состояния больного происходит из-за уменьшения клеток в популяции. При тяжелом состоянии средняя скорость в популяции ниже 3 мкм/мин, а скорость 5-6 мкм/сек говорит о том, что состояние средней тяжести.
Нарушение подвижности нейтрофилов было обнаружено у ожоговых больных и больных с острой пищевой токсикоинфекцией. В каждой группе было исследовано по 5 больных. В группу ожоговых больных входили тяжелые больные с площадью ожогов 50% поверхности тела. Группу с острой пищевой токсикоинфекцией составляли больные с тяжелой сальмонеллезной эндотоксимией. У этих больных интоксикация приводит к сильному угнетению подвижности нейтрофилов.
Табл. 2 Скорость движения и процентный состав неподвижных, медленных и быстрых нейтрофилов у ожоговых больных и больных с острой пищевой токсикоинфекцией.
| Больные |
Ожоги |
Пищевая токсикоинфекция |
| N = 5 |
Скор. % состав мкм/мин м:с:б |
Скор. % состав мкм/мин м:с:б |
| СРЕДНИЕ |
3.2 62:24:14 |
2.1 75:19:6 |
| ОШ. СРЕДНЯЯ |
0.4 |
0.5 |
Бактерии способны выделять хемоаттрактанты, которые притягивают нейтрофилы в зону инвазии (способность возбудителей проникать и распространяться в организме). Бактериальные хемоаттрактанты типа формил – пептида при больших концентрациях проявляют эффект «западни» угнетая движение нейтрофилов.
Алгоритм работы модели клетки
В поле зрения микроскопа клетка движется по случайной траектории. Из начального положения клетка может перемещаться на случайное расстояние в отрезке от 0 до rmax , под случайным углом от 0 до ±1800 .
Случайный шаг характеризуется распределением:
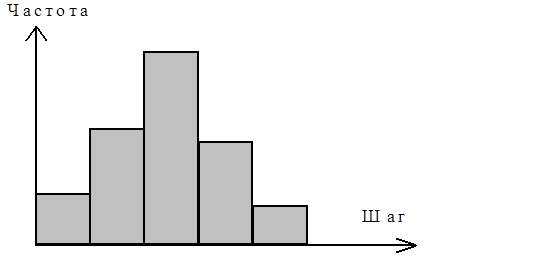
рис. 3 Распределение (частота встречаемости) шагов, на которые клетка перемещается за выбранный промежуток времени (1 минута).
Клетка во время движения может менять как шаги, так и углы поворотов, от 0 до 1800 . Углы меняются по отношению к предыдущему направлению клетки.
Случайные углы поворота нейтрофилов характеризуются распределением:
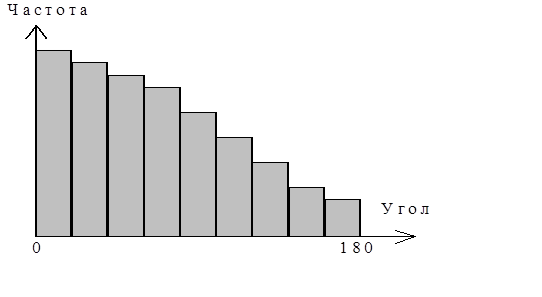
рис. 4 Распределение углов поворотов при случайном движении. Углы распределены от 0 до 1800, знак угла считается равновероятным.
Из распределения углов поворота видно, что нулевой угол встречается чаще, следовательно, он наиболее вероятен, а угол 1800 наименее вероятен. Из этого следует, что клетка при движении сохраняет свое направление. Углы поворотов распределены от 0 до 1800 , при этом знак угла считается равновероятным (вправо или влево). В соответствии с такой гипотезой строится алгоритм модели движения клетки.
Нейтрофилы разделены на три типа: быстрые, средние и медленные. Три типа клеток различаются между собой по максимально возможному шагу в единичном акте движения. Для медленных клеток эта величина составляет 3 мкм (величина меньше размера клетки). Для средних клеток – 10 мкм (величина, немного превышающая размер клетки). Для быстрых клеток составляет 30 мкм.
Вычисление координат клетки
Координаты каждой последующей клетки вычисляются из предыдущего. Программа генерирует три случайных числа в соответствии с заданными распределениями (для каждого вида нейтрофилов своё распределение)
ri - случайный шаг.
ji - угол поворота.
signi - направление поворота.
Вычисляем угол по отношению к оси 0X.
F i = F i-1 + signi ´ j i
xi = xi-1 + ri cos F i
yi = yi-1 + ri sin F i
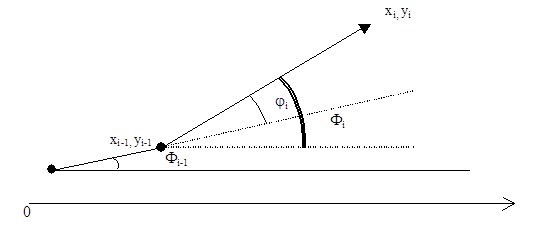
рис. 5 Движение нейтрофила по случайной траектории.
Во время работы модели вычисляется на каждом шаге пройденный клеткой путь и строится график зависимости пройденного пути от времени.
Генерация случайных чисел с заданным распределением (Монте-Карло)
Пусть величина y принимает значения y1 ,y2 ,…,yn , с вероятностями p1 ,p2 ,…,pn . Сумма вероятностей p1 +p2 +…+pn =1 . Разобьем отрезок [0,1] на отрезки p1 ,p2 ,…,pn .
Алгоритмические языки программирования имеют генератор равномерно распределенных псевдослучайных чисел. Если псевдослучайное число x i , равномерно распределенное на отрезке [0,1] мы будем «бросать» на отрезок, то он будет попадать в интервалы p1 ,p2 ,…,pn , с частотой, пропорциональной длине этих интервалов. Из этого следует, что числа y1 ,y2 ,…,yn будут появляться в соответствии с вероятностями p1 ,p2 ,…,pn .
Язык Pascal генерирует целые положительные псевдослучайные числа, распределённые в заданном интервале x:=random(100) . Такая процедура будет генерировать числа, равномерно распределенные в интервале [0,100].
В данной программе вероятность измерялась в процентах. Все вероятности измерялись в целых числах, что превышало точность измерений. Таким образом были построены генераторы случайных шагов, углов поворота, случайных изменений площади, случайных коэффициентов адгезии (прилипания). Единственное исключение составляло явление поворота. Если генерируемая величина была меньше 50, угол поворота положителен, и если величина больше, либо равняется 50, то угол поворота отрицателен. Для каждой вычисляемой величины, генерировалась отдельная случайная величина y , поскольку величины ri ji считаются независимыми.
Алгоритм реализации конкретного распределения. На рис. 5 показана гистограмма (дифференциальное распределение) частоты встречаемости шагов клетки за выбранный интервал (интервал времени между измерениями).
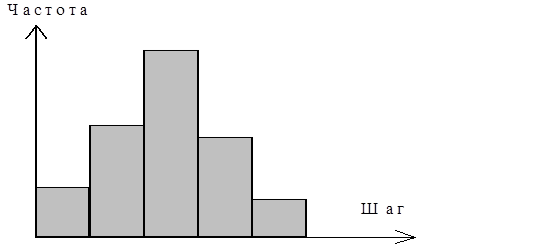
рис. 6 Дифференциальное распределение.
Всё время работы алгоритма подсчитывается частота встречаемости каждого шага по всей популяции, за все время конкретного расчета (120 шагов по 1ой минуте). Полученные результаты выводились в виде гистограмм минутных сдвигов. При построении гистограмм, все теоретические клетки «смешивались в кучу», хотя в программе заведомо заданно, что клетки относятся к разным типам.
Исходя из дифференциального распределения, строим другую гистограмму.

рис. 7 Куммулятивная гистограмма.
Полученная гистограмма называется куммулятивной гистограммой (интегральное распределение). Генерируемая процедура паскаля равномерно распределенное случайное число y обязательно попадает в один из интервалов от p1 до p5 . При его попадании в интервал pi , выбираем шаг ri , который и будет использоваться в вычислении следующего положения клетки. Очевидно, что при длительной работе алгоритма, доля шагов ri будет пропорциональна вероятности pi . Аналогичным образом вычисляется на каждом шаге все остальные параметры движения клеток.
Программная реализация алгоритма
В программе для случайной величины предусмотрена следующая таблица:
Табл. 3
| № |
Значение шага |
Частота наблюдений |
Частота в % |
Куммулятивная гистограмма |
| 1 |
R1 |
N1 |
Cent 1 |
Cent 1 |
| 2 |
R2 |
N2 |
Cent 2 |
Cent 1 + Cent 2 |
| : |
: |
: |
: |
: |
| 10 |
R10 |
N10 |
Cent 10 |
å Cent |
Величины шагов, углы площади разбиты равномерно от 0 до максимального значения. Значение, больше максимального в эксперименте не встречается. Значения частоты наблюдений обозначают частоту встречаемости этих шагов в произвольном измерении. В принципе, сумма частот встречаемости должна составлять 1 или 100%. Однако при реальном моделировании, поле приходится описывать в виде приблизительного распределения. При этом мы можем увеличивать или уменьшать частоты появления отдельных шагов. Если при этом заботиться о том, что суммы всех частот должна составлять 100%, то это сильно затруднит просмотр всех вариантов. После подгонки формы приблизительного распределения, программа нормализует сумму частот к 100% по формуле
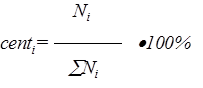
Таким образом формируется 3-й столбец таблицы. После формирования 3-го столбца таблицы, программа формирует 4-й столбец, представляющий собой куммулятивное распределение.
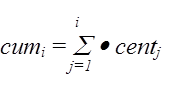
В программе полученное равномерно распределенное число y последовательно начиная с 1-го сравнивается с числами четвертого столбца. При этом номер числа последовательно наращивается. Как только y превысит очевидное число из 4-го столбца, процедура заканчивает свою работу. Номер последнего числа считается номером избранного числа, значение которого извлекается из первого столбца.
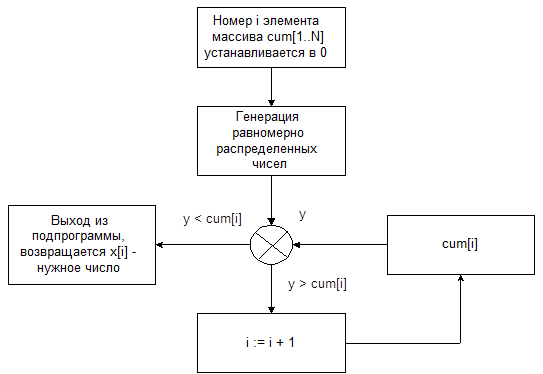
рис. 8 Алгоритм генерации случайного числа, заданным распределением.
Этому алгоритму соответствует следующая процедура:
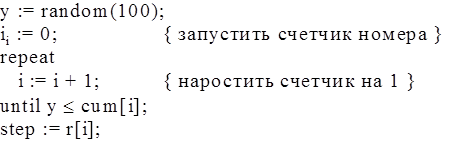
Процедура редактирования распределений
Любая программа подразумевает обеспечение «экранного сервиса». На экране должны возникать таблицы исходных данных, которые удобно редактировать. Для этого должно быть предусмотрено создание в программе текстового файла, в котором изображается экранная таблица со специальными символами. Символы обозначают будущие места, в которых будут стоять исходные данные. Заранее оговариваются специальные символы.
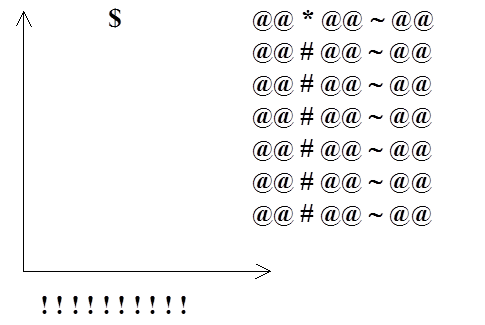
рис. 9 Распределение служебных мест на экране для редактирования параметров измерения.
Специальные символы, которые указывают местоположение будущих значений.
| @ |
- место переключения фона. |
| # |
- место, где будет выведено значение параметров. |
| ~ |
- место, где будут выводиться частоты. |
| ! |
- место, где строятся столбцы гистограммы. |
| * |
- либо шаг, либо угол. Название параметра. |
| $ |
- место, в которое выводится тип клетки. (slow, medium, fast). |
|
|
Процедура формирования экрана работает следующим образом. Текстовый файл считывает символ за символом. Если считанный символ не входит в список специальных, он просто выводится на экран. Таким образом, на экран могут выводиться любые комментарии, например: инструкции по редактированию таблицы. При выводе всех символов, подсчитывается номер строки и номер позиции в строке. Номер позиции в строке задаётся в начале, равный единице. И наращивается с введением каждого нового символа до появления символа eoln (end of line - конец строки). После увеличивается на единицу счетчик номера строк и сбрасывается в единицу счетчик номера позиции. Работа процедуры заканчивается eof (end of file - конец файла).
Измерение среднеквадратичного отклонения
На рис.10 показана траектория клетки.
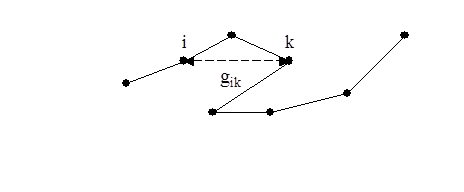
рис. 10 Траектория движения клетки.
Вычисляются квадраты расстояния gik , т. е. между i-тым и k-тым положениями клетки. Для каждой заданной разници n = k – i усредняются вдоль траектории все квадраты gik .
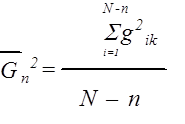
Результаты исследования
При исследовании движения популяции клеток было обнаружено, что нейтрофилы, выделенные из одной и той же пробы, движутся с различными скоростями. Этот факт может объясняться многими причинами, главные из которых, по видимому, является возраст клеток, но мы не будем подробно изучать зависимость клеток от возраста.
Экспериментатор, условно разделил клетки на медленные, средние и быстрые. Количество таких клеток в популяции составляет 15 : 30 : 55. При моделировании популяции мы исходим из этого соотношения.
Программа генерировала случайное количество быстрых, средних и медленных «клеток», в среднем дающих экспериментальное соотношение. При моделировании клеток в популяции, экспериментальный шаг (шаг за единицу времени) случаен. Распределение этих шагов, задается распределением, показанным на рис. 11 .
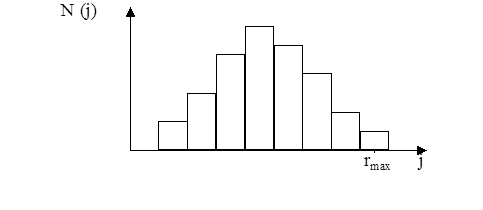
рис. 11 Распределение элементарных шагов за единицу времени (1 минута).
Описание распределения было выбрано произвольно, так, чтобы оно напоминало экспериментальное распределение. Полный интервал возможных случайных шагов от 0 до rmax для каждого типа клеток (медленные, средние, быстрые) разбивался на 10 шагов. Зависимость частоты встречаемости каждого шага ri от величины шага гистограммы описывается формулой:
N( j ) =100 · sin ( p · j/10)
j £ 10
Таким образом, распределение элементарных шагов для всех типов клеток предполагается одинаковым. Отличается только величина возможного шага для данного типа клеток. Максимально возможный шаг составляет:
Для медленных — 3 мкм.
Для средних — 10 мкм.
Для быстрых — 30 мкм.
Распределение углов поворотов на каждом шаге для всех типов так же предполагается одинаковым.
![]()
Диапазон углов от 0 до 1800 разбивался на 10 интервалов. Таким образом, каждый шаг гистограммы соответствовал углу в 180 .
Измерение пройденного пути
Наиболее естественный показатель движения клетки в эксперименте, считается пройденный путь. На рис. 12
можно наблюдать нарастание пройденного
8-09-2015, 21:04
