 Днепропетровский Государственный Технический Университет Железнодорожного Транспорта.
Днепропетровский Государственный Технический Университет Железнодорожного Транспорта.
Кафедра : «Теплотехника»
ДОМАШНЕЕ ЗАДАНИЕ
На тему : «Прямой цикл Карно» ,
«Тепловая изоляция»
Выполнил :
студент 427 группы
Астраханцев Дмитрий
Принял :
Доц. Арестов А.П.
Днепропетровск 1998
Прямой цикл Карно.
Как известно, все тепловые двигатели, превращающие тепловую энергию в механическую, работают по круговым циклам или термодинамическим циклам – идеальный цикл теплового двигателя (прямой цикл Карно) и цикл холодильной машины (обратный цикл Карно).
Рассмотрим прямой цикл Карно. Для этой цели возьмем идеальную систему, состоящую из горячего источника тепла, рабочего тела и окружающей среды. Параметры источника тепла Тг, Sг, температура окружающей среды Т0 . Рабочее тело в конечном итоге не совершает работы за счет своей собственной энергии. До начала работы и после ее завершения все параметры рабочего тела и его полная энергия остаются в точности теми же самыми. Иначе говоря, рабочее тело изменяет свои параметры по какому-то циклу, возвращаясь каждый раз в первоначальное состояние. Суммарная работа окружающей среды над телом равна нулю; никаких потерь работы нет; энтропия системы остается неизменной (Sc=0); все процессы обратимые.
При отдаче горячим источником рабочему телу тепла dQ1 тело произведет суммарную работу dL и, для того чтобы вернутся в первоначальное состояние, отдаст окружающей среде тепло dQ2. При этом энтропия горячего источника уменьшится на величину dSг = dQ1 /T1 , а энтропия холодного источника возрастет на dSx = dQ2 /T0 .
Поскольку согласно второму закону термодинамики энтропия рассматриваемой изолированной системы уменьшаться не может, то при dSг < 0 всегда будет dSx > 0, а следовательно, и dQ2 > 0. Значит, совершая работу с помощью циклов, тепло должно не только подводится, но и обязательно отводиться.
В идеальном случае, когда достигается максимальная работа, dSг + dSx = 0 и величина dQ2 является минимальной. Таким образом,
-dQ1 /Tг = dQ2 min /T0 ,
или
dQ2 min = T0 dSг ,
где dSг берется по абсолютной величине (без отрицательного знака), т.е. dSг = dQ1 /Tг.
Согласно первому закону термодинамики, всегда
dL = dQ1 – dQ2 ,
dLmax = dQ1 – dQ2 min ,
или
dLmax = dQ1 – T0 dSг,
т.е. максимальная работа цикла за счет тепла Q
Lmax = Q1 – T0 (Sг2 – Sг1 ),
где (Sг2 – Sг1 ) – абсолютна величина уменьшения энтропии горячего источника, вызванная отдачей тепла Q1 .
Очевидно, что эта формула будет справедлива независимо от того, меняется или не меняется температура Тг горячего источника. Обязательными условиями ее справедливости являются только постоянство температуры окружающей среды и обратимость всех процессов цикла. Максимальная полезная работа, которая может быть совершена в идеальном (обратимом) тепловом двигателе, оказывается абсолютно одинаковой, будет ли этот двигатель работать по какому-либо обратимому циклу или в нем будут совершаться любые разомкнутые процессы.
Максимальная доля тепла, которая может быть превращена в работу, обычно выражается через отношение Lmax /Q1 , называемое термическим к. п. д. теплового двигателя :
t = Lmax /Q1 = (Q1 – Q2min )/Q1 .
При постоянных температурах горячего Тг и холодного Т0 источников, учитывая предыдущие формулы максимальный термический к. п. д. теплового двигателя :
t =1 – Т0 /Тг.
Можно доказать, что значение максимальной работы, а следовательно, и максимальный термический к. п. д. для случая источников тепла постоянной температуры достигается в обратимом прямом цикле Карно, состоящем из двух изотерм и двух адиабат :
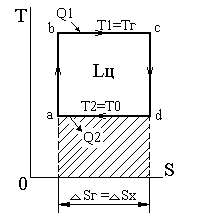 |
Условия построения прямого цикла Карно следующие :
1) Поскольку подвод тепла обратимый, то при Тг = const температура тела Т1 на протяжении всего процесса подвода тепла должна быть равной Тг и оставаться постоянной : Т1 = Тг=const;
2) Так как и отвод тепла должен быть обязательно обратимым, то и температура Т2 тела в процессе отвода тепла также должна быть равна Т0 и оставаться постоянной : Т2 = Т0 =const;
3) Поскольку в других процессах тепло не должно подводиться и отводиться, то замыкание цикла может осуществляться только процессами с постоянной энтропией (S = const), следовательно, должно быть : Sa = Sb и Sc = Sd .
В изображенном на рисунке цикле изоэнтропа ab – процесс адиабатического сжатия рабочего тела; изотерма bc – процесс подвода тепла Q1; изоэнтропа cd – процесс адиабатического расширения рабочего тела; изотерма da – процесс отвода тепла Q2 к холодному источнику (окружающей среде). Одновременно изотермы bc и da - соответственно процессы отвода тепла от горячего источника и подвода тепла к холодному источнику. В этом, как и в любом другом, обратимом цикле значения изменения энтропии горячего и холодного источников равны между собой по абсолютной величине и имеют обратные знаки, т.е.
Sг =Sx
Конечное изменение энтропии Sт рабочего тела, совершающего замкнутый процесс, будет равен нулю. Приращение энтропии системы, равное алгебраической сумме энтропии всех тел рассматриваемой системы (обеих источников тепла и рабочего тела), также равно нулю :
Sc = Si = Sг +Sx +Sт = 0.
Этим подтверждается, что цикл Карно действительно дает максимальную работу.
Из рисунка находим :
Q1 = TгSг = Т1 Sг ;
Q2 = T0 Sx = T2 Sг,
Отсюда
Lц = Q1 – Q2 = (T1 – T2 )Sг.
С учетом того, что Sг = Q1 /T1 , получим
Lц = Q [(T1 -T2 )/T1 ].
Термический к. п. д. этого цикла
t = Lц /Q1 = 1 – T2/T1 = t мах
С помощью прямого цикла Карно можно доказать, что отводимое к холодному источнику тепло Q2 min не является потерей энергии, а представляет собой тот «балласт», ту непревратимую часть энергии, которая в любой момент, без затраты какой-либо дополнительной работы, может быть отнята от холодного источника и возвращена горячему.
Здесь следует заметить, что осуществляя обратный цикл Карно, можно, затратив работу Lц , получить и отдать горячему источнику тепла Q1 ровно столько, сколько было от него получено в прямом цикле, а от холодного источника будет отобрано в точности такое же количества тепла Q2 min , сколько ему было отдано в прямом цикле.
ТЕПЛОВАЯ ИЗОЛЯЦИЯ.
Теплоизоляция – это защита зданий, промышленных установок (или отдельных их узлов) от нежелательного теплового обмена с окружающей средой. Так, например, в строительстве и теплоэнергетике теплоизоляция необходима для уменьшения тепловых потерь в окружающую среду, в холодильной и криогенной технике – для защиты аппаратуры от притока тепла извне.
Теплоизоляция обеспечивается устройством специальных заграждений, выполняемых из теплоизоляционных материалов (в виде оболочек, покрытий и т.п.) и затрудняющих теплопередачу; сами эти теплозащитные средства также называются теплоизоляцией.
При преимущественно конвективном теплообмене для теплоизоляции используются ограждения, содержащие слои материала, непроницаемого для воздуха; при лучистом теплообмене – конструкции из материалов, отражающих тепловое излучение (например из фольги, металлизированной лавсановой пленки); при теплопроводности (основной механизм переноса тепла) – материалы с развитой пористой структурой.
Эффективность теплоизоляции при переносе тепла теплопроводностью определяется термическим сопротивлением ( R) изолирующей конструкции R = / , где - толщина слоя изолирующего материала, - его коэффициент теплопроводности.
Повышение эффективности теплопроводности достигается применением высокопористых материалов и устройством многослойных конструкций с воздушными прослойками.
В тепловых промышленных установках теплоизоляция обеспечивает значительную экономию топлива, способствует увеличению мощности тепловых агрегатов и повышению их КПД, интенсификации технологических процессов, снижению расходов основных материалов. Экономическая эффективность теплоизоляции в промышленности часто
оценивается коэффициентом сбережения тепла
Где Q1 – потери тепла без теплоизоляции, а Q2 – с теплоизоляцией.
Задача теплоизоляции зданий – снизить потери тепла в холодный период года и обеспечить постоянство температуры в помещениях в течении суток при колебаниях температуры наружного воздуха. Применяя для теплоизоляции эффективные теплоизоляционные материалы, можно существенно уменьшить толщину и снизить массу ограждающих конструкций и, т.о. сократить расход основных стройматериалов.
Теплоизоляция – необходимый элемент конструкции транспортных средств (судов, ж.д. вагонов, самолетов и т.д.), в которых роль теплозащиты определяется их назначением : для средств пассажирского транспорта – требованием поддержания комфортных микроклиматических условий в салонах; для грузового – обеспечение заданной температуры при минимальных энергетических затратах. К эффективности теплоизоляции на транспорте предъявляются повышенные требования в связи с ограничением массы и объема ограждающих конструкций транспортных средств.
Материалы и изделия, применяемые для теплоизоляции называются теплоизоляционными. Теплоизоляционные материалы характеризуются низкой теплопроводностью (коэффициент теплопроводности не более 0.2 Вт/м*К), высокой пористостью, незначительной объемной массой и прочностью (предел прочности при сжатии 0.05-2.5 МН/м2 ).
Основной показатель качества теплоизоляторов – коэффициент теплопроводности. Он является физическим параметром вещества и в общем случае зависит от температуры, давления и рода вещества. В большинстве случаев коэффициент теплопроводности определяется экспериментально с помощью различных методов. На рисунке показаны примерные значения коэффициента теплопроводности для
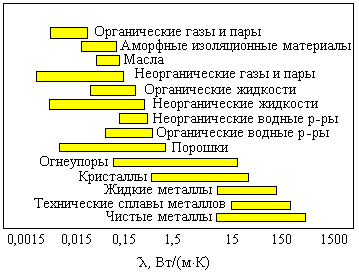 |
различных веществ :
Так как тела могут иметь различную температуру, а при наличии теплообмена и в самом деле температура будет распределена неравномерно, то в первую очередь важно знать зависимость коэффициента теплопроводности от температуры. Опыты показывают, что для многих материалов с достаточной для практики точностью зависимость коэффициента теплопроводности от температуры можно принять линейной :
=0 [1+b(t-t0 )],
где 0 – значение коэффициента теплопроводности при температуре t0 ; b – постоянная, определяемая опытным путем.
Коэффициент теплопроводности газов. Согласно кинетической теории перенос тепла в газах при обычных давлении и температуре определяется переносом кинетической энергии молекулярного движения в результате хаотического движения и столкновения отдельных молекул газа. При этом коэффициент теплопроводности определяется соотношением:
=wlCv /3,
где w – средняя скорость перемещения молекул газа, l – средняя длина свободного пробега молекул при соударении, - плотность газа.
С увеличением давления в равной мере увеличивается плотность, уменьшается длина пробега и произведение l сохраняется постоянным. Поэтому коэффициент теплопроводности газов мало меняется с изменением давления. Исключения составляют очень малые (меньше 2,66*103 Па) и очень большие (2*109 Па) давления. Коэффициент теплопроводности газов лежит в пределах от 0,0006 до 0,6 Вт/(м*К). Поэтому воздух обладает свойствами хорошего теплоизолятора.
Коэффициент теплопроводности жидкостей описывается уравнением :
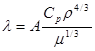 |
где Ср – теплоемкость жидкости при постоянном давлении, - плотность жидкости, - ее молекулярная масса. Коэффициент А пропорционален скорости распространения упругих волн в жидкости, не зависит от природы жидкости, но при этом А*Ср = const. Механизм распространения теплоты в капельных жидкостях можно представить как перенос энергии путем нестройных упругих колебаний. Коэффициет теплопроводности жидкостей лежит в пределах от 0,07 до 0,7 Вт/(м*К). Но жидкости, как правило, не используются в теплозащитной технике.
Коэффициент теплопроводности твердых тел . Определяется опытным путем или на основе эмпирических формул. В металлах основным передатчиком являются свободные электроны, которые можно уподобить идеальному одноатомному газу. Передача теплоты при помощи колебательных движений или в виде упругих звуковых волн не исключается, но ее доля незначительна по сравнению с переносом энергии электронным газом. При наличии разного рода примесей коэффициент теплопроводности металлов резко убывает. Это можно объяснить увеличением структурных неоднородностей, которое приводит к рассеиванию электронов. Так, например, для чистой меди =396 Вт/(м*К), для той же меди со следами мышьяка =142 Вт/(м*К). Как видно металлы не могут быть хорошими теплоизоляторами от обычной теплопроводности, хотя они хорошо справляются с отражением ИК- и других излучений в лучистом переносе энергии.
В диэлектриках с повышением температуры коэффициент теплопроводности увеличивается. Как правило, для материалов с большей плотностью коэффициент теплопроводности имеет более высокое значение.
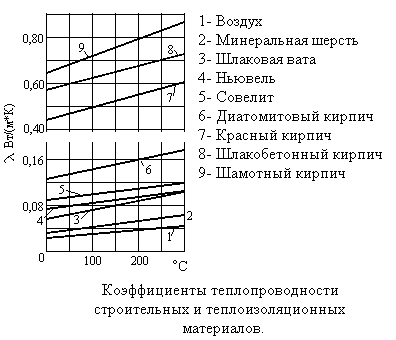
Теплопроводность зависит от структуры материала, его пористости и влажности. Зависимость теплопроводности материала от объемной влажности может быть выражена эмпирической формулой :
=с.м + w,
где с.м - коэффициент теплопроводности материала в воздушно-сухом состоянии; - приращение коэффициента теплопроводности на каждый процент увеличения объемной влажности; w – объемная влажность, %. Величину органических материалов при положительных температурах принимают равной 3.5*10-3 , а при отрицательных температурах 4*10-3 Вт/(м*К); неорганических материалов – соответственно 2,3*10-3 и 3,5*10-3 Вт/(м*К).
Теплоизоляционные материалы должны отвечать следующим нормам : они должны быть температуро- и морозостойкими, негорючими или обладать возможно меньшей горючестью, химически инертными. Они недолжны иметь запаха или воспринимать запахи, обладать достаточной механической прочностью, виброустойчивыми, должны легко обрабатываться и резаться, должны удовлетворять определенным экономическим показателям.
Материалов, обладающих в равной и полной степени всеми перечисленными свойствами, пока не существует. Из всех существующих теплоизоляторов можно выделить высокоэффективные материалы (с =0,045 Вт/(м*К) в сухом состоянии и с объемной массой до 100 кг/м3 ) :
1) Органические естественные материалы. К ним относятся различные породы растительных волосков или растительного пуха, находившие ранее применение, но теперь редко используемые.
2) Органические исскуственные материалы. Очень перспективными материалами этой подгруппы являются пенопласты, получаемые путем вспенивания синтетических смол. Пенопласты имеют мелкие замкнутые поры и этим отличаются от поропластов – тоже вспененных пластмасс, но имеющих соединяющиеся поры и поэтому не используемые в качестве теплоизоляционных материалов. В зависимости от рецептуры и характера технологического процесса изготовления пенопласты могут быть жесткими, полужесткими и эластичными с порами необходимого размера; изделиям могут быть приданы желаемые свойства (например, уменьшена горючесть).
Пенопласты делятся на термопластичные, или термообратимые, размягчающиеся при повторных нагреваниях, и термонепластичные (термонеобратимые), отвердевающие при первом цикле нагревания и не размягчающиеся при повторных нагреваниях; к первым относятся пенополистиролы (ПС) и пенополивинилхлориды (ПВХ), ко вторым – пенополиуретаны (ПУ), а также материалы на основе фенолоформальдегидных (ФФ), эпоксидных (Э), кремнийорганических (К) смол.
Коэффициент теплопроводности у пенопластов колеблется в пределах 0,03 – 0,045 Вт/(м*К).
3) Неорганические материалы. Представителем этой подгруппы является алюминиевая фольга (альфоль). Она применяется в виде гофрированных листов, уложенных с образованием воздушных прослоек. Достоинством этого материала является высокая отражательная способность, уменьшающая лучистый теплообмен, что особенно заметно при высоких температурах. Другими представителями подгруппы неорганических материалов являются исскуственные волокна : минеральная, шлаковая и стеклянная вата. Средняя толщина минеральной ваты 6-7 мкм, средний коэффициент теплопроводности =0,045 Вт/(м*К). Эти материалы не горючи, не проходимы для грызунов. Они имеют малую гигроскопичность (не более 2%), но большое водопоглощение (до 600%).
Таким образом, имеется большое количество теплоизоляционных материалов, из которых может осуществлятся выбор в зависимости от параметров и условий эксплуатации различных установок, нуждающихся в теплозащите.
Список литературы :
· А.И. Андрющенко «Основы технической термодинамики реальных процессов» М., «Высш. школа», 1975.
· И.В. Савельев «Курс общей физики» Издательство «Наука», М., 1973.
· «Теплопередача» В.П. Исаченко, В.А. Осипова, А.С. Сукомел. Москва Энергоиздат, 1981.
· Р.П. Грушман «Что нужно знать теплоизолировщику». Ленинград Стройиздат, 1987.
· Большая сов. энциклопедия. Москва «сов. энцикл.», 1976.
· Справочник по производству теплоизоляционных и акустических материалов. Китайцев В.А., М., 1964.
· Холодильные установки. Е.С. Курылев, Н.А.Герасимов. Ленинград Машиностроение, 1980.
09.11.1998
29-04-2015, 03:08
