Не преувеличивая, трактат Максвелла [9] можно назвать «Библией электромагнетизма» и физическими основами математического анализа, однако даже в учебной литературе повсеместно встречаются физически бессмысленные математические выражения “div![]() ” и “rot
” и “rot![]() ”. Такое формальное использование математики создает путаницу понятий и попросту мешает действительно разобраться в физическом содержании соотношений электродинамики. Это усугубляется и абсолютной системой единиц СГС, когда безразмерные коэффициенты e0 = 1 и m0 = 1 делают векторы
”. Такое формальное использование математики создает путаницу понятий и попросту мешает действительно разобраться в физическом содержании соотношений электродинамики. Это усугубляется и абсолютной системой единиц СГС, когда безразмерные коэффициенты e0 = 1 и m0 = 1 делают векторы ![]() и
и ![]() ,
, ![]() и
и ![]() физически тождественными, где Эрстед и Гаусс равны в пустоте, а в средах различаются только численно.
физически тождественными, где Эрстед и Гаусс равны в пустоте, а в средах различаются только численно.
Итак, согласно Максвеллу, в электродинамике линейные (циркуляционные) векторы ![]() и
и ![]() имеют размерность линейной плотности физической величины, а потоковые векторы
имеют размерность линейной плотности физической величины, а потоковые векторы ![]() ,
, ![]() и
и ![]() – ее поверхностной плотности. В частности, размерность вектора магнитной индукции
– ее поверхностной плотности. В частности, размерность вектора магнитной индукции ![]() равна поверхностной плотности момента импульса на единицу заряда, в системе СИ - Тесла. Экспериментально это наглядно иллюстрируется эффектом Эйнштейна-де Гааза, где в материальной среде при ее однородном намагничивании возникает механический момент вращения, направленный коллинеарно полю, обусловленный упорядочением собственных магнитных моментов, соответственно, моментов импульса электронов в атомах вещества среды. Следовательно, поле вектора
равна поверхностной плотности момента импульса на единицу заряда, в системе СИ - Тесла. Экспериментально это наглядно иллюстрируется эффектом Эйнштейна-де Гааза, где в материальной среде при ее однородном намагничивании возникает механический момент вращения, направленный коллинеарно полю, обусловленный упорядочением собственных магнитных моментов, соответственно, моментов импульса электронов в атомах вещества среды. Следовательно, поле вектора ![]() - это поле момента импульса среды, порождающее ее вращение. Поэтому в соотношении (4а) размерностью вихревого поля магнитного векторного потенциала
- это поле момента импульса среды, порождающее ее вращение. Поэтому в соотношении (4а) размерностью вихревого поля магнитного векторного потенциала ![]() является линейная плотность момента импульса на единицу заряда.
является линейная плотность момента импульса на единицу заряда.
В итоге, согласно формулам (9), локальной характеристике микрочастицы - моменту импульса на единицу заряда сопоставляется его полевой эквивалент - магнитный векторный потенциал ![]() с размерностью линейной плотности момента импульса на единицу заряда. что дает вторую фундаментальную корпускулярно-полевую пару: для электрона -
с размерностью линейной плотности момента импульса на единицу заряда. что дает вторую фундаментальную корпускулярно-полевую пару: для электрона - ![]() с единицами измерения (Джоуль∙секунда)/Кулон
с единицами измерения (Джоуль∙секунда)/Кулон![]() (Джоуль∙секунда)/(Кулон∙метр).
(Джоуль∙секунда)/(Кулон∙метр).
Вернемся к соотношению (5) связи вектора ![]() с вектором
с вектором ![]() . Как теперь показано, размерность вихревого поля вектора электрической напряженности
. Как теперь показано, размерность вихревого поля вектора электрической напряженности ![]() однозначно равна линейной плотности момента силы на единицу заряда с единицей измерения в СИ (Ньютон∙метр)/(Кулон∙метр), что естественно нисколько не опровергает традиционную единицу измерения этой величины Вольт/метр, а лишь уточняет ее физический смысл. Таким образом, в действительности соотношение (5) является полевым аналогом основного уравнения динамики вращательного движения твердого тела, что логически соответствует рассмотренным выше корпускулярно-полевым представлениям.
однозначно равна линейной плотности момента силы на единицу заряда с единицей измерения в СИ (Ньютон∙метр)/(Кулон∙метр), что естественно нисколько не опровергает традиционную единицу измерения этой величины Вольт/метр, а лишь уточняет ее физический смысл. Таким образом, в действительности соотношение (5) является полевым аналогом основного уравнения динамики вращательного движения твердого тела, что логически соответствует рассмотренным выше корпускулярно-полевым представлениям.
Подводя предварительный итог, приходим к заключению, что установленная здесь принципиальная двойственность физических параметров электрического заряда говорит о реальном существовании фундаментального «корпускулярно-полевого дуализма» природы электричества, кстати, схожего по названию с «корпускулярно-волновым дуализмом» в квантовой механике. Формально и здесь и там имеем неразрывную взаимосвязь материи с ее пространственно-временным собственным полем. Однако их сущностные различия принципиальны: корпускулярно-полевой дуализм реализуется на микро- и макроуровнях строения Материи и основан на объективном единстве частицы материи и ее собственного первичного векторного поля в реальном пространстве физического вакуума, что в свою очередь неразрывно связано с реально наблюдаемым обычным традиционным электромагнитным полем, а в концепции корпускулярно-волнового дуализма микрочастица представляется скалярной волной вероятности в абсолютно пустом, абстрактном пространстве.
Говоря более конкретно, фундаментальность корпускулярно-полевого дуализма Материи обусловлена тем, что как две стороны одной медали локальные характеристики микрочастицы (совокупно, и макрообъекта) находятся в неразрывной связи с ее собственными полевыми параметрами. Электрическому заряду ![]() , кратному кванту электрического потока - заряду электрона |e-|, соответствует электрический векторный потенциал
, кратному кванту электрического потока - заряду электрона |e-|, соответствует электрический векторный потенциал ![]() , а удельному (на единицу заряда) моменту, кратному кванту магнитного потока
, а удельному (на единицу заряда) моменту, кратному кванту магнитного потока ![]() , отвечает магнитный векторный потенциал
, отвечает магнитный векторный потенциал ![]() , при этом ориентации векторов полей
, при этом ориентации векторов полей ![]() и
и ![]() взаимно ортогональны.
взаимно ортогональны.
Итак, мы видим, что векторные потенциалы – это полноправные физически значимые поля, и учет этого обстоятельства позволяет углубить и кардинально модернизировать концептуальные основы классической электродинамики, где, в частности, необходимо ожидать, что обсуждаемая здесь система уравнений Максвелла будет лишь рядовым частным следствием.
Покажем конкретно, какую же роль играют векторные потенциалы в электромагнитных процессах и явлениях? Очевидно, здесь четко прослеживается реальная возможность обратить проведенные выше рассуждения вспять, поскольку из обсуждаемой концепции «корпускулярно-полевого дуализма» физических характеристик микрочастицы необходимо следуют электродинамические уравнения современной теории электромагнитного поля на базе системы соотношений первичной взаимосвязи ЭМ поля с компонентами электрической ![]() и магнитной
и магнитной ![]() напряженности и ЭМ векторного потенциала с электрической
напряженности и ЭМ векторного потенциала с электрической ![]() и магнитной
и магнитной ![]() компонентами:
компонентами:
(а) ![]() , (б)
, (б) ![]() ,
,
(в) ![]() , (г)
, (г) ![]() , (10)
, (10)
(д) ![]() , (е)
, (е)  .
.
Объединение соотношений (4) – (7) в систему взаимосвязанных уравнений (10) представляется весьма конструктивным, поскольку в этом случае возникает система дифференциальных уравнений, описывающих значительно более сложное и необычное с точки зрения общепринятых воззрений вихревое векторное поле, состоящее из совокупности функционально связанных между собой четырех полевых компонент. Конкретно оно состоит из реально наблюдаемых в эксперименте полей векторов электрической ![]() и магнитной
и магнитной ![]() напряженностей - поля электромагнитного силового взаимодействия частиц Материи и ненаблюдаемых напрямую полей электрического
напряженностей - поля электромагнитного силового взаимодействия частиц Материи и ненаблюдаемых напрямую полей электрического ![]() и магнитного
и магнитного ![]() векторных потенциалов - собственного электромагнитного поля частиц Материи, полевого эквивалента их локальных характеристик: заряда и спина, которые также напрямую ненаблюдаемы, а лишь опосредовано изучением их полей взаимодействия. Такое четырехкомпонентное векторное поле физически логично назвать реальным электромагнитным полем.
векторных потенциалов - собственного электромагнитного поля частиц Материи, полевого эквивалента их локальных характеристик: заряда и спина, которые также напрямую ненаблюдаемы, а лишь опосредовано изучением их полей взаимодействия. Такое четырехкомпонентное векторное поле физически логично назвать реальным электромагнитным полем.
Объективность существования указанного четырехкомпонентного вихревого поля иллюстрируется нетривиальными следствиями из полученных выше соотношений, поскольку подстановки (10д) в (10в) и (10е) в (10a) приводят к системе новых электродинамических уравнений, структурно аналогичной системе традиционных уравнений Максвелла (1), но уже для поля ЭМ векторного потенциала с электрической ![]() и магнитной
и магнитной ![]() компонентами:
компонентами:
(a) ![]() , (б)
, (б) ![]() , (11)
, (11)
(в) 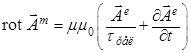 , (г)
, (г) ![]() .
.
Чисто вихревой характер компонент поля векторного потенциала обеспечивается условием калибровки - дивергентными уравнениями (11б) и (11г).
Соответственно, аналогичные математические операции с соотношениями (10) позволяют получить еще две других системы уравнений [8]:
для электрического поля с компонентами ![]() и
и ![]()
(a) 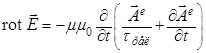 , (б)
, (б) ![]() , (12)
, (12)
(в) ![]() , (г)
, (г) ![]()
и для магнитного поля с компонентами ![]() и
и ![]() :
:
(a)  , (б)
, (б) ![]() , (13)
, (13)
(в) ![]() , (г)
, (г) ![]() .
.
Таким образом, уравнения системы (10) первичной взаимосвязи компонент ЭМ поля и поля ЭМ векторного потенциала, безусловно, фундаментальны. Кстати, если считать соотношения (10) исходными, то из них подобным образом [8] следуют и уравнения системы (1), справедливые для локально электронейтральных сред (![]() ). Существенно здесь и также то, что в системах (1), (11) - (13) их дивергентные уравнения представляют собой начальные условия в математической задаче Коши для соответствующих роторных уравнений, что делает эти системы уравнений замкнутыми.
). Существенно здесь и также то, что в системах (1), (11) - (13) их дивергентные уравнения представляют собой начальные условия в математической задаче Коши для соответствующих роторных уравнений, что делает эти системы уравнений замкнутыми.
Далее, как и должно быть, из всех этих систем электродинамических уравнений непосредственно следуют волновые уравнения для соответствующих полевых компонент (полностью аналогично выводу уравнения (2)) и соотношения баланса (аналогично выводу формулы (3)):
для потока момента ЭМ импульса из уравнений (11)
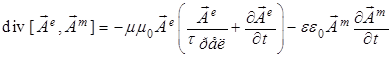 , (14)
, (14)
для потока электрической энергии из уравнений (12)
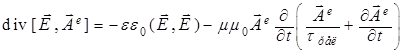 (15)
(15)
и для потока магнитной энергии из уравнений (13)
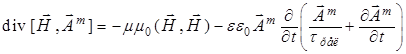 . (16)
. (16)
Эти соотношения еще раз подтверждают и аргументированно доказывают, что, наряду с ЭМ полем с парой векторных компонент ![]() и
и ![]() , в Природе существуют и другие поля: поле ЭМ векторного потенциала с компонентами
, в Природе существуют и другие поля: поле ЭМ векторного потенциала с компонентами ![]() и
и ![]() , электрическое поле с компонентами
, электрическое поле с компонентами ![]() и
и ![]() , магнитное поле с
, магнитное поле с ![]() и
и ![]() . Именно структура конкретного электродинамического поля из двух векторных взаимно ортогональных полевых компонент реализует способ его объективного существования, делает принципиально возможным его перемещение в пространстве в виде потока соответствующей физической величины. В реальности все эти потоки распространяются посредством лишь только одной как бы «обычной» плоской волны с взаимно ортогональными полевыми компонентами попарно коллинеарных векторов (
. Именно структура конкретного электродинамического поля из двух векторных взаимно ортогональных полевых компонент реализует способ его объективного существования, делает принципиально возможным его перемещение в пространстве в виде потока соответствующей физической величины. В реальности все эти потоки распространяются посредством лишь только одной как бы «обычной» плоской волны с взаимно ортогональными полевыми компонентами попарно коллинеарных векторов (![]() ,
, ![]() ) и (
) и (![]() ,
, ![]() ), совокупно переносящих в пространстве (см. соотношения баланса) электрическую (15) и магнитную (16) энергии, электромагнитные импульс (3) и его момент (14).
), совокупно переносящих в пространстве (см. соотношения баланса) электрическую (15) и магнитную (16) энергии, электромагнитные импульс (3) и его момент (14).
Такое четырехкомпонентное векторное поле следует называть реальным электромагнитным полем (или просто, электромагнитным полем), совокупно переносящего посредством традиционной электромагнитной волны электрическую и магнитную энергии, электромагнитные импульс и его момент, главной особенностью которого является фундаментальная неразрывная связь электромагнитных классических ![]() и
и ![]() полей взаимодействия с их векторными
полей взаимодействия с их векторными ![]() и
и ![]() потенциалами являющихся собственными первичными полями частиц микромира, обусловленными фундаментальным законом Природы - «корпускулярно-полевым дуализмом физических характеристик Материи».
потенциалами являющихся собственными первичными полями частиц микромира, обусловленными фундаментальным законом Природы - «корпускулярно-полевым дуализмом физических характеристик Материи».
Список литературы
1. Матвеев А.Н. Электродинамика. М.: Высшая школа, 1980.
2. Физический энциклопедический словарь. М.: СЭ, 1983.
3. Lebedew P.N. // Annalen der Physik. 1901. fasc. 4. Bd 6. S. 433-458.
4. Beth R.A. // Phys. Rev. 1935. V. 48. p. 471; 1936. V. 50. p. 115.
5. Вульфсон К.С. // УФН. 1987. Том 152. Вып. 4. С. 667-674.
6. Храпко Р.И. // Вестник РУДН. Сер. «Физика». 2002. № 10(1). С. 40-48.
7. Сидоренков В.В. // Труды VI Всероссийской конференции «Необратимые процессы в природе и технике». М.: МГТУ им. Н.Э. Баумана, 2011. Часть III. С. 215-219; // scipeople/users/8652252/ .
8. Сидоренков В.В. // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2006. № 1. С. 28-37; // Вестник Воронежского государственного технического университета. 2007. Т. 3. № 11. С. 75-82; // Материалы X Международной конференции «Физика в системе современного образования». Санкт-Петербург: РГПУ, 2009. Том 1. Секция 1. “Профессиональное физическое образование”. С. 114-117; // Необратимые процессы в природе и технике: Сборник научных трудов. Вып. 3. М.: МГТУ им. Н.Э. Баумана, 2010. С. 56-83.
9. Максвелл Дж. К. Трактат об электричестве и магнетизме. В 2-х томах. М.: Наука, 1989.
10. Антонов Л.И., Миронова Г.А., Лукашёва Е.В., Чистякова Н.И. Векторный магнитный потенциал в курсе общей физики / Препринт № 11. М.: Изд-во Физического факультета МГУ им. М.В. Ломоносова, 1998.
29-04-2015, 05:15
