3. КВАНТОВОМЕХАНИЧЕСКИЕ ПОТЕНЦИАЛЬНЫЕ ЯМЫ, ПОРОГИ И БАРЬЕРЫ ДЛЯ МИКРОЧАСТИЦ
В учебниках по квантовой механике обычно принято рассматривать примеры, описывающие поведение микрочастиц, находящихся в энергетических ямах или проходящих над (или под) энергетическими барьерами и порогами. При описании этих явлений, как правило, используются достаточно громоздкие математические формулы, из-за которых теряется физический смысл явлений.
Как пояснялось ранее, волновое уравнение Шредингера для стационарных состояний можно записать в форме (2.10) или в виде:
. (3.1)
Решением (3.1) в общем виде является функция:
. (3.2)
Для одномерной потенциальной ямы шириной а с бесконечно высокими (непроницаемыми) стенками, при использовании граничных условий 
и 
, получаем В = 0. Тогда уравнение (3.2) преобразуется в
, (3.3)
которое для А ≠ 0 формально выполняется при
, n = 0,1,2,3,… (3.4)
Последнее условие можно представить в виде
, n = 1,2,3,… (3.5)
где 
- длина волны де Бройля с чертой (
).
Выражение (3.5) имеет физический смысл – это отношение ширины потенциальной ямы к модам длин стоячих волн де Бройля, способных к существованию в этой потенциальной яме и характеризующих микрочастицу, находящуюся в яме. Это выражение показывает, что в потенциальной яме с бесконечно высокими стенками присутствуют (отбираются или резонируют) лишь моды волны, с длиной волны целочисленно дольной основной длине волны 
. Реально – половине этого значения.
Последнее выражение говорит о первоначальном квантовании в потенциальной яме длин волн или волновых векторов. Квантование уровней энергии для микрочастицы, находящейся в потенциальной яме, - это уже следствие отмеченного первоначального квантования дебройлевских длин волн.
Значит линейный или частотный спектр стоячих волн, описывающих состояние микрочастицы, находящейся в одномерной потенциальной яме с абсолютно непроницаемыми стенками, представляет собой основную длину волны (основную частоту) и бесконечно большой набор других волн, целочисленно дольных половине основной. Если же брать частоту волн де Бройля, то это основная частота и бесчисленное множество других частот, целочисленно кратных основной частоте.
Известное выражение, определяющее дискретный спектр уровней энергии микрочастицы, находящейся в одномерной потенциальной яме с бесконечно высокими стенками
, n = 1, 2, 3, … (3.6)
для понимания, лучше преобразовать и представлять в виде:
, n = 1, 2, 3, … (3.7)
Еще более понятным будет представление этого выражение в виде:
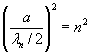, n = 1, 2, 3, … , (3.8)
откуда вытекает равенство
, n = 1, 2, 3, … , (3.9)
Последнее выражение показывает, что на ширине одномерной потенциальной ямы обязательно укладывается целое чисто дебройлевских полуволн (их гармоник), каждая из которых по частоте выше, а по длине волны меньше основной моды в целое число раз. В потенциальной яме с бесконечно высокими стенками число этих волн бесконечно большое множество. То есть, начиная с граничной частоты, имеется частотный спектр волн де Бройля. Этот спектр линейчатый и он расположен в сторону увеличения частоты до бесконечности.
Выше мы рассмотрели параметры микрочастицы, помещенной в одномерную потенциальную яму с непроницаемыми стенками. Теперь рассмотрим волновые и другие параметры для микрочастиц, находящихся в многомерных потенциальных ямах, а также в ямах, ограниченных по высоте.
Нормированная волновая функция, получаемая решением уравнения Шредингера для микрочастицы, находящейся в двумерной прямоугольной потенциальной яме с бесконечно высокими стенками, имеет вид:
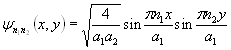, (3.10)
0 < x <a1, 0 < y < a2, n1, n2 = 1, 2, 3, …
Энергия микрочастицы описывается выражением
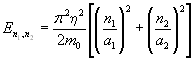, n1, n2 = 1, 2, 3, … (3.11)
Последнее выражение можно упростить и представить по аналогии с (3.8) в виде
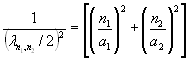, n1, n2 = 1, 2, 3, … (3.12)
Однако из последнего выражения нельзя получить простого соотношения, подобного (3.9). Выражение (3.12) говорит о том, что сложение волн происходит по правилу сложения векторных величин.
Аналогичное выражение для трехмерной потенциальной ямы имеет вид:
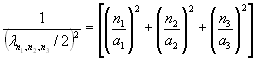, n1, n2, n3 = 1, 2, 3, … (3.13)
Таким образом, можно заключить, что частица, находящаяся в многомерной потенциальной яме с бесконечно высокими стенками, описывается набором стационарных волн, длины которых целочисленно дольны величинам сторон этой потенциальной ямы.
Уравнение Шредингера для частицы, находящейся в сферической потенциальной яме с непроницаемой стенкой радиуса а, имеет решение идентичное (3.3) – (3.5) [1]. Это означает, что в такой потенциальной яме стационарные волны де Бройля состоят из основной волны, половина длины которой равна длине окружности сферы, и бесконечно большого набора других волн, целочисленно дольных основной.
Волновое представление микрочастиц позволяет описывать их проникновение в стенки потенциальных ям и прохождение сквозь потенциальные барьеры конечной высоты. Свободное движение частицы в области, где уровень потенциальной энергии меньше уровня кинетической энергии, описывается уравнением (3.1). Его решение, записанное в показательной форме, имеет вид:
. (3.14)
В области потенциального порога или стенки потенциальной ямы, где потенциальная энергия превышает уровень кинетической энергии (U-E) > 0 волновое уравнение имеет другой вид:
. (3.15)
Решением этого уравнения является сумма двух экспонент с действительными показателями степеней
(3.16)
В результате сшивки двух функций (3.14) и (3.16) с учетом требований конечности и гладкости, предъявляемых к пси-функции, коэффициент А2 принимается равным нулю, коэффициент А1 принимается равным единице и определяются значения коэффициентов В1 и В2.
При прохождении микрочастицы над низким потенциальным порогом (E – U) >0 тоже наблюдается отражение. При этом уравнение Шредингера в любой зоне имеет вид (3.1), решения уравнения предстают в виде (3.14), а коэффициенты получают значения:
А1 = 1, В2 = 0, 
и 
. (3.17)
Квадрат коэффициента В1 представляет собой коэффициент отражения R частицы от высокого потенциального порога, а квадрат коэффициента А2, представляет собой коэффициент прозрачности D, причем D = 1 – R.
Думается, что коэффициент прозрачности прямоугольного потенциального барьера, обычно представляемый в виде
(3.18)
лучше записывать по иному, в виде:
. (3.19)
Такая форма представления не только понятнее, но и проще для запоминания. Выражение (3.19) говорит и о том, что высокочастотные составляющие волновой функции проходят потенциальные барьеры с большими потерями. То есть волновые свойства микрочастицы, попадающей внутрь потенциальной стенки или потенциального барьера, становятся качественно иными. По-видимому, имеет место также и качественно иное изменение микрочастиц, при преодолении ими потенциального порога и освобождении из связанного состояния, например для электронов, покидающих атом.
4. СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТЕЙ ГЕЙЗЕНБЕРГА, ИХ СИСТЕМНОЕ ПРЕДСТАВЛЕНИЕ И РАЗВИТИЕ
Известные соотношения неопределенностей, сформулированные Вернером Гейзенбергом,
(4.1)
и
(4.2)
не только безупречны с точки зрения их системного представления, но и вполне могут быть расширены на соотношения неопределенностей иных пар ФВ.
Системная иллюстрация приведенных соотношений показана на рис.1. Другие возможные закономерные соотношения неопределенностей иных пар ФВ показаны на рис.2. Все эти соотношения представляют собой системные соотношения ФВ, называемой действием актуальным, элементарным квантом которой является постоянная Планка или ее половина.
Ниже приведены не только показанные на рисунках, но и другие возможные системные соотношения неопределенностей, проистекающие из действия актуального. Соотношения приведены в наименованиях пар ФВ, участвующих в соотношении неопределенностей данного типа. Эти пары ФВ в микромире дополнительны друг другу и их невозможно одновременно точно измерить, вот они:
Энергия – Время;
Импульс – Длина;
Момент инерции – Угловая скорость;
Вязкость динамическая – Объем пространства;
Масса – Вязкость кинематическая;
Ток (расход) массы – Площадь;
Гравитационный потенциал – Изменение (вращение) объема;
Действие потенциальное – Градиент времени;
Сила – Кинематическая физическая величина с размерностью LT;
Динамическая физическая величина с размерностью МL – скорость.
Можно привести и иные соотношения данного типа, в том числе с участием электромагнитных величин.
При обсуждении этих новых соотношений обычно возникает возражение – какой смысл в квантовой механике имеет момент инерции или угловая скорость? На эти возражения можно дать такой ответ: эти соотношения следуют из системы и, вероятнее всего, каждое из этих соотношений имеет свой определенный смысл, но мы эти смыслы пока не улавливаем.
Надо отметить, что традиционное в квантовой механике определение возможных и невозможных для одновременного и точного измерения пар ФВ, что обычно выполняется при помощи определения коммутируемости их операторов, обладает несравненно большей сложностью и количественной ограниченностью.
5. СИСТЕМНЫЕ СООТНОШЕНИЯ ПОТЕНЦИАЛЬНОГО ДЕЙСТВИЯ И АНАЛИЗ СТРОЕНИЯ ВОДОРОДОПОДОБНЫХ АТОМОВ
В системе ФВ по рис.3 - рис.6 потенциальным действием названа величина, представляющая собой произведение силы на площадь или энергии на длину. В микромире, судя по всему, данная величина относится к сохраняющимся и квантуемым (вернее, дискретным). Рассмотрим этот вопрос подробнее.
На рис.3 представлены возможные системные соотношения ФВ действие потенциальное, выполненные аналогично рассмотренным выше соотношениям неопределенностей с участием действия актуального.
Проследим происхождение ФВ потенциальное действие и рассмотрим ее свойства на примере боровской теории строения водородоподобного атома (иона атома, имеющего Z протонов в ядре и один орбитальный электрон с зарядом – e).
Приведем уравнение, описывающее условие вращения в атоме электрона массой me по круговой орбите радиуса r под действием кулоновской силы со стороны ядра, а также формулу Бора для квантования момента импульса электрона [1]:
(5.1)
. (5.2)
Обычно совместным решением этих двух уравнений, определяют радиусы допустимых (стационарных) орбит электрона в водородоподобном атоме:
, n = 1, 2, 3… (5.3)
Здесь буквой а обозначен радиус первой стационарной орбиты в атоме водорода, так называемый боровский радиус.
Из выражений (5.1) и (5.2) можно определить не радиус орбит, а скорость электрона, находящегося на n - ой орбите:
. (5.4)
Если применить известное соотношение между ФФП: постоянной Планка, зарядом электрона и электрической постоянной
× 2a с , (5.5)
то выражение (5.4) становится совсем простым
(5.6)
Учитывая, что последнее соотношение определяется только скоростью света – с, поскольку 2 и α (постоянная тонкой структуры) представляют собой числовые константы, то можно констатировать, что с изменением номера орбиты именно скорость электрона меняется упорядоченно и целочисленно кратно относительно некого значения, связанного со скоростью света. Поэтому истинно квантуемой величиной (в смысле первичности и упорядоченности квантования) для электрона, находящегося в составе атома, скорее всего, является его скорость.
Если при этом масса остается неизменной, то это означает квантование импульса. А если квантуется импульс, то это значит целочисленно дольно изменяются длины волн. Вернее целочисленно кратно изменяется количество дебройлевских полуволн, укладывающихся на данной орбите.
Отметим, что радиус электронной орбиты изменяется (в теории) более сложным образом - по квадратичной зависимости и, судя по всему, не может быть первоначально квантуемой величиной.
Обычно принято анализировать не скорости, а энергии электрона, находящегося на n – ой орбите атома. Полная энергия электрона складывается из его кинетической энергии
(5.7)
и потенциальной энергии кулоновского взаимодействия электрона с ядром
. (5.8)
Суммарная энергия электрона составляет:
. (5.9)
С использованием соотношения (5.5) последняя формула тоже упрощается, принимая более простой и понятный вид:
. (5.10)
Таким образом, заключаем, что энергия электрона, находящегося в составе атома на разных энергетических орбитах, почти полностью определяется зарядом ядра, порядковым номером орбиты (зависимость квадратична) и величиной внутренней энергии электрона.
Используя известное выражение для рационализированной постоянной Планка,
, (5.11)
выражение (5.10), без учета знака, можно преобразовать в следующее:
. (5.12)
Выражение (5.12) аналогично (1.4). Оно определяет дебройлевскую частоту обращения электрона, находящегося на орбите водородоподобного атома. Эта частота также как и энергия электрона, имеет квадратичную зависимость от n. Нетрудно заметить, что для электрона водородоподобного атома указанное соотношение (энергии и частоты) остается неизменным.
Действительно, при любых изменениях энергии и частоты электрона, находящегося на определенной орбите атома, их соотношение всегда остается неизменным, и это соотношение мы называем постоянной Планка. При переходах электрона с одной орбиты на другую указанное соотношение если и изменяется, то это изменение обязательно целочисленно кратно минимальной величине.
Поскольку дебройлевская частота электрона связана с его дебройлевской длиной волны, а последняя с импульсом, то постоянная Планка есть также и соотношение орбитального импульса электрона с его длиной волны. Соотношение, которое для определенного энергетического уровня тоже является неизменным, а с изменением номера орбиты изменяется целочисленно кратно.
Из вышеприведенных формул можно сделать и другие важные выводы:
- при ограничении максимальной орбитальной скорости электрона величиной скорости света, числовое значение Z (формулы 5.6 – 5.10) не может превышать величину 137 @ a –1. Таким образом, водородоподобный атом (с одним электроном) в основном состоянии (n = 1) не может иметь число протонов, превышающее это число. Значит, постоянная тонкой структуры a своим значением в определенной степени ограничивает количество химических элементов, потенциально возможных к существованию в природе (здесь надо отметить возможность поправки на релятивистский эффект изменения массы);
- произведение кинетической (потенциальной, а также полной) энергии электрона на радиус его орбиты есть величина постоянная для любой стационарной орбиты атома, имеющего определенное значение Z.
. (5.13)
Последнее выражение можно записать по иному:
. (5.14)
Как видим в соотношении (5.14) имеется соотношение (5.5), которое представляет собой элементарный квант так называемого потенциального действия (не исключено, что 4p входит в состав этого кванта). Отметим, что ФВ потенциальное действие по размерности равна произведению силы на площадь и эта величина, похоже, является константой, общей и единой для любой электронной орбиты водородоподобного атома.
Из выражения (5.13) следует также постоянство произведения квадрата орбитальной скорости электрона на его орбитальный радиус. Это означает, что в потенциальном действии имеется (сопряженной или дополнительной к массе) еще одна сохраняющаяся ФВ, имеющая размерность L3T–2. Это соотношение характеризует вихреподобное строение электронных оболочек атома (если в нем есть движение, а оно есть). Отсюда следует, что третий закон Кеплера как бы соблюдается и в микромире.
Если рассмотреть более сложные уравнения, описывающие поведение электрона в составе водородоподобного атома с привлечением оператора квадрата момента импульса, например, уравнение (5.20) в учебнике [1], то с учетом выше изложенного, такие уравнения тоже можно попытаться упростить.
Итак, стационарное уравнение Шредингера в сферической системе координат (без привлечения обозначения оператора квадрата импульса) запишется в виде:
, (5.15)
где:
(5.16)
представляет собой радиальную часть, а
(5.17)
угловую часть оператора Лапласа, представляемого в полном виде так:
. (5.18)
С учетом (5.5) и других известных соотношений, выражение (5.15) преобразуемо к виду:
. (5.19)
В последнем выражении, кроме оператора Лапласа, представленного в сферических координатах, присутствуют: дебройлевская длина волны - конкретного электрона, его комптоновская длина волны - 
и расстояние от центра атома – r. Пси-функция в этом выражении будет зависеть как от радиуса, так и от угловых координат. Все возможные решения этого уравнения, по всей видимости, определимы и без привлечения так называемого оператора квадрата импульса, а исходя из более ясных представлений о дебройлевской длине волны электрона и целочисленной укладке половинок волн (включая моды) на различных электронных орбитах атома.
Системные соотношения потенциального действия, которые представлены на рис.4, скорее всего, подобны ранее рассмотренным системным соотношениям действия актуального. Из этого следует дополнительность друг другу и невозможность одновременного измерения в микромире следующие пар ФВ:
Действие актуальное – Скорость;
Энергия – Длина;
Сила – Площадь;
Натяжение – Пространственный объем;
Импульс – Вязкость кинематическая;
Вязкость динамическая – Поток объема;
Момент инерции – Ускорение.
Смысл некоторых из приведенных соотношений можно попытаться объяснить:
- ограничение на скорость перемещения автоматически означает и ограничение на минимальную величину кванта действия актуального. То есть, скорость света и постоянная Планка – взаимообусловленные ФВ;
- чем больше энергия микрочастицы, тем более компактно ее размещение в атоме или тем меньше ее собственный размер, если частица находится в свободном состоянии;
- чем меньший пространственный объем наблюдается, тем большие внутренние натяжения в нем обнаруживаются.
6. ИЗОЭНЕРГЕТИЧЕСКИЕ И ОЗОИМПУЛЬСНЫЕ ПОВЕРХНОСТИ АТОМОВ И МОЛЕКУЛ
В разделе 2 отмечалось наличие в уравнениях квантовой механики соотношения, характеризующегося отношением квадрата рационализированной постоянной Планка к удвоенному значению массы электрона. По размерности это отношение равно произведению энергии на площадь. В системе ФВ этой величине, а также величине, равной произведению импульса на площадь соответствующие места находятся (см. рис.3
29-04-2015, 02:08