Попробуем разобраться, что могут означать эти величины и существуют ли они в действительности. Исследуем опять область микромира, поскольку в макромире такие величины, вроде бы, не встречаются.
В разделе 5 мы изучили ФВ микромира действие потенциальное, которая является сохраняющейся величиной для любой n – ой электронной орбиты водородоподобного атома. Определим на примере той же модели водородоподобного атома, что собой будет представлять ФВ, равная произведению энергии электрона, находящегося на n – ой орбите, на площадь сферы, имеющей радиус, равный радиусу этой электронной орбиты.
Необходимые расчетные формулы и результаты вычислений сведены в таблицу.
Значение n |
Энергия одного электрона
|
Площадь сферы S =
|
Произведение Е× S =
|
Сравнение с результатом
|
| 1 |  |
4 |
 |
2 |
| 2 | /4 |
64 |
4 |
8 |
| 3 | /9 |
324 |
9 |
18 |
| 4 | /16 |
1024 |
16 |
32 |
| 5 | /25 |
2500 |
25 |
50 |
=
(Е× S)n = 1Как видно из таблицы, ФВ, равная произведению энергии электрона на площадь сферы с радиусом, равным орбитальному радиусу электрона, имеет вполне ясный физический смысл. Эта величина определяет максимальное количество электронов, которые могут быть размещены на том или ином энергетическом уровне. Как известно это количество равно 2n2, где n – номер энергетического уровня электронной орбиты.
Однако от общепринятого представления об увеличении радиуса электронных орбит, соответствующих большим энергетическим уровням, скорее всего, надо отказаться. Из опытных данных известно, что размеры атомов не позволяют электронам находиться на столь отдаленных расстояниях от ядра.
На основе данных приводимой выше таблицы, можно сделать предположение, что константной величиной, единой для всех электронных энергетических уровней, является произведение энергии одного электрона на их максимальное число, соответствующее определенному энергетическому уровню. Таким образом, мы выходим на представление о существовании в каждом атоме одной или нескольких изоэнергетических поверхностей, которые следует отнести к наиболее сохраняющимся физическим величинам.
По всей видимости, эта новая не совсем привычная величина определяет те внешние пространственные поверхности атома или молекулы (не обязательно сферические по форме), на которых размещаются электроны всех или отдельных энергетических уровней. Тогда изоэнергетическая поверхность атома, если она одна (или, лучше сказать, едина) вероятнее всего должна выступать в роли константы, определяющей свои собственные соотношения неопределенностей, наподобие ранее рассмотренных. Часть системных соотношений, иллюстрирующих эту мысль, можно видеть на рис. 5.
Подобные поверхности в атомных структурах для электронов с минимальной энергией (при температуре, равной абсолютному нулю) предсказаны и рассматриваются в квантовой механике уже давно. Этот энергетический уровень назван уровнем Ферми, а сама поверхность - поверхностью Ферми.
Из экспериментов известно, что с увеличением количества электронов на внешней электронной оболочке происходит уменьшение ее площади (своеобразное сжатие), а с ростом порядковых номеров атомов наблюдается периодическое изменение их в размерах. При этом, судя по всему, произведение суммарной энергии электронов на площадь электронной оболочки, в определенных пределах, остается величиной сохраняющейся. Поэтому, вполне возможно, что изоэнергетическая поверхность является также и квантуемой величиной в обозначенном нами понимании.
Очень возможно, что так называемые электроны атома, с физической точки зрения, представляют собой своеобразные моды колебательных движений, существующие всего лишь на одной или нескольких (немногих) пузыреподобных изоэнергетических электронных оболочках атома. По-видимому, эти изоэнергетические электронные оболочки могут иметь многолепестковый вид или размещаться одна в другой - наподобие матрешек. Во всяком случае, компьютерные модели, основанные на решении уравнений Шредингера, дают примерно такие картины.
Аналогично изоэнергетическим поверхностным величинам в микромире вполне возможно существование и изоимпульсных поверхностных величин. По крайней мере, на возможность существования таких величин указывает система ФВ.
Теперь от представлений об изоэнергетических и изоимпульсных поверхностных величинах вернемся к более привычным ФВ, в том числе к волне де Бройля.
В квантовой механике используются представления об энергии Ферми, а также об импульсе, скорости и температуре Ферми. Однако совсем не употребляется термин “длина волны Ферми”. Хотя этот термин, по нашим представлениям, должен быть первичен среди других понятий. По сути, мы говорим о той же волне де Бройля.
Энергия Ферми при абсолютном нуле температуры определяется известным выражением:
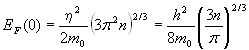. (6.1)
Привычным способом преобразуем это выражение с выявлением длины волны де Бройля, соответствующей этой энергии:
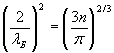
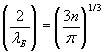
. (6.2)
Если энергия Ферми представляет собой максимальную энергию электронов, то соответствующая этой энергии длина волны де Бройля (которую можно называть длиной волны Ферми), представляет собой минимально возможную из всех волн, присущих данной совокупности электронов. Эта минимальная длина волны (вернее ее половина) полностью определяется лишь объемной плотностью электронов.
Этот факт весьма примечательный – оказывается, минимальная длина волны не зависит ни от массы, ни от скорости, ни от чего-либо иного, кроме пространственной плотности ансамбля микрочастиц.
Хорошо, а что мы можем сказать о максимальной длине волны де Бройля? Распределение Ферми-Дирака обозначает наличие меньших и совсем малых, даже нулевого значения, энергии электронов. Такие же меньшие значения, по сравнению с импульсом Ферми, будут значения других импульсов и волновых векторов.
Тогда, исходя из соотношения неопределенностей, можно говорить о возможности существования для электронной или иной совокупности микрочастиц, очень больших и даже бесконечно больших длин волн де Бройля. Применительно к электронному газу в проводниках это находит подтверждение практикой – когда маленькая антенна радиоприемника реагирует на длинные радиоволны километровой длины.
Однако с привычной точки зрения, как-то трудно воспринимается существование вокруг атомов или электронов стоячих волн больших размеров. Заметим, что для приема радиосигналов антенной используется не только пространственный (в полуволновом вибраторе), но и частотный (в LC – контуре) резонанс.
Обычно поверхность Ферми трактуется как граница, разделяющая электроны, находящиеся в вырожденном состоянии, и свободные электроны, приобретшие тепловую кинетическую энергию, превышающую уровень, называемый энергией Ферми.
Одновременно мы знаем, что свободными становятся внешние электроны атома, но более глубоко расположенные электроны атома, характеризуются еще большей кинетической энергией и, значит, еще меньшей длиной волны. Это означает, что привычное распределение Ферми-Дирака с энергией от нулевого значения до уровня Ферми соответствует лишь свободным электронам, не входящим в состав атомов. Это их скорости лежат в диапазоне от нулевой скорости до скорости Ферми. А электроны, входящие в состав атомов и подчиняющимися тому же распределению Ферми-Дирака, скорее всего, образуют свои внутриатомные изоэнергетические поверхности, расположенные внутри общей (для всех атомов) изоэнергетической поверхности Ферми.
Тогда поверхность Ферми, в традиционном ее понимании, это наименее энергоемкая (в удельном значении) поверхность, находящаяся внутри проводящего или полупроводящего материального образования. Другие изоэнергетические поверхности, располагаются внутри данной поверхности Ферми и они, в сравнении с ней, более энергоемки.
Может быть, свободные электроны, находящиеся внутри проводящих тел, следует воспринимать - как своеобразные колебания изоэнергетической поверхности Ферми. А связанные электроны, входящие в составе атомов и молекул, воспринимать в виде колебаний внутренних пузыреподобных изоэнергетических поверхностей. Указанные колебания не следует отождествлять с чисто механическими. Это могут быть особые параметрические колебания натяжения, плотности или иных параметров.
На рис.5 показаны некоторые очень интересные системные связи прогнозируемых в существовании изоэнергетических и изоимпульсных поверхностей с электромагнитными величинами. Эти системные связи способны помочь в уяснении физического смысла как новых, так и уже известных ФВ. Кроме того, вновь обнаруживаемые системные взаимосвязи ФВ представляют собой еще неизученные природные закономерности.
Общее примечание к дальнейшему изложению:
Далее необходимо обратить внимание обучающихся пользованию системой (и просто читателей) на то, что в системе по рис.5 (и рис.6) совершен отход от ранее применявшегося показа в ячейках с ФВ не размерности самих ФВ, а размерности системных элементов, имеющих строго упорядоченное расположение.
Конечно, строго упорядоченное расположение системных элементов удобно для общего восприятия, однако неоднозначность размерности этих элементов, зачастую вызывает смущение. Кто-то трудно идентифицирует привычные ФВ с непонятными системными элементами, а у кого-то, при взгляде на систему, просто возникает отторжение из-за необходимости вникать в что-то непривычное.
С целью возможного преодоления этих трудностей, система по рис.5 и рис.6 специально выполнена с использование различных систем размерности для системных элементов. Но в ячейках системы показывается не размерность элементов, а размерность ФВ в СИ. Сравнение этих двух вариантов и прошлых наших обозначений системных элементов позволяет лучше понять - как изменяются дополнительные размерностные коэффициенты в ячейках с ФВ, при изменении типа размерности системных элементов.
Например, сравнение LT- вариантов системы по рис.2-рис.4 и рис.6 (или MLT- вариантов по рис.1 и рис.5) позволяет понять достаточную условность и инвариантность представления дополнительных размерностных коэффициентов при ФВ. Во всех вариантах в системе действует правило выделенного параллелограмма, с помощью которого обнаруживаются системные (и закономерные) соотношения (между ФВ). Варианты по рис 1, рис.5 и рис.6 лучше тем, что дополнительные размерностные коэффициенты, стоящие при ФВ, помогают выявлению действительно закономерных взаимосвязей.
Следует отметить еще два преимущества представления системы по рис.5 и рис.6. Во-первых, данное представление системы постоянно иллюстрирует нам неуклюжесть и даже дикость размерностной системы СИ в части электромагнитных величин. Размерности полевых и структуро-средовые электромагнитные ФВ в системе СИ столь нелепы, что о выражении физической сущности этих ФВ их размерностью, не стоит даже и говорить.
Во вторых, данный вариант системы лучше подходит для электронного (компьютерного) представления. В электронном варианте легко решается вопрос показа многоуровневой системы ФВ. Кроме того, логика обнаружения системных (а значит и природных) закономерностей автоматически может заводиться в программу компьютера.
О возможности не только сознательного, но и автоматического поиска природных закономерностей, до появления подобной системы ФВ, можно было только мечтать.
7. О ФИЗИЧЕСКОЙ СУТИ ПОНЯТИЙ: ПОДВИЖНОСТЬ НОСИТЕЛЕЙ ТОКА И ПОСТОЯННАЯ ХОЛЛА
На рис.6 в системе физических величин показаны физические величины подвижность носителей тока и постоянная Холла, используемые при квантовом рассмотрении токовых явлений в физике твердого тела. Эти величины, с размерностной точки зрения, хотя и помещены на самостоятельные системные уровни, скорее всего, не являются самостоятельными ФВ. Подвижность - это величина, обратная индукции магнитного поля, а постоянная Холла – является величиной, обратной объемной плотности электрического заряда.
С физической сущностью постоянной Холла все вполне ясно. А вот уяснение обратно пропорциональной зависимости достаточно понятной величины подвижности носителей электрического тока и магнитной индукции не столь очевидно. Попробуем разобраться в этом.
Подвижность электрических зарядов (u0) в проводниках и полупроводниках определяется как отношение скорости перемещения носителей зарядов (электронов и дырок) к напряженности E0 электрического поля, вызывающего их движение.
. (7.1)
Движение электрических зарядов (величиной q) в стороннем магнитном поле с индукцией В сопровождается действием на них известной силы Лоренца:
, (7.2)
где α – угол между направлениями скорости v и индукции В.
Произведение vB sin α в этом выражении представляет собой поперечную (к основному направлению движения зарядов) составляющую напряженности электрического поля (
), обеспечивающую как раз действие на заряды поперечной силы Лоренца.
Отношение поперечной скорости перемещения электрических зарядов к указанной поперечной напряженности электрического поля () будет определять ту же подвижность электрических зарядов, поскольку подвижности как поперечная, так и продольная, вроде бы, должны быть одинаковы.
Известно, что чем больше скорость движения электрического заряда, тем больше величина индукции магнитного поля, возникающего при движении этого заряда. В нашем случае: чем больше индукция В, тем больше сила Лоренца и тем большей должна быть поперечная скорость перемещения электрических зарядов. В этом случае большее значение имеется и у поперечной составляющей электрического поля.
Поперечная составляющая электрического поля вызывает появление поперечной составляющей скорости в движении электрического заряда. Указанное движение заряда в поперечном направлении в том же магнитном поле с индукцией В вызовет (по правилу левой руки) появление как бы вторичной силы Лоренца, действующей уже прямо против основного движения заряда под действием первичного поля Е0. Таким образом, магнитное поле, внешне созданное или от собственного тока, обязательно тормозит направленное перемещение и, соответственно, ограничивает подвижность носителей электрического тока.
Не случайно, что внутри сверхпроводников, имеющих по определению бесконечно большую подвижность носителей тока, магнитного поле обязательно выталкивается вовне. Как магнитное поле связано с проводимостью обычных проводников и подвижностью носителей тока в этих проводниках - требуется еще изучать.
По всей видимости, до прояснения этого вопроса, физическую величину подвижность электрических зарядов целесообразно применять и использовать, несмотря на совершенно одинокое ее расположение в системе физических величин.
8. О ФИЗИЧНОСТИ ПРЕДСТАВЛЕНИЯ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ КВАНТОВЫХ СОСТОЯНИЙ
Устоявшиеся в квантовой механике представления о плотности распределения квантовых состояний в шестимерном фазовом пространстве с взаимно перпендикулярными осями x, y, z, px, py, pz, где полный объем состоит из произведения двух объемов - объема в пространстве координат и объема в пространстве импульсов, не очень-то понятны с физической точки зрения.
Попробуем внести ясность в эти представления на традиционном примере рассмотрения нерелятивистских электронов, находящихся в свободном состоянии.
Плотность квантовых состояний по энергии (без учета дискретности ее уровней), для единичного объема, обычно записывается в виде:
. (8.1)
В этом выражении dnE трактуется как число состояний, приходящееся в единичном объеме на интервал энергии от Е до Е + dE ([2] стр.178).
Полное число состояний, различных по энергии и находящихся в единичном объеме, равно:
. (8.2)
Последнее уравнение можно преобразовать к более простому и понятному виду:
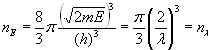. (8.3)
Выражение (8.3) показывает нам число полуволн де Бройля, содержащихся в единичном объеме. Это число, конечно же, равно числу дискретных уровней энергии или дискретных частот, содержащихся в единичном объеме. Только выражение для них будет не столь прозрачным и ясным для понимания. Прояснению ситуации несколько помогает только размерность, принимающая всегда одно и то же значение, обратное пространственному объему.
Число полуволн в единичном объеме, приходящихся на единичный интервал длины волны, определяется дифференцированием выражения (8.3)
. (8.4)
Знак минус здесь показывает увеличение плотности размещения волн с уменьшением их длины.
Формулы (8.3) и (8.4) достаточно просты для запоминания. Кроме того, с их помощью легко выводятся формулы, определяющие плотности состояний, приходящиеся на единичное значение того или иного параметра.
Для определения плотности распределений числа полуволн (частот, скоростей, импульсов и др.), приходящихся в единичном объеме на единичное значение соответствующей физической величины, требуется лишь знание взаимосвязи этих параметров с длиной волны и умение дифференцировать.
Таким путем легко выводятся следующие соотношения:
, (8.5)
, (8.6)
, (8.7)
. (8.8)
Количество отдельных уровней энергии, импульса и частот, приходящихся на единичный объем, совпадает с подобным количеством для длин волн. Это значение, выраженное через соответствующие параметры, имеет различный вид, но всегда идентично числу для длин полуволн.
, (8.9)
, (8.10)
, (8.11)
, (8.12)
В квантовой механике и статистической физике чаще всего рассматриваются энергетические распределения (8.5), объемная плотность которых, как известно, различна для классического газа и квантовых распределений из бозонов или фермионов.
Список литературы
1. Мартинсон Л.К., Смирнов Е.В. Квантовая физика: Учебное пособие. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004.
2. Савельев И.В. Курс общей физики: Учеб. пособие. В 3-х томах. Т. 3. Квантовая оптика. Атомная физика. Физика твердого тела Физика атомного ядра и элементарных частиц. – 3-е изд., испр. – М.: Наука, Гл. ред. физ.-мат. лит., 1987.
3. Чуев А.С. Физическая картина мира в размерности “длина-время”. Серия “Информатизация России на пороге XXI века”. – М.: СИНТЕГ, 1999 – 96 с. (Текст книги имеется на сайте автора: chuev.narod/).
4. Чуев А.С. О многоуровневой системе физических величин, выражающей законы природы, в частности, структуру и взаимосвязи электромагнитных величин. www.sciteclibrary/rus/catalog/pages/7335.html . 2004.
5. Чуев А.С. О целостном подходе в преподавании естественно-научных закономерностей с использованием системы физических величин//Материалы международной научно-практической конференции "Актуальные проблемы управления - 2004". 10-11 ноября 2004 г. Выпуск 4. Москва. ГУУ-2004.
6. Чуев А.С. Преподавание и изучение природных закономерностей с использованием системы физических величин (целостный подход).//Сборник тезисов докладов Третьей Всероссийской конференции “Необратимые процессы в природе и технике”, 24-26 января 2005 г. М: МГТУ им. Н.Э. Баумана, 2005.
29-04-2015, 02:08