Эмпирические законы, как показывает само их название, обнаруживаются на опытной, эмпирической стадии исследования. В этих целях наряду с наблюдением и экспериментом обращаются, конечно, и к теоретическим методам, таким, как индукция и вероятность, вместе с соответствующей математической техникой.
Теоретические законы никогда не могут быть открыты с помощью индуктивного обобщения частных фактов и даже существующих эмпирических законов. Причина этого состоит в том, что они имеют дело не с чувственно воспринимаемыми свойствами вещей и явлений, а с глубокими внутренними механизмами процессов. Здесь мы должны внести уточнение в прежнюю формулировку, где различие между теоретическими и эмпирическими законами сводилось к различию методов, используемых для открытия законов. Фактически, при более глубоком анализе оказывается, что само это различие имеет свои объективные основания в степени проникновения в сущность исследуемых процессов. Поэтому соотношение между теоретическими и эмпирическими законами можно рассматривать как выражение отношения между сущностью и явлением.
Теоретические законы проявляются через эмпирические, с их помощью они получают свое подтверждение и эмпирическое обоснование. В свою очередь эмпирические законы могут быть объяснены и поняты только на основе теоретических. Такое объяснение очень часто сводится к логической дедукции эмпирического закона из теоретического вместе с необходимой для этого дополнительной информацией. Все это дает нам основание утверждать, что теоретический закон по отношению к эмпирическому выступает как сущность к явлению. Такое же отношение существует и между эмпирическим законом и теми фактами, которые он систематизирует и объясняет.
Возникает вопрос: в какой связи находятся сущности, выражаемые с помощью эмпирического и теоретического законов? Характеристика закона как отражения “существенного в движении универсума” поможет нам разобраться в этой связи, а также в гносеологическом отличии эмпирических законов от теоретических.
По отношению к отдельным, конкретным, частным фактам и эмпирические и теоретические законы выступают как сущности явлений. Однако сущность, выражаемая в теоретическом законе, имеет более глубокий характер, ибо по отношению к частным фактам она представляет сущность второго порядка, в то время как эмпирические законы выступают для них сущностью первого порядка. “...Закон и сущность,- указывает В. И. Ленин,-понятия однородные (однопорядковые) или вернее, одностепенные, выражающие углубление познания человеком явлений, мира etc”. Поскольку теоретический закон по отношению к эмпирическому выступает, как сущность к явлению, то его открытие не может быть достигнуто на эмпирической стадии исследования. Какое бы количество эмпирической информации мы ни имели, в том числе и информации, сконденсированной в эмпирических законах, непосредственно с их помощью мы не можем открыть теоретический закон. Для этого необходим скачок от эмпирии к теории. Ученый строит догадки, делает предположения, выдвигает гипотезы и тщательно проверяет их на опыте, пока не придет к установлению закона.
Не существует никакого чисто логического пути от фактов к закону. И это вполне понятно, ибо “если бы форма проявления и сущность вещей непосредственно совпадали, то всякая наука была бы излишня...”. Но без эмпирической информации невозможно было бы проверить как эмпирические, так и теоретические законы. Связь эмпирических законов с фактами довольно ясна: по сути дела эти законы систематизируют и объясняют факты. Подобным же образом теоретические законы связывают в единое целое эмпирические законы и объясняют их. Такое объяснение принимает форму вывода эмпирических законов из теоретических. Конечно, непосредственно вывести эмпирический закон из теоретического невозможно, так как эмпирические понятия, или термины, не встречаются при формулировке теоретических законов, ибо последние имеют дело с ненаблюдаемыми, абстрактными объектами, свойствами и величинами. Эмпирические же законы выражают связи между наблюдаемыми, конкретными предметами, свойствами и величинами. По этой же причине теоретические понятия, или термины, в принципе не могут быть определены или сведены к эмпирическим. Вот почему оказались бесплодными усилия позитивистов Венского кружка перестроить всю науку с помощью редукции всех теоретических понятий и законов к эмпирическим терминам и законам.
В каком же смысле мы можем тогда говорить о выводе эмпирических законов из теоретических? Для такого вывода необходимо прежде всего установить связь между теоретическими и эмпирическими терминами. Поскольку теоретический термин нельзя определить с помощью эмпирического, то речь может идти только об установлении определенного соответствия между ними. Между тем в литературе по методологии и логике науки нередко можно встретить утверждения о возможности операционального определения теоретических понятий (П. Бриджмен) или установления “соотносительных определений” (Г. Рейхенбах). В действительности же ни о каком определении теоретических понятий с помощью эмпирических говорить здесь не приходится. Пожалуй, ближе всего связь между теоретическими и эмпирическими терминами может быть пояснена с помощью представлений о словаре и интерпретации. В самом деле, когда мы истолковываем среднекинетическую энергию молекул газа как его температуру, то по сути дела переводим или интерпретируем эмпирически ненаблюдаемый термин - кинетическую энергию молекул - посредством эмпирического термина - температуры. Температура тела может не только восприниматься на ощупь, но и точно измерена. А это имеет немаловажное значение для определения тех параметров, которые встречаются в уравнениях, связывающих между собой величины, относящиеся к ненаблюдаемым объектам. В противном случае мы не имели бы никакой возможности проверить теоретические законы.
Соотношение между теоретическими и эмпирическими законами во многом аналогично отношению между абстрактными геометрическими системами и интерпретированными, или конкретными, геометриями. Изучая геометрию Евклида в школе, мы обычно связываем с такими ее основными понятиями, как “точка”, “прямая” и “плоскость”, определенные пространственные представления. Так, точку можно представлять в виде крохотного пятнышка на бумаге, прямую линию - как путь светового луча в пустоте или же тонкую натянутую нить, плоскость - как идеально ровную поверхность. Все эти образы представляют лишь интерпретации основных понятий геометрии, но отнюдь не их определения. С равным успехом мы могли бы избрать в качестве таких интерпретаций объекты совершенно другого рода: например, точку определить с помощью трех действительных чисел, прямую - с помощью линейного уравнения и т. д. Важно, чтобы свойства рассматриваемых объектов удовлетворяли соответствующим аксиомам геометрии. Вот почему в абстрактной геометрии хотя и пользуются терминами “точка”, “прямая” и “плоскость”, но не связывают с ними каких-либо конкретных образов, а тем более не определяют основные геометрические понятия с помощью этих образов.
Аналогичное положение существует и в наиболее развитых отраслях естествознания. Здесь также теоретические термины связываются с эмпирическими, с той, однако, существенной разницей, что для интерпретации теоретических терминов мы должны располагать знанием о конкретном механизме связи между ненаблюдаемыми объектами теории. Действительно, для того чтобы установить соответствие между средней кинетической энергией молекул газа и его температурой, мы должны допустить существование мельчайших частиц газа - молекул и дополнительно к этому руководствоваться определенными гипотезами о характере движения этих частиц. Конечно, на первых порах теоретические модели оказываются весьма приближенными. Так, например, молекулы первоначально уподобляли биллиардным шарикам, а законы их столкновения сводили к механическим законам удара идеально упругих тел. Постепенно, по мере того, как обнаруживалось несоответствие между предсказаниями теории и результатами опыта, вносились уточнения и исправления в теоретические представления и таким образом достигалось лучшее описание и объяснение соответствующих явлений.
Развитие естествознания со всей убедительностью свидетельствует о том, что переход от многочисленных эмпирических обобщений и законов к сравнительно небольшому числу фундаментальных теоретических законов и принципов содействует более углубленному и адекватному постижению сущности исследуемых явлений. Одновременно с этим происходит также концентрация информации об этих явлениях. Вместо многих десятков и даже сотен различных обобщений и эмпирических законов наука открывает несколько теоретических законов фундаментального характера, с помощью которых оказывается возможным объяснить не только сотни эмпирических законов, но и огромное количество самых разнообразных фактов, которые на первый взгляд кажутся совершенно не связанными друг с другом. Так, например, когда Ньютону с помощью законов движения и гравитации удалось связать воедино движение земных и небесных тел, то тем самым было покончено с прежними представлениями о делении мира на “земной” и “небесный”, подчиняющихся якобы совершенно различным законам.
Поиски фундаментальных теоретических законов характеризуют стремление к познанию взаимосвязи и единства материального мира. Самая главная трудность, с которой здесь встречаются ученые, состоит в том, чтобы найти такие общие принципы, из которых с помощью некоторых правил соответствия можно вывести логически эмпирически проверяемые законы. Этой цели в значительной мере были посвящены усилия А. Эйнштейна в последние десятилетия его жизни. Стремление установить связь между электромагнетизмом и гравитацией привело его к. идее создания единой теории поля. Однако до сих пор основным недостатком этой теории продолжает оставаться то, что с ее помощью не удалось вывести какие-либо эмпирически проверяемые законы. Такие же недостатки присущи попыткам создания единой теории материи, предпринятым В. Гейзенбергом в последние годы. Однако эти неудачи не обескураживают исследователей, ибо они сознают необычайную сложность самой проблемы.
4. Динамические и статистические законы
Если основой дихотомического деления законов на теоретические и эмпирические является их различное отношение к опыту, то другая важная их классификация основывается на характере тех предсказаний, которые вытекают из законов. В законах первого типа предсказания носят точно определенный, однозначный характер. Так, если задан закон движения тела и известны его положение и скорость в некоторый момент времени, то по этим данным можно точно определить положение и скорость тела в любой другой момент времени. Законы такого типа в нашей литературе называют динамическими . В зарубежной литературе их чаще всего именуют детерминистическими законами, хотя такое название, как мы увидим ниже, вызывает серьезные возражения.
В законах второго типа, которые получили название статистических, предсказания могут быть сделаны лишь вероятностным образом. В таких законах исследуемое свойство, признак или характеристика относятся не к каждому объекту или индивидууму, а ко всему классу, или популяции в целом. Так, когда говорят, что в данной партии продукции 90% изделий отвечает требованиям стандартов, то это вовсе не означает, что каждое изделие обладает 90% качеством. Само выражение в процентах показывает, что речь здесь идет лишь о некоторой части или пропорции из общего числа изделий, которые соответствуют стандарту. Об отдельном же изделии без дополнительного исследования мы не можем заранее сказать, является оно качественным или нет. Этот элементарный пример достаточно ясно иллюстрирует основную особенность всех статистических законов, предсказания которых относительно отдельных индивидуумов или случаев имеют неопределенный характер. Именно эта неопределенность и заставляет исследователя вводить вероятностные понятия и методы для определения и оценки исхода индивидуальных событий массового случайного типа.
Уже классическая концепция вероятности, нашедшая наиболее полное выражение в трудах П. С. Лапласа, дает возможность оценивать исходы простейших массовых событий случайного характера. В этой концепции вероятность интерпретируется как “отношение числа случаев благоприятствующих к числу всех возможных случаев”. При этом, конечно, предполагается, что различные случаи являются равновозможными. Однако такая интерпретация имеет довольно ограниченную область применения. Действительно, равновозможных событий, о которых говорится в вышеприведенном определении вероятности, может просто не быть. Азартные игры, которые исторически явились первой моделью для применения и разработки классической концепции вероятности, специально организованы таким образом, что их исходы являются одинаково возможными, или симметричными. Если, например, игральная кость изготовлена достаточно тщательно, то при ее бросании выпадение любого числа очков от 1 до 6 является одинаково возможным. Поскольку в данном примере имеется шесть равновозможных случаев, благоприятствующим же является какой-то один случай, то его вероятность будет равна 1/6. По такой же схеме подсчитывается вероятность событий, которые можно свести к равновозможным. Иногда это не удается сделать даже в сравнительно простых примерах. Так, если ту же игральную кость изготовить с дефектами, тогда выпадение каждой грани не будет равновозможным. Еще более противоречащими классической концепции являются примеры, взятые из физической, биологической и социальной статистики. Допустим, что вероятность того, что данное вещество из радиоактивного материала будет испускать a-частицу, равна 0,0374. Ясно, что этот результат никак нельзя представить по схеме равновозможных событий. Тогда нам пришлось бы допустить 10000 равновозможных исходов, из них только 374 считались бы благоприятствующими. В действительности же здесь имеются лишь две возможности: либо в следующую секунду вещество испустит частицу, либо нет. Чтобы преодолеть подобные трудности, защитники классической концепции широко использовали так называемый принцип недостаточного основания, или одинакового распределения незнания. Согласно этому принципу, два события считаются равновероятными, если у нас не имеется основания для предположения, что одно из них осуществится скорее, чем другое. Поскольку же в качестве основания зачастую здесь выступало состояние знаний познающего субъекта, то само понятие вероятности лишалось своего объективного значения.
Частотная, статистическая или, как ее иногда называют, эмпирическая концепция вероятности исходит не из наперед заданной, жесткой схемы равновозможных событий, а из действительной оценки частоты появления того или иного события при достаточно большом числе испытаний. В качестве исходного понятия здесь выступает относительная частота появления того или иного признака, характеристики, свойства, которые принято называть событиями в некотором множестве или пространстве событий. Поскольку относительная частота определяется с помощью некоторой эмпирической процедуры, то рассматриваемую вероятность иногда называют еще эмпирической. Это не означает, что само теоретическое понятие вероятности в ее статистической или частотной интерпретации можно определить непосредственно опытным путем. Как мы уже отмечали в предыдущей главе, никакого операционального определения для статистической вероятности дать нельзя, ибо помимо эмпирической процедуры при ее определении мы обращаемся к теоретическим допущениям. В самом деле, осуществив те или иные наблюдения или эксперименты, мы можем точно подсчитать, сколько раз интересующее нас событие встречается в общем числе всех испытаний. Это отношение и будет представлять относительную частоту данного события:
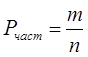 ,
,
где m означает число появлений данного события, а п - число всех испытаний. Хотя указанное отношение может принимать самые различные численные значения, тем не менее, как показывает практика, для весьма широкого класса случайных массовых событий оно колеблется вокруг некоторого постоянного значения, если число наблюдений или экспериментов будет достаточно велико. Таким образом, тенденция к устойчивости частот обширного класса массовых случайных явлений, обнаруженная на практике, представляет объективную закономерность этих явлений. Абстрактное понятие вероятности как меры возможности наступления события отображает прежде всего этот факт приблизительного равенства относительной частоты вероятности при достаточно большом числе испытаний. Такой подход к вероятности защищается большинством современных специалистов по статистике. Он нашел свое выражение и в широко известном курсе “Математические методы статистики” Г. Крамера. “Всякий раз, - пишет он, - когда мы говорим, что вероятность события Е в эксперименте x равна Р, точный смысл этого утверждения заключается просто в следующем: практически несомненно, что частота события Е в длинном ряду повторений экспериментаx будет приблизительно равной Р. Это утверждение будет называться также частотной интерпретацией вероятности”.
Частотный подход к вероятности дает возможность лучше понять специфические особенности статистических закономерностей. Поскольку любое вероятностное утверждение в статистической интерпретации относится не к отдельному событию, а к целому классу однородных или сходных событий, постольку и объяснения и предсказания, полученные с помощью статистических законов, не имеют такого строго однозначного характера, какой присущ динамическим законам. Чрезвычайно важно также отметить, что, в то время как в динамической закономерности необходимость выступает как бы в чистом виде, в статистической закономерности она прокладывает себе дорогу через массу случайностей. В совокупном действии многочисленных случайностей обнаруживается определенная закономерность, которая и отображается статистическим законом.
Как уже отмечалось, статистические закономерности с чисто формальной точки зрения отличаются от закономерностей динамического типа тем, что не определяют значение исследуемой величины достоверным образом, а указывают лишь ее вероятностное распределение. Динамический закон по своей математической форме может быть представлен функциональной связью типа:
У=Ф(x1 ,х2 ,...хn ).
Если заданы значения аргументов, то значение искомой функции определяется вполне однозначно. Статистические же законы характеризуют не поведение отдельных объектов, а скорее соотношения и зависимости, которые возникают вследствие совокупного действия целого ансамбля таких объектов. Поэтому они и выражают значения соответствующих величин вероятностным образом. Грубо говоря, статистика всегда дает нам какие-то средние величины, которые непосредственно нельзя приписать никакому индивидуальному объекту.
Вероятностный характер предсказаний статистических законов долгое время мешал тому, чтобы считать эти законы подлинно научными законами. Действительно, на первый взгляд может возникнуть впечатление, что статистические законы являются временным средством исследования, которое вводится лишь в целях удобства. И для такой точки зрения существуют даже некоторые основания. Так, например, многочисленные результаты, получаемые с помощью переписей, дают возможность в компактной и удобной форме обозреть огромную информацию, относящуюся к тысячам и миллионам людей. Однако в принципе эту информацию можно было бы выразить и в нестатистической форме. Статистика здесь вводится не потому, что иначе мы не можем описать индивидуумы, а именно в силу удобства.
Сложнее обстоит дело с объектами, изучаемыми физикой и химией. Описать поведение каждой молекулы чрезвычайно трудно, если не невозможно, но физики прошлого века считали, что такое описание в принципе возможно. Они полагали, что природа не ставит никаких границ ни для точности описания, ни для наблюдения
29-04-2015, 03:02
