Доминирующая роль законов в процессе научного объяснения наиболее сильно подчеркивается при так называемом эссенциалистском подходе, т. е. тогда, когда смысл объяснения сводится к раскрытию сущности реальных явлений и событий. B общем виде эта точка зрения не вызывает возражения, так как действительное объяснение достигается только тогда, когда раскрываются внутренние, существенные связи объясняемых явлений, событий или даже закономерностей. Вряд ли, однако, следует сводить объяснение к установлению логической связи “между отображением объясняемого объекта в языке и законом науки”. Сущность явлений, особенно сложных, может быть раскрыта зачастую лишь с помощью теории, представляющей не простую совокупность и даже не систему, состоящую из одних законов, а включающую в себя элементы и другого рода (исходные принципы, определения, гипотезы и различные утверждения теории). Подобно тому, как теоретический закон превосходит эмпирический по своей объясняющей силе, так и теория в целом дает более глубокое обоснование, чем любой отдельный закон или совокупность таких законов. Теория как наиболее развитая форма научного объяснения возникает, как правило, после открытия ряда отдельных законов той или иной области реального мира. Разумеется, верно, что законы составляют концептуальное ядро любой теоретической системы опытного знания. Но из этого вовсе не вытекает, что объяснение, опирающееся на теорию, всецело основывается на законах, а само противопоставление объяснения с помощью теории квалифицируется как иллюзорное.
По нашему мнению, в качестве общих посылок эксплананса любого научного объяснения или даже объяснения на уровне здравого смысла можно использовать обобщения самого различного характера. Наиболее совершенными считаются обычно объяснения, посылки которых содержат законы и теории науки универсального характера. Менее привлекательными выглядят объяснения, основанные на статистических законах. Гораздо менее надежными считаются объяснения, основанные на простых индуктивных обобщениях эмпирического опыта, к которым принадлежат объяснения, встречающиеся в повседневной жизни. Все перечисленные примеры представляют реальные объяснения, хотя и раскрывают сущность объясняемых явлений с различной степенью глубины и полноты.
8.1 Дедуктивная модель научного объяснения.
Объяснения, с которыми приходится встречаться, в науке, можно классифицировать по различным основаниям деления: характеру логической связи эксплананса с экспланандумом, составу и природе посылок, входящих в эксплананс, в частности по виду законов, которые фигурируют в посылках, и многим других признакам. Наиболее важной нам представляется классификация по способу логической связи эксплананса с экспланандумом, т.е. по тому способу, который используется для логического вывода объясняемого тезиса из объясняющих его посылок. Как мы уже отмечали, двумя основными формами логических умозаключений, применяемыми для объяснения, являются дедуктивные и индуктивные выводы. Соответственно этому мы и выделяем дедуктивную и индуктивную модели или схемы объяснения.
Дедуктивная модель научного объяснения является наиболее распространенной. Особенно широко ею пользуются в тех науках, законы которых могут быть выражены в точной математической форме (астрономия, механика, физика, физическая химия, молекулярная биология, математическая экономика и др.). Поскольку посылки дедуктивного вывода обеспечивают логически необходимый характер заключения, т.е. в нашем случае экспланандума, то естественно, что эта модель объяснения предпочитается индуктивной, где связь между посылками и заключением имеет не достоверный, а только вероятный характер. Важно при этом обратить внимание на то, что дедукция здесь понимается не в старом смысле традиционной логики, как умозаключение от общего к частному, а как любой вывод, заключение которого следует из имеющихся посылок с логической необходимостью, точно по принятым правилам дедукции.
Чтобы лучше понять дедуктивную модель объяснения, рассмотрим в качестве иллюстрации конкретный пример из действительной истории науки. Речь идет об объяснении “неправильностей”, или иррегулярностей, в движении планеты Уран. Эти иррегулярности нельзя было объяснить притяжением других, в то время известных планет Солнечной системы. Поэтому Леверье (и независимо от него Адаме) предположил, что они вызываются гравитационным воздействием новой, до сих пор неизвестной планеты. Последующие наблюдения блестяще подтвердили его гипотезу и тем самым предложенный им способ объяснения. Если логически реконструировать ход рассуждений Леверье, то их можно представить в виде следующей схемы. Во-первых, он исходил из ньютоновских универсальных законов движения и закона всемирного тяготения, которые в своей совокупности составляют большую посылку эксплананса. Во-вторых, в качестве меньшей посылки он использовал специфические характеристики планет Солнечной системы (их взаимные расстояния, массы, размеры и т.п.). Все эти посылки, вместе взятые, не смогли объяснить иррегулярности в движении Урана, Поэтому в качестве дополнительной меньшей посылки Леверье включил информацию о характере и величине наблюдаемых иррегулярностей в движении Урана. Опираясь на все перечисленные посылки, он смог вычислить период обращения, массу, орбиту и другие характеристики неизвестной, новой планеты, гравитационным воздействием которой и объяснил неправильности в движении Урана. Примечательно, что в этом примере объяснение органически связано с предсказанием.
Итак, мы видим, что в дедуктивной модели объяснение выступает как результат логического вывода объясняемого явления из объясняющих его посылок, причем главная роль в этих посылках принадлежит законам науки, универсальным утверждениям, в которых формулируются объективно необходимые, инвариантные отношения между предметами и явлениями реального мира. Большей частью при дедуктивном объяснении используются законы динамического типа или номические структуры вообще (т.е. общие высказывания, имеющие форму закона). Вот почему этот тип объяснения нередко характеризуют как дедуктивно-номологический. Такие объяснения обычно предпочитаются всем другим, так как их результат, или экспланандум, имеет достоверный, а не вероятный или проблематический характер.
Схематически дедуктивно-номологическая модель объяснения может быть представлена так:
Большая посылка:
эксплананс![]()
L1 , L2 ,...Lk-1 ,Lk
Меньшая посылка:
C1 ,C2 ,...Ck-1 ,Ck
![]()
экспланандумЕ
СимволамиL1 , L2 ,...Lk-1 ,Lk здесь обозначены универсальные законы динамического типа, или номические структуры вообще. C1 ,C2 ,...Ck-1 ,Cp представляют конкретные характеристики или условия, которые описывают некоторые специфические особенности рассматриваемых явлений. В математическом естествознании, в частности в математической физике, эти характеристики принято называть начальными условиями. Без них, вообще говоря, невозможен логический вывод утверждений, характеризующих отдельные, конкретные события, явления и предметы. Такого рода объяснения часто называют фактуальными, поскольку в этом случае цель объяснения сводится к объяснению некоторого факта. С логической точки зрения фактуальное объяснение сводится к дедукции экспланандума из соответствующего эксплананса, хотя объяснение в конечном итоге относится к некоторым реальным событиям, явлениям или предметам. В экспланандуме фактуального объяснения как раз и отображаются определенные свойства, аспекты или отношения индивидуальных предметов, событий и явлений. Правда, в некоторых случаях приходится встречаться и с известным обобщением или группировкой фактов, но все такие операции обычно не выходят за рамки эмпирического исследования.
Как мы уже отмечали, дедукция фактов или эмпирических высказываний единичного характера осуществляется с помощью законов простейшего типа, которые мы назвали эмпирическими. В повседневных рассуждениях вместо них обычно фигурируют элементарные индуктивные обобщения из нашего обыденного опыта. В случае гипотетических объяснений в роли законов выступают те или иные гипотезы.
Другой важной разновидностью дедуктивных объяснений являются объяснения, экспланандумом которых служат законы науки. В данном случае мы имеем дело с логическим выводом одних законов из других. Законы, которые встречаются в посылках эксплананса, должны обладать большей логической силой, чем закон, представленный в экспланандуме. Под термином “логическая сила” при этом понимается не что иное, как допустимость дедукции. Иными словами, если из одного утверждения или закона логически вытекает (дедуцируется) другое утверждение или закон, то первые из них считаются логически сильнее, чем вторые. Нередко также говорят, что чем логически сильнее закон, тем большей объясняющей силой он обладает.
Наиболее интересными случаями объяснения законов являются те, в которых менее глубокие и ограниченные законы объясняются с помощью более общих и глубокихзаконов, раскрывающих внутренний механизм протекания явлений. Типичным в этом смысле является соотношение между эмпирическими и теоретическими законами. В то время как первые выражают связи между эмпирически наблюдаемыми свойствами, величинами и отношениями реальных процессов и явлений, вторые характеризуют их более глубокие связи и структуру. Вследствие этого теоретические законы можно использовать для объяснения эмпирических законов: такое объяснение осуществляется с помощью логической дедукции эмпирических законов из теоретических. В данном случае в качестве экспланандума выступают эмпирические законы, а эксплананса-теоретические. Подобная дедукция оказывается возможной лишь тогда, когда теоретическим терминам дается соответствующая интерпретация и они связываются с эмпирическими с помощью некоторых правил соответствия. Эти правила наряду с теоретическими законами служат необходимой предпосылкой для вывода эмпирических законов, а следовательно, и для их объяснения.
Непосредственный вывод одних законов из других возможен лишь в том случае, когда и объясняющие и объясняемые законы относятся к одному типу или уровню познания. Так, например, располагая общим уравнением или законом газового состояния
PV=RT,
мы можем вывести из него эмпирически установленные Законы Бойля - Мариотта (P×V = const.) и Шарля - Гей-Люссака [vt = v0 (1 + at0 )]. В первом случае для этого достаточно принять температуру постоянной, а во втором - считать постоянным давление. По-видимому, в ряде случаев можно также говорить о дедукции менее общих теоретических законов из более общих.
Наконец, наиболее развитой формой дедуктивного объяснения является объяснение с помощью теории. В этом случае в качестве объясняющей посылки выступает не отдельный теоретический закон или некоторая их совокупность, а по крайней мере дедуктивное ядро теории: все ее исходные посылки и принципы, из которых в дальнейшем логически выводятся все другие положения теории, в том числе и те, которые имеют своей целью объяснение некоторых фактов и законов. Само собой разумеется, что при этом учитываются также определенные правила соответствия, которые связывают теорию с эмпирией.
8.2 Индуктивная модель объяснения
В последние десятилетия в логике и методологии все более широкое применение получает другая модель или схема научного объяснения, которая, правда, не обладает той убедительной силой и достоверностью, какая присуща дедуктивной модели. На этом основании ее иногда считают лишь временной попыткой объяснения, своего рода суррогатом, к которому приходится прибегать лишь в силу невозможности достижения более полного объяснения. Такой подход во многом определяется самим отношением к индукции, которая лежит в основе указанной модели объяснения. В самом деле, в то время как заключение дедуктивного вывода с логической необходимостью вытекает из посылок, заключение индукции, как правило, лишь в той или иной степени подтверждается этими посылками. Иными словами, если заключение дедукции имеет достоверный характер, то индукция обеспечивает лишь вероятные заключения. Вот почему сами индуктивные рассуждения иногда рассматривают лишь как эвристический способ мышления.
Необходимость обращения к индукции большей частью диктуется тем, что во многих объяснениях эмпирических наук приходится иметь дело со статистическими законами, выраженными в форме вероятностных утверждений. Как уже отмечалось, статистические законы в отличие от динамических характеризуют не индивидуальные события и явления, а только группы или классы однородных событий массового характера. Проще говоря, то, что утверждается в универсальном законе динамического типа, может быть перенесено на любой индивидуальный объект или событие. Статистические законы по своей природе не допускают такой возможности. Тем не менее, и такого рода законы можно использовать для объяснения и предсказания отдельных явлений и событий. В этих целях как раз и вводится теоретическое понятие вероятности, которое характеризует меру возможности осуществления события. Полнота объяснения и надежность предсказания в этом случае будут ниже, чем тогда, когда применяются универсальные законы динамического типа. Однако во многих важных ситуациях мы не располагаем подобными законами и поэтому должны обратиться к индуктивной схеме объяснения. Логический процесс, который мы используем для такого объяснения, очень часто определяют как индуктивную, или логическую вероятность. Он характеризует определенный типсвязи между посылками и заключением объяснения, т.е. экспланансом и экспланандумом. Эта вероятность по своему значению существенно отличается от вероятности статистической, с которой мы встречаемся при формулировке законов массовых случайных явлений в физике, биологии и социологии. Во избежание недоразумений следовало, быть может, просто называть логическую вероятность индукцией, но с этим термином также связаны нежелательные ассоциации. Дело в том, что в традиционной логике под индукцией обычно понимается процесс рассуждения, идущий от частного к общему. В современной же индуктивной логике этим термином обозначается всякое рассуждение или умозаключение, посылки которого в той или иной степени подтверждают заключение, т.е. по сути дела вероятностное высказывание. Важно также отметить, что формальная структура индуктивной вероятности хорошо описывается известными еще со времен Бернулли и Лапласа аксиомами исчисления вероятностей. Вот почему нам кажется целесообразным сохранить термин “логическая, или индуктивная, вероятность” при описании схемы индуктивного объяснения или предсказания.
Общая схема индуктивно-статистического объяснения может быть представлена в следующем виде:
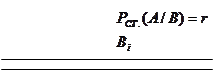 |
эксплананс (посылки делают
вероятным заключение)
экспланандум вероятно А
Большая посылка эксплананса такого объяснения представляет статистический закон, поэтому из него при фиксированных первоначальных условиях (меньшая посылка Вi ) может быть выведено лишь индуктивное заключение об отдельном событии или явлении А. Это заключение имеет также вероятностный характер, но сама вероятность здесь существенно отличается от статистической, ибо она выражает непосредственно не информацию о реальных событиях, а характер логической связи между посылками и заключением индуктивного объяснения. Поскольку заключение или экспланандум объяснения здесь логически не вытекает из посылок, а лишь в той или иной степени подтверждается ими, то в самой схеме мы отделяем эксплананс от экспланандума двойной чертой и дополнительно указываем на вероятностный характер заключения. Если величина этой вероятности, или степень подтверждения, является известной, то она может быть точно указана в самой символической записи. В этом случае экспланандум индуктивно-статистического объяснения можно записать в следующем виде:
Pинд. (А/Вi )=k.
Это выражение представляет символическую запись индуктивного заключения А при наличии некоторой совокупности условий В i . Таким образом, мы видим, что в индуктивно-статистическом объяснении используются две основные формы вероятности: статистическая и индуктивная (логическая). Если первая обеспечивает нас информацией о свойствах и закономерностях реального мира, то вторая устанавливает связь между экспланансом и экспланандумом объяснения.
При индуктивном объяснении с самого же начала возникает вопрос о том, какую степень подтверждения или логической вероятности следует признать достаточной для объяснения. Очевидно, если эта вероятность будет не больше половины, то такое объяснение вряд ли можно считать достаточно обоснованным. Равным образом мы не признаем надежным предсказание, вероятность которого не превосходит половины. Это обстоятельство существенно ограничивает класс индуктивных объяснений. Так, К. Гемпель относит к числу индуктивно-статистических объяснений только такие, степень вероятности которых приближается к 1. Иными словами, такого рода объяснения по существу приближаются к дедуктивным, так как их экспланандум вытекает из эксплананса почти с практической достоверностью (хотя теоретически практическая достоверность и отличается от достоверности дедуктивного заключения). В качестве конкретной иллюстрации Гемпель приводит пример с вытаскиванием шаров из урны, который достаточно ясно выражает его основную идею. Допустим, что мы наудачу вытаскиваем шар из урны, в которой находятся 999 белых и один черный шар. Если шары хорошо перемешаны, то вероятность извлечения белого Шара будет весьма велика (р = 0,999). Этот факт легко объяснить статистическими соображениями. Подобным же образом, по мнению Гемпеля, статистические законы, используемые при индуктивном объяснении, должны обладать такой высокой вероятностью, чтобы на их основе можно было делать надежные предсказания и объяснения. Некоторые авторы вообще отрицают правомерность индуктивного объяснения, утверждая, что в случае статистических обобщений и законов мы имеем дело не с объяснением, а с недостаточно надежными правилами недедуктивных умозаключений. Нетрудно заметить, что подобный подход к объяснению основывается на том, что единственно допустимой формой рассуждений в науке признается только дедукция, индуктивным же заключениям в лучшем случае отводится эвристическая роль. Вряд ли с таким подходом можно согласиться. Если индуктивно-статистические объяснения не признают за подлинные, полноценные объяснения, тогда следует также отказаться и от предсказаний, основанных на таких предпосылках. Но с этим не согласятся даже самые радикальные дедуктивисты.
И с теоретической и с практической точек зрения индуктивная модель объяснения играет существенную роль в науке. Часто она может значительно облегчить поиски более привычного дедуктивного объяснения, но во многих случаях сама проблема не допускает такого объяснения, и поэтому приходится обращаться к индукции и статистике.
В заключение остановимся на выяснении логической связи между дедуктивным и индуктивным объяснением. Поскольку индуктивный вывод допускает более ослабленные требования, чем дедуктивный, то целесообразно рассматривать индукцию как более общий тип рассуждения. Соответственно такому подходу мы будем выражать статистические законы в форме обобщенной, вероятностной импликации, впервые введенной Г. Рейхенбахом, а обычные универсальные законы динамического типа - в виде общей импликации математической логики.
В статистическом законе,
29-04-2015, 03:02
