![]()
![]()
![]()
![]()
![]()
![]()
![]() j(w)= - arctgTwФЧХ
j(w)= - arctgTwФЧХ
 |
0 w
![]() -45°
-45°
![]()
![]() -90°
-90°
2) Интегрирующее звено
Передаточная функция :

![]()
![]()
![]() W(w)АЧХ W(p)=
W(w)АЧХ W(p)=![]()
![]() ;ФЧХ :
;ФЧХ : ![]()
![]()
![]() 0 w
0 w![]()
![]()
3) Дифференцирующее звено
![]()
![]() C
C
![]()
![]()
![]()
![]()
![]()
![]()
![]() R
R
![]()
![]()
R L
![]()
![]()

![]() W(w) АЧХ Передаточная функция :
W(w) АЧХ Передаточная функция :
W(p)=Kp
АЧХ: W(w)=Kw
![]()
![]()
![]() ФЧХ: j(w)=
ФЧХ: j(w)=![]()
0 w
4) Форсирующее звено
![]()
![]()

![]() W(w) АЧХ
W(w) АЧХ
Передаточная функция:
![]()
![]()
![]()
K АЧХ : ![]()
![]()
![]()
![]() w ФЧХ :
w ФЧХ : ![]()
0
![]()
![]()
![]()
![]()


![]() j (w)
j (w)
![]()
![]()
![]()
![]()
![]()
0 w
5) Запаздывающее звено
АЧХ: ![]() =1 Передаточная функция :
=1 Передаточная функция :
ФЧХ: j(w)=wt![]()
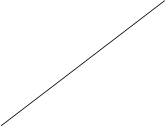
![]()
![]()
![]()
![]()
![]()
![]() j(w) ФЧХ
j(w) ФЧХ
АЧХ
![]()
![]()
![]()
![]()
![]() 1
1
Запаздывающее звено называется линией задержки, где
t=T - время запаздывания ЛЗ. j(w)=wT; ![]()
5) Колебательное звено
![]()
![]()
![]() Передаточная функция:
Передаточная функция:
![]()
![]()
![]()
![]()
![]()
![]()
![]() АЧХ
АЧХ ![]() - параметр затухания
- параметр затухания
![]() <1 - устойчивая система
<1 - устойчивая система
![]() >1 - самовозбуждающаяся
>1 - самовозбуждающаяся
система
ФЧХ
6) Неминимально фазовое звено
Передаточная функция:
АЧХ при a=b : ![]()
![]()
![]()
![]()
![]() ; W(w)=1
; W(w)=1
![]()
![]()
![]()
![]()
![]()
![]() ФЧХ при а=b :
ФЧХ при а=b : ![]() АЧХ
АЧХ
ФЧХ
Цифровые системы автоматического управления
Задан процесс: Будем рассматривать про-
![]()
![]()
![]() y(t) цесс y(t) в дискретные мо-
y(t) цесс y(t) в дискретные мо-
менты времени.
Такой процесс называется с
![]()
![]()
![]()
![]() дискретным временем
.
дискретным временем
.
![]()
![]()
![]()
![]() Значения этого процесса в
Значения этого процесса в
![]()
![]()
![]()
![]()
![]() дискретные моменты :
дискретные моменты :
![]()
![]()
![]() - значения
- значения
Существуют два типа процесса с дискретным временем :
1)Процесс с дискретным временем и непрерывным множеством
состояний. Это означает, что функция ![]() является непре-
является непре-
рывной ( если это случайный процесс, то ![]() непрерывна в
непрерывна в
среднем квадратическом).
ПЗС
![]()
![]()
![]() y(t) Преобразователь
y(t) Преобразователь ![]()
![]() - непрерывные функции
- непрерывные функции
ПЗС - прибор с зарядовой связью
![]() - интервал дискретизации во времени (квантование по
- интервал дискретизации во времени (квантование по
времени)
Для таких процессов составляются разностные уравнения :
![]() - 1-е приращение, конечная разность
- 1-е приращение, конечная разность
![]() - 2-я разность
- 2-я разность
2) Процесс с дискретным временем и дискретным множеством
состояний.
![]()
![]() y(t) АЦП
y(t) АЦП![]()
Процесс 2 отличается от процесса 1 тем, что ![]() записы-
записы-
вается в цифровом виде - дискретная функция, вся база
исследований другая. Квантование идет и во времени и
по уровню.
Очень часто делается бинарное квантование 0;1. В этом
случае аппаратура сильно упрощается.
Замечание :
1) В первом случае (ПЗС) если y(t)~![]() , то выход-
, то выход-
ной процесс ![]() , т.е. такой же, но дискрет-
, т.е. такой же, но дискрет-
ный.
2) ![]() - биномиальное распределение.
- биномиальное распределение.
Оказывается, если число уровней квантования ³ 8,то
их можно отождествить с непрерывными системами.
Представление дифференциальных уравнений, описывающих
системы автоматического управления конечных разностей
(1)
![]()
![]() - первая разность, аналог пер-
- первая разность, аналог пер-
вой производной
n - непрерывное время, непрерывное множество состо-
яний.
![]() - аналог 2й
- аналог 2й
производной
.......................................
![]() - аналог К-той производной
- аналог К-той производной
Если это подставить в непрерывное дифференциальное урав-
нение то получим следующее :
(2)
![]()
Если подставить в (2) разности, то получим :
(3)
![]() -
-
- разностное уравнение с дискрентным временем.
Z - преобразования
Аналогичны преобразованию Лапласа. Это очень удобный аппарат для исследования систем с дискретным временем в
частотной области. Для этого вместо экспоненты (для упро-
щения) вводится ![]() - это есть Z-преобразование. Для
- это есть Z-преобразование. Для
того, чтобы ввести Z-преобразование используется сле-
дующий прием связи непрерывного процесса X(t)и дискретно-
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() го
го ![]() (1)
(1)
![]()
![]() X(1),X(2) - выборка с дискрет-
X(1),X(2) - выборка с дискрет-
![]() нымвременем ¬
нымвременем ¬![]()
![]()
Рассмотрим преобразование Лапласа :
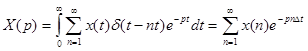 (2)
(2)
Формально введем новую переменную :
![]() (3)
(3)
Используя (2) и (3) получим
![]() (4)
(4)
(4) - называется Z-преобразования, показывает как перейти
от функции с дискретным временем (X(n)) к спектру
на Z-плоскости.(Оно проще преобразования Лапласа,
но имеет те же свойства и для разных дискретных
функций имеются специальные таблицы.
Устойчивость систем с дискретным временем
Системы с непрерывным временем характеризуются передаточ-
ной функцией (отношения 2х полиномов), тоже самое в Z-пре
образовании, только переменная не p = s± jw, a ![]() ,
,
![]() либо
либо ![]() (на линейной оси)
(на линейной оси)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
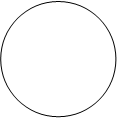
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() P-плоскость Z-плоскость
P-плоскость Z-плоскость
![]()
![]()
![]()
![]()
![]()
![]()
![]() (Система
(Система
устойчива)
![]() - окружность, следовательно левая комплексная полу-
- окружность, следовательно левая комплексная полу-
плоскость легче преобразуется во внутренность круга
Если полюсы передаточной функции находятся во внутреннос-
ти круга, то система устойчива, если полюсы находятся на
самом круге, то будет колебательный процесс, если вне
круга - система неустойчивая.
-устойчивая система - колебательная
![]()
![]()
 система
система
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() n
n
![]()
![]()
![]()
![]()
![]()
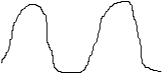
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
- неустойчивая система
n
Глава 3
Нелинейные динамические системы
Нелинейные динамические системы описываются дифференци-
альными уравнениями :
(1)
![]() , где
, где ![]() - вектор,
- вектор, ![]() ,
, ![]()
Если линейные дифференциальные уравнения имеют решения
(экспоненциальные), то для нелинейных дифференциальных
уравнений нет общих решений (за редким исключением), но
все реальные динамические системы нелинейны, некоторые
из них нельзя линеаризировать, как быть ?
Выход : 1) Там,где возможно, делается линеаризация правой
части уравнения (1).
Линеаризация - замена нелинейной функции на линейную.
(2) f(x,t)=A(t)x + B(t) + S(x,t)
S(x,t) - мало, им можно принебречь.
Если правая часть (1) не зависит от времени, то система
называется автономной
![]()
Линеаризация используется,как правило, для проверки
устойчивости системы. Для исследования свойств нелиней-
ных динамических систем, обычно используются качественные
и численные методы решения нелинейных дифференциальных уравнений. Теория нелинейных уравнений часто называется
теорией нелинейных колебаний.
Пример : Нелинейной динамической системы уравнений Вандер
Поля.
![]()
![]() - нелинейность.
- нелинейность.
![]() = const
= const
Дифференциальное уравнение называется нелинейным, если
оно нелинейно относительно разыскиваемой переменной (са-
мой переменной или ее производной) (нелинейность из-за
квадрата)
Требуется найти решение x(t) .
Существуют численные методы решения таких дифференциаль-
ных уравнений ( численные методы рассматриваются на сет-
ке с шагом ![]() ) . Решение получается не непрерывное , а
) . Решение получается не непрерывное , а
дискретное.
![]() Численные методы описыва-
Численные методы описыва-
![]()
![]()
![]()
![]()
![]() t ются в книге: Эльсгольц
t ются в книге: Эльсгольц
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ‘Теория дифференциальных
‘Теория дифференциальных
![]() уравнений и вариационное
уравнений и вариационное
исчисление’.
U
![]()
![]()
![]()
![]()
![]()
Численный метод Эйлера ( численный метод)
![]() ,
, ![]() ;
; ![]()
![]()
![]() (5)
(5)
Численный метод предназначен для решения не-
линейных дифференциальных уравнений.
Берется из апприорных (начальных условий)![]() ,
,
подставляется в правую часть уравнения (5) и
т.д. Это называется реккурентностью.
Качественная теория решения нелинейных диффе-
ренциальных уравнений (в приложении к нелинейным систе-
мам)
В отличие от численного метода (Метод Эйлера), который
дает решение в 1й точке ( не дает траекторию (нужно де-
лать 1000 точек, чтобы получить траекторию)).
Пуан Каре в 19 веке дал качественную теорию решения диф-
ференциальных уравнений, она используется для решения не-
линейных дифференциальных уравнений в виде некоторого фа-
зового портрета (некоторый графический материал, по ко-
торому можно анализировать траекторию движения динамичес-
кой системы, т.е. фактически получить решение (1-го из
решений).
На примере X и Y :
![]()
![]()
![]() y(1)
y(1)
![]() , где
, где ![]()
![]()
![]()
![]()
![]() f(x,y) - некоторая нели-
f(x,y) - некоторая нели-
![]()
![]()
![]()
![]()

 a dy нейная функция
a dy нейная функция
![]()
![]()
![]()
![]() - нелинейная
- нелинейная
функция
![]()
![]()
![]()
![]() x
x
Найти решение означает - найти y=j(x)(2) ,
которая удовлетворяет (1).
Пуан Каре развил метод , как найти (2) прямо на
плоскости.
Метод изоклин
Если f(x,y)=const, то ![]() , а
, а ![]() , на кривой
, на кривой
f(x,y)=const все производные имеют одно и тоже значение,
такая кривая называется изоклиной. (tga=const, a=const)
Можно вычислить множество изоклин, это множество дает по-
ле направлений. Касательная к этомуполю и есть решение,
т.о. это есть траектория, которую мы разыскиваем.
29-04-2015, 03:48
