Статистические методы раскрывают связи между изучаемыми явлениями. Однако необходимо твердо знать, что как бы ни была высока вероятность таких связей, они не дают права исследователю признать их причинно-следственными отношениями. Статистика, как о ней пишут известные английские ученые Д.Э. Юл и М.Дж. Кендэл (Теория статистики. М., 1960. С. 18—19.), «вынуждена принимать к анализу данные, подверженные влиянию множества причин». Статистика, например, утверждает, что существует значимая связь между двигательной скоростью и игрой в теннис. Но отсюда еще не вытекает, будто двигательная скорость и есть причина успешной игры. Нельзя, по крайней мере в некоторых случаях, исключить и того, что сама двигательная скорость явилась следствием успешной игры.
Чтобы подтвердить или отвергнуть существование причинно-следственных отношений, исследователю зачастую приходится продумывать целые серии экспериментов. Если они будут правильно построены и проведены, то статистика поможет извлечь из результатов этих экспериментов информацию, которая необходима исследователю, чтобы либо обосновать и подтвердить свою гипотезу, либо признать ее недоказанной.
Вот что нужно знать при использовании статистики.
Итак, были перечислены типы задач, с которыми чаще всего встречаются психологи. Теперь перейдем к изложению конкретных статистических методов, которые способствуют успешному решению перечисленных задач.
Первый тип задач. Статистические методы, примеры их применения для принятия решения.
Допустим, школьному психологу нужно представить краткую информацию о развитии психомоторных функций учащихся 6-х классов, в которых обучается 50 учеников. В процессе выполнения своей программы психолог провел диагностическое изучение двигательной скорости, применив методику, которая была описана выше (С. 240).
Для реализации своей программы психологу надлежало получить количественные характеристики, свидетельствующие о состоянии изучаемой функции — ее центральной тенденции, величины, показывающей размах- колебаний, в пределах которого находятся все данные отдельных учеников, и то, как распределяются эти данные.
Какими методами вести обработку — параметрическими или непараметрическими? Визуальное ознакомление с полученными данными показывает, что возможно применение параметрического метода, т.е. будут вычислены среднее арифметическое, выражающее центральную тенденцию, и среднее квадратическое отклонение, показывающее размах и особенности варьирования экспериментальных результатов.
Нельзя ограничиться вычислением только среднего арифметического, так как оно не дает полных сведений об изучаемой выборке. Вот пример. В одном купе вагона поместилась бабушка 60 лет с четырьмя внуками: 4 лет, двое по 5 и 6 лет. Среднее арифметическое возраста всех пассажиров этого купе 80/5 = 16.
В другом, купе расположилась компания молодежи: двое 15-летних, 16-летний и двое 17-летних. Средний возраст пассажиров этого купе также равен 16. Таким образом, по средним арифметическим пассажиры этих купе как бы и не различаются. Но если обратиться к особенностям варьирования, то сразу можно установить, что в одном купе возраст пассажиров варьирует в пределах 56 единиц, а во втором — в пределах 2.
Для вычисления среднего арифметического применяется формула:
![]()
а для среднего квадратического отклонения формула:
![]()
![]() В этих формулах х означает среднее арифметическое, х —
каждую величину изучаемого ряда, Z — сумму; s — среднее квадратическое отклонение; п —
число членов изучаемого ряда.
В этих формулах х означает среднее арифметическое, х —
каждую величину изучаемого ряда, Z — сумму; s — среднее квадратическое отклонение; п —
число членов изучаемого ряда.
Вернемся к опыту с проверкой двигательной скорости учащихся (С. 244).
В опытах участвовали 50 испытуемых. Каждый из них выполнил по 25 проб, по 1 минуте каждая. Вычислена средняя каждого испытуемого. Полученный ряд упорядочен и все индивидуальные результаты представлены в последовательности от меньшего к большему:
85— 93— 93— 99— 101—105—109—110—111—115—
115— 116— 116— 117— 117— 117— 118— 119— 121 —121 —
122 — 124 — 124 — 124 — 124 — 125 — 125 — 125 — 127 —127 —
127 — 127 — 127 — 128 — 130 — 131 — 132 — 132 — 133 — 134 —
134 — 135 — 138 — 138 — 140 — 143 — 144 — 146 — 150 — 158
Для дальнейшей обработки удобнее эти первичные данные соединить в группы, тогда отчетливее выступает присущее данному ряду распределение величин и их численностей. Отчасти упрощается и вычисление среднего арифметического и среднего квадратического отклонения. Этим искупается несущественное искажение/ информации, неизбежное при вычислениях на сгруппированные данных.
При выборе группового интервала следует принять во внимание такие соображения. Если ряд не очень велик, например содержит до 100 элементов, то и число групп не должно быть очень велико, например порядка 10—12. Желательно, чтобы при группировании начальная величина — при соблюдении последовательности от меньшей величины к большей — была меньше самой меньшей величины ряда, а самая большая — больше самой большой величины изучаемого ряда. Если ряд, как в данном случае, начинается с 85, группирование нужно начать с меньшей величины, а поскольку ряд завершается числом 158, то и группирование должно завершаться большей величиной. В ряду, который нами изучается, с учетом высказанных соображений можно выбрать групповой интервал в 9 единиц и произвести разбиение ряда на группы, начав с 83. Тогда последняя группа будет завершаться величиной, превышающей значение последней величины ряда (т.е. 158). Число групп будет равно 9 (табл. 1).
Вычисление среднего арифметического и среднего квадратическо-го отклонения.
Таблица 1
| Группы | Средние значения | Результат разноски | Итоги разноски | f•x | |||
| 83—91 | 87 |  / / |
1 | 87 | 36 | 1296 | 1296 |
| 92—100 | 96 | u | 3 | 288 | 27 | 729 | 2187 |
| 101—109 | 105 | LJ | 3 | 315 | 18 | 324 | 972 |
| 110—118 | 114 | 10 | 1140 | 9 | 81 | 810 | |
| 119—127 | 123 | 1300/ | 16 | 1968 | 0 | 0 | 0 |
| 128—136 | 132 | Ш | 9 | 1188 | 9 | 81 | 729 |
| 137—145 | 141 | Я | 5 | 705 | 18 | 324 | 1620 |
| 146—154 | 150 | L | 2 | 300 | 27 | 729 | 1458 |
| 155—163 | 159 | / | 1 | 159 | 36 | 1296 | 1296 |
n = 50 |
Σf • x = 6150 |
1-й столбец — группы, полученные после разбиения изучаемого ряда.
2-й столбец — средние значения каждой группы; этот столбец показывает, в каком диапазоне варьируют величины изучаемого ряда, т.е. х.
3-й столбец показывает результаты «ручной» разноски величин ряда или иксов: каждая величина занесена в соответствующую ее значению группу в виде черточки.
4-й столбец — это итог подсчета результатов разноски.
5-й столбец показывает, сколько раз встречалась каждая величина ряда — это произведение величин второго столбца на величины 4-го столбца по строчкам. Итоги 4-го и 5-го столбцов дают суммы, необходимые для вычисления среднего арифметического.
![]() 6-й столбец показывает разность среднего арифметического и значения x по каждой группе.
6-й столбец показывает разность среднего арифметического и значения x по каждой группе.
7-й столбец — квадрат этих разностей.
8-й столбец показывает, сколько раз встречался каждый квадрат разности; суммирование величин этого столбца дает итог, необходимый для вычисления среднего квадратического отклонения.
В заголовках 5-го и 8-го столбцов указывается, насколько часто встречается та или другая величина. Частота обозначается буквой f (от английского слова frequency).
Включение буквы f , означающей, насколько часто встречалась та или другая величина, ничего не изменяет в формулах среднего арифметического и среднего квадратического отклонения.
Поэтому формулы
![]()
![]()
вполне тождественны.
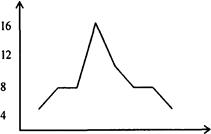
Рис.2
Остается показать, как вычисляются по формулам среднее арифметическое и среднее квадратическое отклонение. Обратимся к величинам, полученным в таблице:
![]() x = 6150 : 50 = 123. При составлении таблицы это число было заранее вычислено, без него нельзя было бы получить числовые значения 6, 7, 8-го столбцов таблицы.
x = 6150 : 50 = 123. При составлении таблицы это число было заранее вычислено, без него нельзя было бы получить числовые значения 6, 7, 8-го столбцов таблицы.
![]()
При обработке изучаемого ряда оказалось возможным применение параметрического метода, так как визуально в этом ряду распределение численностей приближается к нормальному. Это подтверждается и графиком (рис. 2, с. 251).
![]()
![]()
![]()
![]() Нормальное распределение обладает некоторыми весьма полезными для исследователя свойствами. Так, в границах x ± s находится примерно 68% всего ряда или всей выборки, в границах х
± 2s — примерно 95%, а в границах x ± 3s — 97,7% выборки. В практике исследований часто берут границы — x ±2/3s. В этих границах при нормальном распределении будут находиться 50% выборки; распределение это симметрично, поэтому 25% окажутся ниже, а 25% выше границ x ±2/3s. Все эти расчеты не требуют никакой дополнительной проверки при условии, что изучаемый ряд имеет нормальное распределение, а число элементов в нем велико, порядка нескольких сотен или тысяч. Для рядов, которые распределены нормально или имеют распределение, мало отличающееся от нормального, вычисляется коэффициент вариации по такой формуле:
Нормальное распределение обладает некоторыми весьма полезными для исследователя свойствами. Так, в границах x ± s находится примерно 68% всего ряда или всей выборки, в границах х
± 2s — примерно 95%, а в границах x ± 3s — 97,7% выборки. В практике исследований часто берут границы — x ±2/3s. В этих границах при нормальном распределении будут находиться 50% выборки; распределение это симметрично, поэтому 25% окажутся ниже, а 25% выше границ x ±2/3s. Все эти расчеты не требуют никакой дополнительной проверки при условии, что изучаемый ряд имеет нормальное распределение, а число элементов в нем велико, порядка нескольких сотен или тысяч. Для рядов, которые распределены нормально или имеют распределение, мало отличающееся от нормального, вычисляется коэффициент вариации по такой формуле:
![]()
В примере, который был рассмотрен выше,
V = (100-14,4)/123 = 11,7.
Выполнив все эти вычисления, психолог может представить информацию об изучении двигательной скорости с помощью примененной методики в 6-х классах. Согласно результатам изучения в 6-х классах получены: среднее арифметическое — 123; среднее квадратическое отклонение — 14,4; коэффициент вариативности — 11,7.
Непараметрические методы. Ранжирование, медиана, квартиль. Далеко не все материалы, получаемые в психологических исследованиях, подлежат обработке параметрическими методами. Если после ознакомления с изучаемым рядом исследователь убеждается в том, что этот ряд не имеет свойств нормального распределения, ему остается перейти на методы непараметрической статистики. С их помощью могут быть получены и центральная тенденция изучаемого ряда — медиана — и величина, позволяющая судить о диапазоне варьирования и о строении изучаемого ряда — квартильное отклонение.
Вот пример. После диагностических испытаний уровня умственного развития учеников 6-го класса полученные данные были упорядочены, т.е. расположены в последовательности от меньшей величины к большей. Испытания проходили 18 учащихся (табл. 2).
Таблица 2
| Учащиеся | Баллы | Ранги (R ) | Учащиеся | Баллы | Ранги (R ) |
| А | 25 | 1 | К | 68 | 10 |
| Б | 28 | 2 | Л | 69 | 11,5 |
| В | 39 | 4 | М | 69 | 11,5 |
| Г | 39 | 4 | Н | 70 | 14,5 |
| Д | 39 | 4 | О | 70 | 14,5 |
| Е | 45 | 6 | П | 70 | 14,5 |
| Ж | 50 | 7 | Р | 70 | 14,5 |
| 3 | 52 | 8,5 | С | 74 | 17,5 |
| И | 52 | 8,5 | Т | 74 | 17,5 |
Примечание. Буквами обозначены учащиеся, числами — полученные ими баллы по тесту.
Процедура ранжирования состоит в следующем. Все числа ряда в их последовательности получают по своим. порядковым местам присваиваемые им ранги. Если какие-нибудь числа повторяются, то всем повторяющимся числам присваивается один и тот же ранг — средний из общей суммы занятых ими ранговых мест. Так, числу 28 в изучаемом ряду присвоен ранг 2. Затем следуют трижды повторяющиеся числа 39. На них приходятся занятые ими ранговые места 3, 4, 5. Поэтому этим числам присваивается один и тот же средний ранг, в данном случае — 4. Поскольку места до 5-го включительно заняты, то следующее число получает ранг 6 и т.д.
При обработке ряда, не имеющего признаков нормального распределения — непараметрического ряда, — для величины, которая выражала бы его центральную тенденцию, более всего пригодна медиана, т.е. величина, расположенная в середине ряда. Ее определяют по срединному рангу по формуле Me = (п + 1)/2, где Me — означает медиану, п — как в ранее приводившихся формулах — число членов ряда. При нечетном числе членов ряда ранговая медиана — целое число, при нечетном число — с 0,5. Заметим, что числовое значение медианы может и не быть в составе самого обрабатываемого ряда.
Возьмем к примеру ряд в семь членов: 3—5—6—7—9—10—11.
Проранжировав его, имеем: 1—2—3—4—5—6—7.
Ранговая медиана в таком ряду равна: Me = (7 + 1)/2 = 4, этот ранг приходится на величину 7.
Возьмем ряд в восемь членов: 3—5—6—7—9—10—11—12.
Проранжировав его, имеем: 1—2—3—4—5—6—7—8.
Ранговая медиана в этом ряду равна: Me = (8 + 1)/2 = 4,5.
Этому рангу соответствует середина между двумя величинами, имеющими ранг 4 и ранг 5, т.е. между 7 и 9. Медиана этого ряда равна: Me = (7 + 9)/2 = 8.
Следует обратить внимание на то, что величины 8 в составе ряда нет, но таково значение медианы этого ряда.
Вернемся к изучаемому ряду. Он состоит из 18 членов. Его ранговая медиана равна: Me = (18 + 1)/2 = 9,5.
Она расположится между 9-й и 10-й величиной ряда. 9-я величина — 52, 10-я — 68. Медиана занимает срединное место между ними, следовательно, Me = (52 + 68)/2 = 60.
По обе стороны от этой величины находится по 50% величин ряда.
Характеристику распределения численностей в непараметрическом ряду можно получить из отношения его квартилей. Квартилью называется величина, отграничивающая 1/4 всех величин ряда. Квартиль первая — ее обозначение Q 1 — вычисляется по формуле:
![]()
Это полусумма первого и последнего рангов первой — левой от медианы половины ряда;
квартиль третья, обозначаемая Q 3 вычисляется по формуле:
![]()
т.е. как полусумма первого и последнего рангов второй, правой от медианы, половины ряда. Берутся порядковые значения рангов по их последовательности в ряду. В обрабатываемом ряду Q 1 = (1+9)/2 = 5, Q 3 = (10 + 18)/2 = 14.
Рангу 5 в этом ряду соответствует величина 39, а рангу 14 — 70. Следовательно, в данном ряду Q 1 = 39, а Q 3 = 70.
![]() Для характеристики распределения в непараметрическом ряду вычисляется среднее квартильное отклонение, обозначаемое Q
.
Формула для Q
такова: Q
= (Q
3
- Q
1
)/2. Для обрабатываемого ряда Q = (70 -
39)/2 = 15,5. Были рассмотрены статистическая обработка параметрического ряда (x и s), статистическая обработка непараметрического ряда (
M
е
и Q
). Параметрический ряд относится к шкале интервалов, непараметрический — к шкале порядка. Но встречаются также ряды, относящиеся к шкале наименований. Наиболее краткая характеристика такого ряда может быть получена с помощью моды, величины, которая выражает наивысшее числовое значение величин данного ряда, при п —
числе членов ряда. Следует заметить, что моду можно лишь условно считать выражением центральной тенденции в ряду, относящемуся к шкале наименований. Она выражает наиболее типичную величину ряда.
Для характеристики распределения в непараметрическом ряду вычисляется среднее квартильное отклонение, обозначаемое Q
.
Формула для Q
такова: Q
= (Q
3
- Q
1
)/2. Для обрабатываемого ряда Q = (70 -
39)/2 = 15,5. Были рассмотрены статистическая обработка параметрического ряда (x и s), статистическая обработка непараметрического ряда (
M
е
и Q
). Параметрический ряд относится к шкале интервалов, непараметрический — к шкале порядка. Но встречаются также ряды, относящиеся к шкале наименований. Наиболее краткая характеристика такого ряда может быть получена с помощью моды, величины, которая выражает наивысшее числовое значение величин данного ряда, при п —
числе членов ряда. Следует заметить, что моду можно лишь условно считать выражением центральной тенденции в ряду, относящемуся к шкале наименований. Она выражает наиболее типичную величину ряда.
Рассмотрим подробнее пример, приведенный выше (С. 242). Там речь шла об участниках некой конференции; в их числе были 3 англичанина, 2 датчанина, 5 немцев, 3 русских и 1 француз. Мода в данном ряду приходится на участников конференции — немцев. Число членов ряда равно — 13, а мода — Mo = 5.
Итак, мы рассмотрели статистические методы, применяющиеся для задач первого типа.
Второй тип задач. Психологу в его повседневной практической и исследовательской работе приходится искать ответы на различные вопросы. Предположим, что проведены диагностические испытания умственного развития у школьников шестых классов городской и сельской школ: можно ли в дальнейшем рассматривать обе школьные выборки как принадлежащие одной совокупности? По поводу неодинаковых условий обучения в городской и сельской школах высказано немало противоречивых суждений. Психолог в данном случае намерен опираться на экспериментальные факты. Чтобы прийти к какому-то решению, целесообразно проанализировать полученный экспериментальный материал. Это достаточно часто встречающаяся задача, встречаются и такие, где приходится решать тот же вопрос относительно нескольких, а не двух выборок. Это и есть задачи второго типа.
Перед психологом два ряда численностей. Прежде всего нужно установить, на какие статистические методы опираться — на параметрические или непараметрические? Применять параметрические методы следует в том случае, если оба ряда имеют распределение, не отличающееся от нормального. Если же один из рядов не соответствует этому требованию, то применение параметрических методов противопоказано.
Положим, оба ряда показывают распределение, допускающее применение параметрических методов. Сравнение величин центральных тенденций — в данном случае их представляют средние арифметические — не даст ответа на вопрос о том, относятся ли выборки к одной совокупности. Почти безошибочно можно утверждать, что средние арифметические не будут тождественными, но этого явно недостаточно для ответа на поставленный вопрос, ответ не был бы получен, даже если бы средние арифметические оказались равными. Для данного случая более всего подходит сравнение выборок по критерию t Стьюдента.
Перед тем как ознакомиться с техникой вычислений и интерпретаций результатов, получаемых при работе с критерием t Стьюдента, необходимо остановиться на некоторых статистических терминах; они постоянно встречаются в прикладной статистике.
В том разделе статистики, где заходит речь о проверке гипотез, постоянно приходится иметь дело с нуль-гипотезой, или нулевой гипотезой. При сравнении двух выборок нуль-гипотеза формулируется следующим образом: между изучаемыми выборками нет различия или, иначе, различие между ними несущественно. Все дальнейшие расчеты направлены на то, чтобы прийти к заключению верна ли нуль-гипотеза или от нее нужно отказаться, и в действительности существенная разница между выборками имеется. В других случаях в зависимости от содержания материала меняются формулировки, но вычисления показывают, какова вероятность нуль-гипотезы. Для обозначения нуль-гипотезы используется символ h 0 .
Допустим, что разница между выборками имеется. Исследователь встает перед вопросом, насколько существенна эта разница, как часто будет обнаруживаться она в последующем, когда придется работать с подобными же выборками. Самые общие соображения при этом таковы: если разница получена на небольшом материале (числе случаев, охваченных той или другой выборкой), то при повторном изучении таких же выборок разницу, возможно, найти и не удастся. Другое дело, если изучаемые выборки не малы. Далее важно, оказалась ли обнаруженная разница значительной. Это рассуждение и следует иметь в виду, когда в статистике речь идет об уровне значимости полученного коэффициента, параметра и пр. Уровни значимости представлены в специальных таблицах, которые обычно даются в учебниках статистики, есть такие таблицы и в конце этой главы. Какой уровень значимости можно признать удовлетворительным? В психологии и педагогике минимально допустимым для отказа от Н0
уровнем значимости признается
9-09-2015, 17:43
