А если не получен уровень значимости 0,95? Тогда нужно признать, что нуль-гипотезу не следует отвергать. Впрочем, иногда, по задачам исследования признается достаточным и более низкий уровень. В некоторых исследованиях цель состоит в том, чтобы прийти к утверждению нуль-гипотезы.
Обращаясь к таблицам уровней значимости, исследователь обнаруживает во многих из них специальный столбец с указанием степеней свободы, относящихся к полученному параметру или коэффициенту. Уровень значимости прямо зависит от того, каким числом степеней свободы обладает данный коэффициент или параметр. Число независимых величин, участвующих в образовании того или другого параметра, называется числом степеней свободы этого параметра. Оно равно общему числу величин, по которым вычисляется параметр, минус число условий, связывающих эти величины (Урбах В.Ю. Указ. соч. С. 161). Число степеней свободы и способы его определения всегда даются в окончательных формулах, которыми пользуется исследователь при статистической обработке своих материалов.
Рассмотрим пример с двумя выборками, которые, по мнению исследователя, можно рассматривать как подлежащие обработке параметрическим методом.
Двум группам шестиклассников по 6 человек было дано задание бросать мяч в корзину. Группы обучались по разным программам. Можно ли считать, что разница в программах сказалась на конечной результативности школьников? Для сравнения было взято число попаданий в корзину. Всего было дано по 10 проб.
Формула вычисления t :
где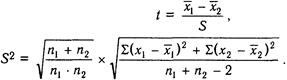
Материал, подлежащий обработке:
первая выборка, п = 6
| Исп. | х | ||
| А | 2 | -1 | 1 |
| Б | 4 | 1 | 1 |
| В | 6 | 3 | 9 |
| Г | 4 | 1 | 1 |
| Д | 1 | -2 | 4 |
| Е | 1 | -2 | 4 |
![]()
вторая выборка, п = 6
| Исп. | х | ||
| Ж | 5 | — | — |
| 3 | 4 | -1 | 1 |
| И | 2 | -3 | 9 |
| К | 8 | 3 | 9 |
| Л | 6 | 1 | 1 |
| М | 5 | — | — |
![]()
Ход вычислений показывает:

![]()
fd (число степеней свободы) =n1 -n2 -2=6+6-2= 10. По таблице уровней значимости t Стьюдента находим t 0,95 = 2,223. Существенность различия не доказана, хотя полученное значение t = 1,9 очень близко к требуемому уровню. Принимается Но . Нельзя утверждать, что выборки существенно различаются.
Для вычисления t существует несколько формул, различающихся только техникой расчетов.
Сравниваемые выборки могут быть неодинаковыми по объему. Применять параметрические методы можно лишь к материалу, обладающему определенными свойствами, о которых говорилось ранее. В других случаях следует обращаться к непараметрическим методам.
Ниже будет рассмотрена техника применения критерия Манна— Уитни, непараметрического метода, часто используемого в психологических исследованиях.
Предположим, что психологу нужно решить такую задачу. Есть ли различия между выборками школьников одного и того же класса, если одна выборка включает школьников, которые после контрольной работы проходили дополнительное обучение по коррекционным программам, другая — школьников, такого обучения не проходивших? Обе выборки малы, поэтому для проверки гипотез о существовании различий между выборками следует взять мощный критерий. Мощность критерия — это вероятность принятия при его применении правильного решения для отклонения ho ; чем выше эта вероятность, тем больше мощность критерия. Мощность любого критерия увеличивается вместе с увеличением объема сравниваемых выборок, а также со снижением того уровня значимости, на который ориентируется исследователь. Другими словами, если выборки велики, то принятие правильного решения относительно ho увеличивается. Ориентация на высокий уровень значимости, например 0,990 или 0,999, предполагает применение достаточно мощного критерия. В рассматриваемом примере выборки малы, а при установлении существенной разницы между ними, т.е. при отказе от ho желательно, чтобы уровень значимости был как можно выше, но не ниже 0,95.
Формула вычисления критерия Манна—Уитни такова:
или:
![]()
![]()
В примере сравнению подлежат результаты контрольной работы выборки A из 4 школьников, проходивших обучение по коррекционным программам, и выборки Б, состоящей из 7 школьников, никакого коррекционного обучения не проходивших. Последовательность действий, предусматриваемых вычислением всех нужных для решения задачи величин, такова.
1. Выписать в любом порядке число успешно решенных заданий школьниками сначала выборки А, затем выборки Б.
2. Проранжировать число успешно решенных заданий, объединив обе выборки.
3. Найти сумму рангов выборок А и Б раздельно.
Эти три действия дадут все необходимые для вычисления критерия данные.

Для проверки расчетов вычисляется:
R A + R B = N /2(1 + N ); т.е. 37 + 29 = 11/2(1 + 11), т.е. 66 = 66.
Имея величины U 1 и U 2 , следует обратиться к таблице уровня значимости. На совмещение строки четвертой со столбцом седьмым находим 3/25. По условиям таблицы, U 1 должно быть меньше верхней, aU 2 — больше нижней величины. Полученные величины показывают, что h o отвергается. Можно утверждать, что между выборками имеется существенное различие: результаты свидетельствуют о преимуществе выборки A .
Попарное сравнение. В предыдущем материале исследователь имел дело с двумя выборками. В обработку они поступают как два ряда чисел; каждый ряд есть результат экспериментов, проведенных с данной выборкой. Однако часто приходится встречаться с материалом, в котором даны два числовых ряда, но оба они получены на одной выборке; сюда относятся исследования, когда эксперименты проводятся до и после какого-то специального воздействия. Цель такого исследования состоит в том, чтобы установить, есть ли достаточно существенные изменения и можно ли утверждать, что специальное воздействие имело существенное значение.
Например, психологу было предложено ответить на такой вопрос:
влияют ли занятия физкультурой на общее самочувствие занимающихся школьников? Исследование он построил так: школьников просили отмечать на линейной шкале свое самочувствие до занятий физкультурой и после них.
Статистической обработке подлежат попарные сравнения показания одного и того же испытуемого до и после воздействия:
| до воздействия | после него | разность рядов «до» и «после» | |
| х | х2 | ||
| 3,2 | 3,8 | +0,6 | 0,36 |
| 1,6 | 1,0 | -0,6 | 0,36 |
| 5,7 | 8,4 | +2,7 | 7,29 |
| 2,8 | 3,6 | +0,8 | 0,64 |
| 5,5 | 5,0 | -0,5 | 0,25 |
| 1,2 | 3,5 | +2,3 | 5,29 |
| 6,1 | 7,3 | +1,2 | 1,44 |
| 2,9 | 4,8 | +1,9 | 3,61 |
| åx = 8,4; | åx2 = 19,24 | ||
| (åx)2 = 70,56 | |||
Нуль-гипотеза формулируется так: сравнение рядов до и после воздействия не дает оснований утверждать, что по измеряемому признаку произошли существенные изменения.
Выборка, подвергнутая изучению, состояла из 8 человек. Начнем с параметрического метода. Будет применен критерий t Стьюдента, его формула для попарного сравнения такова:
![]()
Нужно вычислить все величины, входящие в эту формулу. Для получения S используется формула:
![]()
Извлекая корень из полученной величины, узнаем значение S. Остается произвести по формуле все вычисления.
Ниже приводятся ряды, полученные в эксперименте (числа заимствованы из кн.: Бейли Н. Статистические методы в биологии. М., 1964).
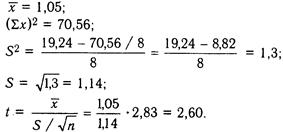
При вычислении t при попарном сравнении число степеней свободы равно п -1. По таблице уровней значимости для t находим, что для 7 степеней свободы t 0,95 должно быть не менее 2,36. Поскольку получена большая величина, следует признать, что налицо статистически значимое влияние занятий физкультурой на самочувствие школьников.
Из непараметрических методов для попарного сравнения удобен для пользования критерий Уилкоксона, правда, на небольших выборках этот критерий оказывается недостаточно мощным; его лучше применять на выборках объемом от 12 и более элементов.
Небольшие по объему выборки, однако, удобны для наглядного последовательного изложения техники расчетов.
Для использования этого критерия (его называют также знаково-ранговым) следует проранжировать, сначала не обращая внимания на знаки, весь перечень разностей между рядами «до» и «после». Если разность у отдельных испытуемых и в отдельных случаях нулевая, то она из ранжирования исключается и не входит в сумму рангов. В этом примере таких разностей (равных нулю) не встречается.
Далее нужно суммировать раздельно ранги разностей с положительным знаком и ранги разностей с отрицательным знаком. Значение критерия Т равно меньшей по абсолютной величине сумме рангов.
В этом примере Т = 3,5.
| Ряд разностей | +0,6 | -0,6 | +2,7 | +0,8 | -0,5 | +2,3 | +1,2 | +1,9 |
| Ранги | 2,5 | (2.5) | 8 | 4 | (1) | 7 | 5 | 6 |
Скобками указаны ранги разностей с отрицательными значениями. Но прежде чем отыскивать уровень значимости Т, нужно обратить внимание на то, что в данном случае критерий Уилкоксона — это двусторонний критерий. Как это понимать? Различают односторонние и двусторонние критерии. Отвергая нуль-гипотезу, выдвигают альтернативную ей гипотезу. При этом возникает вопрос: в какую сторону направлено отличие альтернативной гипотезы от H o — в положительную или отрицательную. Если исследование предполагает равно возможными и ту, и другую направленности, следует принять двусторонний критерий. Возможна вместе с тем такая постановка исследования, когда учитывается лишь одна направленность результатов. Так, сравнивая две выборки учащихся по освоении ими научных химических понятий, исследователь ставит ограниченную задачу — рассмотреть только возможность преобладания в этом освоении одной выборки над другой. В этом исследовании применим односторонний критерий.
При описании статистических методов всегда указывается, какого рода критерий подлежит применению — односторонний или двусторонний. В таблицах уровней значимости обычно значения для одностороннего и для двустороннего критериев даются либо в особых столбцах, либо в таблице указывается, какому значению одностороннего критерия соответствует значение двустороннего, и наоборот.
Возвращаясь к рассматриваемому примеру, следует признать, что для него при обработке с помощью критерия Уилкоксона применим двусторонний критерий: различия между показателями «до» и «после» в одних строках положительные, в других отрицательные, учитываются те и другие.
В таблице уровней значимости для критерия Т, имея в виду, что критерий двусторонний, находим, что для 0,95 уровня значение Т должно быть не более 3. Поскольку получено значение Т = 3,5, h o не следует отклонять.
Следовательно, критерий t Стьюдента свидетельствует о том, что H o подлежит отклонению, а T -критерий Уилкоксона свидетельствует о том, что нуль-гипотезу отвергать не следует. Такого рода расхождения, особенно при работе с небольшими выборками, вполне возможны. То, что критерий Уилкоксона Т всего на 0,5 превысил установленный уровень значимости, говорит о том, что при увеличении объема выборки в 1,5 или в 2 раза критерий Т также окажется значимым. В параграфе, где пойдет речь о планировании эксперимента, еще предстоит рассмотреть вопрос об объеме выборок.
Сравнение нескольких выборок по Уилкоксону. Иногда исследователю приходится сравнивать не две, а несколько выборок:
три, четыре и более. В таких случаях следует обратиться к простому и достаточно мощному непараметрическому критерию, представляющему собой модификацию критерия Уилкоксона. Метод позволяет сравнивать выборку с любой другой — вторую с третьей, первую с четвертой и т.д. Нужно, чтобы выборки были равными по численности.
Допустим, что учащимся 8-х классов четырех различных школ был предложен тест умственного развития. В школах использовались различные методы обучения и воспитания. Умственное развитие, как можно полагать, формировалось в каждой выборке в особых условиях. Эти условия и могли определить различия между выборками. Взято по 10 учеников из каждой школы. Их результаты и даны в таблице (табл. 3).
Таблица 3
| № | Школа I | Школа II | Школа III | Школа IV | ||||
| Результат | Ранг ( R 1 ) | Результат | Ранг (R 2 ) | Результат | Ранг (R 3 ) | Результат | Ранг (R 4 ) | |
| 1 | 96 | 36,5 | 96 | 36,5 | 32 | 9,5 | 40 | 15 |
| 2 | 82 | 30 | 100 | 39 | 27 | 3,5 | 38 | 14 |
| 3 | 80 | 28,5 | 93 | 34 | 68 | 23 | 42 | 18,5 |
| 4 | 78 | 25,5 | 87 | 33 | 78 | 25,5 | 32 | 9,5 |
| 5 | 34 | 11 | 100 | 39 | 54 | 21 | 31 | 8 |
| 6 | 42 | 18,5 | 28 | 5,5 | 56 | 22 | 28 | 5,5 |
| 7 | 42 | 18,5 | 80 | 28,5 | 83 | 31,5 | 42 | 18,5 |
| 8 | 69 | 24 | 94 | 35 | 22 | 1 | 30 | 7 |
| 9 | 79 | 27 | 25 | 2 | 41 | 16 | 36 | 13 |
| 10 | 100 | 39 | 83 | 31,5 | 27 | 3,5 | 35 | 12 |
| åR | 258 | 284,5 | 156,5 | 121 | ||||
Объединим результаты четырех школ в один ряд и проранжируем его. Для этого расположим ряд в порядке его возрастания и перенесем полученные ранги в таблицу (табл. 4).
Таблица 4
| Результат | Ранг | Результат | Ранг | Результат | Ранг | Результат | Ранг |
| 22 | 1 | 34 | 11 | 54 | 21 | 83 | 31,5 |
| 25 | 2 | 35 | 12 | 56 | 22 | 83 | 31,5 |
| 27 | 3,5 | 36 | 13 | 68 | 23 | 87 | 33 |
| 27 | 3,5 | 38 | 14 | 69 | 24 | 93 | 34 |
| 28 | 5,5 | 40 | 15 | 78 | 25,5 | 94 | 35 |
| 28 | 5,5 | 41 | 16 | 78 | 25,5 | 96 | 36,5 |
| 30 | 7 | 42 | 18,5 | 79 | 27 | 96 | 36,5 |
| 31 | 8 | 42 | 18,5 | 80 | 28,5 | 100 | 39 |
| 32 | 9,5 | 42 | 18,5 | 80 | 28,5 | 100 | 39 |
| 32 | 9,5 | 42 | 18,5 | 82 | 30 | 100 | 39 |
Подсчитаем сумму рангов по каждой школе.
åR = 258 + 284,5 + 156,5 + 121 = 820.
Проверочная формула: åR = N /2( N + 1) = 820, где N — общее число элементов, включающее все выборки. В этом примере оно равно 40.
Школа I åR = 258 |
Школа II åR = 284,5 |
Школа III åR = 156,5 |
Школа IV åR = 121 |
Шк. I åR = 258 |
26,5 | 101,5 | 137 |
Шк. II åR = 284,5 |
26,5 | 156,5 | 163,5 |
Шк. III åR = 156,5 |
101,5 | 156,5 | 35,5 |
Шк. IV åR = 121 |
137 | 163,5 | 35,5 |
Далее суммы рангов по выборкам размещаются в матрице.
На пересечении строк и столбцов указываются разности, показывающие, насколько отличается сумма рангов каждой выборки от других выборок.
По таблице значимости устанавливается, что при n = 10 (учитывается объем отдельной выборки) и при четырех условиях достигают уровня значимости 0,95 — величина 134 и более, а уровня значимости 0,99 — величина 163 и более. Следовательно, существенное статистически значимое различие имеется между 1-й и 4-й выборками и между 2-й и 4-й выборками; в последнем случае на уровне значимости 0,99.
Корреляции. В примере, рассмотренном выше (С. 260), сравнивались два ряда чисел, представляющие два ряда показателей одной и той же выборки; по смыслу задачи нужно было установить, существенная ли разница между этими рядами. Это были ряды, взятые из ситуации «до» и «после». Есть, однако, и многочисленные ситуации, когда исследователь заинтересован не в том, чтобы найти степень существенности разницы между вариационными рядами, а в том, чтобы найти, насколько тесно эти ряды связаны между собой, какова направленность этой связи. Так, группе школьников были предложены два теста, задания которых были построены на материале школьных дисциплин гуманитарного цикла — литературы и истории. Но в первом тесте для выполнения заданий требовалась актуализация умственного действия аналогии, а во втором — умственного действия классификации. Данные тестирования представлены в двух числовых рядах. Исследователю нужно ответить на вопрос, насколько тесно связаны эти два ряда. При строгой постановке эксперимента это исследование должно было пролить свет на то, какую роль играют умственные действия, указанные выше, на усвоение знаний в гуманитарном цикле.
Пример. Исследовалась выборка из 15 школьников. Для вычисления коэффициента корреляции, отражающего тесноту связи между двумя рядами, используются как параметрические, так и непараметрические методы.
До перехода к расчетам полезно рассмотреть любые коррелируемые ряды в их размещении в корреляционной решетке. По оси абсцисс размещаются показатели одного, а по оси ординат — другого ряда.
Теснота связи между рядами благодаря этой решетке становится легко обозримой. На рис. 3 схематически изображены различные виды соотношения коррелируемых рядов. Как видно, схемы отражают всего пять различных соотношений.

|
|
|
|
|
Рис. 3
На схемах можно усмотреть как тесноту связи, так и ее направленность. Схема 3 демонстрирует полное отсутствие связи между рядами; на схеме 5 показана нелинейная связь между рядами, та ее форма, которая показана на этой схеме лишь одна из возможных.
Коэффициент корреляции принимает значение от -1 (схема 4) до +1 (схема 1). В этих пределах возможны все числовые значения коэффициента корреляции. Если никакой связи между рядами не существует, то коэффициент равен 0 (схема 3). В подавляющем большинстве случаев коэффициент составляет величину, не достигающую 1. При положительной корреляции при увеличении числовых значений одного ряда соответственно увеличиваются числовые значения другого ряда. При отрицательной корреляции увеличению числовых значений одного ряда соответствует уменьшение числовых значений другого ряда.
Если исследователь убежден в том, что оба коррелируемых ряда можно рассматривать как ряды параметрические, то для вычисления коэффициента корреляции применяется параметрический метод по формуле Пирсона:
![]()
Существует много различных видов этой формулы, представляющих собой ее преобразования. Исследователь сам выбирает удобную для себя формулу. Об уровне значимости коэффициента корреляции судят по табл. 5, причем для г число степеней свободы fd = п - 2, где п — объем выборки.
Вычисление коэффициента корреляции по Пирсону. Коэффициент показывает тесноту связи между выполнением задач в тестах «Аналогии» и «Классификации». Данные по тесту «Аналогии» обозначены х, а по тесту «Классификации» — у.
Для упрощения расчетов введены некоторые тождества.
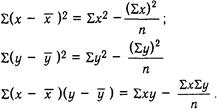
| Испытуемые | х | y | х2 | y2 | ху |
| А | 1 | 3 | 1 | 9 | 3 |
| Б | 2 | 4 | 4 | 16 | 8 |
| В | 3 | 5 | 9 | 25 | 15 |
| Г | 3 | 6 | 9 | 36 | 18 |
| Д | 4 | 6 | 16 | 36 | 24 |
| Е | 4 | 7 | 16 | 49 | 28 |
| Ж | 4 | 7 | 16 | 49 | 28 |
| 3 | 5 | 8 | 25 | 64 | 40 |
| И | 5 | 8 | 25 | 64 | 40 |
| К | 6 | 8 | 36 | 64 | 48 |
| Л | 6 | 8 | 36 | 64 | 48 |
| М | 7 | 9 | 49 | 81 | 63 |
| Н | 8 | 9 | 64 | 81 | 72 |
| О | 9 | 10 | 81 | 100 | 90 |
| П | 10 | 11 | 100 | 121 | 110 |
| n = 15 | 77 | 109 | 487 | 859 | 635 |
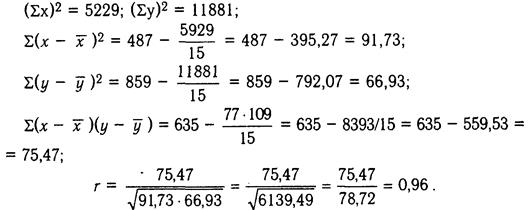
Число степеней свободы fd = п - 2 = 15 - 2 = 13. По таблице уровней значимости находим, что при 13 степенях свободы r 0,999 = = 0,760. Сравниваем это значение с полученным коэффициентом:
0,76 < 0,96.
Полученный коэффициент корреляции показывает, что между результатами в тестах «Аналогии» и «Классификации» имеется связь. Высокий уровень значимости свидетельствует о том, что эта связь с высокой вероятностью будет воспроизводиться в таких же экспериментах.
Вычисление коэффициента корреляции по Спирмену (коэффициент ранговой корреляции).
Исследовательское задание указано на с. 266. Формула ранговой корреляции такова:
![]()
где d — разность рангов ряда х и ряда у т.е. ( Rx - Ry ).
Таблица 6
| Испытуемые | х | Rx | y | Ry | dRx Ry | R2 dRxR y |
| А | 1 | 1 | 3 | 1 | 0 | 0 |
| Б | 2 | 2 | 4 | 2 | 0 | 0 |
| В | 3 | 3,5 | 5 | 3 | 0,5 | 0,25 |
| Г | 3 | 3,5 | 6 | 4,5 | 1 | 1 |
| Д | 4 | 6 | 6 | 4,5 | 1,5 | 2,25 |
| Е | 4 | 6 | 7 | 6,5 | 0,5 | 0,25 |
| Ж | 4 | 6 | 7 | 6,5 | 0,5 | 0,25 |
| 3 | 5 | 8,5 | 8 | 9,5 | 1 | 1 |
| И | 5 | 8,5 | 8 | 9,5 | 1 | 1 |
| К | 6 | 10,5 | 8 | 9,5 | 1 | 1 |
| Л | 6 | 10,5 | 8 | 9,5 | 1 | 1 |
| М | 7 | 12 | 9 | 12,5 | 0,5 | 0,25 |
| Н | 8 | 13 | 9 | 12,5 | 0,5 | 0,25 |
| О | 9 | 14 | 10 | 14 | 0 | 0 |
| П | 10 | 15 | 11 | 15 | 0 | 0 |
n = 15 n2 = 225 |
Σd2 RxRy = 8,5 | |||||
fd = п - 2 = 15 - 2 = 13.
Производится раздельное ранжирование ряда х и ряда у. Вычисляется разность рангов d попарно. Знак разности не существенен, так как по формуле нужно возвести d в квадрат. Далее действия определяются формулой:
![]()
По таблице уровней значимости r > r0,99 (0,98 > 0,70).
Коэффициенты, вычисленные двумя разными способами, как и нужно было ожидать, чрезвычайно близки друг к другу; отличаются они на 0,02, что никакого значения практически не имеет.
Нельзя трактовать коэффициент корреляции как величину, означающую процент взаимозависимых связей вариант двух коррелируемых рядов, т.е. например, коэффициент 0,50 трактовать как 50% таких связей этих рядов. Это далеко не так. Об этом проценте вообще
9-09-2015, 17:43
