Разложимые показатели расслоения

Кафедра: Социология и Обществознание

Реферат

на тему: Разложимые показатели расслоения

Москва, 2008 г.

1. Свойства расслоения

Показатели расслоения рассчитываются обычно для отдельных регионов страны, так как условия жизни и работы в отдаленных друг от друга районах могут быть и бывают для больших стран весьма разными. При расчете общего показателя расслоения для всей страны затруднительно и дорогостояще начинать все с самого начала, как это приходится делать, например, для коэффициента Джини. В последнем случае приходится либо согласовывать интервалы по доходам, что нежелательно из-за различных доходов и расходов в районах, либо передавать в центр или на следующую ступень иерархии данные о доходах домохозяйств, получая по ним новые доходные группы, т.е. забывать всю уже проделанную работу.

Если таких районов много, как субъектов федерации в России, то возникает вопрос, нельзя ли по уже рассчитанным местным коэффициентам расслоения и некоторым общим данным типа численности населения, среднедушевых доходов на местах и т.п. получить необходимый для более высокой ступени новую, более общую меру расслоения. Если это так, то немедленно порождается целый ряд задач:

1) как должна зависеть функция от доходов и их долей, чтобы ее можно было назвать коэффициентом (мерой) расслоения,

2) какой должна быть функция от всех местных мер, чтобы

3) функция от любого числа местных мер и, скажем, численностей людей и средних доходов на местах была бы опять мерой расслоения всего населения;

4) может ли быть эта функция взвешенной суммой местных мер с добавлением слагаемого лишь от общих данных, при этом

5) веса зависят только от последних и т.п.

Какими свойствами должна обладать функция от наблюдаемых доходов, чтобы ее можно было назвать показателем расслоения? Некоторые из свойств уже были упомянуты, однако они были расплывчаты и общи, поэтому попробуем конкретизировать их с тем, чтобы они дали возможность получить желаемые функции. В первую очередь все меры расслоения или неравенства должны обладать свойствами того, что мы вкладываем в понятие расслоения (неравенства). Разделим все замеченные на сегодняшний день свойства на три крупные группы. К первой отнесем общие свойства, без которых нет представления о неравенстве доходов и расслоении. Ко второй группе относятся свойства неравенства (расслоения), которые должны быть присущи и показателям наших представлений них. Наконец, последняя, третья группа содержит свойства лишь отчасти принадлежащие расслоению, но без которых пока нельзя обойтись при математическом выводе вида функции от доходов. Часто последние называют чисто техническими и они не будут даже приведены далее, хотя для простоты доказательств теорем без них нельзя обойтись.

Свойство симметрии. Рассмотрим для простоты лишь доходы w₁ , w₂ , ¼ ,w_n , получаемые каждым из n членов группы или общества, и допустим, что все они (доходы) не равны друг другу. Довольно очевидно, что наше представление о расслоении не должно зависеть от того порядка, в котором приведены эти доходы в списке, т.е. любая перестановка людей вместе с их доходами не будет менять нашего представления о расслоении или неравенстве в группе (обществе). Такое свойство неравенства обычно называют симметрией, оно должно быть и у показателя расслоения. Это свойство говорит о том, что при расчёте меры расслоения имеют дело не с вектором, а всего лишь со множеством доходов. Обозначим его w , а функцию от этого множества J(w ) .

Условие 1 (симметрии) . Функция J от множества доходов w может быть показателем расслоения, когда она не зависит от их упорядочения.

Элементом множества w может быть, конечно, не только доход, т.е. число, а целый набор, характеризующий благосостояние данного человека. Далее будет существенным лишь то, что в для каждого элемента определено понятие близости и, следовательно, понятие центра, т.е. элемента, не обязательно принадлежащего самому множеству w , наиболее близкого ко всем точкам w_i . Таким образом, само множество принадлежит пространству, в котором определена близость точек.

Наиболее часто в качестве центра используют среднее значение всех точек множества w . Таким образом, для пространства, из которого взято множество, определены операции сложения и умножения на число. Более того, в частности, общество может состоять из нескольких групп - множеств, поэтому множества точек - групп могут быть объединены, т.е. в пространстве определена операция объединения множеств. Далее требования к пространству, к которому принадлежат точки – благосостояния отдельных людей - будут уточняться.

Свойство повторения. Допустим, что людей некоторого общества можно разбить по благосостоянию или доходам, эти два термина употребляются как синонимы, на две или более групп так, что каждая группа будет полным повторением и по числу и по благосостоянию людей некоторой исходной. Ясно, что при таком предположении расслоение всего общества и каждой его группы должно быть одним и тем же. Поэтому этому свойству неизменности при повторении, которым обладает само расслоение, должен удовлетворять и показатель.

Условие 2 (повторения) . Функция от объединения r одинаковых множеств может быть показателем расслоения, если она инвариантна по отношению к умножению множества на число, J(rw ,rn)=J(w ,n) при r>0 .

В последнем соотношении введено новое обозначение: w _i =rw , если все w _i =w . Кроме того, при обозначении функции был добавлен аргумент n , чтобы учесть вес множества. Весом каждого из объединяемых множеств, особенно в случае, когда количество элементов (людей) в них не равно друг другу, может служить, например, число точек во множестве (т.е. число людей в группе). Когда общество состоит из нескольких групп, численности которых n_i , то величина n_i может служить мерой группы.

В последнем случае мерой всего общества может служить n= S _i n_i . Теперь из условия повторения получается, что расслоение не зависит от количества людей, следовательно, и общество и его группы можно “стандартизовать”, разделив на их численность. Отсюда вытекает, что функция может не зависеть от n , но тогда вместо множества w и его элементов w_i следует использовать их меру, которой после стандартизации будет вероятностная. В этом случае мерой группы в обществе будет n_i /n= l _i , мерой P(w ) элемента w во всем обществе будет смесь мер P_i (w ) всех составляющих его групп, т.е. P(w )= S _i l _i P_i (w ) . Вместо вероятностной меры P далее почти всегда будет использоваться функция распределения F , так как пространство благосостояний (доходов) имеет отношение порядка p (<) , т.е. F(w)=P(w p w) .

Первые два свойства расслоения имели, как оказалось, малое отношение к самому расслоения, они скорее описывали само общество и его группы. Поэтому далее обозначения (w ,n), (F,n) и F эквивалентны.

Из последних двух свойств расслоения следует вывод. Расслоение P ( w ) как функция множества w представляет собой функционал от вероятностной (как, впрочем, и любой конечной) меры F множеств. Действительно, эта мера не меняется от перестановок и повторения. Наконец, объединение нескольких множеств можно отождествить с со смесью вероятностных мер каждого из них с вероятностями, пропорциональными их весам (числу элементов, доходам). Кажется очевидным, что при объединении различных по доходам множеств (групп) людей расслоение вновь получившегося общества будет не убывать, а увеличиваться

Условие 3 (монотонности) . Значение функции J от смеси двух (или более) не одинаковых вероятностных мер не убывает по сравнению с ее значениями от любой из исходных.

Далее, наряду с уже введенным обозначением J(w ,n) , будем использовать новое - J(F) (J(F,n)) , где F вероятностная мера множества w . Более того, для простоты, F - функция распределения) доходов, так как последняя показывает и величину дохода (точка роста) и численность людей получающих эти доходы (величина скачка в точке роста, умноженная на n ) в обществе F и F_i в его группе i .

Свойствами монотонности и нормировки открывается вторая группа свойств расслоения, поскольку первые два свойства относились скорее к описанию характеристик общества, чем к его расслоению. В группе, состоящей из одного человека, имеющего какой-либо доход, расслоения нет, в полном соответствии с нашим представлением о расслоении. В группе, в которой все доходы входящих в нее людей делятся по мере надобности на каждого, по-видимому, расслоения также нет, как и в группе, где все люди имеют один и тот же доход. Функция, соответствующая показателю расслоения должна отражать и это.

Условие 4 (нормировки) . Если функция распределения F вырождена, т.е. имеет скачек, равный 1 в какой-либо одной точке, то J(F)=0 .

Действительно, можно предположить более простое: J(w ,1)=0 . Тогда в силу условия повторения имеем при r=n условие нормировки 4. Примером группы, где суммарный доход распределяется по потребности (коммунистический принцип) может служить семья, домохозяйство, скит или монастырь, поэтому условие нормировки не представляется чем-то неожиданным или невозможным.

Теперь из условий 3 и 4 следует, что J(F, n ) ³ 0 для любых F . Если учесть ещё и условие 2, то получим, что число n в обозначениях J ( F , n ) можно опустить и писать просто J ( F ) .

Свойство непрерывности. Может ли расслоение ярко выражено меняться при сравнительно малом изменении дохода в отдельной группе или у одного человека, которые в свою очередь несколько меняет вид функции распределения F ? Ответ на этот вопрос ясен - расслоение при малом изменении дохода у кого-либо настолько незначительно, что не чувствуется. Таким же свойством должен обладать и показатель J(F) . Отсюда следует, что показатель расслоения представляет собой функционал от функции распределения доходов.

Условие 5 (непрерывности) . Функционал J(F) непрерывен.

Свойство сравнимости. При сравнении расслоений в разных странах, хотя там доходы могут быть измерены в разных денежных единицах, должно быть ясно, где неравенство больше, а где меньше. Поэтому у представления о величине расслоения или неравенства нет зависимости от единицы измерения дохода. То же самое должно быть свойственно и функции J .

Условие 6 (однородности) . Функция J(F(w)) инвариантна по отношению к масштабу измерения дохода w , т.е. однородна степени 0 по w .

Свойство передачи в проблему мер неравенств было введено Пигу и Дальтоном, что часто подчеркивается названием: свойство Пигу-Дальтона. Оно состоит в том, что от передачи сколь угодно малого количества от более богатого к менее богатому показатель неравенства убывает. Это же свойство можно сформулировать и в обратной форме. Если группа с равными доходами распадается на две с неравными при тех же суммарных доходах, которые были до распадения, то расслоение не может уменьшиться. Последнее свойство настолько важно, что оно встретится далее, но будет названо там свойством стремления к одинаковости.

Условие 7 (передачи) . От расщепления какой-либо группы, задаваемой F , на две, например, F₁ и F₂ (или более) групп функция J(F) ³ max[J(F₁ ),J(F₂ )] .

По сути, последнее условие мало добавляет к уже приведенным условиям повторения и монотонности, так как уточнилась лишь формулировка - появился функционал от смеси двух аргументов, вместо функционала от одного. В самом деле функции распределения F ₁ иF ₂ присутствуют и в правой и в левой частях неравенства, так как функция F= l F₁ +(1 -l )F₂ , где l Î [0,1} и F ₁ ¹ F ₂ . Возникает вопрос, нельзя ли функционал от смеси двух аргументов представить в виде смеси функционалов от каждого. Такое представление полезно из-за возможности сильно облегчить расчет, который такое оно позволило бы осуществить. Однако последнее высказывание относится уже не только к свойствам расслоения и его показателей, а скорее к методу расчета самого показателя расслоения.

Действительно, если речь идет о стране, состоящей из ряда районов, то для расчета меры неравенства в ней после уже сделанных расчетов коэффициентов расслоения в каждом районе необходимо знать функцию распределения F для всей страны, хотя она - смесь функций распределения F_i для каждого района i . Для этого следует передать из всех районов доходы всех людей, из совокупности которых получается функция F для всей страны. А можно ли ограничиться только “сжатой” информацией, например, о средних доходах в районах, самих мерах расслоения и еще о чем-либо? Примеры, показывающие такую возможность, имеются - это так называемые неразложимые смеси функций распределения и достаточные статистики для последних.

Свойство восстановления расслоения всего общества по смеси расслоений в его группах очевидно, поэтому очень полезно иметь и возможность пересчета функционалов (мер неравенства) от смеси по “сжатым” данным о коэффициентах расслоения в отдельных частях. Отсюда появляется следующее предположение о способе пересчета.

Условие 8 (разложимости) . Функционал J(F) может считаться разложимым в том случае, когда он имеет вид J(F)=[ m (F_i )]J(F_i )+J(F₀ ) , где p[ m (F_i )] -весовая функция, зависящая от центров m (F_i ) групп i, (i=) и, кроме того, F_i -функции распределения доходов в группах, а F₀ - функция распределения центров групп, число которых m .

2. Показатели расслоения

Условие разложимости - это определение разложимого функционала J : функционал J называется разложимым, когда он, после подходящего монотонного преобразования, может быть представлена в виде уже приведенной суммы, где F₀ - смесь функций распределения F_i в группах . В этом определении сразу дано такое представление функции J , которое могло бы быть дано в два этапа, первый - определение разложимости как некоторой зависимости от функций распределения в группах и на их центрах, и второй - приведение к аддитивной зависимости после монотонного преобразования. Если далее определить показатель (или меру) расслоения (или неравенства) I как разложимый функционал J , удовлетворяющую условиям 1-7, то может быть доказана следующая теорема.

Теорема . Непрерывно дважды дифференцируемая разложимая мера расслоения удовлетворяет условиям передачи и однородности тогда и только тогда, кода она имеет вид

для некоторого a ³ 0, где m (F) - центр распределения F , а w_a ( x ) - решение уравнения x ( d ² w ( x )/ dx ² )+(1- a )( dw / dx )= b .

Если учесть, что решения w(x) дифференциального уравнения xw”+(1 -a)w’=b и соответствующие им p(F_l ) имеют вид

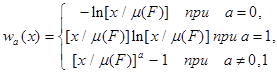иp_a (F_l )=[l/ m (F)]^a ,

то общим видом показателя расслоения будет следующий

.

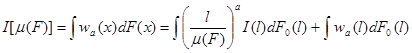Смешивающая функция для дискретных величин F ₀ ( l ) в точке l = m ( F_i ) имеет скачёк величины l _i , для непрерывного случая аналогично.

Результат теоремы состоит, во-первых, в том, что мера расслоения не зависит от численности общества (или групп), а зависит лишь от функции распределения. Во-вторых, характеристических (существенных) свойств всего два - однородности и передачи.

Все остальные следуют из них. Таким образом, не было необходимости приводить и описывать все свойства расслоения, хотя они многое проясняют. Более того теорема показывает, что меру расслоения можно искать в виде и функция w(x) связана с множеством решений уравнения xw”(x)+(1 -a)w’(x)=b .

3. Частные показатели

Осталось привести лишь частные случаи. При a =0 имеем

I ( F )= ,

при a=1 получается мера расслоения Тайла (Theil):

I(F)= ,

наконец, при a=2 имеем квадрат коэффициента вариации:

I(F)= ,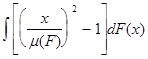

множители перед интегралом опущены в соответствии с определением разложимости.

Рассмотрим общество, заданное функцией распределения F , состоящее из m групп, каждая из которых определяется своей функцией распределения F_i (). В этом случае F= , где l _i ³ 0 , и Sl _i = 1. Кроме того, чтобы F была функцией распределения всего общества необходимо представление распределения центров групп в виде F₀ (x)= S_i H(x -x_i ) l _i , где H(x) - функция Хевисайда, т.е. она равна 1 при x ³ 0 и 0 в других случаях, а l _i =n_i /n и x_i = m (F_i ) .

Остается привести лишь разложения уже приведенных показателей расслоения.

Для первого показателя - логарифмической меры расслоения - имеем функцию w(x) =-ln[x/ m (F)] , которая дает название меры. Для нее весовая функция p имеет вид p[ m (F_i )]=1 . а показатель расслоения

I[ m (F)]= ,

или, в более общем виде для распределения F(x)= , где F(x/l)=F_i (x) при l= m ( F_i ) ,

.

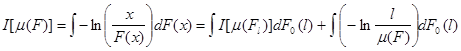Для меры неравенства Тейла функция w(x)=[x/ m (F)]ln[x/ m (F)] , весовая функция p[ m (F_l )]=[l/ m (F)] , поэтому,

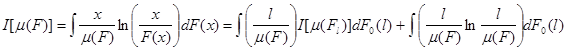
Для квадрата коэффициента вариации функция w(x)=[x/ m (F)]² -1 , весовая функция p[ m (F_l )]=[l/ m (F)]² и

.

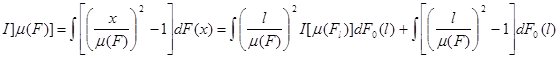В самом общем виде для функции w(x)=[x/ m (F)]^a -1 весовая функция p[ m (F_l )] будет равна [l/ m (F)]^a , а разложимый показатель расслоения для любого a имеет вид

.

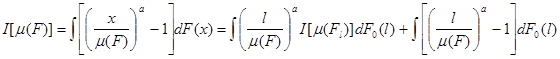Для того, чтобы убедиться в неотрицательности любого из приведенных показателей бедности следует проделать следующее. Во-первых, все представленные в показателях расслоения весовые функции w ( x ) выпуклы. Во-вторых, все функции распределения F_l таковы, что их средние значения равны единице. В-третьих, для выпуклых функций w справедливо неравенство Йенсена E w ( X ) ³ w ( E X ) . Теперь, применив неравенство Йенсена к весовой функции w [ x / m ( F )] получаем требуемый результат.

Последнее обстоятельство, на которое необходимо обратить внимание, заключается в том, что функция Лоренца разложима в смысле уже данного определения. Действительно, пусть F ( w )= S l _I F_i ( w ) . Тогда справедливо равенство L ( w )=(1| W ) S l _i W_i L_i ( w ) , которое следует из определения функции Лоренца после вынесения из-под знака интеграла S l _i и умножения каждого слагаемого на W_i / W_i . Легко убедиться, что сумма весов ( l _I W_i / W ) последнего соотношения равна 1. Однако коэффициент Джини неразложим. Наконец, энтропия распределения, представляющего собой функцию Лоренца, это разложимая мера расслоения Тейла.

ЗАДАЧИ

1. Получите с помощью таблицы из приложений к гл. 3 логарифмическую меру расслоения.

2. Получите с помощью таблицы из приложений к гл. 3 меру расслоения Тейла.

3. Получите с помощью таблицы из приложений к гл. 3 меру расслоения, основанную на квадрате коэффициента вариации.

Справки и ссылки

Глава базируется в основном на известных работах о разложимых показателях Fracois Bourguignon’а и Antony F.Shorrocks’а. В этих работах, по-видимому, впервые был поставлен вопрос о показателях со свойством разложимости. Само это свойство было подмечено ранее, как


10-09-2015, 16:08