канд. биол. наук М.П.Иванов, д-р техн. наук В.В.Кашинов
ФНИИ им.А.А.Ухтомского, СПбГУ
Введены континуально многозначные функции, позволяющие адекватно описывать физические задачи. Показано их отличие от разрывных функций. Сформулирована и решена вариационная задача для функционалов с разрывным интегрантом, зависящих от линейных интегральных операторов, действующих на искомую оптимизируемую функцию, причем ядро оператора и оптимизируемая функция могут быть континуально непрерывными. С помощью таких операторов можно адекватно описывать распределенные частицы.
Хорошо известный в физике принцип наименьшего действия [1] основан на классическом вариационном исчислении, когда функционал зависит от экстремали и ее производных, применим только для нейтральных частиц. В заметке [2] показано, что для заряда ускорение запаздывает по отношению к возмущающей силе за счет лоренцевых сил трения, т.е. для заряда существует некоторая переходная импульсная характеристика, а движение заряда можно описать интегральным оператором. Поэтому для зарядов, когда нельзя связать значение ускорения в данный момент со значением возмущения в тот же (или другой) момент, принцип наименьшего действия неприменим. Для таких задач требуется другой математический аппарат. Обобщенный принцип наименьшего действия основан на методах обобщенного вариационного исчисления. Рассмотрим его.
1. Континуально многозначные функции
В последнее время негладкие, разрывные и сингулярные функции стали привлекать внимание [3-5]. Построен пример непрерывно дифференцируемой разрывной функции на пространстве D - бесконечно дифференцируемых финитных функций [4]. При решении вариационных задач экстремалями иногда оказываются негладкие, т.н. разрывные или сингулярные функции [3, 5]. Однако понятие разрывности функций в точках разрыва) не всегда соответствует физическим и математическим объектам - непрерывным кривым, которые они фактически описывают.
Рассмотрим кривую - прямоугольный импульс (рис. 1), определенный и непрерывный на всей оси абсцисс. Подобные объекты можно представить не только математически: например, так можно представить разложенную на плоской поверхности веревку. Но если про прямую b мы говорим, что она существует, и пишем 
при
, то про точки x=0 и x=1 говорится, что в них функция терпит разрыв первого рода, а прямых a и c как бы нет, хотя веревка физических разрывов не имеет.
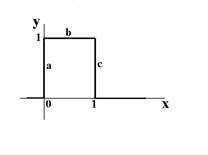
Рис.1. Непрерывная кривая - прямоугольный импульс
По-видимому, объясняется это тем, что рассмотрения многозначных функций традиционно стараются избегать. В нашем же случае точкам x=0 и x=1 соответствуют замкнутые отрезки [0,1], параллельные оси ординат, т.е. одной точке на оси абсцисс соответствует множество точек на оси ординат, имеющее мощность континуума. Получается не просто многозначность, а многозначность мощности континуума.
Рассмотрим характерный пример - первую введенную в физике разрывную функцию - функцию Хевисайда, которая определяется [6-8] как предел последовательностей непрерывных функций, имеющих все производные. Поэтому график предельной функции вроде бы должен быть непрерывным. Этому противоречит определение функции Хевисайда, данное, например, в монографиях [6-8],
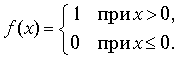(1.1)
Введем уточненное определение функции включения, соответствующее предельному переходу в эквивалентных последовательностях [6] непрерывных функций, имеющее непрерывный график,
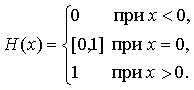(1.2)
Если функцию включения (1.2) можно представить в виде непрерывной веревки, разложенной на плоской поверхности, то функция Хевисайда представляется той же веревкой, из которой вырезан кусок (сегмент [0,1]) в точке x=0. Обе функции имеют равные односторонние пределы, но разные графики при x=0 и вытекающие из этого свойства.
На первый взгляд, определение (1.2) непривычное, но фактически оно не новое. Когда говорят о значении определенного интеграла от положительной подынтегральной функции, то имеют в виду, что он "равен площади криволинейной трапеции, ограниченной графиком подынтегральной функции, осью абсцисс и прямыми, параллельными оси ординат, построенными на концах отрезка интегрирования" [8].
Поскольку определенный интеграл в конечных пределах от a до b всегда можно выразить с помощью сдвинутых функций включения H(x) через интеграл с бесконечными пределами
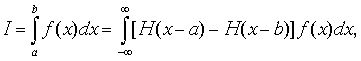(1.3)
то функции включения (1.2) как раз и описывают "прямые, параллельные оси ординат", чего не скажешь о функции Хевисайда (1.1).
Замечание. Из формулы (1.3) следует, что все интегрируемые функции фактически определены на всей оси абсцисс, что позволяет, обладая методикой решения разрывных экстремальных задач, например, приведенной в монографии [5], легко решать их, когда экстремум не внутренний, а достигается на границе замкнутого отрезка [a,b].
Используя определение функции включения (1.2), функцию, изображенную на рис.1, - прямоугольный импульс - можно записать:
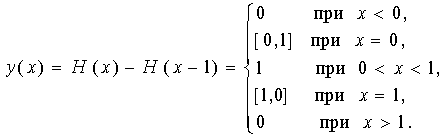
Предложенное непротиворечивое определение непрерывной функции включения позволяет адекватно описывать непрерывные кривые в точках математической разрывности. Сам термин "разрывная функция" выбран несколько неудачно. Фактически мы имеем дело с непрерывными функциями, обладающими многозначностью мощности континуума. Действительно разрывными являются функции типа функции Хевисайда (1.1), но фактически, когда говорится о "разрывных функциях", в большинстве случаев имеются в виду функции вида (1.2).
Интересно отметить, что популярные пакеты компьютерных программ для решения прикладных задач и построения графиков EUREKA и MATHEMATICS дают графическое изображение функции включения, записанной как H(x)=(1+sgn(x))/2, именно в виде формулы (1.2). В монографии [5] в графиках также используется непрерывная функция включения (1.2), хотя это определение и не приводится.
Наглядное представление d -функции в виде обычной функции в математической литературе отрицается, поэтому при решении экстремальных негладких и разрывных задач понятие d -функции не используется [3, 5]. Для аналитического решения экстремальных задач требуется уточнение определения в d -функции.
Для уточнения определения введенной Дираком сингулярной функции - d -функции введем d -образную эквивалентную последовательность [6, 9] через функции включения (1.2)
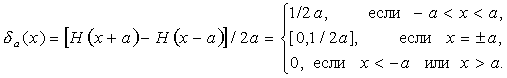(1.4)
При любом значении a существует интеграл
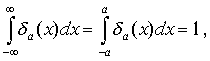
и предел формулы (1.4) при a- 0 является d -функцией, т.е.
(1.5)
Так определенная (1.4)-(1.5) d -функция является пределом непрерывного графика прямоугольного импульса высотой 1/2a и шириной 2a. При a- 0 высота "стенок" прямоугольного импульса неограниченно возрастает, а ширина импульса стремится к 0. В пределе "стенки" "слипаются" в один луч - d -функцию, расположенную в начале координат.
При прохождении функции в d a
(x) по направлению кривой от 
к 
"стенки" прямоугольного импульса проходят в противоположных направлениях, поэтому d -функция (состоящая из двух "слипшихся" "стенок") одновременно направлена в противоположных направлениях. (Одну кривую, которую проходят в разных направлениях, считают различными кривыми [8]).
Определенная выше d -функция имеет наглядное представление в виде луча - положительной полуоси ординат. Имея бесконечную высоту и нулевую ширину, d -функция ограничивает единичную площадь (неопределенность типа
) и обладает двойной направленностью.
Следует отметить, что в приведенном определении d -функция не рассматривается как "равная нулю при всех 
и обращающаяся в точке x=0 в бесконечность" [8]. Теперь d -функция рассматривается как луч - линейное множество, имеющее мощность континуума.
Поскольку уточненное определение d -функции не затрагивает ее определения как функционала на пространстве D, все свойства d -функции, рассматриваемой как сингулярная обобщенная функция, сохраняются.
Производная d -функции 
имеет наглядное представление в виде оси ординат, обладает двойной направленностью в каждой из полуплоскостей y<0 и y>0 и пересекает ось абсцисс (все это в одной точке x=0).
Далее все производные понимаются в обобщенном смысле [6-9], т.е. в виде свертки с производными сингулярной d -функции.
Теория обобщенных функций и разработанная техника вычислений их производных [6-9] позволяют распространить необходимые условия экстремума на континуально многозначные (так называемые разрывные) функции многих действительных переменных.
2. Вариационные задачи с разрывным интегрантом
Многие прикладные оптимизационные задачи сводятся к поиску экстремумов интегральных функционалов с разрывным интегрантом. Здесь "разрывной" понимается так: не обязательно разрывной. Обычно, в том числе и в монографиях [3, 5], оптимизационные задачи рассматриваются для функционалов, зависящих от операторов дифференцирования. В работах [10, 11] рассматриваются функционалы, зависящие от интегральных операторов, что существенно расширяет круг решаемых задач.
Будем решать вариационную задачу для функционалов с разрывным интегрантом, зависящих от линейных интегральных операторов
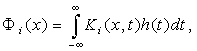(2.1)
где h(t) - экстремаль, относительно которой предполагаем, что
.
Функционал качества I может зависеть от нескольких операторов
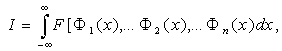(2.2)
где F[T ]- интегрант, определяющий связь (композицию) операторов F i в функционале I. Интегрант F[T ] может быть непрерывным, гладким, негладким и даже континуально многозначным или разрывным.
Оптимизации методами негладкого анализа посвящена монография Френка Кларка [3], но методику Кларка применить к функционалам, зависящим от интегральных операторов, нельзя, как нельзя ее применять и для функционалов с континуально многозначным или разрывным интегрантом. Кроме того, экстремали у Кларка предполагаются абсолютно непрерывными. Все это несколько сужает область применения негладкой оптимизации Кларка - теории, впитавшей в себя достижения его предшественников, на кoторых он ссылается в своей монографии. Поскольку оптимизируемый функционал зависит от интегральных операторов, метод, использованный в монографии [5], неприменим тоже. В то же время для решения сформулированной задачи достаточно методов вариационного исчисления, теории обобщенных функций и теоремы Фубини [8], поэтому будем поступать так.
Негладкий, континуально многозначный или разрывной интегрант можно представить с помощью функции включения H(x) (1.2) или ее производных, т.е. d -функции (1.5) и ее производных, используя их фильтрующие свойства. При варьировании функционала I все производные будем понимать в обобщенном смысле
.
Заметим, что этот интеграл теперь имеет математический и физический смыл, а не является "просто символом", как при классическом определении d -функции.
По общему правилу [9-12] введем однопараметрическое семейство кривых 
, где d h(t)-произвольная функция из Lp
[a,b], a - малый параметр. Подставляя 
в операторы (2.1), а операторы (2.1) в функционал (2.2) и дифференцируя I по a , получим вариацию функционала d I и приравняем ее нулю:
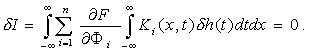(2.3)
Теперь, чтобы получить необходимое условие экстремума, надо исключить произвольную функцию из вариации функционала d I. В классическом вариационном исчислении это делается с помощью интегрирования по частям, которое в данном случае неприменимо. Полагая, что к вариации d I применима теорема Фубини [8], одним из условий применимости которой может быть суммируемость произведений
изменим в формуле (2.3) порядок интегрирования [10, 11]
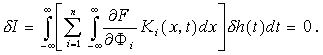(2.4)
Используя основную лемму вариационного исчисления в формулировке Л.Янга [7], получим аналог уравнения Эйлера для функционалов с континуально многозначным или разрывным интегрантом, зависящих от линейных интегральных операторов, действующих на экстремаль,
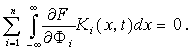(2.5)
Следствие. Если воспользоваться фильтрующим свойством d -функции и ее производных, и обозначить ядра операторов (2.1) через Ki (x,t)=d (i) (x-t), то уравнение (2.5) примет вид уравнения Эйлера
(2.6)
простейшей вариационной задачи [12], но для функционалов с континуально многозначным или разрывным интегрантом
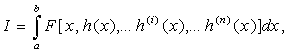(2.7)
зависящих от искомой функции h(t) и ее производных h(i) (t).
Пример. Задача Дидоны с канавой. В распоряжении царевны имеется веревка заданной длины L, которой следует ограничить участок побережья, причем береговая черта представляется линией x=0 на плоскости Оtx (Рис.2). При этом надо найти кривую длины L, лежащую в полуплоскости
, соединяющую точки (-1,0) и (1,0), такую что площадь между кривой и осью t максимальна.
Стремясь иметь для примера негладкий интегрант, Кларк модифицировал [3, с.178] задачу Дидоны следующим образом. Он полагает, что для некоторого a >0 земля в области x>a худшего качества и доход с нее составляет только половину дохода с земли в области x<a .
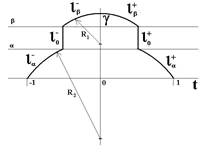
Рис.2. Участок Дидоны с канавой
Доход Д с огороженного участка, ограниченного кривой x(t), равен
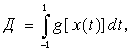(П.1)
где gn
[x(t)] = {x(t), если
; (x+a )/2, если 
} .Следует максимизировать значение дохода Д (интеграла (П.1)) при наличии ограничений
(П.2)
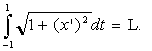. (П.3)
Далее Кларк использует методы негладкого анализа для решения модифицированной задачи Дидоны. Применение этих методов ограничивается негладкими интегрантами и абсолютно непрерывными экстремалями.
Для частичной иллюстрации возможностей предложенного нами метода решения задач с разрывным интегрантом будем полагать, что участок Дидоны параллельно береговой линии пересекает канава шириной b -a . Один берег канавы проходит по линии x(t)=a ., а другой - по линии x(t)=b . Участок канавы, ограниченный берегами и веревкой (рис.2), никакого дохода не приносит, и интегрант выглядит так:
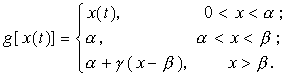(П.4)
Веревка ограничивает канаву, пересекая ее, но разорвать веревку Дидона не может, поэтому изопериметрическое условие (П.3) остается в силе. Требуется максимизировать доход с участка, расположенного по берегам канавы, ограниченного береговой линией и веревкой.
Представим g[x(t)] с помощью единичной функции включения (1.2) в виде
В уравнение Эйлера простейшей вариационной задачи (2.6) входят производные интегранта по x и по
. Вычислим эту производную
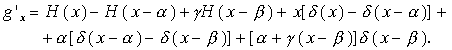
Производя сокращения и учитывая свойства d -функции [7], находим
или
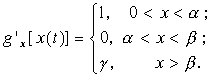(П.5)
С учетом изопериметрического условия (П.3), получим дифференциальное уравнение для экстремали
(П.6)
где l - неопределенный пока множитель Лагранжа [7].
Уравнение (П.6) при 
и ограничениях (П.2) имеет интегралом окружность
(П.7)
где C = ¦ (l 2 /a2 -1)1/2 , симметрично расположенную относительно оси Оx (рис.2). Выразим длину веревки Дидоны через параметры задачи a , b , g и неизвестный коэффициент l .
В горизонтальной полосе 0<x<a 
и центр соответствующей окружности располагается ниже оси Оt (иначе интегральные дуги 
окажутся вне вертикальной полосы -1<t<1), откуда для длины 
дуги получим
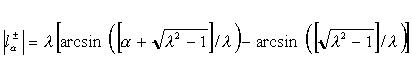(П.8)
При x>b и 
при отыскании максимума функционала (П.1) в случае g >1 (или g <1) центр окружности, содержащей интегральную дугу
, будет расположен выше (или ниже) оси Оt. Для длины дуги получим
(П.9)
В полосе a <x<b 
и интегральная линия имеет вид отрезков прямой
, соединяющей концы дуг 
и 
с концами дуги. При разных значениях параметра g может быть разная ориентировка этих отрезков. В частности, они могут быть параллельны оси Оy (
)или наклонены. Длина отрезка 
определяется выражением
или
Заметим, что при a =b и 
лишь при g =1, т.е. требования "стыковки" или даже "сопряжения" дуг 
и, наложенные в [3] при
, не вытекают из условия задачи, несмотря на неразрывность веревки.
Окончательно получим
или (П.10)
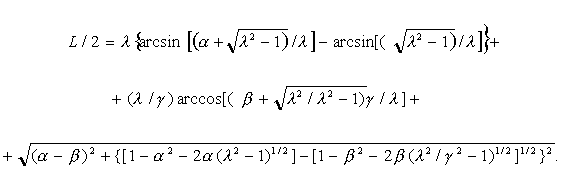
При a = b получаем
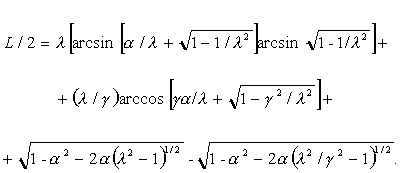
При a = b и a = 1 получается длина дуги в классической задаче [12] Дидоны
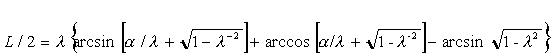
Или
(П.11)
3. Вариационная задача поиска оптимального оператора
Кроме приведенной в разделе 2 постановки вариационной задачи, сформулируем задачу поиска ядра оптимального оператора F i , действующего на заданные функции Si , и доставляющего экстремум функционалу с разрывным интегрантом F. Такие задачи могут, например встречаться при нахождении распределения плотности заряда в частице.
Пусть существует функционал I с разрывным интегрантом F
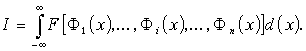(3.1)
В случае конечных пределов интегрирования в (3.1) функционал I всегда можно выразить через интеграл с бесконечными пределами с помощью функции (1.2) включения H(x). В формуле (3.1) символами F i (x) обозначены линейные интегральные операторы
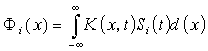(3.2)
с искомым ядром K(x,t), действующим на заданные функции
,
.
Частные решение
Установим интересное свойство множества экстремалей. Для этого представим ядро в виде произведения
(3.3)
где
, - выбранная из некоторого множества произвольная функция, на которую умножаются входные процессы Si
(t);
, - разностное ядро, которое требуется найти из условия экстремума функционала I. Подставив (3.3) в (3.2), получим
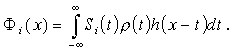(3.4)
Используем свойство свертки и приведем оператор (3.4) к виду
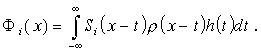
29-04-2015, 02:01