Реферат
на тему:
"Распределения и меры расслоения доходов"
Москва, 2008
Введение
Душевой доход, как уже стало ясно, варьирует довольно значительно, поэтому во всех странах стараются иметь сравнительно малые доходные группы (слои) с доходами, скажем, от 200 до 300, от 300 до 400 и т.д. и основную роль начинает играть доля людей, принадлежащих к каждой из них. Поэтому изучение вопросов распределения членов общества по доходам (или доходов по людям) имеет богатую историю и много граней. Но далее будет рассматриваться лишь один аспект этой большой проблемы: каково расслоение общества и какова мера этого расслоения. Часто вместо термина «расслоение» употребляют аналогичные, например, «дифференциация», «рассеяние» и даже «неопределенность» доходов или термины противоположного смысла, скажем, «концентрация», «сосредоточение», «определенность» и т.п.
1. Меры расслоения
Из ранее сказанного ясно, что мера расслоения должны быть тесно связаны с долей людей, имеющих доход меньший x рублей. Эта доля изучается теорией вероятностей и обычно там обозначается F(x) . Кроме того, мера расслоения должна удовлетворять некоторым требованиям:
1. Мера расслоения минимальна, когда доходы всех людей одинаковы (расслоения нет);
2. Мера расслоения увеличивается при увеличении разброса доходов;
3. Мера расслоения не зависит от единицы измерения доходов.
Требование 1 выполняется тогда, когда при одинаковых доходах значение меры минимально (удобнее, когда оно равна 0). Тогда мера расслоения положительна и тем больше, чем больше отличаются доходы разных людей друг от друга.
Наиболее полно меры расслоения изучаются теорией вероятностей, где обычно говорят не просто о мерах расслоения, а о рассеянии. Мерой рассеяния в теории вероятностей служит энтропия E распределения F(x) , которая задаётся так:
E= -M lnF’ ( x )
где x
– случайная величина, распределенная по закону F(x)
. Для случайных величин, душевых доходов отдельного человека, на которого в домохозяйстве приходится x1
, x2,
…,
или xn
денежных единиц, с вероятностями p1
, p2
,…, pn
(
)
, энтропия E
вычисляется с помощью следующего соотношения:
Для непрерывных случайных величин, имеющих плотность f(x)=F’ (x),
энтропия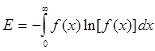 
.
Очевидно, что для дискретных случайных величин энтропия E удовлетворяет неравенству 0 £ E £ Em , где Em – максимальное значение энтропии. Распределение, соответствующее Em , можно найти, как впрочем, можно найти и распределения, соответствующие другим мерам расслоения.
2. Примеры
Пример 1. Рассмотрим доходы xi =a+(i ‑1) h , где a – минимальный доход, а h – шаг дискретности, скажем, равный денежной единице. Если среднедушевые доходы ограничены величиной b , то всего градаций доходов будет n , где n=m+1, а m=(b -a)/h , т.е. x1 =a , x2 =a+h , x3 =a+2h, …, xn =b . Если верхнюю границу указать трудно, то будем считать, что последовательность x1 , x2 ,…, xn ,… не ограничена. Пусть каждому xi соответствует вероятность pi (доля людей, имеющих среднедушевой доход, равный xi ) .
а) Доходы ограничены и нужно найти такие pi
,
чтобы 
достигала максимума. Очевидно, что
. Таким образом, получена задача на условный экстремум. После дифференцирования функции Лагранжа 
по pi
имеем систему уравнений – lnpi
-1-l
. Откуда получаем, что pi
=e-1-
l
, т.е. одинаковы для любого i
. Из уравнения 
получаем выражение lnn
‑1-l
=0
для величины l и l=
lnn
‑1
, следовательно, pi
=e-1-
ln
n
+1
=e-
ln
n
=1/n
. Теперь легко получить, что в этом случае, когда все величины доходов равновероятны, Em
=
lnn
.
б) Банковские проценты, под которые можно вложить свой капитал, если они вполнеразумны, не поддаются обоснованному ограничению сверху. Но в этой ситуации, как правило, заданы минимальные проценты – r
, а также среднее значение всех процентов – b
. Теперь появляется задача: найти такие pi
,
которыедавали бы максимум 
при ограничениях 
и 
, где первые m
значений pi
=0
,а значения xi
=ih,
когда i=m, m+1,…
. С учетом всех ограничений функция Лагранжа будет равна
.
Принимая во внимание, что первые p1 , p2 ,… pm – равны 0 , так как минимум процента r=hm=xm , то можно найти (см. задачу 1)
,
где 
.
В этом случае
=lnx
/(1
‑x
)
.
в) Рассмотрим задачу из пункта а) этого примера, но в качестве меры расслоения возьмем не энтропию, а дисперсию. Попытка решить задачу так же, как в пункте а) приводит к выводу, что экстремума внутри области (симплекса 
и 
) нет. Следовательно, задачу нужно решить на границе симплекса. Для простоты, рассмотрим какие-либо точки душевых доходов, x
(не обязательно =a
) c
, и y
(не обязательно =b
) и соответствующие им доли людей (вероятности) обозначим p
и q
, оставшиеся на остальные точки xi
вероятности обозначим через 
(g
=p+q
), т.е. 1
-g
=
. По сути дела задача свелась к следующей: пусть заданы три величины среднедушевого дохода x
£
c
£
y
, которые случайно выбранный из популяции человек имеет с вероятностями p
, (1
-g
)
и q
. В этом случае, дисперсия равна D=
x
2
p+
y
2
q+c2
(1-
g
)
– [
x
p+
y
q+c (1-
g
)]2
.
Можно показать (см. задачу 2), что
D = p (1 ‑p ) ( y -x )2 – (1 -g ) [2 y ( y -x )+ g ( y 2 -c 2 )+2 c ( xp + yq )].
Поэтому последнее слагаемое неотрицательно и оно равно 0
при p+q=1
, т.е. при 1
-g
=0. Отсюда следует, что maxD
=
p
(1
‑p
) (
b
-a
)2
при заданном p
, maxD
=
p
(1
‑p
) (
y
-x
)2
при заданных x
и y
и 
при всех (x
,
y
,
p
) свободных параметрах.
Рассматривать аналог пункта б) для дисперсий не имеет смысла, так любое распределение, имеющее математическое ожидание при несуществующей дисперсии дает ответ.
Замечание 1
к примеру 1б. Все выведенные распределения имеют непрерывные аналоги; так для пункта а) таким аналогом будет равномерное распределение на отрезке [a, b
]. Для пункта б) аналогом будет показательное распределение с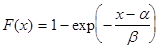 
и плотностью 
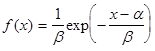, отличными от 0
при x
³
a
.
Замечание 2 к примеру 1б. Представляет интерес получить распределение с наибольшей энтропией не только при заданном среднем значении, но и заданной дисперсии. Для дискретного случая задача не решена, а для непрерывной случайной величины с неограниченным в обе стороны диапазоном ответ известен: распределение будет нормальным.
Пример 1 показывает, что всякое расслоение в том числе и в обществе из-за различных среднедушевых доходов можно мерить и дисперсией и энтропией, так как и та и другая мера равна 0 при равенстве среднедушевых доходов и растет при расслоении. Однако необходимо привести недостатки приведенных мер.
3. Свойства мер расслоения
Меры расслоения вводятся для того, чтобы иметь возможность сравнивать благосостояние разных обществ, или, говоря языком математики, разных распределений. При этом считается, что чем больше интуитивное представление о расслоении, тем больше и мера. Например, если расслоения нет, то и мера должна быть минимальной (чаще всего, равной 0 ) и она должна возрастать при росте расслоения. И дисперсия и энтропия безусловно удовлетворяют этому условию.
Свойство, которое необходимо для любой меры расслоения, – это свойство зависимости от того увеличивается или убывает средний доход, приходящийся на одного человека. Ясно, что при увеличении среднего дохода и при прочих одинаковых условиях (например, дисперсия или разность между наибольшим и наименьшим доходами остается постоянной) расслоение в обществе должно убывать и, наоборот, при уменьшении среднего дохода расслоение должно возрастать.
Однако свойство независимости от сдвига, т.е. от добавления или уменьшения всех среднедушевых доходов xi на одну и ту же величину, которая увеличивает или уменьшает на нее же средний доход, присуще и дисперсии и энтропии, которые зависят лишь от отличных от 0 вероятностей (плотностей), а не от участка, где они равны 0. Поэтому энтропия и дисперсия не реагируют на сдвиг (прибавку или уменьшение) всех доходов на одну и ту же величину.
Но сравнение возможно, когда меры выражены в одних и тех же единицах, лучше всего когда они (меры) вообще не зависят от единиц измерения доходов, т.е. когда они безразмерны. Энтропия удовлетворяет такому условию, но дисперсия, как легко видеть, нет. Поэтому вместо дисперсии вводят коэффициент вариации 
, который уже безразмерен.
Кроме уже описанных мер расслоения существуют другие, отмеченные уже ранее в предыдущей главе. Примеры мер будут приведены в конце главы для различных распределений, но прежде всего, нужно выбрать распределения, экономически подходящие для этого.
4. Примеры распределений
Распределение примера 1, приведенное в пункте а), равномерное. Оно имеет в экономике широкое применение и будет далее использоваться, но только в непрерывном случае. Распределение пункта в) двухточечное. Оно отражает тот факт, что доходы бывают только двух видов: большие – b и малые – a . При этом число людей, имеющих b и a одинаково. Эта идеализированная ситуация мало соответствует реальному положению дел: обычно доля p людей с малыми среднедушевыми доходами a превосходит долю q людей с большими (b ). Для простоты изложения материала далее будут оставлены такие идеализированные двухточечные распределения, но с разными долями p и q .
Разница в обсужденных распределениях состоит в том, что при необходимости найти человека (или людей) с заданным и малым интервалом доходов поиск наиболее затруднен как раз при равномерном распределении, а не при двухточечном. Пусть p =99% (а q =1%) и надо отыскать человека с малыми среднедушевыми доходами, тогда практически первое же попавшиеся лицо будет иметь нужный доход (ошибка возможна лишь в 1% случаев). Для равномерного распределения ошибка может быть сколь угодно велика при поиске человека с заданным и очень малым диапазоном его доходов. Например, если диапазон нужных (желаемых для некоторых целей) душевых доходов составляет всего 1%, от b -a , то найти человека при равномерном распределении столь же трудно, как найти богатого при двухточечном.
Обсуждение пункта б) примера 1 требует более детального рассмотрения. Упростим задачу, считая, что новые доходы образуются из вкладов прежнего капитала x в акции, банковские счета и т.п. Тогда прирост доходов dx за время dt будет равен
x (1+ydt) – x
где y – процент от акций, банковских вкладов и т.п. При равных возможностях всякого человека относительный прирост доходов dx/x не зависит от первоначального капитала: он равен ydt и одинаков при любых стартовых условиях, и, как правило, очень невелик поскольку некоторые из y , несмотря на положительность, очень малы, но надежны, а остальные, которые не очень малы, недостаточно надежны.
Если хочется определить связь величин процента y и дохода x , нужно решить уравнение dx /x =ydt , т.е. lnx =yt . Последнее означает, что логарифмы доходов равны процентам. На самом деле эти проценты случайны (h ), но распределены по одному и тому же закону – это и означает одинаковость. Но тогда и сами доходы будут случайными (и равными, скажем, x ) и lnx =h (здесь и далее считаем, что t равно единице времени). Допустим, что случайные величины надежных процентов h ограничены снизу и трудно обосновать разумную верхнюю границу, хотя среднее значение M h существует и известно. Если вдобавок к тому процент h еще и наиболее трудно определим, то возникает предположение, что h подчинено закону из пункта б) примера 1. Таким образом, сам доход x =eh и его распределение F(x)=P( x <x) необходимо найти, когда G(y) =P( h <y) известно.
Рассмотрим для простоты непрерывный случай, когда G(y)
=1
‑exp
, где m
минимальное значение случайной величины h
, а M
h
– ее среднее значение. Тогда справедлива цепочка равенств: G
(
lnx
)=
P
(
h
<
lnx
)=
P
(
e
h
<
x
)=
P
(
x
<
x
)=
F
(
x
)
, из которой находится функция распределения F(x)
доходов x
по известной функции распределения процентов G(
·
)
.
F
(
x
)=
G
(
lnx
)
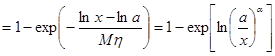
где a =1 /M h , а m= lna . Окончательно имеем функцию распределения F(x)=1 – (a/x) a доходов x ³ a , которая представляет собой распределение Парето.
Замечание 3. Если учесть, что доходность акций и банковских депозитов может быть не только положительной, но и отрицательной, например, из-за инфляции, то можно использовать замечание 2 к примеру 1б для получения распределения доходов по функции распределения доходности, как только что было сделано. В этом случае получится хорошо известное логнормальное распределение дохода, которое используется во многих исследованиях.
Во всех последующих примерах будут использоваться как стандартные параметры так и параметры, включающие минимальный (a) и средний доходы (W) .
Пример 1. Распределение Парето. Пусть распределение доходов w>0
имеет вид F(w)=[1
– (a/w)
a
]+
,
где [u]+
обозначает max (u, 0)
, а a
– минимальный доход. В этом случае для существования математического ожидания W=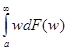
=a
необходимо, чтобы a
>1,
так как W>a
и a
=
. Тогда ордината кривой Лоренца y=L(w)
имеет вид L (w [1
– (a/w)=
=)
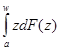a
-1
]+
,
а площадь l
под кривой Лоренца l=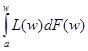
=
. Отсюда коэффициент Джини G=1
–2l=
=
. Очевидно, что при a>1 G>0
и G
®
0
при a®¥
, а при a®1 G
®1.
Пример 2. Равномерное распределение. Пусть распределение доходов равномерно на отрезке [a, b],
т.е. F(w)=0
при w<a, F(w)=(w
-a)/(b
-a)
при a
£
w<b
и F(w)=1
при w
³
b.
Известно, что среднее значение доходов W
в этом случае равно (b+a)/2.
Кривая Лоренца получается из соотношения L(w)=
zF(z) dz=
dz=(w2
-a2
)/(b2
-a2
).
Площадь под кривой Лоренца l=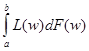
=
+
, а коэффициент Джини G=1
–2l.
Удобно, как и ранее, выразить коэффициент Джини через средние доходы W
и минимальные a.
Так как W=
,
токоэффициент G
=
.
Последнее означает, что равномерное распределение доходов дает G=0
при W=a
и G=1/3
при W®¥.
Пример 3. Двухточечное распределение. Рассмотрим простейший случай, когда люди имеют доходы только двух размеров – минимальные a
и максимальные b.
В этом случае функция распределения F(w)=0,
при w<a, F(w)=p,
при a
£
w<b,
и F(w)=1,
при w
³
b
, а математическое ожидание дохода равно W=pa+(1
‑p) b.
Теперь кривая Лоренца состоит из двух отрезков прямых линий, проходящих через точки (0,0), (p, p
)
и (1,1)
. Площадь треугольника между диагональю квадрата и сторонами, составляющими кривую Лоренца, будет равна 1/2
‑l
=0,5 (p
-p)
, т.е. половине абсолютной величины определителя
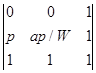
Заключение
Теперь, когда рассмотрены несколько мер расслоения, в том числе дисперсия, отношение квартилей (децилей), энтропия, коэффициенты вариации и Джини можно их сравнивать между собой. Для этого воспользуемся тремя типами распределений среднедушевых доходов, которые уже также были приведены – это распределения Парето, равномерное и двухточечное.
Для такого сравнения, в качестве примера, примем, что минимальный среднедушевой доход a будет считаться единичным. В этом случае математическое ожидание доходов W будет равно k (или ka=W ).
В этом случае функции распределения всех трех типов представимы в виде:
1) Парето – 1
-
,
при х>1 и 0 при х£1;
2) равномерное – 0 при х£1; 
,
при 1<x
£
2k
‑1
и
3) двухточечное – 0 при x
£
1
, p
при 1<x
£
и 1
при x>.
Легко проверить, что математические ожидания всех трех типов распределения равны k (см. задачу 3).
Таблица 1. Меры расслоения
| Распределения | Дисперсия | Энтропия | Коэф. вариации | Коэф. Джини |
| Парето | 
|
|
|
|
| равномерное. |  |
 |
 |
 |
| двухточечное |  |
-p lnp- – ( 1‑p) ln (1 ‑p) |
|
|
Для получения функции Лоренца необходимо получить интеграл L(w)=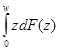
,
который равен для распределения Парето (тип 1):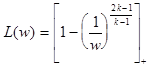
, где [x
]+
=max [0, x
]; для равномерного распределения (тип 2) L(w)=0
при w
£
1, L(w)=
при 1<w
£
2k-L(w)=1
при w>
2k‑1, наконец, для двухточечного распределения (тип 3) имеем координаты кривой (ломаной) Лоренца (w, L(w))
: L(w)=1/k.
при 0<w
£
p
, 
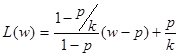при p<w
£
1
, где w
– доля людей, получающая долю доходов L(w).
Таким образом, кривая Лоренца (в данном случае, ломаная линия), состоит из двух отрезков прямых, соединяющих точки (0,0
), (p
, p/k
) и (1,1
), а площадь треугольника с вершинами в этих точках (см. задачу 4) равна 
.
Используемый ранее в главе интеграл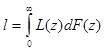 
будет встречаться далее, но в другом смысле и для других целей. Сейчас же обратим
10-09-2015, 16:08