Возникает вполне резонный вопрос: для чего нужно такое довольно громоздкое описание человека, ведь есть достаточно простые и хорошо работающие модели движения населения. Ответ состоит в том, что самые простые модели – это Марковские модели. Теперь, если сделать интенсивности (вероятности) переходов зависимыми от признаков человека на старом исходном месте и новом, куда он прибывает, то станет очевидным, что переходы зависят лишь от сравнения исходного места и места прибытия, т.е. поведение человека в ближайшее время при будущем переходе описывается только его характеристиками в настоящем. А это и есть грубый признак марковости. Действительно, в настоящем человек располагает набором x , который он при решении вопроса о переходе сравнивает с тем, чем он будет располагать в будущем – с набором y .
4. Проверка марковости
Переходы людей наблюдаются статистическими бюро различных стран и доступны для исследователя. Отсюда появляется задача связать это движение с выбором лучшего каждым человеком. Известные модели движения населения (чаще всего это макромодели) обычно предполагают, что разные группы людей связываются потоками переходов. Более того, далее будут приведены зависимости, связывающие межгрупповые потоки людей с условиями в разных группах. Эти условия служат мотивами переходов и называются обычно факторами подвижности. Как макро так и микро модели движения людей, в которых учитываются факторы подвижности называют обычно факторными .
Факторные микромодели наиболее распространены среди исследователей миграции, реже они встречаются, когда говорят о социальной мобильности или межотраслевом движении. Чаще всего, как будет видно при исследовании макромоделей, факторные модели учитывают зависимость будущего статуса человека от его настоящего. Хотя это и упрощает действительную зависимость, но взамен дает возможность рассчитывать будущее в зависимости только от настоящего. Такой вид зависимости математики обычно называют Марковской зависимостью. Далее, когда будет встречаться такое упрощение, всегда будет говориться о марковости, Марковской зависимости или модели.
Несмотря на то, что наиболее часто встречающиеся в литературе факторные модели движения населения почти всегда бывают Марковскими, нигде не встречается доказательство того, что это действительно так, хотя для некоторых моделей (в частности, при делении людей на «оседлых» и «кочевников») известно, что они не могут быть Марковскими. Поскольку Марковские модели обладают рядом свойств, то выполнимость этих свойств необходимо проверять. Но это никогда не делалось. Этот пробел будет заполнен далее.
Решение о переходе принимается или нет, в зависимости от сравнения x и y , т.е. имеется некоторая функция f (x, y ), связывающая силу тяги со старого места x в новое y , а f (x, x ) дает привлекательность состояния y =x такую же, как на старом месте. Наверное перехрды будут в том случае, когда f (x, y )>f (x, x ) , при этом предполагается, что функция f (x, y ) будет связана, скажем, с вероятностью перехода индивида из состояния x в состояниеy . Эта связь очень проста для Марковских моделей с непрерывным временем, так как для них f (x, y ) – это может быть интенсивностью перехода, а для Марковских моделей с дискретным временем и, как правило, достаточно малойединицей времени h f (x, y ) h – вероятность перехода из состояния x в состояниеy . Остается проверить лишь условия, которые необходимы для марковости.
Рассмотрим группы, обозначенные символами i и j , состоящие из мест с эквивалентными условиями жизни и труда: i – группа с условиями, эквивалентными x – любыми исходными условиями x ÎXi , j – группа с конкретными условиями y , куда человек переходит или стремится попасть, или эквивалентными им x j ; множество Xj содержит и условия y . Поскольку функция f (x, y ) принимает при любых x ÎXi и y ÎXj =Yj одни и те же значения, то f (x, y )= l ij . Теперь интенсивности переходов между группами i и j будт функциями от факторов x и y .
Покажем, что факторная модель переходов отдельных людей (микро модель) между условиями x на старом и y на новом местах может быть Марковской. Для моделей с непрерывным временем достаточно проверить, что матрица интенсивностей переходов C = ºcij º обладает двумя свойствами: а) квазинеотрицательностью и б) суммы элементов каждой строки равные 0, т.е. Ce =0 , гдеe =(1,1,…, 1)T .
Положим далее интенсивности переходов l
ij
=f (
x, y
)
из условий x
ÎXi
в y
Î
Yj
. Тогда, обозначив через l
i
(Yj
)
интенсивность переходов в группу j
, которая может состоять не обязательно как ранее из эквивалентных условий, получим l
i
(Yj
)=
, а для интенсивности переходов в любую группу (интенсивности выхода из группы i)
ri
=
. Теперь легко увидеть, что необходимые условия а) и б) выполняются для матрицы C
=
-R+
L
, где L
=ºl
ij
º, а R –
диагональная матрица с диагональными элементами ri
.
Кстати, при фиксированном x
и произвольном множестве Yj
, функция l
i
(Yj
)
будет переходной функцией Марковского процесса. Таким образом, факторная модель движения населения будет Марковским случайным процессом с переходными вероятностями l
ij
=f (
x, y
).
Для Марковских моделей с дискретным временем аналогично. Действительно эти модели могут быть Марковскими лишь тогда, когда вероятности перехода pij из одного состояния (скажем, i) в другое (j), во-первых, неотрицательны, а, во-вторых, сумма pij по всем j для любого i равна 1. Если допустить, что pij =f (x, y ) h, где условия x присущи индивиду из групп i, аy – у словия, на которые он переходит в группу j за время h , то оказывается (см. например [Староверов, 1979]), что pij могут быть только постоянными величинам, т.е. не могут меняться для разных групп i и j. Это значит, что модели, описанные, например, в [Бартоломью] не могут быть факторными, т.е. вероятности переходов не зависят от разных условий индивидов в группах i и j (скажем, проживающих в разных районах).
Однако, когда матрица P=R
-R+I
,
где R
диагональная матрица, состоящая из элементов ri
h,
равных сумме f (
x, y
) h
по любымy,
x
– какие-либо из эквивалентных условий в группе i
, а y
– любые условия после перехода в группу j
эквивалентных условий y
,
то модель может быть Марковской. Действительно, для любых функций f (
x, y
)>0
и ri
=
, если вероятности pij
=ri
h
при i
¹
j
и pii
=1
‑ri
h+ri
h
, где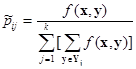 
вероятность перехода из группы i
с эквивалентными условиямиx
Î
Xi
в группу j
с эквивалентными условиями y
Î
Yj
после выхода из группы i,
то вероятности pij
уже неотрицательны и в сумме по j
равны 1. Доказательство очевидно (см., например, [Староверов, 1979])
Итак, показано, что модель движения населения может зависеть от факторов подвижности так, что ее параметры (интенсивности перехода для случая непрерывного времени, вероятности перехода – для дискретного) представляют собой функции лишь от факторов в группе выхода (i ) и группе попадания (j). Такая возможность, правда, дает лишь косвенное подтверждение марковости, так как сама марковость следует из трех гипотез, одна из которых говорит о том, что вероятности перехода l ij h за малый интервал времени h зависят только от групп i и j, т.е., как сейчас стало ясно, от факторов подвижности только в этих двух группах.
Подчеркнем еще раз, что рассматриваются люди, которые перемещаются по состояниям x
(т.е. из состояния x
Î
Xi
в y
Î
Xj
) и лишь множества Xi
и Xj
относят человека к той или иной группе (с эквивалентными или произвольными условиями). Если же 
– все условия, предоставляемые людям, то принадлежность к группе определяется сторонним наблюдателем, которому удобнее рассматривать группы людей и движение между ними, а не переходы отдельного человека.
5. Основные свойства
Функции f ( x, y ) в первую очередь показывают, как отдельный человек сравнивает одни условия с другими, насколько одни условия (y) привлекательнее других (x ), так как без улучшения условий своей жизни и труда. Более того, чем больше улучшаются условия при переходе, тем больше люди будут стремиться их обретать и тем чаще будут происходить перемещения людей. Таково основное предположение всех факторных моделей. Другими словами, люди по собственному желанию в заведомо худшие условия не пойдут, их можно загнать туда толь насильно или обманом – уж таковы предпочтения человека при переходе с одного места на другое. Поэтому будем называть интенсивности переходов до специально оговоренного случая еще функциями привлекательности, тяги или предпочтения , не различая эти термины, как и было отмечено ранее.
Функции f ( x, y ), показывающие зависимость интенсивности перемещения от уровней предпочтения, степени привлекательности или силы тяги, были известны давно, как и их общие свойства. Например, при улучшении своего положения (увеличении компонент набора x ), индивид уменьшает свое желание к переходам на другие фиксированные условия (y ). Наоборот, при фиксированном набореx , улучшение условийy , предлагаемых человеку в другом месте, желательность перехода, поэтому и его интенсивность, будет возрастать.
Для экологических факторов, таких как загрязненность, радиация и т.д., если есть потребность представлять их как заработки, т.е. при увеличении значений факторов предпочтение также растет, их следует представлять в виде либо обратных величин, либо результата вычитания показателя из некоторого условного уровня, например, предельно допустимой нормы. Далее будут указаны другие возможности.
Будем для простоты считать все факторы непрерывно меняющимися, а функции f (
x, y
)
– гладкими, тогда в математическом виде интенсивности переходов f (
x, y
)
обладают следующими свойствами: 
, a 
(см., [4]). Поскольку x
– вектор, то – 
будет вектором 
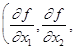
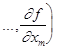, а неравенства <0 или 
>0 означает положительность (для 
) всех компонент, или их отрицательность (для ).
6. Примеры. Эти общие свойства справедливы для всех частных случаев, которые были использованы для моделирования миграции.
Пример 1. (аддитивная или линейная интенсивность переходов). Наиболее простой представляется такая зависимость функции интенсивности f (
x, y
)
когда она линейна как по x
так и по y
.
Наиболее общий вид такой функции f (
x, y
)=a
-
x
+
, где a
– скаляр (число), аb
i
x
и y
– векторы-столбцы. Однако, чаще всего используется частный случай, когдаb
1
=
b
2
=
b
.
Это связано с тем, что предельная эффективность одного и того же фактора при одних и тех же условиях одинакова по абсолютной величине и отличается только знаком (этот вопрос подробнее обсуждается далее). Таким образом, чистая линейная или аддитивная интенсивность переходов имеет вид:
f ( x , y )=a+ b T ( y -x ).
Пример 2. (Мультипликативная интенсивность переходов). Другой частный вид интенсивности переходов состоит в том, что каждый фактор подвижности как бы умножает действия всех остальных, т.е. увеличившись в несколько раз, повышает предпочтения всех остальных в то же самое количество раз. Частный случай таков:
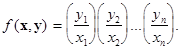
В более общем виде, который чаще всего использовался в практике моделирования, интенсивность переходов обычно записывается следующим образом:
f (
y
, x
)=
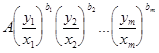
Замечание . Видно, что последняя функция из примера 2 связана с функцией из примера 1 тем, что после логарифмирования и измерения факторов и предпочтений в логарифмической шкале они совпадают. Действительно,
lnf ( x , y )= lnA+b1 ( lny1 -lnx1 ) +b2 ( lny2 -lnx2 )+… +bm ( lnym -lnxm ),
т.е. логарифм мультипликативной функции предпочтения совпадает с линейной функцией предпочтения, если вместо факторов подвижности подставит их логарифмы.
7. Предельная эффективность факторов
Интенсивности переходов f (x, y) (вероятности при дискретном времени) обычно связаны (пропорциональны) функции предпочтения. Поэтому при всех фиксированных условиях (наборах факторов x и y ) и интенсивности переходов и предпочтения постоянны. Но возникает вопрос, что будет происходить с этими функциями, а, следовательно, с переходами людей при малых изменениях какого-либо одного фактора подвижности, скажем, xs , когда все остальные факторы не изменяются, т.е. при прочих равных условиях.
Математически малые изменения df
(x, y)=
dxs
. При изменении ys
изменение интенсивностей переходов df (
x, y
)
=
dys
, но теперь можно учесть, что <0, а >0. Отсюда следует, что при увеличении xs
, например, реальной оплаты труда, на величину dxs
>0 интенсивность переходов уменьшается (dxs
>0, а <0), а при ее уменьшении на старом месте – увеличивается (dxs
<0, <0, т.е. dxs
>0). Аналогично, но с обратным знаком для ys
.
Теперь ясно, что кроме знака изменения интенсивности переходов известно и во сколько раз ( или ) отличается изменение функции при малом изменении аргумента (dxs
, dys
), что дает основание называть соответствующую производную или предельной эффективностью фактора s,
т.е. xs
и ys
соответственно.
Пример 3. Найдем эффективность действия фактора xs
(и ys
) для интенсивности переходов линейного вида, зависящей от трех факторов (s
=1,2,3); f (
x, y
)
=a+b
T
(y
-x
)
= =a+b1
(y1
-x1
)+b2
(y2
-x2
)+b3
(y3
-x3
).
В этом случае =-bs
, а =bs
, т.е. для любого из трех факторов предельная эффективность его не зависит от значений остальных т.е. факторы увеличивают или уменьшают интенсивности независимо от значений остальных. Последнее обстоятельство сильно упрощает вычисления.
Пример 4. Найдем эластичность интенсивности от фактора xs
(ys
)
для функции из примера 2. Для этого проще всего воспользоваться уже сделанным логарифмическим преобразованием, из которого следует, что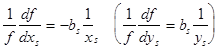 
(см. также задачу 1). Последние соотношения говорят о том, что эластичности интенсивности переходов от факторов (т.е. отношение 
к 
и 
) постоянны по абсолютной величине для любого s
, но для разных s
они, вообще говоря, разные.
Из примеров 3 и 4 следует, что интенсивность переходов для примера 1 можно было бы назвать интенсивностью переходов с постоянными эффективностями факторов, а интенсивность переходов из примера 2 – интенсивностью переходов с постоянными эластичностями. Однако можно пользоваться и тем и другим названием. Гораздо важнее для дальнейшего то, что отношения а) эффективностей одноименных факторов исходных и финальных условий для интенсивности переходов с постоянной эффективностью и б) отношение эластичностей от тех же самых факторов интенсивностей переходов с постоянными эластичностями равны друг другу, так как они равны -1.
Задачи
1. Убедитесь, что равенства 
справедливы и без логарифми-ческого преобразования функции полезности из примера 2.
2. Пусть интенсивность перехода f ( x, y ) =a +b T (y -x ), где a=0,5, аb T =(2,3,4), и индивид, имеющий x=(0,4; 0,3; 0,2), рассматривает возможные переходы в другие группы на места y 1 =(0,3; 0,2; 0,3), y 2 =(0,2; 0,4; 0,1) и y 3 =(0,41; 0,29; 0,25) На какие места (1, 2, или 3) человек будет претендовать? Сколько их всего?
3. Сколько привлекательных мест для человека из задачи 2, если а) на каждом месте y i (i=1,2,3) работают по 10 человек; б) если набором y 1 обладают 50, y 2 – 40, а y 3 – 10 человек? Сколько их всего?
4. Есть группы, в которые можно перейти человеку из задачи 2. Исходная группа соответствует задаче 2, а другие предоставляет те же y 1 , y 2 , y 3 , что в задаче 3б, но добавлеена еще группа с y 4 = =(o, 35; 0,2; 0,31 ). Обсудите вопрос какая из групп предпочтительнее, если на местах с y 1 находятся 10 человек, а с y 2 , – 30, с y 3 – 20, а с y 4 – 15 человек.
5. Пусть интенсивность перехода соответствует задаче 2 и рассматриваются интенсивности перехода в группу j с состояниями y 1 , y 2 , y 3 из задачи 3 из группы i с состояниями x из задачи 2. Обсудите вопрос о том, что интенсивности перехода в группу j из группы i а) зависят лишь от x ; б) зависят от средних значений y 1 , y 2 , y 3 . Какую функцию от a+ b T ( y -x ) можно взять в качестве интенсивности перехода?
Литература
1. Бартоломью Д. Стохастические модели социальных процессов. Изд. «Финансы и статистика», Москва, 1985 г.
2. Бедность: альтернативные подходы к определению и измерению. Cornegie Endowment for International Peace. М. 1998 г.
3. Белкина Т.А., Лёвочкина М.С. Исследование модели оптимального управления негосударственным пенсионным фондом. В сборнике «Математические
10-09-2015, 15:18