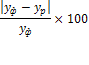Рабочая формула метода экспоненциального сглаживания:
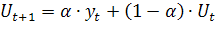 (2)
(2)
где t
– период, предшествующий прогнозному; t
+1
– прогнозный период; ![]() - прогнозируемый показатель;
- прогнозируемый показатель; ![]() - параметр сглаживания;
- параметр сглаживания; ![]() -фактическое значение исследуемого показателя за период, предшествующий прогнозному;
-фактическое значение исследуемого показателя за период, предшествующий прогнозному; ![]() экспоненциально взвешенная средняя для периода, предшествующего прогнозному.
экспоненциально взвешенная средняя для периода, предшествующего прогнозному.
При прогнозировании данным методом возникает два затруднения:
1) выбор значения параметра сглаживания α ;
2) определение начального значения U о .
От величины α будет зависеть, как быстро снижается вес влияния предшествующих наблюдений. Чем больше α , тем меньше сказывается влияние предшествующих лет. Если значение α близко к единице, то это приводит к учету при прогнозе в основном влияния лишь последних наблюдений; если близко к нулю, то веса, по которым взвешиваются уровни временного ряда, убывают медленно, т.е. при прогнозе учитываются все (или почти все) прошлые наблюдения. Таким образом, если есть уверенность, что начальные условия, на основании которых разрабатывается прогноз, достоверны, следует использовать небольшую величину параметра сглаживания (α→0). Когда параметр сглаживания мал, то исследуемая функция ведет себя как средняя из большого числа прошлых уровней. Если нет достаточной уверенности в начальных условиях прогнозирования, то следует использовать большую величину α, что приведет к учету при прогнозе в основном влияния последних наблюдений.
Точного метода для выбора оптимальной величины параметра сглаживания α нет. В отдельных случаях автор данного метода профессор Браун предлагал определять величину α, исходя из длины интервала сглаживания. При этом α вычисляется по формуле:
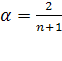 (3)
(3)
где n – число наблюдений, входящих в интервал сглаживания.
Задача выбора U о (экспоненциально взвешенного среднего начального) решается следующими путями:
1) если есть данные о развитии явления в прошлом, то можно воспользоваться средней арифметической, и U о равен этой средней арифметической;
2) если таких сведений нет, то в качестве U о используют исходное первое значение базы прогноза Y 1 .
Также можно воспользоваться экспертными оценками.
Используем метод экспоненциального сглаживания для составления прогнозных значений. Величина параметра сглаживания для показателя численности населения составит: 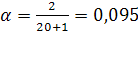 , для показателей «число родившихся» и «число умерших», «число прибывших» и «число выбывших»:
, для показателей «число родившихся» и «число умерших», «число прибывших» и «число выбывших»: 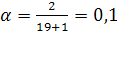 . Значения близки к нулю, следовательно, веса, по которым взвешиваются уровни временного ряда, убывают медленно, т.е. при прогнозе учитываются все (или почти все) прошлые наблюдения.
. Значения близки к нулю, следовательно, веса, по которым взвешиваются уровни временного ряда, убывают медленно, т.е. при прогнозе учитываются все (или почти все) прошлые наблюдения.
Определяем начальное значение U о для показателя численности населения двумя способами:
1 Способ (средняя арифметическая): 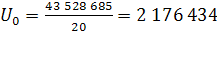
2 Способ (первое значение базы прогноза):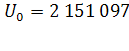
Рассчитываем экспоненциально взвешенную среднюю для каждого года, используя формулу 2, занесем результаты в таблицу.
Таблица 4
Расчет прогнозного значения численности населения Оренбургской области методом экпоненциального сглаживания.
| года | Численность постоянного населения на 1 января, человек | Экспоненциально взвешенная средняя Ut | Расчет средней относительной ошибки
|
|||||
| I способ | II способ | I способ | II способ | |||||
| 1 | 1990 | 2 151 097 | 2176434 | 2 151 097 | 1,18 | 0,00 | ||
| 2 | 1991 | 2 159 743 | 2174021 | 2 151 097 | 0,66 | 0,40 | ||
| 3 | 1992 | 2 168 257 | 2172661 | 2 151 920 | 0,20 | 0,75 | ||
| … | ||||||||
| 19 | 2008 | 2 119 003 | 2175920 | 2 171 738 | 2,69 | 2,49 | ||
| 20 | 2009 | 2 111 531 | 2170499 | 2 166 716 | 2,79 | 2,61 | ||
| прогноз | 2010 | 2 164 883 | 2 161 460 | |||||
| итого | 43 528 685 | 27,20 | 29,84 | |||||
| Средняя относительная ошибка ɛ | 1,36 | 1,49 | ||||||
| Средняя абсолютная ошибка Δ |
-6064 | 5441 | ||||||
| Средняя квадратическая ошибка |
33749 | 36868 | ||||||
Величина средней относительной ошибки при расчете 2-м способом выше, но оба значения свидетельствуют о высокой точности прогноза.
Данные о прогнозных значениях показателей других демографических показателей, представим в таблице (расчет полученных параметров в Приложении 2).
Таблица 5
Прогнозные значения абсолютных показателей родившихся и умерших, прибывших и выбывших в Оренбургской области, полученные методом экспоненциального сглаживания.
| Абсолютный показатель, человек | 2006 | 2007 | 2008 | Прогноз на 2009 | Δ |
ε | ||||
| I способ определения экспоненциально взвешенного среднего начального | ||||||||||
| Родившиеся | 23 335 | 25 776 | 26 947 | 23 915 | -135 | 3 275 | 9,94 | |||
| Умершие | 31 583 | 31 000 | 30 904 | 30 754 | 64 | 2 571 | 8,14 | |||
| II способ определения экспоненциально взвешенного среднего начального | ||||||||||
| Родившиеся | 23 335 | 25 776 | 26 947 | 25 150 | -4296 | 5 386 | 20,14 | |||
| Умершие | 31 583 | 31 000 | 30 904 | 29 557 | 1 241 | 2 965 | 14,91 | |||
| I способ определения экспоненциально взвешенного среднего начального | ||||||||||
| Прибывшие | 31 949 | 25 570 | 28 053 | 37 366 | -3539 | 15857 | 35,27 | |||
| Выбывшие | 33 225 | 29 085 | 25 603 | 36311 | -2070 | 8458 | 20,04 | |||
| II способ определения экспоненциально взвешенного среднего начального | ||||||||||
| Прибывшие | 31 949 | 25 570 | 28 053 | 41 292 | -16856 | 19228 | 49,84 | |||
| Выбывшие | 33 225 | 29 085 | 25 603 | 38 162 | -8348 | 9757 | 24,83 | |||
Так же как и с показателем численности населения, величина средней относительной ошибки при расчете 2-м способом выше, что свидетельствует о нецелесообразности применения первого значения базы прогноза в качестве экспоненциально взвешенной U о . В целом точность прогноза для показателей естественного движения населения находится в границах высокой точности, для показателей миграционного движения точность прогноза удовлетворительная.
2.3 Нахождение прогнозных значений методом наименьших квадратов
демографический прогноз население численность
Сущность метода наименьших квадратов состоит в минимизации суммы квадратических отклонений между наблюдаемыми и расчетными величинами. Расчетные величины находятся по подобранному уравнению – уравнению регрессии.
Чем меньше расстояние между фактическими значениями и расчетными, тем более точен прогноз, построенный на основе уравнения регрессии. Теоретический анализ сущности изучаемого явления, изменение которого отображается временным рядом, служит основой для выбора кривой. Иногда принимаются во внимание соображения о характере роста уровней ряда. Для нахождения прогнозных значений численности населения часто предполагается, что рост идет в геометрической прогрессии, и тогда сглаживание производится по показательной функции.
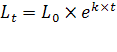 (4)
(4)
где ![]() - численность населения в прогнозный период;
- численность населения в прогнозный период; ![]() - численность населения в период, предшествующий прогнозному; е
- основные натурального логарифма; k
- общий коэффициент прироста населения, выраженный в долях единиц, рассчитанный по формуле:
- численность населения в период, предшествующий прогнозному; е
- основные натурального логарифма; k
- общий коэффициент прироста населения, выраженный в долях единиц, рассчитанный по формуле: 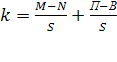 (5)
(5)
где M - число родившихся за период; N – число умерших за период; П - число прибывших за период; В – число выбывших за период; S – средняя численность населения за период; t- период, на который разрабатывается прогноз.
Согласно имеющимся данным, численность населения Оренбургской области на 1 января 2008 года составила 2 119 003 чел., на 1 января 2009 – 2 111 531 чел., за 2008 год родилось 26 947 чел., умерло 30 904 чел., 25 570 чел. прибыло и 29 085 чел. выбыло. Рассчитаем численность населения в 2010-2012 гг. при условии, что коэффициент общего прироста населения (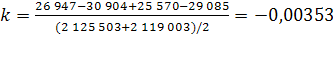 ) останется неизменным на всем протяжении прогнозных лет:
) останется неизменным на всем протяжении прогнозных лет:
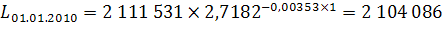 чел.
чел.
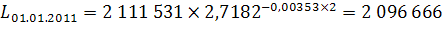 чел.
чел.
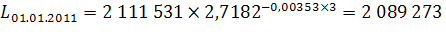 чел.
чел.
Сглаживание временных рядов методом наименьших квадратов служит для отражения закономерности развития изучаемого явления. В аналитическом выражении тренда время рассматривается как независимая переменная, а уровни ряда выступают как функция этой независимой переменной. Ясно, что развитие явления зависит не от того, сколько лет прошло с отправного момента, а от того, какие факторы влияли на его развитие, в каком направлении и с какой интенсивностью. Развитие явления во времени выступает как результат действия этих факторов.
Правильно установить тип кривой, тип аналитической зависимости от времени – одна из самых трудных задач предпрогнозного анализа.
Подбор вида функции, описывающей тренд, параметры которой определяются методом наименьших квадратов, производится в большинстве случаев эмпирически, путем построения ряда функций и сравнения их между собой по величине среднеквадратической ошибки, вычисляемой по формуле:
![]() (6)
(6)
где ![]() – фактические значения ряда динамики;
– фактические значения ряда динамики;![]() – расчетные (сглаженные) значения ряда динамики; n
– число уровней временного ряда; р
– число параметров, определяемых в формулах, описывающих тренд.
– расчетные (сглаженные) значения ряда динамики; n
– число уровней временного ряда; р
– число параметров, определяемых в формулах, описывающих тренд.
С помощью программы Excel проверим предположение о том, что изменение численности населения в Оренбургской области, хорошо апроксимируется экспоненциальной линией тренда.

Рис. 1. Динамика численности населения в Оренбургской области с экспоненциальной линией тренда.
Видно, что разница между фактическими и сглаженными значениями данного ряда очень велика. Невысокий коэффициент достоверности аппроксимации также подтверждает, что использовать данный тип тренда нецелесообразно.
Наибольшее приближение к фактическим уровням данного динамического ряда дает функция полинома второй степени.
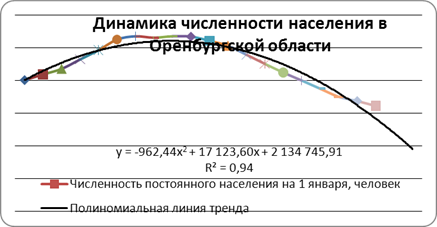
Рис. 2. Динамика численности населения в Оренбургской области с полиномиальной линией тренда.
При использовании уравнения полинома третьей степени, коэффициент аппроксимации увеличивается до 0,97, но при этом усложняется и сама модель, что может отрицательно сказаться на ее прогностических возможностях.
Уравнение регрессии примет вид:
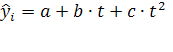 (7)
(7)
![]() - выровненные, т.е. лишенные колебаний, уровни тренда для лет с номером i
; а -
это средний (выровненный) уровень тренда на момент или период, принятый за начало отсчета времени, т.е. t
=
0;
b
-
это средний за весь период среднегодовой прирост, который изменяется равномерно со средним ускорением, равным 2с; c
-
константа, главный параметр параболы II порядка.
- выровненные, т.е. лишенные колебаний, уровни тренда для лет с номером i
; а -
это средний (выровненный) уровень тренда на момент или период, принятый за начало отсчета времени, т.е. t
=
0;
b
-
это средний за весь период среднегодовой прирост, который изменяется равномерно со средним ускорением, равным 2с; c
-
константа, главный параметр параболы II порядка.
Параметры a , b и c оцениваются методом наименьших квадратов и отвечают принципу максимального правдоподобия: сумма квадратов отклонений фактических уровней от тренда (от выровненных по уравнению тренда уровней) должна быть минимальной для данного типа уравнения.
На диаграмме уравнение тренда имеет вид: 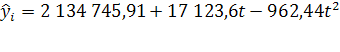 ,
где
,
где ![]() =0 в 1990г.
=0 в 1990г.
При этом нумерация периодов начинается с t
=1. Однако рациональнее начало отсчета времени перенести в середину ряда, т.е. при нечетном п -
на период (момент) с номером (п +
1 )/2, а при четном числе уровней ряда - на середину между периодом с номером n
/2
и (n/2)+1. Расчет параметров тренда при переносе отсчета времени на середину ряда приведен в приложении 3. Тогда уравнение тренда принимает вид: 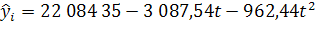 , где
, где ![]() =0,5 в 2000г.
=0,5 в 2000г.
За период 1990-2009г показатель численности населения в Оренбургской области убывал в номинальной оценке ускоренно, со средним ускорением 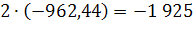 человек за год; средняя убыль населения за весь период составила 3 087 человек; средний уровень численности населения на середину периода был равен 22 084 35 чел.
человек за год; средняя убыль населения за весь период составила 3 087 человек; средний уровень численности населения на середину периода был равен 22 084 35 чел.
Для оценки надежности тренда необходимо оценить надежность его главного параметра – ускорения. Средняя ошибка репрезентативности выборочной оценки параметра с вычисляется по формуле:
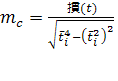 (8)
(8)
Где S ( t ) – оценка генерального показателя колеблемости, учитывающая потерю степеней свободы и определяемая по формуле 6.
Используя данные приложения 3, найдем искомые величины:
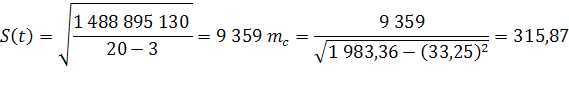
Отношение параметра с
(половина ускорения) к его средней ошибке - это t-критерий Стьюдента: 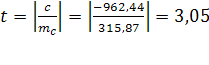
Табличное значение критерия Стъюдента 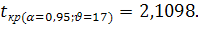 Фактическая величина критерия больше табличного, следовательно, вероятность нулевой гипотезы (о равенстве параметра с
нулю) чрезвычайно мала. Достоверно известно, что тренд существовал, и что численность населения Оренбургской области снижалась не случайно.
Фактическая величина критерия больше табличного, следовательно, вероятность нулевой гипотезы (о равенстве параметра с
нулю) чрезвычайно мала. Достоверно известно, что тренд существовал, и что численность населения Оренбургской области снижалась не случайно.
Прогноз по этой модели заключается в подстановке в уравнение тренда номера периода, который прогнозируется. Для 2010 года период времени t = 10,5, прогнозное значение составит:
![]() 2010
=
2010
=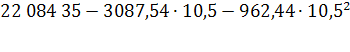 =2 069 907 чел.
=2 069 907 чел.
Полученное прогнозное значение является точечным и не учитывает колеблемость уровней показателя.
При прогнозе с учетом случайной колеблемости учитывается как вызванная колеблемостью ошибка репрезентативности выборочной оценки тренда, так и колебания уровней в отдельные периоды (моменты) относительно тренда.
Общая формула средней ошибки прогноза положения параболического тренда на период с номером ![]() от середины базы расчета тренда имеет вид:
от середины базы расчета тренда имеет вид:
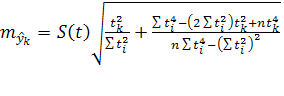 (9)
(9)
Средняя ошибка тренда на 2010 год равна:
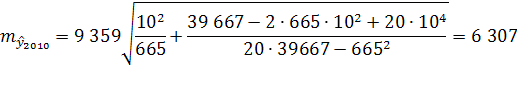
Вероятность того, что фактическая ошибка не превысит одного среднего квадратического отклонения, т.е. m равна при нормальном распределении 0,68. Чтобы получить доверительный интервал прогноза линии тренда с большей вероятностью, например с вероятностью 0,95,среднюю ошибку нужно умножить на величину t-критерия Стъюдента для вероятности 0,95 и n - p степеней свободы.
Получаем вероятную ошибку:
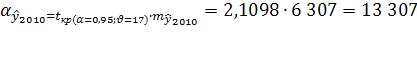
с вероятностью 95% можно утверждать, что тренд численности населения в Оренбургской области в 2010 году проходит в границах 2 069 907±13 307 или от 2 056 600 до 2 083 214 человек.
Определив ошибку репрезентативности выборочной оценки тренда, и колебания уровней в отдельные периоды (моменты) относительно тренда, получаем единую формулу средней ошибки прогноза конкретного отдельного уровня:
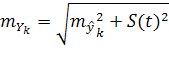 (10)
(10)
Для искомого прогнозного значения: 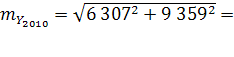 11 286
11 286 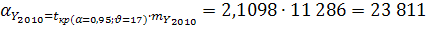 .
.
Таким образом, для прогнозного значения показателя численности населения на 1 января 2010 года определены границы доверительного интервала 2 046 096 – 2 093 718 человек.
Аналогично рассчитываем прогнозные значения на 2011-2012 годы:
![]() 2011
=2 045 646 чел.
2011
=2 045 646 чел. 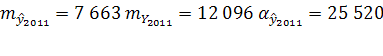
Доверительный интервал: (2 020 126; 2 071 166).
![]() 2012
=2 019 459 чел.
2012
=2 019 459 чел. 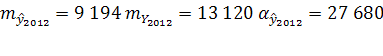
Доверительный интервал: (1 991 780; 2 047 138)
Средняя относительная ошибка 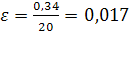 , что свидетельствует о высокой точности прогноза.
, что свидетельствует о высокой точности прогноза.
Расчет прогнозных значений для других показателей приведен в приложении 3, сведем полученные результаты в общую таблицу:
Таблица 5
Прогнозные значения абсолютных показателей родившихся и умерших, прибывших и выбывших в Оренбургской области, полученные методом наименьших квадратов.
| Абсолютный показатель, человек | 2006 | 2007 | 2008 | Прогноз на 2009 | Прогноз на 2010 | Прогноз на 2011 | Δ |
ε | |
| Родившиеся | 23335 | 25776 | 26947 | 29 253 | 31 220 | 33 395 | 0 | 1135 | 4,13 |
| Умершие | 31 583 | 31 000 | 30 904 | 30 190 | 29 392 | 28 470 | 0 | 1420 | 3,69 |
| Абсолютный показатель, человек | 2007 | 2008 | 2009 | Прогноз на 2010 | Прогноз на 2011 | Прогноз на 2012 | Δ |
ε | |
| Прибывшие | 31 949 | 25 570 | 28 053 | 29 586 | 31 144 | 33 202 | 0,11 | 3499 | 7,68 |
| Выбывшие | 33 225 | 29 085 | 25 603 | 24 352 | 22 589 | 20 826 | 0 | 2437 | 5,17 |
Величины относительной ошибки свидетельствуют о высокой точности прогноза. По имеющимся данным видно, что при наметившихся тенденциях естественный прирост населения в прогнозируемые годы увеличится (увеличение рождаемости и снижение смертности), как и миграционный прирост.
Для сравнения полученных результатов составим сводную таблицу по всем применяемым методам:
| Численность постоянного населения на 1 января, человек | |||||||||
| МСС | МЭС | МНК | |||||||
| 2007 | 2 125 503 | 2 125 503 | 2 125 503 | ||||||
| 2008 | 2 119 003 | 2 119 003 | 2 119 003 | ||||||
| 2009 | 2 111 531 | 2 111 531 | 2 111 531 | ||||||
| прогноз | |||||||||
| 2010 | 2 116 188 | 2 164 883 | 2 069 907 | ||||||
| 2011 | 2 117 127 | 2 045 646 | |||||||
| 2012 | 2 115 261 | 2 019 459 | |||||||
| Ср. абсолют. оценка | 299 | -6064 | 0,38 | ||||||
| Ср. квадрат. оценка | 1 478 | 33749 | 8628 | ||||||
| Ср. относит. ошибка | 0,05 | 1,36 | 0,017 | ||||||
| Число родившихся, чел. | Число умерших, чел. | ||||||||
| МСС | МЭС | МНК | МСС | МЭС | МНК | ||||
| 2 006 | 23335 | 23335 | 23335 | 31 583 | 31 583 | 31 583 | |||
| 2 007 | 25776 | 25776 | 25776 | 31 000 | 31 000 | 31 000 | |||
| 2 008 | 26947 | 26947 | 26947 | 30 904 | 30 904 | 30 904 | |||
| прогноз | |||||||||
| 2 009 | 25 743 | 23 915 | 29 253 | 31 130 | 30 754 | 30 190 | |||
| 2 010 | 25 754 | 31 220 | 31 087 | 29 392 | |||||
| 2 011 | 26 125 | 33 395 | 31 026 | 28 470 | |||||
| Ср. абсолют. оценка | -85 | -135 | 0 | 32 | 64 | 0 | |||
| Ср. квадрат. оценка | 594 | 3 275 | 1135 | 795 | 2 571 | 1420 | |||
| Ср. относит. ошибка | 2 | 9,94 | 4,13 | 2,02 | 8,14 | 3,69 | |||
| Число прибывших, человек | Число выбывших, человек | ||||||||
| МСС | МЭС | МНК | МСС | МЭС | МНК | ||||
| 2007 | 31 949 | 31 949 | 31 949 | 33 225 | 33 225 | 33 225 | |||
| 2008 | 25 570 | 25 570 | 25 570 | 29 085 | 29 085 | 29 085 | |||
| 2009 | 28 053 | 28 053 | 28 053 | 25 603 | 25 603 | 25 603 | |||
| прогноз | |||||||||
| 2010 | 29 352 | 37 366 | 29 586 | 28 144 | 36311 | 24 352 | |||
| 2011 | 28 091 | 31 144 | 28 457 | 22 589 | |||||
| 2012 | 28 078 | 33 202 | 27 506 | 20 826 | |||||
| Ср. абсолют. оценка | 11 | -3539 | 0,11 | 32 | -2070 | 0 | |||
| Ср. квадрат. оценка | 2 177 | 15857 | 3499 | 1 161 | 8458 | 2437 | |||
| Ср. относит. ошибка | 5 | 35,27 | 7,68 | 2 | 20,04 | 5,17 | |||
Как видно из таблицы, значения средней квадратической оценки средней относительной ошибки у показателей минимальны для метода скользящей средней, и в целом данный метод дает хорошие результаты при прогнозировании демографических процессов. Кроме того, метод прост в использовании, что открывает широкие возможности для его применения. Метод наименьших квадратов более сложен в работе, но позволяет получить также достоверные результаты при условии подбора вида линии тренда, хорошо аппроксимирующей исходный динамический ряд.
Применение метода экспоненциального сглаживания целесообразно только при условии использования среднего уровня ряда в качестве начального значения экспоненциальной взвешенной. Но и в этом случае, полученные результаты являются самыми ненадежными по сравнению с прогнозированием другими методами.
Следует отметить, что прогнозирование методами экстраполяции основывается на использовании простого методологического аппарата и часто используется для получения будущих оценок социально-экономических процессов. Оправдано их использование и в частности при построении демографических прогнозов, поскольку процессы естественного и миграционного движения достаточно инерционны и не подвержены резким скачкам в уровнях.
Заключение
В соответствии с поставленными задачами в данной работе были исследованы 4 группы методов, используемых при прогнозировании демографических процессов:
1) методы экстраполяции;
2) экономико-математические методы, позволяющие разработать многофакторные динамические модели;
3) методы передвижки возрастов и когорт;
4) методы экспертных оценок.
Опираясь на имеющиеся в распоряжении данные, для практической части работы, была выбрана первая группа методов.
10-09-2015, 16:25