Выборочный метод

п — объем выборки.

Таким образом, величина

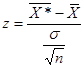
распределена по стандартному нормальному закону (с математическим ожиданием M (z ) = 0и средним квадратическим отклонением σ( z ) = 1).

Задавшись доверительной вероятностью Р = 1 — α, определяем из равенства 2Ф(z) = 1 — α соответствующее значение z_a (используем при этом таблицу интегральной функции Лапласа). Тогда с вероятностью Р = 1 — α выполняется неравенство:

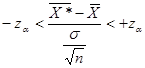(1.9.22)

которое эквивалентно неравенству:

(1.9.23)

Величина называется предельной ошибкой выборки.

Таким образом, мы имеем доверительный интервал для генеральной средней:

( ; )

Наоборот, если задана предельная ошибка ε , а требуется определить вероятность Р, то схема решения задачи следующая:

ε→z=→Ф(z )→P =2Ф(z ) (1.9.24)

Наконец, определение объема выборки п по данным Р и ε производится по следующей схеме:

P =2Ф(z ) →z →n = (1.9.25)

Пример 1.9.4. Взвешивание 50 случайно отобранных коробок печенья дало =1200г. Определить с вероятностью Р = 0,95 доверительные границы для среднего веса коробки печенья в генеральной совокупности, если есть основания полагать, что генеральная дисперсия σ² = 11664.

Решение:

Дано: n =50; = 1200; σ² =11664 (= 108); Р = 0,95.

Из равенства Р = 2Ф(z )=0,95 по таблице значений интегральной функции Лапласа находим z=1,96, откуда:

ε=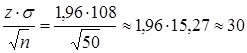(г)

Таким образом, получаем доверительный интервал:

1200 — 30 < < 1200 + 30.

Пример 1.9.5 Определить, с какой доверительной вероятностью можно утверждать, что при данном объеме выборки (50 коробок) ошибка выборки не превысит 20 г.

Решение:

По величине ε=20 вычисляем , откуда по таблице Ф(z ): Р = 2Ф(1,31)≈0,81

Пример 1.9.6. Определить необходимый объем выборки n , который с вероятностью 0,99 гарантировал бы ошибку выборки не более чем ε = 20г.

Решение:

Из Р = 2Ф(z ) =0,99 находим z = 2,58, откуда:

коробок

Предположение о том, что генеральная дисперсия σ² известна при неизвестной генеральной средней, на практике выполняется весьма редко. Чаще всего мы имеем лишь выборочные данные и можем дать лишь выборочную оценку s ² неизвестной дисперсии σ² .

Статистика

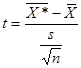(1.9.26)

подчиняется закону распределения Стьюдента с v = n —1 степенями свободы. Однако при больших значениях параметра v (v ≥ 30) распределение Стьюдента практически совпадает с нормальным. Поэтому в случае больших выборок схема решения задач остается прежней, даже если вместо 'Неизве стного генерального среднего квадратического отклонения а используется его выборочная оценка s .

3.5.2. Малая выборка

Если генеральная совокупность подчинена нормальному закону распределения (что на практике имеет место очень часто), то выборочная средняя как средняя арифметическая п нормально распределенных случайных величин также имеет нормальный закон распределения. Таким образом, величина 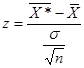распределена по стандартному нормальному закону, и схема решения задач при известном генеральном среднем квадратическом отклонении σ остается прежней.

Если же генеральное среднее квадратическое отклонение σ неизвестно и приходится пользоваться его выборочной оценкой s , то используется статистика t (1.9.26), которая, как мы уже отмечали, подчинена закону распределения Стьюдента с v = n —1 степенями свободы. При v < 30 имеются значительные различия между распределением Стьюдента и нормальным распределением (тем более значительные, чем меньше v ). Используя функцию распределения Стьюдента, мы можем записать равенство, аналогичное формуле Лапласа:

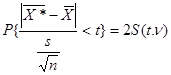(1.9.27)

где S ( t , v ) — функция Стьюдента, значения которой для различных значений t и v подробно рассчитаны и представлены в специальных таблицах.

Выражение ( 1.9.27) эквивалентно выражению:

(1.9.28)

где

Решение задач с помощью этого равенства аналогично решению задач с использованием формулы Лапласа. Лишь определение п несколько усложняется из-за того, что оно входит также в параметр v = n —1.

Поэтому можно воспользоваться схемой последовательных приближений. Вначале производят оценку (s ² ) генеральной дисперсии. Затем находят п₁ по схеме (1.9.25), используя таблицу функции Лапласа и принимая σ² = s ² - По найденному n ₁ и, соответственно, v ₁ = n ₁ — 1 и заданному значению

Р =1—α определяют t ₁ (по таблице распределения Стьюдента) и вычисляют и так далее.

Теперь можно снова повторить расчет по v ₂ = n ₂ — 1 и т.д.

Итерация заканчивается, если окажется n_i ≈ n_{i -1} .

Пример 1.9.7. Для определения среднего заработка работника за день при соблюдении необходимых условий было отобрано 10 работников, заработок которых оказался равным (в руб.): 325; 337; 319; 330; 327; 328; 332; 320; 318; 334. Требуется определить с вероятностью 0,95 доверительный интервал для среднего заработка работников в генеральной совокупности, если есть основания полагать, что заработная плата в генеральной совокупности подчиняется нормальному закону определения.

Решение:

По данным выборки определяем среднюю и дисперсию. Получаем

;

Рассчитываем несмещенную оценку генеральной дисперсии

Предположение о нормальном характере генерального распределения позволяет нам использовать равенства (1.9.27) и (1.9.28). Обращаясь к таблице значений функции Стьюдента, по заданным P = 2 S ( t , v )=0,95 и v = n —1 = 10 – 1 = 9 находим t = 2,26.

Вычисляем предельную ошибку выборки ε=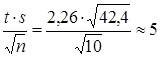(кг).

Доверительный интервал для генеральной средней:

327—5<<327+5 или 322<<332.

Пример 1.9.8. Используя данные примера 1.9.7, определить объем выборки, необходимый для того, чтобы ошибка выборочной средней с вероятностью 0,95 не превышала 3 рубля.

Решение.

Мы имеем оценку генеральной дисперсии s² = 42,4. Вначале находим n ₁ по формуле (1.9.25), принимая σ² = s ² и определяя z по таблице функции Лапласа:

Теперь обращаемся к таблице функции Стьюдента и по Р = 0,95,

v ₁ = n ₁ —1 ≈ 17 находим значение t ₁ =2,11.

Вычисляем

По Р = 0,95 и v ₂ = n ₂ —1 = 21 – 1 = 20 находим t ₂ = 2,09.

Вычисляем

Поскольку n ₃ ≈ n ₂ , то необходимый объем выборки устанавливается 21 человек.

Еще раз отметим, что рассмотренные выше схемы решения задач для малых выборок справедливы только при предположении нормального характера генерального распределения. При отсутствии такого предположения распределения неизвестно, и выборочную среднюю можно использовать лишь как точечную оценку генеральной средней без оценки точности .приближенного равенства , т. е. без расчета доверительного интервала.

3.5.3. Безвозвратная выборка

В случае безвозвратной выборки формула для среднего квадратического отклонения выборочной средней, согласно (2.21), примет вид:

(1.9.29)

Если генеральное среднее квадратическое отклонение σнеизвестно (наиболее реальная ситуация), то мы заменяем его точечной оценкой s', которая рассчитывается по формуле (1.9.20). В результате получим:

(1.9.30)

(. s — обычное «исправленное» среднее квадратическое отклонение

)

Во всем остальном ход решения задач как для случая больших выборок, так и для случая малых выборок остается прежним.

Корректирующий множитель при малой величине (например, для 1 или 5% выборок) близок к 1, и поэтому расчеты могут производиться как для возвратной выборки.