Задачи по теории управления

Рассмотрим отдельно левую часть характеристического уравнения и приведём её к общему виду:

D(p) = a₀ pⁿ + a₁ p^n-1 + a₂ p^n-2 + … + a_n-1 p + a_n .

Подставив значение p = jw, где w – угловая частота колебаний, в формулу общего вида получим характеристический комплекс:

D(jw) = X +jY,

где

X=a_n - w² a_n-2 + w⁴ a_n-4 - ..., - вещественная часть D(w) содержащая

четные степени w;

Y=w(a_n-1 - w² a_n-3 + w⁴ a_n-5 -...-мнимая часть D(w) содержащая

нечетные степени w

и заменив коэффициенты , получим

Задаваясь значениями частоты от нуля до бесконечности на комплексной плоскости построим годограф Михайлова.

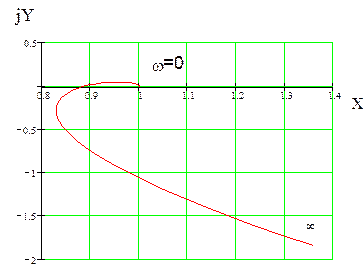Критерий устойчивости Михайлова формулируется следующим образом:

для устойчивости линейной САР необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от нуля до бесконечности, начавшись на положительной полуплоскости и не пересекая начала координат, последовательно пересек столько квадрантов комплексной плоскости, какой порядок имеет полином характеристического уравнения системы.

В нашем случае построение было прекращено, когда стало ясно, что годограф из данного квадранта не выйдет. Годограф нарушил последовательный порядок пересечения квадрантов - система будет неустойчивой.

Литература

1. Теория автоматического управления / Под ред. А.А.Воронова. - М. : Высшая школа. -1977.-Ч.I.-304с.

2. Бесекерский В.А., Попов Е.П. Теория автоматического регулирования. - М. : Наука, 1974.

3. Егоров К.В. Основы теории автоматического управления. – М. : “Энергия”, 1967