Статистические группировки по задачам, решаемым с их помощью, делятся на: типологические, структурные и аналитические.
Типологическая группировка – это разделение качественно разнородной совокупности на классы, социально-экономические типы, однородные группы единиц в соответствии с правилами научной группировки.
При проведении типологической группировки основное внимание должно быть уделено идентификации типов социально-экономических явлений. Она производится на базе глубокого теоретического анализа исследуемого явления.
Структурной называется группировка, в которой происходит разделение однородной совокупности на группы, характеризующие её структуру по какому-либо варьирующему признаку. С помощью таких группировок могут изучаться: состав предприятий по численности занятых, стоимости основных фондов, структура депозитов по сроку их привлечения и т.д. Структурная группировка представлена в расчётной части данной работы, таблица 7.
Группировка, выявляющая взаимосвязи между изучаемыми явлениями и их признаками, называется аналитической группировкой.
Всю совокупность признаков можно разделить на две группы: факторные и результативные. Факторными называются признаки, под воздействием котрых изменяются другие – они и образуют группу результативных признаков. Взаимосвязь проявляется в том, что с возрастанием значения факторного признака систематически возрастает или убывает среднее значение признака результативного.
Особенности аналитической группировки следующие: во-первых, в основу группировки кладётся факторный признак; во-вторых, каждая выделенная группа характеризуется средними значениями результативного признака.
Преимущество данного метода перед другими методами анализа связи (например, корреляционно-регрессионым) состоит в том, что он не требует соблюдения каких-либо условий для его применения, кроме одного - качественной однородности исследуемой совокупности. Аналитическая группировка приведена в расчётной части, таблица 3.
1.6.2 Статистический анализ структуры
В статистике под структурой понимают совокупность элементов социально-экономических явлений, обладающих определенной устойчивостью внутригрупповых связей, при сохранении основных свойств, характеризующих эту совокупность как целое. Статистическая структура - это распределение различных частей в пределах общего для них качества.
Статистический анализ структуры непосредственно связан с группировкой данных. Если основанием структуры выступает качественный признак, то процесс группировки не вызывает затруднений. Группировка по количественному признаку сложнее, так как требует обоснованного установления границ перехода одного качества в другое.
Статистические приемы и методы анализа позволяют проводить исследование конкретных социально-экономических структур в определённых условиях места и времени, заключающееся, прежде всего в их точном количественном измерении и соизмерении, выявления пропорций и закономерностей.
Относительный показатель структуры (ОПС) представляет собой соотношение структурных частей изучаемого объекта и их целого:
1.6.3 Показатель, характеризующий часть совокупности
ОПС = Показатель по всей совокупности в целом.
Относительный показатель структуры выражается в долях единицы или в процентах. Рассчитанные величины (di), соответственно называемые долями или удельными весами, показывают какой долей обладает или какой удельный вес имеет i-я часть в общем итоге.
Структура сложного социально-экономического явления всегда обладает той или иной степенью подвижности, имеет свойство меняться с течением времени как в количественном, так и в качественном отношении. Поэтому большое практическое значение имеют изучение структуры в динамике, оценка структурных сдвигов. При изучении структуры используются частные и обобщающие показатели структурных сдвигов. К частным показателям относятся: абсолютный прирост удельного веса, темп роста удельного веса, средний абсолютный прирост удельного веса, средний удельный вес. Среди обобщающих показателей структурных сдвигов наиболее распространены:
линейный коэффициент "абсолютных" структурных сдвигов;
квадратический коэффициент "абсолютных" структурных сдвигов;
квадратический коэффициент относительных структурных сдвигов;
линейный коэффициент "абсолютных" структурных сдвигов за n периодов.
При изучении структуры явлений и процессов следует обратить внимание на методику расчёта и экономическую интерпретацию показателей концентрации и централизации.
Оценка степени концентрации осуществляется кривой концентрации (Лоренца) и рассчитываемыми на её основе характеристиками. Для построения кривой используется частотное распределение единиц исследуемой совокупности и соответствующее ему частотное распределение изучаемого признака. Для удобства вычислений и повышения аналитичности данных единицы совокупности разбиваются на равные группы.
Наиболее известными показателями концентрации являются коэффициент Джини и коэффициент Лоренца. Данные коэффициенты принимают значения в границах от нуля до единицы и измеряют неравномерность распределения. Коэффициент Лоренца основан на прямом сравнении долей групп по числу единиц совокупности и долей по объёму признака и выражается формулой:
∑Idxi - dfiI
L = 2,
где dxi - доля i–той группы в объёме признака х;
dfi – доля i–той группы ч в числе единиц. Знаменатель коэффициента – это максимальная величина модуля.
Коэффициент Джини базируется на распределении совокупности на 10 равновеликих групп и выражении частот в процентах. Коэффициент характеризует степень неравенства в распределении объёмов признака среди единиц совокупности, степень отклонения фактического распределения объёмов признака от линии их равномерного распределения.
Централизация означает сосредоточение объёма признака у отдельных единиц и оценивается с помощью следующего показателя:
1 n +1-2∑d’xi
К = n+ n+1
Максимальное значение обобщающего показателя централизации равно 1, то есть совокупность состоит из одной единицы, обладающей всем объёмом признака. Минимальное значение приближается к нулю, но его никогда ни достигает. [2; 135]
2. Расчётная часть
2.1. Условие задач
Для анализа финансовых результатов деятельности предприятий одной из отраслей экономики произведена 10% -ная механическая выборка, в результате которой получены следующие данные млн. руб.:
| № предприятия п/п | Затраты на производство и реализацию продукции | Прибыль от продаж | № предприятия п/п | Затраты на производство и реализацию продукции | Прибыль от продаж |
| 1 | 25,2 | 4,4 | 16 | 38,1 | 4,5 |
| 2 | 46,3 | 3,7 | 17 | 48,3 | 4,2 |
| 3 | 15,4 | 5,7 | 18 | 38,3 | 4,7 |
| 4 | 18,5 | 5,9 | 19 | 29,8 | 5,5 |
| 5 | 27,1 | 4,9 | 20 | 34,3 | 3,8 |
| 6 | 27,5 | 5,6 | 21 | 21,3 | 6,9 |
| 7 | 32,0 | 6,1 | 22 | 40,0 | 6,1 |
| 8 | 29,0 | 5,2 | 23 | 35,2 | 4,0 |
| 9 | 61,4 | 3,7 | 24 | 33,4 | 6,3 |
| 10 | 53,8 | 3,5 | 25 | 24,2 | 7,7 |
| 11 | 50,5 | 4,6 | 26 | 31,6 | 6,0 |
| 12 | 49,9 | 3,5 | 27 | 42,1 | 6,0 |
| 13 | 28,5 | 5,3 | 28 | 33,8 | 5,0 |
| 14 | 41,4 | 5,1 | 29 | 32,6 | 6,1 |
| 15 | 32,7 | 6,2 | 30 | 18,6 | 5,8 |
Задание 1
Признак – затраты на производство и реализацию продукции.
Число групп – пять.
Задание 2
Связь между признаками – затраты на производство и реализацию продукции и прибыль от продаж.
Задание 3
По результатам выполнения заданий 1 с вероятностью 0,954 определите:
Ошибку выборки средней суммы затрат на производство и реализацию продукции и границы, в которых она будет находиться в генеральной совокупности.
Ошибку выборки доли предприятий с затратами на производство и реализацию продукции 43 млн. руб. и более и границы, в которых будет находиться генеральная доля.
Задание 4
Имеются следующие данные о финансовых результатах деятельности малых предприятий в области:
Отрасль экономики |
Численность работников, чел. | Прибыль отчётного периода, млн. руб. | Прибыль в расчёте на одного работника в отчётном периоде составляет от базисного уровня,% | |
| Базисный период | Отчётный период | |||
| Строительство | 13676 | 13213 | 792,8 | 90 |
| Транспорт | 1052 | 866 | 56,4 | 105 |
| Розничная торговля | 6312 |
5781 |
166,8 |
110 |
Определите:
Уровень производства прибыли на одного работника в отраслях экономики в базисном и отчётном периодах.
Отраслевую структуру численности работников малого бизнеса в каждом периоде.
Общие индексы динамики прибыли в расчёте на одного работника по трём отраслям в целом:
- переменного состава;
- фиксированного состава;
- структурных сдвигов.
Абсолютное изменение суммы прибыли в расчёте на одного работника вследствие изменения этого фактора по каждой отрасли и структурных изменений в численности работников. Сделайте выводы.
2.2 Решение задач
Задание 1.
По исходным данным:
1. Построим статистический ряд распределения предприятий по признаку затраты на производство и реализацию продукции, образовав заданное число групп с равными интервалами.
Для группировок с равными интервалами величина интервала находится по формуле: Хmax - Хmin
i = n, где
Хmax, Хmin – наибольшее и наименьшее значения признака соответственно,
n=5 – число групп.
Xmax = 61,4
Xmin = 15,4
Тогда 61,4 – 15,4
i = 5 = 9,2
Отсюда путём прибавления величины интервала к минимальному уровню признака в группе получим следующие группы предприятий по размеру затрат на приозводство и реализацию продукции (табл.1).
Таблица 1.
Распределение предприятий по размеру затрат.
| № п/п | Группы предприятий по размеру затрат, млн. руб. | Число предприятий | |
| В абсолютном выражении, ед. | В относительных единицах,% | ||
| 1 | 15,4 – 24,6 | 5 | 16,7 |
| 2 | 24,6 – 33,8 | 12 | 40,0 |
| 3 | 33,8 – 43,0 | 7 | 23,3 |
| 4 | 43,0 – 52,2 | 4 | 13,3 |
| 5 | 52,2 – 61,4 | 2 | 6,7 |
| Итого | 30 | 100,0 | |
Данные группировки показывают, что около 44% предприятий имеют затраты свыше 33,8 млн. руб.
2. Построим графики полученного ряда распределения. Графически определим значения моды и медианы.
1) Построим гистограмму и определим значение моды (рис.1). Первоначально по наибольшей частоте признака определим модальный интервал. Наибольшее число предприятий – 12 – затрачивают на производство и реализацию продукции сумму в интервале 24,6-33,8 млн. руб., который и является модальным. Для определения значения моды правую вершину модального прямоугольника соединим с верхним правым углом предыдущего прямоугольника, а левую вершину – с верхним левым углом предшествующего. Абсцисса точки пересечения этих прямых будет мода. Мо ≈ 31 млн. руб. – наиболее часто встречающееся значение признака.
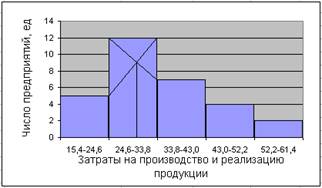
Рис.1. Гистограмма распределения предприятий по затратам на производство и реализацию продукции.
2) Для определения значения медианы построим кумуляту распределения предприятий по затратам на производство и реализацию продукции (Рис.2).
Определим медианный интервал, таким интервалом очевидно будет интервал затрат 24,6-33,8 млн. руб., так как его кумулятивная частота равна 17 (5+12), что превышает половину суммы всех частот (30: 2=15).
Далее определим ординаты накопленных частот в пределах 24,6-33,8, это будет у1 = 29, у2 = 40 и у3 = 32. Найдём середину промежутка ординат накопленных частот в пределах 24,6-33,8:
у1+у2+у3 29+40+32
Уср = 3 = 3 = 33.
Абсцисса середины промежутка есть медиана. Ме ≈ 33.
Полученный результата говорит о том, что из 30 предприятий 15 имеют затраты на производство и реализацию продукции менее 33 млн. руб., а 15 предприятий – более.
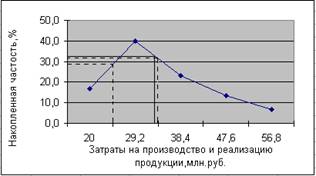
Рис.2. Кумулята распределения предприятий по затратам на производство и реализацию продукции.
3. Основные характеристики интервального ряда распределения. Вспомогательные расчёты представлены в таблице 1.1.
Таблица 1.1.
| №п/п | Затраты на производство и реализацию продукции, млн. руб., х | Число предприятий, f | Середины интервалов х |
х*f | (x-xср) 2 | (x-xср) 2*f |
| 1 | 15,4 - 24,6 | 5 | 20 | 100 | 199,00 | 994,9902 |
| 2 | 24,6 - 33,8 | 12 | 29,2 | 350,4 | 24,08 | 288,90 |
| 3 | 33,8 - 43,0 | 7 | 38,4 | 268,8 | 18,43 | 129,03 |
| 4 | 43,0 - 52,2 | 4 | 47,6 | 190,4 | 182,07 | 728,28 |
| 5 | 52,2 - 61,4 | 2 | 56,8 | 113,6 | 514,99 | 1029,97 |
| Итого | 30 | 192 | 1023,2 | 938,5636 | 3171,18 | |
| Среднее | 34,11 | |||||
| Среднее квадратическое. | 10,28 | |||||
| Коэффициент вариации | 30,14 |
1) Средняя арифметическая ∑х*f
хср = ∑f
1023,2
хср = 30 = 34,1 (млн. руб)
Соотношение между модой, медианой и средней характеризуют форму распределения. Если IМо-хсрI ≈ 3*IМе-хсрI
I31 – 34,1I ≈ 3*I33 – 34,1I
3,1 ≈ 3,3, то распределение близко к нормальному.
Так как Мо < Ме < хср, 31 < 33 < 34,1, то асимметрия правосторонняя.
∑(х-хср) 2*f
2) Среднее квадратическое отклонение σ = √ ∑f
3171,18
σ = √ 30 = 10,28 (млн. руб)
σ
3) Коэффициент вариации V = xср *100
10,28
V = 34,1 *100 = 30,14%.
4. Рассчитаем среднюю арифметическую затрат на производство и реализацию продукции по исходным данным.
∑х 1040,8
хср = n= 30 = 34,7 (млн. руб)
Между средней арифметической по исходным данным и средней арифметической ряда распределения существует некоторое расхождение, так как во втором случае делается предположение о равномерности распределения единиц признака внутри группы
Задание 2
По исходным данным:
1. Установим наличие и характер связи между признаками затраты на производство и реализацию продукции и прибыль от продаж, образовав заданное число групп с равными интервалами по обоим признакам, методами:
а) аналитической группировки,
б) корреляционной таблицы.
1. Аналитическая группировка.
Выбираем факторные и результативные признаки, подсчитываем число единиц в каждой из образованных групп, определим объём варьирующих признаков в пределах созданных групп, средние размеры результативного показателя и построим рабочую таблицу 2.1. (интервалы возьмём из задания 1, п.1).
Таблица 2.1.
Распределение предприятий по величине затрат на производство и реализацию продукции
| № п/п | Группы предприятий по величине затрат на производство и реализацию продукции. | № предприятия | Затраты на производство и реализацию продукции | Прибыль от продаж |
| 3 | 15,4 | 5,7 | ||
| 4 | 18,5 | 5,9 | ||
| 1 | 15,4 – 24,6 | 21 | 21,3 | 6,9 |
| 25 | 24,2 | 7,7 | ||
| 30 | 18,6 | 5,8 | ||
| Итого | 5 | 98 | 32 | |
| 1 | 25,2 | 4,4 | ||
| 5 | 27,1 | 4,9 | ||
| 6 | 27,5 | 5,6 | ||
| 7 | 32,0 | 6,1 | ||
| 8 | 29,0 | 5,2 | ||
| 2 | 24,6 – 33,8 | 13 | 28,5 | 5,3 |
| 15 | 32,7 | 6,2 | ||
| 19 | 29,8 | 5,5 | ||
| 24 | 33,4 | 6,3 | ||
| 26 | 31,6 | 6,0 | ||
| 28 | 33,8 | 5,0 | ||
| 29 | 32,6 | 6,1 | ||
| Итого | 12 | 363,2 | 66,6 | |
| 14 | 41,4 | 5,1 | ||
| 16 | 38,1 | 4,5 | ||
| 18 | 38,3 | 4,7 | ||
| 3 | 33,8 – 43,0 | 20 | 34,3 | 3,8 |
| 22 | 40,0 | 6,1 | ||
| 23 | 35,2 | 4,0 | ||
| 27 | 42,1 | 6,0 | ||
| Итого | 7 | 269,4 | 34,2 | |
| 2 | 46,3 | 3,7 | ||
| 11 | 50,5 | 4,6 | ||
| 4 | 43,0 – 52,2 | 12 | 49,9 | 3,5 |
| 17 | 48,3 | 4,2 | ||
| Итого | 4 | 195 | 16 | |
| 5 | 52,2 – 61,4 | 9 | 61,4 | 3,7 |
| 10 | 53,8 | 3,5 | ||
| Итого | 2 | 115,2 | 7,2 | |
| Всего | 30 | 1040,8 | 156 |
Для определения наличия и характера связи между затратами на производство и реализацию продукции и прибылью от продаж по данным рабочей таблицы строим итоговую аналитическую таблицу (табл.3).
Таблица 3.
Зависимость прибыли предприятий от затрат на производство и реализацию продукции.
| № п/п | Группы предприятий по величине затрат на производство и реализацию продукции. | Число предприятий | Затраты на производство и реализацию продукции | Прибыль от продаж | ||
| всего | средние затраты | всего | в среднем на предприятие | |||
| 1 | 15,4 – 24,6 | 5 | 98 | 19,6 | 32 | 6,4 |
| 2 | 24,6 – 33,8 | 12 | 363,2 | 30,3 | 66,6 | 5,6 |
| 3 | 33,8 – 43,0 | 7 | 269,4 | 38,5 | 34,2 | 4,9 |
| 4 | 43,0 – 52,2 | 4 | 195 | 48,7 | 16 | 4 |
| 5 | 52,2 – 61,4 | 2 | 115,2 | 57,6 | 7,2 | 3,6 |
| Итого в целом по сов-ти | 30 | 1040,8 | 34,7 | 156 | 5,22 | |
Данные таблицы показывают, что с ростом затрат на производство и реализацию продукции, осуществляемые предприятиями средние затраты, прибыль от продаж уменьшается. Следовательно, между исследуемыми признаками существует обратная корреляционная зависимость.
Вычислим эмпирические показатели для признака "прибыль от продаж".
1) Общая дисперсия:
∑( xi – хср) 2 32,99
σо 2 = n= 30 = 1,1
2) Межгрупповая дисперсия:
∑( xj – xjср) 2* nj20,61
δ2 = ∑ nj= 30 = 0,687
3) Коэффициент детерминации:
δ2 0,687
η2 = σо 2 = 1,1 = 0,62, или 62%.
Он показывает, что прибыль от продаж на 62% зависит от затрат на производство и реализацию продукции и на 38% - от других внутриотраслевых причин.
4) Эмпирическое корреляционное отношение составляет η = √0,62 = 0,79, что свидетельствует о существенном влиянии на дифференциацию прибыли от продаж отраслевых особенностей.
2. Корреляционная таблица.
Сначала построим интервальный ряд распределения предприятий по признаку прибыль от продаж (табл.4). Величина интервала равна:
7,7-3,5
i = 5 = 0,84
Таблица 4.
Распределение предприятий по величине прибыли от продаж.
| № п/п | Группы предприятий по прибыли от продаж, млн. руб. | Число предприятий | |
| В абсолютном выражении, ед. | В относительных единицах,% | ||
| 1 | 3,5-4,34 | 7 | 23,3 |
| 2 | 4,34-5,18 | 7 | 23,3 |
| 3 | 5,18-6,02 | 10 | 33,3 |
| 4 | 6,02-6,86 | 4 | 13,4 |
| 5 | 6,86-7,7 | 2 | 6,7 |
| Итого | 30 | 100,0 | |
Построим корреляционную таблицу, образовав пять групп по факторному и результативному признакам (табл.5).
Таблица 5.
Распределение предприятий по величине затрат на производство и реализацию продукции и прибыли от продаж.
| Затраты на производство и реализацию продукции, млн. руб. | Прибыль от продаж, млн. руб. | |||||
| 3,5 – 4,34 | 4,34 – 5,18 | 5,18 – 6,02 | 6,02 – 6,86 | 6,86 – 7,7 | Итого | |
| 15,4 – 24,6 | 3 | 2 | 5 | |||
| 24,6 – 33,8 | 3 | 6 | 3 | 12 | ||
| 33,8 – 43,0 | 2 | 3 | 1 | 1 | 7 | |
| 43,0 – 52,2 | 3 | 1 | 4 | |||
| 52,2 – 61,4 | 2 | 2 | ||||
| Итого | 7 | 7 | 10 | 4 | 2 | 30 |
Как видно из данных таблицы распределение числа предприятий произошло вдоль диагонали, проведённой из левого нижнего угла в правый верхний угол таблицы, то есть уменьшение признака "затраты на производство и реализацию продукции" сопровождалось увеличением признака "прибыль от продаж". Характер концентрации частот по диагонали корреляционной таблицы свидетельствует о наличии обратной тесной корреляционной связи между изучаемыми признаками.
Задание 3
С вероятностью 0,954 определить:
Ошибку выборки средней суммы затрат на производство и реализацию продукции и границы, в которых она будет находиться в генеральной совокупности.
Ошибку выборки доли предприятий с затратами на производство и реализацию продукции 43 млн. руб. и более и границы, в которых будет находиться генеральная доля.
![]() 1) Ошибка выборки средней суммы затрат на производство и реализацию продукции
1) Ошибка выборки средней суммы затрат на производство и реализацию продукции
![]() Δх = t * √σ2 / n * (1 – n / N); n / N = 0,1, так как выборка 10% -ая
Δх = t * √σ2 / n * (1 – n / N); n / N = 0,1, так как выборка 10% -ая
Δх = 2 * √105,42 / 30 * (1 – 0,1) = 3,557
2) Границы, в которых будет находиться средняя сумма затрат на производство и реализацию продукции в генеральной совокупности
_ _ _
x – Δх ≤ x ≤ x + Δх
_
34,41 – 3,557 ≤ x ≤ 34,41 + 3,557
_
30,857 ≤ x ≤ 37,970
3) Ошибку выборки доли предприятий с затратами на производство и реализацию продукции 43 млн. руб. и более
предприятий с затратами на производство и реализацию продукции 43 млн. руб. и более – 6
ω = 6/30 = 0,2
Δω = t √(ω * (1 – ω) / n * (1 – n/N)) ![]()
Δω = 2 √0,2 * 0,8 * 0,9 / 30 = 0,1386 или 13,86%
4) границы, в которых будет находиться генеральная доля.
ω – Δω ≤ р ≤ ω + Δω
20 – 13,86 ≤ р ≤ 20 + 13,86
6,14 ≤ 20 ≤ 33,86
С вероятностью 0,954 ошибка выборки средней суммы затрат на производство и реализацию продукции составит 3,3661 млн. руб. Средние затраты на производство и реализацию продукции в генеральной совокупности находятся в интервале от 30,7439 млн. руб. до 37,4761 млн. руб.
Ошибка доли выборки предприятий с затратами на производство 43 млн. и более составит 13,86%, доля предприятий с затратами на производство 43 млн. руб. и более будет находиться в пределах от 6,14 до 33,86
Задание 4.
1. Определим уровень производства прибыли на одного работника в отраслях экономики в базисном и отчётном периодах (табл.6, прил.2). В виде расчётных формул таблица 6.1., приложение2.
2. Отраслевая структура численности работников малого бизнеса в каждом периоде (табл.7). В виде расчётных формул таблица 7.1., приложение2. Для отображения отраслевой структуры используем относительный показатель структуры, который представляет собой отношение части единиц совокупности (fi) ко всему объёму совокупности (∑fi):
d = (fi / ∑fi) * 100%, где d – удельный вес частей совокупности.
В данном примере относительные показатели структуры равны:
dо = То/∑То *100% - в базисном периоде.
d1 = Т1/∑Т1 * 100% - в отчётном периоде.
Таблица 7.
Отраслевая структура численности работников малого бизнеса в каждом периоде.
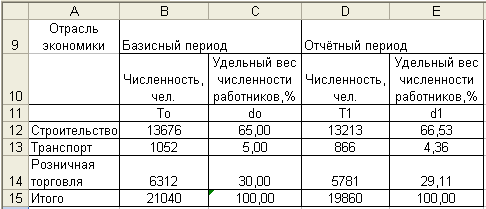
Данные таблицы свидетельствуют о том, что удельный вес численности работников в строительной отрасли в отчётном периоде вырос по сравнению с базисным периодом, а удельный вес численности работников в розничной торговле и транспортной отрасли в отчётном периоде уменьшился по сравнению с базисным.
4. Общие индексы динамики прибыли в расчёте на одного работника по трём отраслям в целом. Построим систему индексов
8-09-2015, 11:49
