ДЕПАРТАМЕНТ ВЫСШИХ УЧЕБНЫХ ЗАВЕДЕНИЙ
Волгоградская государственная сельскохозяйственная академия
Кафедра: _____________________
Дисциплина: Инженерная геодезия
КОНТРОЛЬНАЯ РАБОТА
Выполнила: студентка третьего курса,
заочного отделения, группы 32 ЭМЗ, 04/040
Фастова Надежда Александровна
Волгоград 2006г.
ЗАДАНИЕ 1
В задание входит решение 3-х задач по теории ошибок. Задача 1 относится к типу задач на равноточные измерения, задача 2 – на неравноточные измерения и задача 3 – на оценку точности функций измеренных величин.
При решении задач по теории ошибок пользуются формулами, приведенными ниже, в которых приняты следующие обозначения:
Х – истинное значение измеряемой величины;
Β,L,H – результат измерения расстояния, угла или высоты;
n – число измерений;
p – вес результата измерений;
l о – вероятнейшее значение результата измерения,
∆ =l –Х – истинная ошибка результата измерений;
v=l-lo – отклонение результата измерения от вероятнейшего значения;
ср.кв. ош. – средняя квадратическая ошибка;
m– ср.кв.ош. одного измерения, вычисленная из ряда измерений;
![]() – ср.кв.ош. единицы веса;
– ср.кв.ош. единицы веса;
М – ср.кв.ош. вероятнейшего значения;
1/N – относительная ошибка.
Непосредственные измерения
| Название формулы | Измерения | |
| равноточные | неравноточные | |
| Вероятнейшее значение | Lо
= Lo
= |
Lo
= Lo
= |
| Ср.кв. ошибка одного измерения | m= m= |
|
| Ср.кв. ошибка единицы веса | ||
| Ср.кв.ош. вероятнейшего значения | M= |
M= |
| Зависимость между весом и ср.кв.ош., где с–произв. пост.число | Р= |
|
*Если значение m неизвестно, то величина веса p назначается по формулам для нивелирования p=![]() или p=
или p=![]() ;
;
где l – число километров в ходе, n – число станций в ходе; для угловых измерений
P=c*k,
где к – число приемов при измерении угла.
Задача 1а (вариант 0, т.к последняя цифра 40)
Расстояние измерялось стальной двадцатиметровой лентой 3 раза. Требуется определить:
1) вероятнейшее значение расстояния;
2)ср.кв.ош. одного измерения;
3)ср.кв.ош. вероятнейшего значения;
4) относительную ошибку окончательного результата.
Схема решения задачи:
| Номера измерений | Результаты измерений, м | v=l-lo , см | V2 |
| 1 | 248,7 | 7 | 49 |
| 2 | 248,56 | -7 | 49 |
| 3 | 248,63 | 0 | 0 |
| lo | 248,63 |
Решение:
1) Lo
=![]() =
=![]() ;
;
2) m=![]() =
=![]() см;
см;
3) M=![]() =
=![]() см;
см;
4) ![]() .
.
Ответ: Lo =248,63; m =+-7 см; M =+-4,042 см; 1/6151,2.
Задача 1б
От трех реперов проложены нивелирные ходы к новому реперу, по каждому ходу определена высота этого репера.
| Номер хода | Высота репера Н | Длина хода l , км |
| 1 | 181,525 | 2 |
| 2 | 181,518 | 4 |
| 3 | 181,507 | 5 |
Определить вероятнейшее значение высоты репера и ее среднюю квадратическую ошибку.
За вес – р нивелирного хода следует принять величину обратную длине хода l .
Схема задачи:
| № хода | Высота репера, Н | Длина хода l , км | Вес р= |
V= H-Ho | pv | pv2 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 181,525 | 2 | 0,5 | 5 | -2,5 | 12,5 |
| 2 | 181,518 | 4 | 0,25 | -8 | 2 | 16 |
| 3 | 181,507 | 5 | 0,2 | -13 | 2,6 | 33,8 |
| 181,52 | 0,95 | 4,6 и -2,5 | 62,3 |
Решение:
1) по формуле Но
=![]() находим вероятнейшее значение
находим вероятнейшее значение ![]() =0 (или близко к нулю);
=0 (или близко к нулю);
Но
= ![]()
Р1
=![]() =2/4=0,5;
=2/4=0,5;
Р2
=![]() =4/16=0,25;
=4/16=0,25;
Р3
=![]() =5/25=0,2.
=5/25=0,2.
![]() =0,95.
=0,95.
2) ср.кв.ош. веса:
![]()
![]() =
=![]() мм;
мм;
V= H-Ho
V1 =(181,525-181,52)*1000=5,
V2 =-8,
V3 =-13.
рv1 =-2,5, pv2 =2, pv3 =2,6.
pv2 1 =12,5, pv2 2 =16, pv2 3 =33,8.
M=![]() =
=![]() мм.
мм.
Ответ: Но
=181,52; ![]() +-5,58 мм;
M
=+-5,72 мм.
+-5,58 мм;
M
=+-5,72 мм.
Задача 1в
Вариант 0
Пронивелирован ход между реперами 1,23,4. Вычислить сумму превышений между реперами 1 и 4 и ее среднюю квадратическую ошибку, если:
h 1.2 =2,781 м, m 1,2 =+-9 мм;
h 2,3 = -3,517 м, m 2,3 =+-7 мм,
h 3,4 =1,284 м. m 3,4 =+-10 мм.
Решение:
h 1.4 = h 1.2 + h 2,3 + h 3,4 =0,548 м,
M=![]() =
=![]() мм.
мм.
Ответ: h 1.4 =0,548м, M =+-15 мм.
ЗАДАНИЕ 2
Построение поперечного масштаба и отложение по нему отрезков линий в различных масштабах.
Вариант 0
| Масштаб | расстояние |
| 1/2000 | 138,42 |
| 1/5000 | 127,54 |
| 1/10000 | 378,34 |
1. 1 см на плане соответствует 50 м на местности;
2. 1 см на плане соответствует 20 м на местности;
3. 1 см на плане соответствует 100 м на местности.
(Чертеж прилагается).
ЗАДАНИЕ 3
Камеральная обработка результатов съемки.
1. Вычислить координаты точек теодолитных ходов: замкнутого и диагонального.
2. По вычисленным координатам точек составить план в масштабе 1/2000 и по данным абриса съемки нанести ситуацию на план.
Результаты измерений и исходные данные:
а)величины углов и горизонтальных проложений, полученные в результате измерений:
| № точек | Измеренные углы | Длины сторон, м |
| 1 | 95 59 | 224,99 |
| 2 | 83 08 | 201,94 |
| 3 | 128 46 | 208,04 |
| 4 | 78 37 | 126,70 |
| 5 | 152 29 | 192,47 |
| 1 | ||
| Диагональный ход | ||
| 4 | ||
| 5 | 90 34 | 130,33 |
| 6 | 208 30 | 189,65 |
| 2 | 33 30 | |
| 3 | ||
б)дирекционный угол ![]() =277 46 начальной стороны;
=277 46 начальной стороны;
в) координаты точек 1: Х1 =8 000,00; У1 =6 000,00;
г) схема теодолитного хода на рис.
д) горизонтальные углы измерены теодолитом Т30.
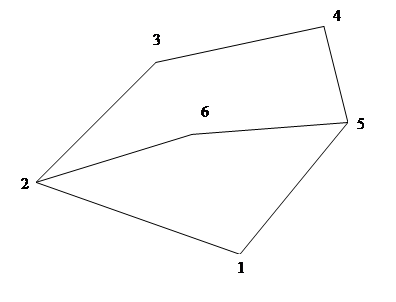
Рис. Схема съемочного обоснования
1. Вычисление координат точек теодолитного хода
Запись исходных данных в ведомость ординат
Последовательность вычислений:
Определение угловой невязки и распределение поправок в углы.
Суммируют величины всех измеренных углов полигона и записывают практическую сумму ![]() под общей чертой. Затем вычисляют теоретическую сумму углов полигона по формуле:
под общей чертой. Затем вычисляют теоретическую сумму углов полигона по формуле:
![]() , где
n
– число углов теодолитного хода.
, где
n
– число углов теодолитного хода.
Угловая невязка теодолитного хода:
![]()
Вычисленная угловая невязка не должна превышать предельную:
Пред. ![]()
Для теодолита Т30
m
=0,5. Тогда ![]() .Если полученная невязка окажется меньше предельной, то поправки вводятся на все измеренные углы, учитывая следующие правила:
.Если полученная невязка окажется меньше предельной, то поправки вводятся на все измеренные углы, учитывая следующие правила:
1. поправки имеют знак, обратный знаку невязки;
2. поправки вводятся поровну во все измеренные углы. Для простоты вычислений допускается введение таких поправок, чтобы исправленные значения углов имели целое число минут;
3. абсолютная сумма поправок должен быть равна невязке.
Сумма исправленных углов должна равняться сумме углов полигона.
Вычисление дирекционных углов теодолитного хода
Дирекционные углы для каждой стороны вычисляют по формуле:
![]() , где
, где ![]() – дирекционный угол предыдущей стороны ход;
– дирекционный угол предыдущей стороны ход;
![]() – дирекционный угол последующей стороны;
– дирекционный угол последующей стороны;
![]() – исправленный угол, лежащий вправо по ходу между стороной с известным дирекционным углом и следующей стороной.
– исправленный угол, лежащий вправо по ходу между стороной с известным дирекционным углом и следующей стороной.
Например, если ![]() – известен, то
– известен, то ![]() будет равен
будет равен ![]() , где
, где ![]() – угол при второй точке. Дирекционные углы всех последующих сторон вычисляются в том же порядке. Контролем правильности вычисления дирекционных углов является получение исходного дирекционного угла через дирекционный угол последней стороны и первый исправленный угол.
– угол при второй точке. Дирекционные углы всех последующих сторон вычисляются в том же порядке. Контролем правильности вычисления дирекционных углов является получение исходного дирекционного угла через дирекционный угол последней стороны и первый исправленный угол.
277 46,00+180=457 46-83 08=374 38-360=14 38 +180=194 38-128 46=65 52 +180=245 52-78 37=167 15 +180=347 15-152 29=193 46.
167 15+180=347 15-90 35=256 40 +180=436 40-208 31=228 09.
Если дирекционный угол получается больше 360о
, как ![]() , то необходимо из него вычесть 360о
. Если после прибавки 180о
к дирекционному углу исправленный угол не вычитается из него, то необходимо добавить еще 360о
, а затем вычитать исправленный угол
, то необходимо из него вычесть 360о
. Если после прибавки 180о
к дирекционному углу исправленный угол не вычитается из него, то необходимо добавить еще 360о
, а затем вычитать исправленный угол ![]() . В конце вычислений необходимо получить исходный дирекционный угол.
. В конце вычислений необходимо получить исходный дирекционный угол.
Вычисление румбов
Вычисленные дирекционные углы переводят в румбы по одной из формул, данных на рисунке, в зависимости от величины дирекционного угла.
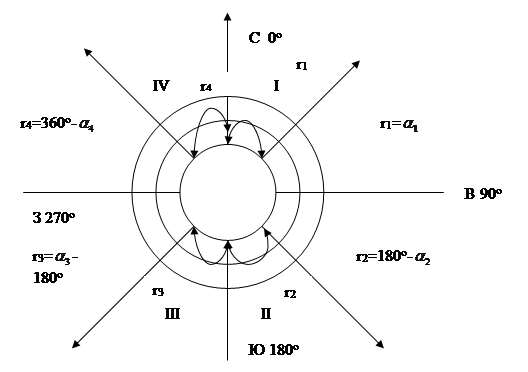
Рис. Зависимость между дирекционными углами и румбами.
r2 =180-167 15=12 45;
r3 =193 46-180=13 46; r3 =256 40-180=76 40; r3 =228 09-180=48 09;
r4 =360-277 46=82 14.
Вычисление приращений координат, невязок и координат точек.
Приращение координат ∆Х и ∆У есть разности координат двух точек по оси Х и по оси У. Приращения координат по абсолютной величине вычисляют по формулам:
∆
Х
=/d*cos![]() /=/d*cos r/;
/=/d*cos r/;
∆
У
=/d*sin![]() /=/d*sin r/;
/=/d*sin r/;
где d – горизонтальное проложение;
![]() – дирекционный угол;
– дирекционный угол;
r – румб.
Для нахождения cos r и sin r – значений тригонометрических функций румба линии используют «Пятизначную таблицу тригонометрических функций». Горизонтальное проложение следует умножить на все пятизначное число, выражающее синус или косинус, а результат округлить до сотых долей метра.
∆Х
1. 224,99* cos82 14=224,99*0,1363=30,66,
2. 201,94* cos14 38=201,94*0,9678=195,44,
3. 208,04* cos65 52=208,04*0,4078=84,84,
4. 126,70* cos12 45=126,70*0,9757=123,62,
5. 192,47* cos13 46=192,47*0,9710=186,89,
6. 130,33* cos76 40=130,33*0,2294=29,90,
7. 189,65* cos48 09=189,65*0,6671=126,51.
∆У
1. 224,99* sin82 14=224,99*0,9908=222,92,
2. 201,94* sin14 38=201,94*0,2527=51,03,
3. 208,04* sin65 52=208,04*0,9126=189,86,
4. 126,70* sin12 45=126,70*0,2207=27,96,
5. 192,47* sin13 46=192,47*0,2379=45,79,
6. 130,33* sin76 40=130,33*0,9731=126,82,
7. 189,65* sin48 09=189,65*0,7449=141,27.
Перед значениями ∆Х и ∆У ставят знак плюс (+) или минус (-) согласно названию румба:
| Название румбов | Знак приращения координат | |
| ∆Х | ∆У | |
| 1 | 2 | 3 |
| СВ | + | + |
| ЮВ | - | + |
| ЮЗ | - | - |
| СЗ | + | - |
Затем подсчитывают алгебраические суммы для ∆Х и
∆У. Теоретическая сумма приращений замкнутого хода должна равняться нулю, т.е. ![]() ,
, ![]() . Из-за неизбежности случайных ошибок измерений это условие не выполняется и величины сумм ∆Х и ∆У будут являться невязками по оси Х и по оси У.
. Из-за неизбежности случайных ошибок измерений это условие не выполняется и величины сумм ∆Х и ∆У будут являться невязками по оси Х и по оси У.
Абсолютная невязка теодолитного хода представляет собой гипотенузу прямоугольного треугольника с катетами, равными
fx
и
fy
,, т.е.
f
абс
=![]() . Допустимость этой невязки определяется относительной невязкой, которая не должна превышать 1/1500 при измерении расстояний 20-метровой стальной лентой.
. Допустимость этой невязки определяется относительной невязкой, которая не должна превышать 1/1500 при измерении расстояний 20-метровой стальной лентой.
Для определения относительной невязки подсчитывают периметр теодолитного хода с округлением до сотен метров и вычисляют ее по формуле f абс /Р.
После подсчета относительной невязки следует невязки fx и fy распределить в виде поправок соответственно на все ∆Х и ∆У.
Суммы исправленных ∆Х и ∆У должны равняться нулю.
Координаты точек вычисляются по формулам:
![]()
![]()
Контролем служит получение заданных координат точки №1.
Вычисление координат точек диагонального хода.
Координаты точек диагонального хода вычисляют в той же последовательности, что и для замкнутого теодолитного хода. Некоторые различия в вычислениях заключаются в следующем:
1. Теоретическую сумму углов диагонального ход подсчитывают по формуле:
![]() , где
, где ![]() и
и ![]() – соответственно начальный и конечный дирекционные углы.
– соответственно начальный и конечный дирекционные углы.
N – число измеренных углов.
2. Теоретическую сумму приращений вычисляют по формулам:
∑![]() ;
; ![]() , где Хн
,Ун
,Хк
,Ук
– координаты начальной и конечной точек, т.е. точек 5 и 2.
, где Хн
,Ун
,Хк
,Ук
– координаты начальной и конечной точек, т.е. точек 5 и 2.
3. Невязку в приращениях координат вычисляют по формулам:
fx
=![]() fy
=
fy
=![]() .
.
![]()
![]() =332 34,
=332 34, ![]() 332 37.
332 37. ![]() = - 3.
= - 3.
Доп ![]() =1,5
=1,5![]() =+-2,5. Р=319,98.
=+-2,5. Р=319,98.
![]() =- 156,41,
=- 156,41, ![]() = - 268,09.
= - 268,09.
![]() = 38,95,
= 38,95, ![]() = - 217,75
= - 217,75
fx =8186,98-29,90=81157,08-126,51=8030,57-8225,93= - 195,36,
fy =6045,82-126,82=5919-141,27=5777,73-5828,07= - 50,34.
fx
=![]() = - 156,41-38,95= - 195,36,
= - 156,41-38,95= - 195,36,
fy
=![]() = - 268,09+217,75= - 50,34.
= - 268,09+217,75= - 50,34.
fабс
=![]() =201,74.
=201,74.
(Таблица-ведомость прилагается).
Построение плана. Построение координатной сетки.
(чертеж прилагается)
ЗАДАНИЕ 4
1. В журнале продольного нивелирования надо вычесть отметки всех пронивелированных точек и провести контроль вычислений.
2. На основании данных обработанного журнала построить продольный профиль трассы и поперечник; на профиль нанести проектную линию, вычислить рабочие отметки и определить расстояния до точек нулевых работ.
Вычисление превышений между связующими точками (пикетными и иксовыми)
Так как пикетные точки нивелировались по способу «из середины», то превышение между ними вычисляют по формуле:
H =а-в, где H – превышение;
а – отсчет на заднюю рейку;
в – отсчет на переднюю рейку.
Вариант 40-49.
(Вариант 40)
Ст.1
H=966-1662= - 696 мм,
H=5649-6343= -694 мм.
Расхождение: - 696+694= -2 мм – допустимое.
Ср. превышение: (696+694)/2=695.
Ст.2.
H=2612-888=1724, H=7296-5568=1728.
Ст.3.
H=2721-990=1731, H=7401-5671=1730.
Ст.4.
H=712-1956= - 1244, H=5395-6636= -1241.
Ст. 5.
H=474-2856= -2382, H=5156-7540= -2384.
Ст. 6.
H=593-1846= - 1253, H=5277-6530= -1253.
Вычисление невязки в превышениях и ее распределение.
Полученная сумма всех средних превышений теоретически должна быть равна разности отметок конечного и начального реперов. Практически же вследствие ошибок в измерениях получается невязка, которая подсчитывается по формуле:
fh
=
![]() . Невязка равна разности между алгебраической суммой средних превышений и разностью отметок конечного и начального реперов.
. Невязка равна разности между алгебраической суммой средних превышений и разностью отметок конечного и начального реперов.
Допустимость невязки проверяют по формуле:
Пред.
Fh
=30 мм![]() . Где 1–число километров нивелирного хода.
. Где 1–число километров нивелирного хода.
В нашем примере оно = 0,5.
Пред. Fh=+-21 мм, а наша невязка 15 мм меньше предельной, следовательно ее можно распределить.
Вычисление отметок связующих точек
Отметки связующих точек вычисляют последовательно от известной отметки начального репера по формуле Н n = Hn -1 + h , т.е. отметка следующей точки равна отметке данной точки плюс исправленное превышение между этими точками.
ППКО: Но =Нн +hн-о
91,608+0,697=90,911.
Отметка точки Х равна:
Нх =Но +hо-х
90,911+1,724=92,635.
Отметка ПК1
Н3 =Нх + hх-3
92,635+1,728=94,363.
Отметка ПК2
Н2 =Н1 + h1-2
94,363+(-1,245)=93,118.
Отметка ПК3
Н3 =Н2 + h2-3
93,118+(-2,386)=90,732.
Следует помнить, что отметки записывают в метрах, а вычисленные в журнале превышения получают в миллиметрах, поэтому при вычислении отметок превышения необходимо выражать в метрах.
Контролем правильности вычисления отметок связующих точек является получение точного значения Н Rp 2 , вычисленного по исправленным превышениям.
Вычисление отметок промежуточных точек (плюсовых и точек поперечников).
Отметки этих точек определяют через горизонт нивелира.
Горизонтом нивелира называют высоту луча визирования над уровенной поверхностью или отметку луч визирования.
ГН=На +а, ГН=Нв +в.
где На – отметка задней связующей точки;
а – отсчет по рейке на этой точке, взятый по рабочей стороне, или
где Нв – отметка передней связующей точи;
в – отсчет по рейке на этой точке, взятый по рабочей стороне.
Отметка плюсовой точки С равна
Нс =ГН-с,
где с – отсчет по рейке на данную плюсовую точку.
Так все промежуточные точки нивелируют только по рабочей стороне рейки, то для вычисления горизонта нивелира на станции используют отсчеты, взятые по рабочей стороне реек.
Ст. 4.
ГН=94,363+0,712=95,075 ГН=93,118+1,956=95,074.
Ср. (95,075+95,074)/2=95,074.
Отметка плюсовой точки
ПК1+68
95,074-1,518=93,556.
ГН=93,118+0,474=93,592 м, ГН=90,732+2,856=93,588 м. ГНср=93,59.
Отметка точки ПР6,8
93,59-1,215=92,375 м.
ПР20
93,59-2,496=91,094 м.
Лв 12,6
93,59-0,785=92,805 м.
Лв 20
93,59-0,447=93,143 м.
Построение продольного профиля.
После вычисления отметок всех пронивелированных точек приступают к построению продольного профиля и поперечников. Масштабы: 1/1000, 1/2000, 1/5000, 1/10 000 для горизонтальных линий.
Масштабы для вертикальных линий в 10 раз больше.
Рекомендуемые масштабы: для горизонтальных линий: 1/2000; для вертикальных 1/200.
Положение начала и конца кривой.
Угол поворота 36 40, следовательно Т (тангенс) 331,364. кривая (К)=639,954, домер Д=2Т-К=22,774, биссектриса Б– =53,471. При радиусе 1000 м.
Так как наш радиус 100 м. то все значения надо уменьшить в 10 раз, т.о. для угла 36 40: Т=33,14, К=63,99, Б=5,35, Д=2,28.
Для определения положения начала и конца делают следующие подсчеты:
– выписывают расстояние до угла поворота ПК3+6,8;
– вычитают тангенс Т-33,14;
–получают расстояние до начала кривой НК=ПК2+73,66;
– прибавляют длину кривой К+63,99;
– получают расстояние до конца кривой КК=ПК3+37,65.
Проведение проектной линии
На профиль наносят проектную линию строящегося сооружения. Для этого необходимо вычислить и подписать ее отметки в каждой из нанесенных на профиле точек в соответствующей графе профильной сетки. Исходными данными для вычисления проектных отметок являются: заданная проектная отметка начальной точки, проектируемые уклоны и длинны участков проектной линии.
Уклон линии равен тангенсу угла наклона этой линии или, (рис) уклон есть отношение превышения к горизонтальному проложению линии, или
i=tgv=h/d,
где I – продольный уклон линии АВ;
v – угол наклона линии АВ к горизонту;
h – превышение между точками А и В;
d – горизонтальное проложение линии АВ.
Если известен уклон I и горизонтальное проложение d , то превышение между точками А иВ будет равно:
h=i*d
Следовательно, если отметка точки А известна, то отметку точки В вычисляют так:
Нв =На +- h или Нв =На +- i * d .
Проектная отметка следующей точки равна проектной отметке данной точки плюс или минус произведение проектного уклона и горизонтальное проложение линии между этими точками. Знак плюс берут в случае, если проектная линия идет с подъемом, а знак минус, если она имеет спуск.
| № варианта | Пикетаж угла поворота | Угол поворота | Проектная отметка пикета 0 | Уклоны проектной линии | |
| 40-49 | ПК1+60 | 36 40 | Но +2,5 (90,911+2,5=93,411) | -0,004 | спуск |
![]()
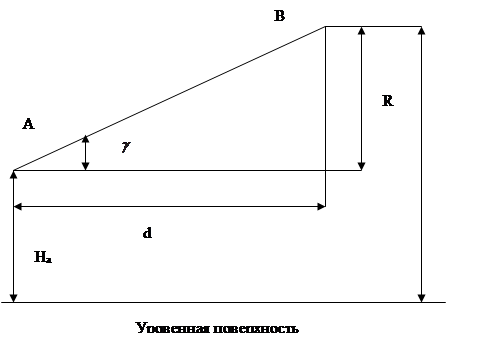
Рис. Вычисление отметок проектной линии
В основу выбора уклонов отдельных участков проектной линии и ее начальной отметки должны быть положены следующие соображения:
1) проектная линия должна быть проведена так, чтобы объем земляных работ был минимальным;
2) количество земляных работ по выемкам и по насыпям должно быть по возможности одинаковым, чтобы землю из выемок можно было использовать для насыпей;
3) уклоны, выбранные для проектной линии, должны быть в пределах величин, рекомендуемых техническими условиями для данного сооружения.
В дано работе уклоны проектной линии и начальная отметка намечаются по заданию.
Заданные уклоны проектной линии выписывают на профиле на графу «уклоны проектной линии». В этой графе число, стоящее над чертой показывает длину участка, на котором проектная линия проходит указанным уклоном. Наклон черты, разделяющий эти два числа, указывает на подъем или спуск проектной линии на данном участке.
Проектные отметки пикетных и плюсовых точек вычислены следующим образом:
НПК1+68 =НПК0 - i * d .= 93,411-(- 0,004*68)=93,411+0,2720=93,683 м,
НПК1 =93,411- (- 0,004*100)=93,811 м,
НПК2 =93,811- (-0,004*100)=94,211 м,
НПК3 =94,211-(-0,004*100)=94,611 м.
Вычисленные таким образом отметки подписывают на профиле в графе «Проектные отметки» против соответствующих им точек.
Отметки проектной линии откладывают от условного горизонта в принятом масштабе так же, как и отметки земли. Для окончательного проведения проектной линии нет необходимости откладывать все подписанные на профиле отметки, достаточно отложить только те
29-04-2015, 00:33
