На сьому добу - ![]()
Таким чином, стік здійснювався протягом 7 діб. Цей розподіл можна зобразити за допомогою графіка, який називається гідрографом формування стоку (рис.5).
Цей гідрограф слід рахувати як теоретичний. Він не обліковує руслове регулювання, коли при підніманні рівну частина води йде на заповнення русла, а при зниженні - навпаки - йде на додатковий приток води з русла. Тому фактичний гідрограф у фазу піднімання має трохи нижчі ординати, а при зниженні - вищі, ніж при будові гідрографа за ізохронами. Фактична максимальна ордината також менша теоретичної і має зсув управо від теоретичної.
Розрахункова робота
Річка Уж
Завдання 1. Характеристика басейну річки та гідрографічної мережі
За звітний період було обстежено від витоку до гирла 6 основних річок області: Тетерів, Случ, Уж, Норинь, Ірша, Гнилоп’ять, а також гирло річки Гуйва, три річки в прикордонних з Київською областю створах: р. Кам’янка, р. Ірпінь та р. Роставиця (басейн р. Рось), і р. Уборть яка є транскордонною між Україною та республікою Білорусь.
Відбір проб здійснюється згідно "Програми моніторингу поверхневих вод суші", розробленої Держуправлінням екології та природних ресурсів в Житомирській області. "Програма..." нараховує 18 пунктів, 23 створи на 11 річках з щоквартальним відбором проб в кожному створі (94 проби). Відібрано по "Програмі моніторингу" 94 проб.
Під час інспекційних перевірок діяльності об"єктів-забруднювачів було перевірено також 30 малих річок (Добринка, Глибочок, Бистріївка, Пустоха, Лісна, Лемня, Настя, Церем, Іршиця, Кам’янка, Чорна Руда, Мика, Тетерівка, Лозниця, Смолка, Хомора, Повчанка, Крошенка, Ужиця, Кропивнянка, Руда, П’яток, Постол, Мурованка, Конявка, Кремна, Унава, Білка, Рихта, Очеретян-ка), 27 кар’єрів, 61 ставок, 9 меліоративних каналів, 6 струмків, 2 свердловини, 3 болота, 1 канава, 2 водосховища, 12 криниць.
Річка Уж.
Річка протікає по території трьох районів: Ємільчинський, Коростенський, і Народицький. Права притока річки Дніпро, протяжність річки в межах області 162 км.
Від витоку в Ємільчинському районі і до міста Коростеня порівняно з2004 роком показники якості води майже не змінились. Відмічається перевищення норм ГДК по залізу загальному в 10,7 рази, при нормі 0,1 мг/дм3 середні значення становлять 1,07 мг/дм3, і фосфатах в 1,6 раз, при нормі 0,17 - фактично - 0,27 мг/дм3.
Нижче міста Коростеня, порівняно з 2004 роком, спостерігається збільшення вмісту нітритів з 0,16 до 0,27 мг/дм3 та заліза загального з 0,68 до 1,16 мг/дм3. Вміст же сольового амонію значно зменшився - з 2,42 мг/дм3 в 2004 до 0,75 мг/дм3 в 2006році. Перевищення норм ГДК відмічається по нітритах в 3,4 рази - 0,27 мг/дм3 при нормі 0,08 мг/дм3, фосфатах в 2,5 рази - 0,43 мг/дм3 при нормі 0,17 мг/дм3 і залізу загальному в 11,6 рази - 1,16 мг/дм3 при нормі 0,1 мг/дм3. Підвищений вміст марганцю спостерігається як у верхньому так і у нижньому створах. Марганець і залізо загальне у річці Уж є природного, а не техногенного походження і не пов’язане з діяльністю людини.
Визначення норми річного стоку при наявності достатньої кількості даних спостережень
Завдання 1. Характеристика басейну річки та гідрографічної мережі
Наводиться гідрографічна характеристика басейну річки.
Довжина lгол головної річки Уж становить 145 км, довжина р. Норин - 75 км, р. Кам'янка - 39 км. Річки Норин і Кам'янка є притоками першого порядку. Площа водозбірного басейну становить 5930 км2 . Коефіцієнт звивистості kзв визначаємо за формулою:
![]()
Довжина водозбірного басейну L становить 27 км. За формулою визначаємо середню ширину басейну:
![]() км
км
Розраховуємо протяжність річкової системи:
145+39+75=259 км
Коефіцієнт щільності рікової мережі d розраховується за формулою:
d = 259/5039=0,05 км/км2 .
Коефіцієнт нерівномірності розвитку річкової мережі kнер розраховується за формулою:
![]()
Визначити середнє багаторічне значення (норму) річного стоку при наявності даних спостережень.
Дано: середні річні витрати води р. Уж за період 1967-2000 рр. (всього за 34 роки).
Розв’язок: розрахунки статистичних параметрів річного стоку проводимо у вигляді таблиці.
У гр.4 значення річного стоку розташовуємо у порядку зменшення.
Таблиця
| № | Роки | Qi , м3 /с | Qi , м3 /с у ранжованому ряді | ki =Qi /Q0 | ki -1 | (ki -1) 2 | (ki -1) 3 | lgki | ki *lgki | P= (m/ (n+1)) *100% |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 1 | 1967 | 2,81 | 6,58 | 3,0463 | 2,046 | 4,1873 | 8,5686 | 0,484 | 1,474 | 2,857 |
| 2 | 1968 | 1,92 | 6,34 | 2,935185 | 1,935 | 3,7449 | 7,2472 | 0,468 | 1,373 | 5,714 |
| 3 | 1969 | 2,28 | 5,79 | 2,680556 | 1,681 | 2,8243 | 4,7463 | 0,428 | 1,148 | 8,571 |
| 4 | 1970 | 2,29 | 4,12 | 1,907407 | 0,907 | 0,8234 | 0,7471 | 0,280 | 0,535 | 11,429 |
| 5 | 1971 | 3,25 | 3,73 | 1,726852 | 0,727 | 0,5283 | 0,3840 | 0,237 | 0,410 | 14,286 |
| 6 | 1972 | 1,45 | 3,51 | 1,625 | 0,625 | 0,3906 | 0,2441 | 0,211 | 0,343 | 20 |
| 7 | 1973 | 3,47 | 3,47 | 1,606481 | 0,606 | 0,3678 | 0,2231 | 0, 206 | 0,331 | 22,857 |
| 8 | 1974 | 1,63 | 3,25 | 1,50463 | 0,505 | 0,2547 | 0,1285 | 0,177 | 0,267 | 28,571 |
| 9 | 1975 | 1,65 | 3,11 | 1,439815 | 0,440 | 0, 1934 | 0,0851 | 0,158 | 0,228 | 31,429 |
| 10 | 1976 | 0,41 | 3,06 | 1,416667 | 0,417 | 0,1736 | 0,0723 | 0,151 | 0,214 | 37,143 |
| 11 | 1977 | 3,11 | 3,02 | 1,398148 | 0,398 | 0,1585 | 0,0631 | 0,146 | 0, 204 | 40 |
| 12 | 1978 | 3,73 | 2,81 | 1,300926 | 0,301 | 0,0906 | 0,0273 | 0,114 | 0,149 | 45,714 |
| 13 | 1979 | 6,34 | 2,44 | 1,12963 | 0,130 | 0,0168 | 0,0022 | 0,053 | 0,060 | 48,571 |
| 14 | 1980 | 3,06 | 2,29 | 1,060185 | 0,060 | 0,0036 | 0,0002 | 0,025 | 0,027 | 51,429 |
| 15 | 1981 | 0,7 | 2,28 | 1,055556 | 0,056 | 0,0031 | 0,0002 | 0,023 | 0,025 | 54,286 |
| 16 | 1982 | 0,64 | 2,22 | 1,027778 | 0,028 | 0,0008 | 0,0000 | 0,012 | 0,012 | 57,143 |
| 17 | 1983 | 1,07 | 2,22 | 1,027778 | 0,028 | 0,0008 | 0,0000 | 0,012 | 0,012 | 60 |
| 18 | 1984 | 1,84 | 2,13 | 0,986111 | -0,014 | 0,0002 | 0,0000 | -0,006 | -0,006 | 62,857 |
| 19 | 1985 | 1,53 | 1,97 | 0,912037 | -0,088 | 0,0077 | -0,0007 | -0,040 | -0,036 | 65,714 |
| 20 | 1986 | 5,79 | 1,92 | 0,888889 | -0,111 | 0,0123 | -0,0014 | -0,051 | -0,045 | 68,571 |
| 21 | 1987 | 6,58 | 1,84 | 0,851852 | -0,148 | 0,0219 | -0,0033 | -0,070 | -0,059 | 71,429 |
| 22 | 1988 | 3,51 | 1,75 | 0,810185 | -0, 190 | 0,0360 | -0,0068 | -0,091 | -0,074 | 74,286 |
| 23 | 1989 | 1,41 | 1,65 | 0,763889 | -0,236 | 0,0557 | -0,0132 | -0,117 | -0,089 | 77,143 |
| 24 | 1990 | 1,75 | 1,63 | 0,75463 | -0,245 | 0,0602 | -0,0148 | -0,122 | -0,092 | 80 |
| 25 | 1991 | 1,17 | 1,53 | 0,708333 | -0,292 | 0,0851 | -0,0248 | -0,150 | -0,106 | 82,857 |
| 26 | 1992 | 1,47 | 1,47 | 0,680556 | -0,319 | 0,1020 | -0,0326 | -0,167 | -0,114 | 85,714 |
| 27 | 1993 | 1,39 | 1,45 | 0,671296 | -0,329 | 0,1080 | -0,0355 | -0,173 | -0,116 | 88,571 |
| 28 | 1994 | 2,22 | 1,41 | 0,652778 | -0,347 | 0,1206 | -0,0419 | -0,185 | -0,121 | 91,429 |
| 29 | 1995 | 2,13 | 1,39 | 0,643519 | -0,356 | 0,1271 | -0,0453 | -0, 191 | -0,123 | 94,286 |
| 30 | 1996 | 1,97 | 1,17 | 0,541667 | -0,458 | 0,2101 | -0,0963 | -0,266 | -0,144 | 97,143 |
| 31 | 1997 | 2,44 | 1,07 | 0,49537 | -0,505 | 0,2547 | -0,1285 | -0,305 | -0,151 | 97,43 |
| 32 | 1998 | 2,22 | 0,7 | 0,324074 | -0,676 | 0,4569 | -0,3088 | -0,489 | -0,159 | 98,3 |
| 33 | 1999 | 3,02 | 0,64 | 0,296296 | -0,704 | 0,4952 | -0,3485 | -0,528 | -0,157 | 98,9 |
| 34 | 2000 | 4,12 | 0,41 | 0,189815 | -0,810 | 0,6564 | -0,5318 | -0,722 | -0,137 | 99,3 |
| Сума | 84,37 | 84,37 | 39,06 | 0,05 | 16,572 | 20,9053 |
-0,488 | 5,079 |
||
Середню багаторічну величину стоку розраховуємо за формулою:
 м3
/с.
м3
/с.
Перевірка розрахунків - сума модульних коефіцієнтів дорівнює кількості років спостережень: Σki =39,06; Σ (ki -1) =0 (допустима нев’язка - 0,05).
Виразити отриману у вигляді середньої багаторічної витрати води норму стоку через інші характеристики стоку: об’єму, модуль, шар та коефіцієнт стоку.
Дано: норма річного стоку р. Уж Q0 =2,5 м3 /с, площа водозбору F=5930 км2 , середньо багаторічна норма річних опадів х0 =20167,8/34=593,2 мм.
Розв'язок: норму стоку виражаємо у інших одиницях стоку за формулами:
W=Q0 *T=2,5*31,56*106 =78,9 млн. м3 (у році 31,56*106 с),
M=Q0 /F*103 =2,5/5930*103 =0,4 л/ (с*км2 ),
y=h=W/F*103 =78,9/5930*103 =13,31 мм
Коефіцієнт стоку розраховуємо за формулою:
α=h/x0 =13,31/593,2=0,2.
Визначити коефіцієнт мінливості (варіації) річного стоку.
Дано: дані табл. .
Розв'язок:
За методом найбільшої правдоподібності коефіцієнт варіації розраховуємо залежно від статистик λ2 та λ3 :
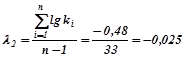
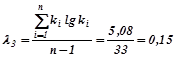 .
.
За номограмою знаходимо:
СV =0,4; СS =2СV =2*0,4=0,8.
За методом моментів коефіцієнт варіації обчислюємо за формулою:
![]() .
.
Визначити відносні середні квадратичні похибки норми стоку і коефіцієнта варіації.
Дано: СV =0,7.
Розв'язок: величину відносної середньоквадратичної похибки σQ0 розраховуємо за формулою:
![]()
Величину відносної середньоквадратичної похибки коефіцієнта варіації δСV визначаємо за формулою:
![]() %
%
![]() %
%
Завдання 3. Побудова кривих забезпеченості річного стоку
Забезпеченістю гідрологічної характеристики називають імовірність перевищення розглядуваного значення цієї характеристики над усіма можливими її значеннями. Наприклад, якщо середньорічна витрата води у 20 м3 /с має забезпеченість 80%, то це означає, що у 80 випадках із 100 спостерігатиметься річна витрата, що дорівнюватиме 20 м3 /с або більше.
Криву забезпеченості, побудовану за даними спостережень, називають емпіричною. Для її побудови хронологічний ряд річних витрат води Q1 , Q2 , …, Qn систематизують у ранжований ряд (розташовують у порядку зменшення від найбільшого значення до найменшого) і обчислюють забезпеченість Р кожного члена ряду за формулою
![]()
Де m - порядковий номер члена ранжованого ряду; n - кількість членів ряду, тобто кількість років спостережень.
Отримані значення Р наносять на сітківку ймовірностей (тип сітківки залежить від співвідношення СS /СV ) і проводять плавну усереднюючи криву - емпіричну криву забезпеченості.
Для згладжування (вирівнювання) та екстраполяції (продовження) емпіричних кривих застосовують теоретичні (аналітичні) криві забезпеченості. Як правило, застосовується аналітична крива три параметричного гама-розподілу при будь-якому співвідношенні СS /СV та біноміальна крива розподілу при СS >2СV .
Для побудови аналітичної кривої три параметричного гама-розподілу ординати її знаходять за таблицею залежно від співвідношення СS /СV ; потім за значенням СV виписують модульні коефіцієнти КР% , які відповідають заданій забезпеченості. Для підвищення точності ординат кривої потрібно враховувати соті частки значення СV (з точністю до двох знаків після коми) шляхом інтерполяції між суміжними колонками цифр.
Ординати біноміальної кривої знаходять за виразом:
КР% =ФР% *СV +1,
Де ФР% - нормоване відхилення ординати кривої забезпеченості від середнього значення (при КР% =1), яке знаходять за таблицею.
Побудувати емпіричну криву забезпеченості річного стоку.
Дано: середні річні витрати води Qi р. Уж за період 1967-1991 рр.
Розв'язок: для розрахунку забезпеченості Р значення річного стоку Qi систематизує у ранжований ряд - розташовуємо у порядку зменшення. Координати емпіричної кривої забезпеченості (Р) обчислюємо за формулою:
![]()
Результати обчислень наведено у таблиці, гр. .11. за цими даними на сітківку ймовірностей наносимо точки емпіричної кривої. По вісі абсцис відкладаємо забезпеченість (масштаб: 1 см - 5%), по вісі ординат - КР% . Для спрощення графік будуємо на міліметровому папері.
Побудувати теоретичну криву три параметричного гама-розподіу забезпеченості річного стоку.
Дано: коефіцієнт варіації СV =0,7.
Розв'язок: координати теоретичних кривих три параметричного гама розподілу визначаємо за додатком для коефіцієнта асиметрії СS =1,5СV , СS =2СV , СS =2,5СV . Записуємо їх у таблицю.
Отримані координати теоретичних кривих наносимо на сітківку ймовірностей. Спів ставляючи побудовані теоретичні криві з емпіричною кривою забезпеченості встановлюємо, що крива три параметричного гама розподілу при СS =2,5СV найкраще узгоджується з емпіричною, тому її приймаємо за розрахункову.
Таблиця
Координати кривої забезпеченості три параметричного гама-розподілу середньорічних витрат води р. Тетерів
| Забезпеченість | |||||||||||
| Р% | 0,1 | 1 | 5 | 10 | 25 | 50 | 75 | 80 | 95 | 97 | 99 |
| Ординати кривої | |||||||||||
| СS =1,5СV | |||||||||||
| КР% | 3,02 | 2,42 | 1,92 | 1,68 | 1,33 | 0,934 | 0,630 | 0,562 | 0,305 | 0,247 | 0,160 |
| СS =2СV | |||||||||||
| КР% | 3,27 | 2,51 | 1,94 | 1,67 | 1,28 | 0,918 | 0,634 | 0,574 | 0,342 | 0,288 | 0, 206 |
| СS =2,5СV | |||||||||||
| КР% | 3,51 | 2,59 | 1,95 | 1,66 | 1,33 | 0,906 | 0,640 | 0,585 | 0,373 | 0,325 | 0,248 |
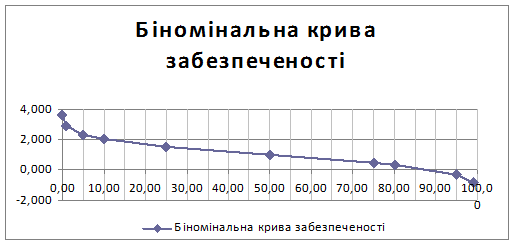
Побудувати біноміальну криву розподілу забезпеченості річного стоку.
Дано: коефіцієнт варіації СV =0,7 коефіцієнт асиметрії СS =2СV =0,8.
Розв'язок: координати біноміальної кривої розподілу знаходимо за виразом КР% =ФР% *СV +1. Розрахунок проводимо у такому порядку: за таблицею додатку 3 знаходимо нормоване відхилення ординати кривої забезпеченості ФР% від середнього значення залежно від СS і обчислюємо значення КР% . результати розрахунків зводимо у таблицю.
Таблиця
Координати біноміальної кривої забезпеченості річного стоку р. Тетерів
29-04-2015, 00:36
