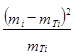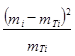0,9
6,385729
7
4,2
0,0001
8
3,9
0,223729
8
4,3
0,0081
9
4,2
0,597529
9
4,4
0,0361
10
4,1
0,452929
11
4,0
0,328329
Среднее значение
3,427
15,401819
Среднее значение
4,21
0,9889
Дисперсия
1,5401819
Дисперсия
0,1236125
20.расчет дисперсии
21. Расчёт среднеквадратичной величины
22. Расчёт коэффициента вариации
23. Определение размаха варьирования
24. Отбраковка непредставительных результатов измерений.
Метод 3 s:
Выборка №1
Значения выборки 1 не выходят за границы критического интервала отбраковки.
Выборка №2
Значения выборки 2 не выходят за границы критического интервала отбраковки.
Метод Башинского:
Выборка №1
Значения выборки 1 выходят за границы критического интервала отбраковки.
Выборка №2
Значения выборки 2 выходят за границы критического интервала отбраковки.
В выборке №1 и №2 по методу Башинского значение выборки вышло за границы критического интервала отбраковки, поэтому 
и 
подлежат отбраковки. Теперь пересчитаем среднюю величину для обоих выборок.
25. Расчёт средней величины
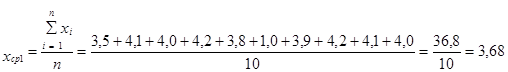
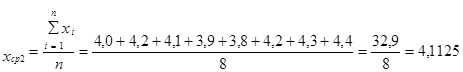
| Выборка №1 |
Выборка №2 |
||||
| 1 |
3,5 |
0,0324 |
1 |
4,0 |
0,01265625 |
| 2 |
4,1 |
0,1764 |
2 |
4,2 |
0,00765625 |
| 3 |
4,0 |
0,1024 |
3 |
4,1 |
0,00015625 |
| 4 |
4,2 |
0,2704 |
4 |
3,9 |
0,04515625 |
| 5 |
3,8 |
0,0144 |
5 |
3,8 |
0,09765625 |
| 6 |
1,0 |
7,1824 |
6 |
4,2 |
0,00765625 |
| 7 |
3,9 |
0,0484 |
7 |
4,3 |
0,03515625 |
| 8 |
4,2 |
0,2704 |
8 |
4,4 |
0,08265625 |
| 9 |
4,1 |
0,1764 |
|||
| 10 |
4,0 |
0,1024 |
|||
| Среднее значение |
3,68 |
8,376 |
Среднее значение |
4,1125 |
0,28875625 |
| Дисперсия |
0,93 |
Дисперсия |
0,04 |
||
26. Расчёт дисперсии
27. Расчёт среднеквадратичной величины.
28. Расчёт коэффициента вариации
29. Определение размаха варьирования.
30. Отбраковка непредставительных результатов измерений.
Метод 3 s:
Выборка №1
Значения выборки 1 не выходят за границы критического интервала отбраковки.
Выборка №2
Значения выборки 2 не выходят за границы критического интервала отбраковки.
Метод Башинского:
Выборка №1
Значения выборки 1 выходят за границы критического интервала отбраковки.
Выборка №2
Значения выборки 2 не выходят за границы критического интервала отбраковки.
В выборке №1 по методу Башинского значение выборки вышло за границы критического интервала отбраковки, поэтому 
подлежит отбраковки. Теперь пересчитаем среднюю величину для выборки №1.
31.Расчёт средней величины.
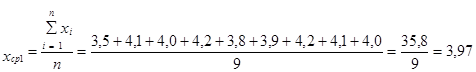
| Выборка №1 |
Выборка №2 |
||||
| 1 |
3,5 |
0,2282716 |
1 |
4,0 |
0,01265625 |
| 2 |
4,1 |
0,0149382 |
2 |
4,2 |
0,00765625 |
| 3 |
4,0 |
0,0004938 |
3 |
4,1 |
0,00015625 |
| 4 |
4,2 |
0,0493827 |
4 |
3,9 |
0,04515625 |
| 5 |
3,8 |
0,0316049 |
5 |
3,8 |
0,09765625 |
| 6 |
3,9 |
0,0060494 |
6 |
4,2 |
0,00765625 |
| 7 |
4,2 |
0,0493827 |
7 |
4,3 |
0,03515625 |
| 8 |
4,1 |
0,0149382 |
8 |
4,4 |
0,08265625 |
| 9 |
4,0 |
0,0004938 |
|||
| Среднее значение |
3,97 |
0,395555 |
Среднее значение |
4,1125 |
0,28875625 |
| Дисперсия |
0,049 |
Дисперсия |
0,04 |
||
32.Расчёт дисперсии.
33. Расчёт среднеквадратичной величины.
34. Расчёт коэффициента вариации.
35. Определение размаха варьирования.
36. Отбраковка непредставительных результатов измерений.
Метод 3 s:
Выборка №1
Метод Башинского:
Выборка №1
Значения выборки 1 выходят за границы критического интервала отбраковки.
В выборке №1 по методу Башинского значение выборки вышло за границы критического интервала отбраковки, поэтому 
подлежит отбраковки. Теперь пересчитаем среднюю величину для выборки №1.
37. Расчёт средней величины.
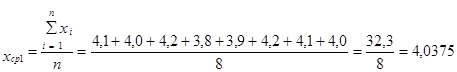
| Выборка №1 |
Выборка №2 |
||||
| 1 |
4,1 |
1 |
4,0 |
0,01265625 |
|
| 2 |
4,0 |
2 |
4,2 |
0,00765625 |
|
| 3 |
4,2 |
3 |
4,1 |
0,00015625 |
|
| 4 |
3,8 |
4 |
3,9 |
0,04515625 |
|
| 5 |
3,9 |
5 |
3,8 |
0,09765625 |
|
| 6 |
4,2 |
6 |
4,2 |
0,00765625 |
|
| 7 |
4,1 |
7 |
4,3 |
0,03515625 |
|
| 8 |
4,0 |
8 |
4,4 |
0,08265625 |
|
| Среднее значение |
4,0375 |
Среднее значение |
4,1125 |
0,28875625 |
|
| Дисперсия |
Дисперсия |
0,04 |
|||
38. Расчёт дисперсии.
39. Расчёт среднеквадратичной величины.
40. Расчёт коэффициента вариации.
41. Определение размаха варьирования.
42. Отбраковка непредставительных результатов измерений.
Метод 3 s:
Выборка №1
Метод Башинского:
Выборка №1
Значения выборки 1 выходят за границы критического интервала отбраковки.
43. Определение предельной относительной ошибки испытаний.
Выборка №1
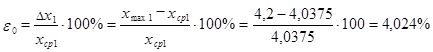
Выборка №2
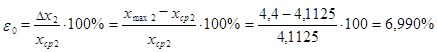
44. Проверка согласуемости экспериментальных данных с нормальным законом распределения при помощи критерия Пирсона.
| № |
Интервал |
Среднее значение |
Частота |
| 1 |
3,8 – 3,9 |
3,85 |
1 |
| 2 |
3,9 – 4,0 |
3,95 |
3 |
| 3 |
4,0 – 4,1 |
4,05 |
2 |
| 4 |
4,1 – 4,2 |
4,15 |
2 |
Выборка №1 Определим количество интервалов:
где 
- размер выборки 1
1. Сравнение с теоретической кривой.
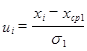- параметр функции 
где
- среднее значение на интервале;
2. Рассчитываем для каждого интервала 
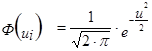- функция плотности вероятности нормально распределения;
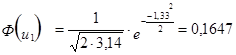
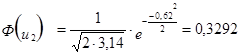
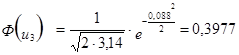
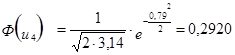
3. Расчёт теоретической частоты.
- теоретическая частота в i-том интервале.
| № |
|
|
|
|
|
|
|
| 1 |
3,85 |
1 |
-1,332 |
0,1647 |
0,9364 |
0,0040 |
0,004 |
| 2 |
3,95 |
3 |
-0,622 |
0,3292 |
1,8717 |
1,2730 |
0,680 |
| 3 |
4,05 |
2 |
0,088 |
0,3977 |
2,2612 |
0,0682 |
0,030 |
| 4 |
4,15 |
2 |
0,799 |
0,2920 |
1,6603 |
0,3397 |
0,204 |
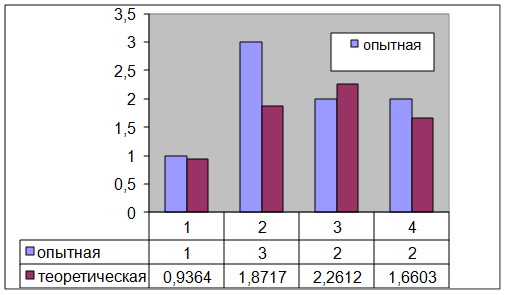
Число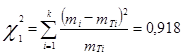 
подчиняется 
- закону Пирсона
- число степеней свободы;
- порог чувствительности;
- вероятность;
Если 
, то данные эксперимента согласуются с нормальным законом распределения, где 
- табличное значение критерия Пирсона.
Если
- данные эксперимента не согласуются с нормальным законом распределения, необходимо дальнейшее проведение опытов. Поскольку вычисленное значение (
) превосходит табличное значение критерия Пирсона, то данные эксперимента не согласуются с нормальным законом распределения.
Выборка №2
Определим количество интервалов:
, где 
- размер выборки 2
| № |
Интервал |
Среднее значение |
Частота |
| 1 |
3,8 – 3,95 |
3,875 |
2 |
| 2 |
3,95 – 4,10 |
4,025 |
2 |
| 3 |
4,10– 4,25 |
4,175 |
3 |
| 4 |
4,25 – 4,4 |
4,325 |
2 |
1. Сравнение с теоретической кривой.
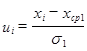- параметр функции 
, где
- среднее значение на интервале;
2. Рассчитываем для каждого интервала 
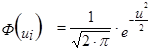- функция плотности вероятности нормально распределения;
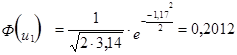
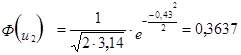
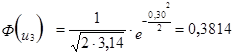
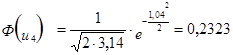
3. Расчёт теоретической частоты.
- теоретическая частота в i-том интервале.
| № |
|
|
|
|
|
|
|
| 1 |
3,88 29-04-2015, 00:58 Разделы сайта |
