Групповой полет летательных аппаратов – алгоритм обработки информации относительного движения.

Движение ЛА, как известно из [4], складывается из поступательного движения его центра масс, определяющего траекторию полета, и вращательного движения вокруг центра масс, определяющего угловое положение ЛА относительно инерциального пространства. При движении ЛА в атмосфере Земли эти две составляющие общего движения взаимосвязаны и должны рассматриваться совместно. Тогда движение отдельного ЛА будет иметь шесть степеней свободы (три поступательные и три вращательные).

В основу математической модели отдельного ЛА положена нелинейная система дифференциальных уравнений, описывающая движение ЛА в пространстве [4].

Как уже отмечалось, задача управления групповым движением связана с необходимостью изучения движения ЛА, находящихся в определенных взаимоотношениях. Поэтому на первый план выступает исследование их относительного движения, математическая модель которого и составляет объект управления.

Движение двух ЛА друг относительно друга представляет собой разность двух абсолютных движений и характеризуется тремя степенями свободы.

Рассмотрим вопрос о внешних возмущениях. Воздействие среды, в которой происходит движение, считаем неконтролируемым и предполагаем, что влияние ее на полет, предшествующий текущему моменту времени , проявляется в реализующемся в этот момент векторе состояния.

Рассматривая движение отдельного ЛА, надо заметить, что действие на объект внешних возмущений (например, ветровых) может привести к заметным искажениям траектории полета. Действие же внешних возмущений на относительное движение ЛА в группе заметного влияния не оказывает, так как для однотипных ЛА при малых рассогласованиях между ними возмущения почти одинаковы и при рассмотрении относительного движения как разности абсолютных движений взаимно исключаются.

Теперь непосредственно перейдем к рассмотрению математической модели относительного движения. Относительное движение ЛА будем рассматривать в общей постановке, когда оба аппарата могут совершать управляемый полет.

Введем некоторые определения. Вектором положения называется вектор, проведенный из начала выбранной СК в точку мгновенного местоположения аппарата. Вектор и скорость его изменения записываются в проекциях на оси выбранной (декартовой или сферической) СК. В первом случае вектор положения определяется тремя его проекциями на оси декартовой СК, во втором  двумя углами и расстоянием r от начала сферической СК до центра масс ЛА. Линией визирования будем называть прямую, соединяющую центры масс ведомого и ведущего ЛА. Вектором относительной дальности назовем вектор, который направлен от ведомого ЛА к ведущему вдоль линии визирования и по величине равен расстоянию между центрами масс этих ЛА. Это расстояние называется относительной дальностью . Скорость ведомого ЛА относительно ведущего называется относительной скоростью: . Плоскостью относительного движения двух ЛА будем называть плоскость, в которой лежат вектора относительной дальности и относительной скорости в данный момент времени. Углами пеленга в работе будем считать два угла (для конкретности назовем их углами места и азимута  рисунок 1), которые определяют ориентацию линии визирования в связанных с ведомым ЛА декартовых СК, вращающихся с угловой скоростью относительно инерциального базиса.

При рассмотрении относительного движения ЛА можно использовать различные СК. Каждая система имеет свои преимущества и недостатки. Выбор ее определяется конкретной задачей. Однако существуют и общие принципы выбора СК, которые обуславливают необходимость или желательность той или иной системы отсчета. Сюда относятся:

простота получаемых уравнений динамики, обеспечивающая простоту анализа задачи и интегрирования этих уравнений;

простота перехода от одной задачи к другой задаче исследуемого класса: математически ее можно выражать условиями, подобными приравниванию к нулю некоторых величин или функций;

простота технической реализации выбранной базовой СК на борту ЛА, определяющая простоту всей системы управления и в особенности ее измерительной части;

простота краевых условий.

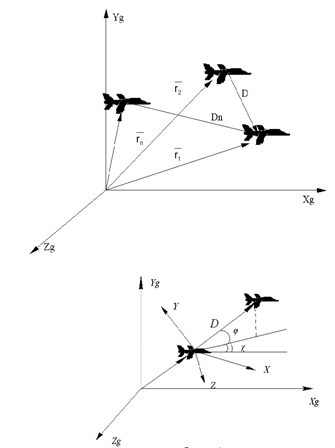
Рисунок 1

С точки 150 которая связана с ведомым ЛА. Начало СК целесообразно совместить с центром масс ведомого ЛА. Причем эта система может быть ориентирована по отношению к связанным осям ЛА различным образом. Во многом это обусловлено тем, что на ведомом ЛА находится измерительная аппаратура, определяющая параметры относительного движения ведомого и ведущего ЛА. Поэтому логично выбрать те варианты ориентации осей и те типы относительных СК, которые используются в качестве базовой системы отсчета при измерении координат относительного движения.

Определенную таким образом СК будем применять для задач управления движением группы ЛА как на прямолинейных участках маршрута, так и на криволинейных. В задаче сбора ЛА в группу целесообразно рассматривать относительное движение в СК, связанной с ведущим ЛА. На этапе сбора ведущий аппарат является пассивным (неманеврирующим), поскольку к его СУ предъявляются требования обеспечения прямолинейного полета.

При выводе уравнений относительного движения двух ЛА в группе будем использовать хорошо известные положения теоретической механики [4]. Используя выше приведенные определения, можно утверждать, что положение аппаратов определяется в каждый момент времени векторами и в земной СК. Следовательно, вектора дальности и относительной скорости запишутся:

,	(1)
.	(2)

Векторное уравнение динамики относительного движения можно представить в виде

,

(3)

где ,  вектора ускорений ведущего и ведомого ЛА соответственно.

Таким образом, относительное движение ЛА в пространстве представляется как движение двух материальных точек О1 и О2, совпадающих с центрами масс двух ЛА: ведущего и ведомого соответственно.

Далее будем описывать относительное движение ЛА в связанной СК ведомого ЛА ОXYZ, перемещающейся относительно инерциальной СК (рисунок 1). В этом случае переход от абсолютных производных векторов к локальным осуществляется по известным формулам:

,	(4)
.	(5)

Здесь точками обозначены производные векторов по времени в связанной СК, вращающейся относительно инерциальной с угловой скоростью . Абсолютное движение ведущего ЛА в связанной СК ведомого ЛА будет определяться выражениями:

,	(6)
,

где ,  векторы ускорений соответственно ведомого ЛА, с которым связана СК, и ведущего ЛА,

,  векторы скорости соответственно ведомого и ведущего ЛА,

 вектор углового ускорения ведомого ЛА.

Будем предполагать, что характер действующих на объект сил нам известен, т.е. известны законы изменения векторов скоростей и ускорений каждого ЛА. Задачу будем видеть в нахождении динамических и кинематических соотношений, определяющих изменение во времени параметров относительного движения.

Кинематические и динамические векторные уравнения относительного движения двух ЛА в связанной СК получим из (6):

,	(7)

Для простоты будем считать, что СК ОXYZ совпадает с горизонтированной СК.

Рассмотрим сначала второе векторное уравнение.

Введем следующие обозначения:

,	(8)
,
.

Из второго векторного уравнения (7) получим динамические уравнения относительного движения двух ЛА в сферической СК, соответствующей горизонтированной:

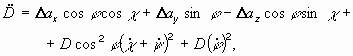	(9)

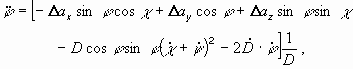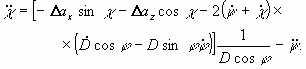Здесь составляющие относительного ускорения , , рассчитываются в горизонтированной СК.

Рассмотрим теперь первое векторное уравнение (7). Введем обозначения:

,	(10)
,
.

Из первого уравнения (7) получим кинематические уравнения относительного движения двух ЛА.

,	(11)
,
.

Чтобы замкнуть систему уравнений относительного движения ЛА, к динамическим и кинематическим соотношениям необходимо добавить уравнения, определяющие величины , , , , , в соответствующих СК.

При исследовании относительного движения ведущего и ведомого ЛА в горизонтированной СК ведомого ЛА можно записать соотношения для , , , , , в таком виде:

где индекс  1 относится к ведущему ЛА, а индекс  2  к ведомому.

3. Синтез алгоритмов обработки информации

Рассмотрим следующий вариант построения алгоритмов управления. Он связан с разработкой алгоритмов оценивания параметров движения ведущего ЛА по результатам измерений относительного движения. Поскольку измерения содержат случайные ошибки, а алгоритм оценки должен быть эффективным в смысле их снижения и снижения влияния этих ошибок на точность получаемых оценок параметров движения ведущего ЛА, то есть алгоритм обработки информации должен обеспечивать фильтрацию ошибок измерений и идентификацию параметров движения ведущего ЛА.

В общем случае алгоритм оценки и идентификации включает в себя блоки первичной и вторичной обработки измерительной информации. Ввиду того, что блок первичной обработки является составной частью измерительной системы и конструктивно с ней совмещен, то алгоритм первичной обработки информации здесь не рассматривается. Основное внимание при дальнейших исследованиях уделяется методам вторичной обработки информации по результатам первичных измерений.

Сначала рассмотрим общие вопросы идентификации моделей динамических систем. Задачу идентификации [5] или, другими словами, задачу оценивания параметров динамической системы можно сформулировать как задачу оценивания параметров модели системы, которая обладает существенными чертами проектируемой системы и представляет знания об этой системе в удобной форме. То есть целью идентификации не является абсолютно точное математическое описание физической реальности, а лишь создание модели, отражающей существенные для дальнейшего применения свойства системы. Положение существенно усложняется, если дополнительно с вектором параметров необходимо оценивать и вектор состояния. Здесь следует обратить внимание на то, что идентификация параметров даже для линейных систем приводит к нелинейным методам оценивания и идентификации.

В настоящее время опубликовано значительное число работ математического характера по оптимальной нелинейной фильтрации . Наиболее общее решение проблемы нелинейной фильтрации получено Р.Л.Стратоновичем в его работах по теории условных марковских процессов [6]. Как показано в работе [6], получение оптимальной нелинейной оценки сводится к решению функционального рекуррентного соотношения для апостериорной плотности вероятности. Основной особенностью задач нелинейной фильтрации является то, что реализация оптимальных алгоритмов обработки информации на современном уровне развития вычислительной техники не представляется возможной из-за сложности решения уравнений для апостериорной плотности вероятности, включающим многомерное интегрирование. Этот факт обусловил появление большого числа работ, посвященных разработке субоптимальных алгоритмов нелинейной фильтрации, основанных на различных аппроксимациях апостериорной плотности вероятности. Разработка субоптимальных алгоритмов диктуется также необходимостью реализации их в системах, работающих в реальном времени и удобством реализации на ЦВМ. С этой точки зрения предпочтительны рекуррентные методы, требующие запоминания на каждом такте сравнительно небольшого числа результатов вычислений.

Рассмотрим теперь конкретно задачу построения алгоритмов CMCН ДПЛА с идентификатором в контуре управления. Имеется несколько вариантов синтеза. В этом случае задача сводится к отысканию расчетных соотношений для параметров , , , , , , , , , , , в предположении, что имеется информация о параметрах относительного движения , , , , , , измеренных с помехами, и параметрах полета ведомого ЛА. Указанные параметры необходимы для реализации алгоритмов СМСН.

Рассмотрим относительное движение двух ЛА в пространстве. В этом случае изменение углов места и азимута, дальности, угловых скоростей линии визирования, радиальной скорости описывается в основной СК системой уравнений вида:

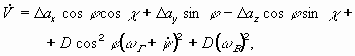	(13)
,

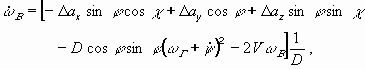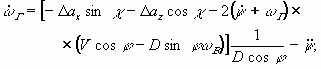где , , .

Эта система может быть положена в основу синтеза алгоритмов нелинейной фильтрации для получения оценок , , , идентификации , , , , , .

Для вычисления оценок параме тров , , , , , , и т.д. необходимо определить математические ожидания этих функций на основе плотности распределения оценок , , , , , . Поскольку этот путь связан с громоздкими вычислениями многомерных интегралов, можно использовать более простой, но приближенный способ, согласно которому оценки перечисленных параметров вычисляются по определенным формулам, куда в качестве , , , , , входят их оценки. Используя информацию об этих оценках, можно определить значения относительных скоростей и ускорений в траекторной СК ведущего ЛА, сформировать программные значения.

Таким образом, основная задача состоит в определении оценок , , , , , . Конкретному рассмотрению алгоритмов оценивания и идентификации параметров относительного движения ЛА предпошлем краткое изложение некоторых общих принципов их построения.

Методически исследование по выбору алгоритмов обработки информации в СМСН ДПЛА проводилось по следующей схеме Это, в первую очередь, касалось замены исходной нелинейной модели состояния и наблюдений тем или иным приближением и построение алгоритма оценивания на основе такой аппроксимации. Во-первых, для решения поставленной проблемы используется подход, основанный на дискретной аппроксимации динамической модели относительного движения. Это позволяет наиболее эффективно реализовать алгоритмы нелинейной фильтрации в БЦВМ, в основу которых положены дискретные методы оценивания. Во-вторых, нелинейные уравнения модели и наблюдений раскладываются в ряд Тейлора до членов первого порядка включительно относительно оценки на предыдущем шаге. В-третьих, в качестве математических моделей идентифицируемых параметров системы используются локальные модели, описывающие изменения параметров лишь в узком диапазоне изменения времени. Простейшей локальной моделью изменения параметров является следующая:

,

(14)

где  вектор параметров,  время.

Другая локальная модель изменения параметров может быть представлена в виде:

,	(15)
,

где вектор подлежит оценке наряду с вектором . В дискретном виде эти модели можно записать соответственно как

,

(16)

и

,	(17)
.

В принципе, значение степени полинома можно повысить, но это усложнение приводит ли шь к незначительному увеличению точности оценки.

В введении таких моделей состоит способ расширения вектора состояния, позволяющий получить принципиальное решение задачи


29-04-2015, 01:59