Групповой полет летательных аппаратов – алгоритм обработки информации относительного движения.

Однако здесь возникает ряд проблем вычислительного порядка, связанных с увеличением размерности задачи оценивания, что ведет к значительному увеличению объема вычислений, и как следствие - к неустойчивости машинных алгоритмов.

В таких условиях чрезвычайно важное, если не решающее, значение приобретает исследование возможностей сведения исходной задачи совместной идентификации, имеющей большую размерность, к задачам меньшей размерности, т.е. возможностей декомпозиции задачи оценивания расширенного вектора состояния (сведение ее к задачам меньшей размерности).

Поэтому в данной работе в качестве одного из путей построения алгоритма оценивания в СМСН ДПЛА предлагается сначала провести идентификацию параметров , , и оценить параметры , , , a затем, уже с учетом этой информации, осуществить идентификацию параметров , , . В свете этих предложений идентификацию параметров целесообразно осуществлять в два этапа. Таким образом, идея этого метода интересна, так как позволяет существенно упростить алгоритмы обработки информации СМСН ДПЛА. Следуя намеченной схеме, решение задач и нелинейной фильтрации при поиске оценок параметров относительного дв ижения ЛА ищется с помощью модифи цированного нелинейного фильтра.

При решении практических задач идентификации возникает проблема обеспечения устойчивости процессов обработки информации. В некоторых случаях реальные ошибки оценивания могут во много раз превосходить расчетные значения, характеризуемые матрицей ковариации ошибок оценивания. Наиболее часто встречающимся источником расходимости являются неточности моделей состояния и наблюдения, неточность задания характеристик шумов и т.д. Так как синтез алгоритмов обычно проводится в условиях априорной неопределенности, то для ее преодоления используют различные адаптивные алгоритмы.

В данной работе с целью устранения в определенных пределах незнания о характеристиках шумов измерений используется идея J-адаптивного фильтра . Такое название он получил по первой букве фамилии автора “J” предложивший алгоритм J-адаптивного фильтра для дискретных систем в работе [7].

В работе [7] J-адаптивный фильтр использован для оценивания параметров движения баллистического объекта: положения и скорости, а также для оценивания вектора аэродинамических параметров (коэффициентов лобового сопротивления и под ъемной силы) или составляющих вектора немоделируемых ускорений по осям декартовой СК. Как указано в этой работе, J- адаптивный фильтр идентифицирует 99% немоделируемых ускорений.

Пусть динамика системы описывается следующим нелинейным уравнением:

(18)

В дискретной форме это уравнение (с точностью до членов второго порядка) будет иметь вид [7] :

,

(19)

где  вектор состояния размерности ,  непрерывная векторная функция, которая по крайней мере дважды дифференцируема по своим аргументам,

,

(20)

матрица Якоби вектор-функции , a отражает погрешность дискретизации и неопределенности моделирования в уравнении динамики. Предполагается, что является белой гауссовской последовательностью с нулевым средним и матрицей ковариации :

,	(21)

где  дельта-функция Кронекера.

Начальное значение вектора состояния принимается гауссовской случа йной переменной с известными средним значением и матрицей ковариации вида:

(22)

Процесс измерения описывается уравнением:

,	(23)
,

где  вектор погрешностей измерений типа белой последовательности с нулевым средним и матрицей ковариации ,  вектор размерности ,  непрерывная векторная функция, дважды дифференцируемая по своим аргументам.

Тогда обобщенный калмановский фильтр описывается следующими уравне ниями:

,	(24)
,	(25)

где  весовая матрица (матрица коэффициентов усиления фильтра).

Уравнения экстраполяции матрицы ковариации:

,	(26)
.

Уравнения коррекции матрицы ковариации:

,	(27)
.

Далее на основе [8] рассмотрим метод получения J-адаптивного нелинейного фильтра .

Предполагается, что в уравнения состояния и измерений входят одни и те же определенные параметры, величины которых известны неточно. Такие параметры можно представить как случайны е переменн ые с заранее известной статистикой , При этом предполагается, что , , , некоррелированы, и матрица ковариации остается неизменной на всем временном интервале процесса оценивания.

При синтезе фильтра в вектор состояния включается вектор . Вводя для вектора параметров уравнения вида

,

(28)

можно получить расширенную систему уравнений с вектором состояния:

,

(29)

и уравнениями измерений:

.

(30)

В этом случае динамические уравнения расширенной системы запишутся в виде

,	(31)
.

Применяя к этой системе нелинейный фильтр можно получить оценки как вектора , так и вектора .

Далее, используя метод изложенный в работе [9] , легко получить уравнения J- адаптивного фильтра. Уравнения J-адаптивного фильтра получаются [9] с помощью расширения вектора состояния путем присоединения переменной , записи расширенного фильтра в виде отдельных уравнений и отбрасывания уравнений для ковариационной матрицы .

В соответствии с этим методом матрица ковариации ошибок оценивания представляется в виде:

,

(32)

где

,	(33)
.

Матрицу можно представить в виде

, где	(34)
, ,

,	(35)

где

,	(36)
,

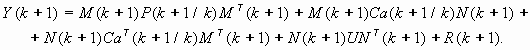Окончательный вид уравнений J-адаптивного фильтра будет следующий:

,	(37)
,
,
,
,
.

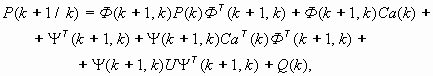Заключение

В данной работе решена задача оценки параметров относительного движения ЛА в групповом полете. Точное определение параметров , , , и особенно , , , необходимо для синтеза алгоритма управления полетом ЛА в группе.

Задача была рассмотрена при полном составе измерений параметров относительного движения ЛА: углах визирования, угловой скорости линии визирования, дальности и скорости изменения дальности.

Ключевым вопросом в решении этой задачи стала разработка математической модели относительного движения ЛА.

Ввиду того, что измерения содержат случайные ошибки. алгоритм оценивания должен обеспечивать снижение ошибок и снижение их влияние точность оценки, а следовательно и на качество управления строем БЛА. Следовательно, в алгоритме было необходимо провести фильтрацию ошибок измерений.

Эта задача была решена посредством применения J-адаптивного фильтра.

Список литературы

Терентьев В.М. Разработка и исследование алгоритмов управления и обработки информации для СМСН БЛА. Доклад на школе-семинаре ЦАГИ по проблемам управления ЛА г. Жуковский 25.02-2.03 1991 г.

Тарасов В.Г. Межсамолетная навигация.  М.: Машиностроение, 1980.  184 с.

Степанов О.А. Применение теории нелинейной фильтрации в задачах обработки навигационной информации. М. ЦНИИ "Электроприбор", 2000.

Горбатенко С.А., Макашов Э.М. и др. Механика полетов. Инженерный справочник. М.: Машиностроение, 1969, 420 с.

Эйкхоф П. Основы идентификации систем управления. М.: Мир, 1975.

Стратонович Р.Л. Условные марковские процессы и их применение к теории оптимального управления. М.: Издательство МГУ, 1966.

Вопросы управления космическими аппаратами. М.:Мир, 1975.

Jazwinski A.H., Stochastic processes and filtering theory, NY.: Academic Press, 1970.

Jazwinski A.H. Nonlinear and adaptive estimation in reentry, AIAA Paper No. 72-874.