Ðèñ. A
Пример 4. Подбрасывается три игральных кубика, подсчитываются суммы очков, выпавших на них. Сколькими способами можно получить в сумме 5 очков; 6 очков?
Решение. Получить в сумме 5 очков можно шестью способами: (1; 1; 3)[4] , (1; 3; 1), (3; 1; 1), (1; 2; 2), (2; 1; 2), (2; 2; 1). Получить в сумме 6 очков можно десятью способами (1; 1; 4), (1; 4; 1), (4; 1; 1), (1; 2; 3), (1; 3; 2), (2; 1; 3), (2; 3; 1), (3; 1; 2), (3; 2; 1), (2; 2; 2).
I. 3. Классическое определение вероятности
Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных исходов опыта, в котором может появиться это событие. Вероятность события A обозначают через P(A) (здесь P — первая буква французского слова probabilite — вероятность):
,
ãäå m — число элементарных исходов, благоприятствующих событию A; n — число всех равновозможных элементарных исходов опыта, образующих полную группу событий.
Это определение вероятности называют классическим. Оно возникло на начальном этапе развития теории вероятностей.
Пример 5. В урне 10 одинаковых по размерам и весу шаров, из которых 4 красных и 6 голубых. Из урны извлекается 1 шар. Какова вероятность того, что извлеченный шар окажется голубым?
Решение. Событие “извлеченный шар оказался голубым” обозначим буквой A. Данное испытание имеет 10 равновозможных элементарных исходов, из которых 6 благоприятствуют событию A. В соответствии с формулой получаем
.
Пример 6. Все натуральные числа от 1 до 30 записаны на одинаковых карточках и помещены в урну. После тщательного перемешивания из урны извлекается одна карточка. Какова вероятность того, что число на взятой карточке окажется делящимся на 5?
Решение. Обозначим через A событие “число на взятой карточке кратно 5”. В данном испытании имеется 30 равновозможных элементарных исходов, из которых событию A благоприятствуют 6 исходов (числа 5, 10, 15, 20, 25, 30). Следовательно,
.
Пример 7. Какова вероятность того, что в наудачу выбранном двузначном числе цифры одинаковы?
Решение. Двузначными числами являются числа от 10 до 99; всего таких чисел 90. Одинаковые цифры имеют 9 чисел (11, 22, 33, 44, 55, 66, 77, 88, 99). В данном случае m = 9, n = 90:
,
где A — событие “число с одинаковыми цифрами”.
Пример 8. Подбрасывается два игральных кубика, отмечается число очков на верхней грани каждого кубика. Найти вероятность того, что на обоих кубиках выпало одинаковое число очков.
Решение. Обозначим это событие буквой A. Событию A благоприятствуют 6 элементарных исходов: (1; 1), (2; 2), (3; 3), (4; 4), (5; 5), (6; 6). Всего равновозможных элементарных исходов, образующих полную группу событий, в данном случае n = 62 = 36 (см. табл. 1). Значит, искомая вероятность
.
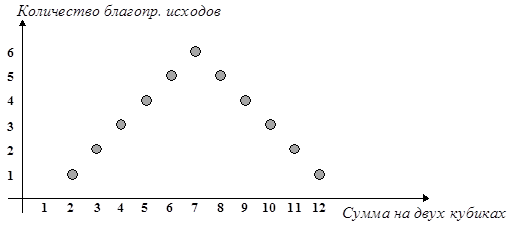
Пример 9. Подбрасываются два игральных кубика, подсчитывается сумма очков на верхних гранях. Что вероятнее — получить в сумме 7 или 8?
Решение. Обозначим события: A — “выпало 7 очков”, B — “выпало 8 очков”. Событию A благоприятствуют 6 элементарных исходов, а событию B — 5 исходов (см. табл. 1, рис. 1). Всех равновозможных элементарных исходов — 36, что видно из той же таблицы. Значит:
, 
.
Итак, 
, т. е. получить в сумме 7 очков — более вероятное событие, чем получить в сумме 8 очков [14, 98].
Задача 1[5] . В урне лежат 5 красных, 12 белых и 9 синих шаров. Найти вероятность того, что: а) вынут белый шар; б) вынут красный шар; в) вынут синий шар; г) вынут цветной шар.
Обсуждение. В задаче имеется 5 + 12 + 9 = 26 равновозможных исходов. Поэтому вероятности равны:
а) 
; б) 
; в) 
.
На случае г) остановимся подробнее. Наверное, цветным шаром можно назвать красный или синий шар. Вынуть цветной шар можно одним из 5 + 9 = 14 способов. Таким образом, цветной шар можно достать 
способами.
Задача 2 (двойное испытание). В урне 3 черных и 4 белых шара. Вы вынимаете один из них, кладете обратно, перемешиваете и вынимаете другой. Возможно одно из трех: 1) оба шара черные, 2) оба шара белые, 3) шары различных цветов. Каковы вероятности этих событий?
Обсуждение. Условно черным шарам дадим номера 1, 2, 3; белым — 4, 5, 6, 7. Пары букв показывают цвет двух вынутых шаров (левая буква относится к первому выниманию, правая — ко второму). Составим таблицу.
Òàáë. B
| 1(ч) |
2(ч) |
3(ч) |
4(б) |
5(б) |
6(б) |
7(б) |
|
| 1(ч) |
чч |
чч |
чч |
чб |
чб |
чб |
чб |
| 2(ч) |
чч |
чч |
чч |
чб |
чб |
чб |
чб |
| 3(ч) |
чч |
чч |
чч |
чб |
чб |
чб |
чб |
| 4(б) |
бч |
бч |
бч |
бб |
бб |
бб |
бб |
| 5(б) |
бч |
бч |
бч |
бб |
бб |
бб |
бб |
| 6(б) |
бч |
бч |
бч |
бб |
бб |
бб |
бб |
| 7(б) |
бч |
бч |
бч |
бб |
бб |
бб |
бб |
Нетрудно подсчитать, что равновозможных исходов 49. Вероятность появления двух черных шаров равна 
, двух белых — 
, шаров разных цветов — 
.
Задача 3. Найдите вероятности того, что при двойном испытании как в предыдущей задаче: а) вынут по крайней мере один черный шар; б) вынут хотя бы один белый шар; в) первым вынут черный шар; г) последним вынут белый шар.
Обсуждение. Для решения воспользуемся таблицей из предыдущей задачи. Вероятности равны: а) 
; б) 
; в) 
; г) 
.
I. 4. О смысле формулы вероятности события
Мы вывели эту формулу с помощью некоторых утверждений. Можно ли утверждать, что мы ее доказали, как доказывают теоремы? Нет, конечно. Мы построили модель реального явления (вынимание шаров из урны). Модель подтверждается фактами и экспериментами. А с математической точки зрения формула есть определение вероятности. И эта формула связывает модель с реальным миром.
Задача 4. Брошены независимо друг от друга две правильные игральные кости. Найти вероятности того, что сумма очков на верхних гранях: а) меньше 9; б) больше 7; в) делится на 3; г) четна.
Обсуждение. При бросании двух костей имеется 36 равновозможных исходов, поскольку имеется 6´6 = 36 пар, в которых каждый элемент — целое число от 1 до 6. Составим таблицу (табл. 3), в которой слева число очков на первой кости, вверху — на второй, а на пересечении строки и столбца стоит их сумма.
Òàáë. C
| 1 |
2 |
3 |
4 |
5 |
6 |
|
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 5 |
6 |
7 |
8 |
9 |
10 |
11 |
| 6 |
7 |
8 |
9 |
10 |
11 |
12 |
Непосредственный подсчет показывает: вероятность того, что сумма очков на верхних гранях меньше 9, равна 
; что эта сумма больше 7 — 
; что она делится на 3: 
; наконец, что она четна, 
.
Задача 5. В старинной индейской игре “Тонг” два игрока одновременно показывают друг другу либо один, либо два, либо три пальца на правой руке. Если для каждого игрока равновозможно показать 1, 2 или 3 пальца, то чему равна вероятность того, что общее число показанных пальцев четно? Нечетно? Больше четырех? Меньше двух?
Обсуждение. Составим таблицу, в которой номер строки — число пальцев, показанных первым игроком, номер столбца — число пальцев, показанных вторым игроком, а на пересечении строки и столбца стоит общее число показанных пальцев, т. е. сумма номеров строки и столбца.
Òàáë. D
| 1 |
2 |
3 |
|
| 1 |
2 |
3 |
4 |
| 2 |
3 |
4 |
5 |
| 3 |
4 |
5 |
6 |
Всего имеется 9 равновозможных исходов, соответствующих девяти элементам таблицы. Общее число показанных пальцев четно в 5 исходах, нечетно — в 4, больше четырех — в 3 исходах, меньше двух — ни в одном. Вероятности равны соответственно 
, 
, 
, 
.
Задача 6. Какова вероятность того, что наудачу выбранное четырехзначное число составлено только из нечетных цифр?
Обсуждение. Всего четырехзначных чисел имеется 9000: они идут в натуральном ряду от 1000 до 9999. Так как нечетных цифр имеется 5, то на каждом из мест (разряды тысяч, сотен, десятков и единиц) может стоять любая из 5 цифр. Всего, таким образом, имеется 5´5´5´5 = 625 четырехзначных чисел, составленных только из нечетных цифр. Значит, искомая вероятность равна 625/9000 = 5/72.
Задача 7. Что вероятнее — выиграть у равносильного противника 3 партии из 4 или 5 партий из 8?
Обсуждение. Прежде всего надо ввести равновозможные исходы. Противники равносильны — это значит, что из большого числа партий примерно половина кончается победой первого, а половина — второго. Мы считаем, кроме того, что результаты нескольких партий не влияют на результаты остальных. Это соглашение дает нам возможность установить, что, скажем, в матче из четырех партий все 2´2´2´2 = 16 возможных последовательностей побед и поражений имеют одинаковую вероятность.
Рассмотрим в качестве примера большое число матчей из двух партий. Из n матчей примерно в n/2 в первой партии победит первый игрок. Поскольку результат первой партии не влияет на результат второй, то примерно в половине тех матчей, где первый игрок победил в первой партии, он проиграет во второй, всего примерно в n/2´1/2 = n/4 матчах. Аналогично события “победил в обоих партиях первый игрок”, “победил в первой партии второй игрок, а во второй — первый”, “в обоих партиях победил второй игрок” будут иметь место примерно в n/4 матчах, т. е. вероятности всех этих событий равны 1/4.
В дальнейшем в задачах мы будем сталкиваться со случаями, когда несколько опытов проводятся независимо друг от друга. Как в предыдущем образце, можно показать, что вероятность события “исход первого опыта есть A, а второго — B” равно произведению вероятностей событий “исход первого опыта есть A” и “исход второго опыта есть B”.
Вернемся к задаче. В матче из четырех партий имеется 16 равновероятных исходов — последовательностей побед и поражений первого игрока. Событию “первый игрок победил в 3 партиях” благоприятны 4 исхода, поскольку единственное поражение может стоять на одном из четырех мест. Значит, вероятность выиграть 3 партии из 4-х у равносильного противника равна 1/4.
В матче из 8 партий имеется 28 = 256 равновозможных исходов — последовательностей побед и поражений первого игрока. В скольких из них ровно 5 побед? Другими словами, сколько существует подмножеств из 5 элементов в множестве из 8 элементов? Комбинаторика подсказывает нам, что это есть число сочетаний из 8 элементов по 5 элементов, которое подсчитывается по формуле: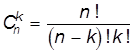 
. Таким образом,
.
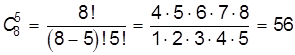Значит вероятность выиграть 5 партий из 8 у равносильного противника равна 56/256 = 7/32, что меньше 1/4 = 8/32 — вероятности выиграть три партии из четырех.
Задача 8. Пусть вы забыли одну цифру нужного вам номера телефона и набираете ее наудачу. Какова вероятность того, что вам придется сделать не более двух звонков?
Обсуждение. Вероятность того, что первый же раз вы наберете правильный номер равна 1/10 , поскольку цифр всего десять; все десять исходов — набор 1, набор 2 и т. д. — равновозможны, а благоприятным является только один из них. Если первый раз забытая цифра была набрана неправильно, то при втором звонке вы будете набирать одну из девяти оставшихся цифр, и вероятность успеха будет равна 1/9. Ровно два звонка будут сделаны с вероятностью 9/10´1/9 = 1/10. Вероятность того, что придется сделать не более двух звонков, равна 1/10 + 1/10 = 0,2.
Задача 9. Бросают три игральные кубика. Что вероятнее: сумма очков на верхних гранях равна 11 или эта сумма равна 12? Каковы вероятности этих событий?[6]
Обсуждение. Прежде всего найдем, сколькими способами можно представить 11 и 12 в виде суммы трех натуральных слагаемых, каждое из которых не превосходит 6. Будем выписывать суммы в порядке возрастания слагаемых. Начнем с 11. Если наименьшее слагаемое — 1, то 11 = 1 + 4 + 6 либо 11 = 1 + 5 + 5. Если 2, то 11 = 2 + 3 + 6 либо 11 = 2 + 4 + 5. Если 3, то 11 = 3 + 4 + 4 либо 11 = 3 + 3 + 5. Этими случаями (6) исчерпываются все представления 11 в виде суммы трех чисел, нанесенных на грани кубиков. Число 12 можно представить шестью способами: 12 = 1 + 5 + 6 = 2 + 4 + 6 = 2 + 5 + 5 = 3 + 3 + 6 = 3 + 4 + 5 = 4 + 4 + 4. Шевелье де Мере заключил отсюда, что 12 в качестве суммы будет встречаться столь же часто, как и 11. Однако результаты многих игр показали, что, вопреки расчетам де Мере, 11 встречается чаще. Именно тогда Мере усомнился в теории вероятностей и обратился к Паскалю за
10-09-2015, 03:50