Полученные таким образом расчеты средней и структурных средних свидетельствуют о том, что наиболее часто в Рязанской области встречаются районы с числом дневных общеобразовательных учреждений равным 23. Однако более половины районов области имеют 26 общеобразовательных учреждений, при среднем количестве общеобразовательных заведений в районах 27.
При изучении явлений и процессов общественной жизни статистика встречается с разнообразной вариацией признаков, характеризующих отдельные единицы совокупности. Величины признаков изменяются под действием различных факторов. Очевидно, чем разнообразнее условия, влияющие на размер данного признака, тем больше его вариация.
При характеристике колеблемости признака применяют систему абсолютных и относительных показателей.
К абсолютным показателям вариации относят:
· размах вариации R = xmax – xmin;
· среднее линейное отклонение 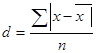
· дисперсия s2
= 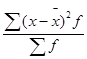
· среднеквадратическое отклонение s =![]() .
.
Эти показатели (кроме дисперсии) измеряются в тех же единицах, что и сам признак: в тоннах, метрах, секундах, рублях. К относительным показателям вариации относятся:
· коэффициент осцилляции Косу
= ![]()
![]()
· Линейный коэффициент вариации Kл..вар
= ![]()
· Коэффициент вариации V = ![]()
Эти показатели выражаются в процентах или коэффициентах.
Наиболее простым способом измерения колеблемости является определение размаха вариации, то есть разности между максимальным и минимальным значениями признака. Величина R показывает, в каких пределах колеблется размер признака, образующего ряд распределения. Показатель R выражается в тех же единицах измерения, что и варианты признака. Но размах вариации, как показатель колеблемости имеет существенный недостаток. Его величина определяется крайними значениями признака, в то время как колеблемость последнего в целом складывается из суммы всех значений. Поэтому размах вариации может в ряде случаев неправильно характеризовать колеблемость признака.
В статистическом анализе вариации имеет большое значение дисперсия (s2 ). Однако ее применение как мера вариации в ряде случаев бывает не совсем удобным, потому что размерность дисперсии равна квадрату размерности изучаемого признака. В таких случаях для измерения вариации признака вычисляют среднеквадратическое отклонение.
Дисперсия и среднеквадратическое отклонение недостаточно полно характеризуют колеблемость признака, так как показывают абсолютный размер отклонений, что затрудняет сравнение изменчивости различных признаков.
Для характеристики колеблемости явлений среднеквадратическое отклонение сопоставляют с его средней величиной и выражают в процентах. такой показатель называют коэффициентом вариации и рассчитывают по формуле:
![]() .
.
По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.
Вычислим показатели вариации, для чего используем данные табл. 5.
Таблица 5. Расчетные значения показателей вариации
| X | f | (x –
|
(x –
|
(x –
|
| 10 | 5 | -17 | 289 | 1445 |
| 20 | 9 | -7 | 49 | 441 |
| 30 | 8 | 3 | 9 | 72 |
| 40 | 5 | 13 | 169 | 845 |
| 50 | 2 | 23 | 529 | 1058 |
| 150 | 29 | x | x | 3861 |
s2
= 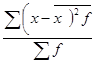 =
= ![]() = 133,1
= 133,1
s = ![]() = 11,5
= 11,5
Коэффициент вариации:
Vs
=![]() * 100% =
* 100% = ![]() * 100% = 42,7%
* 100% = 42,7%
Среднеквадратическое отклонение показывает, что число общеобразовательных учреждений районов Рязанской области отклоняется от среднего размера на 11 единиц.
Значение коэффициента вариации свидетельствует о том, что рассмотренная совокупность количественно неоднородная, так как Vs >33%.
3. Динамика показателей сферы образования в Рязанской области
Процессы и явления общественной жизни, являющиеся предметом изучения статистики, находятся в постоянном движении и изменении.
Ряд цифровых данных в определенной, хронологической последовательности, характеризующие изменения явлений во времени, называются динамическими рядами . Такие ряды строят для выявления и изучения складывающихся закономерностей в развитии явлений экономической, политической и культурной жизни общества.
Правильно построенный динамический ряд состоит из сопоставимых статистических показателей. Для этого необходимо, чтобы состав изучаемой совокупности был один и тот же на всем протяжении ряда, то есть относился к одной и той же территории, к одному и тому же кругу объектов и был рассчитан по одной и той же методологии. Кроме того, данные динамического ряда должны быть выражены в одних и тех же единицах измерения, а промежутки времени между значениями ряда должны быть по возможности одинаковыми.
В зависимости от характера изучаемых величин различают три вида динамических рядов: моментные, интервальные и ряды средних.
Моментными рядами называются статистические ряды, характеризующие размеры изучаемого явления на определенную дату, момент времени.
Интервальными рядами называются статистические ряды, характеризующие размеры изучаемого явления за определенные промежутки времени.
Для общей характеристики какого-либо явления за определенный период рассчитывают средний уровень всех членов динамического ряда . Способы его расчета зависят от вида динамического ряда. Для интервальных рядов средняя рассчитывается по формуле средней арифметической, причем при равных интервалах применяется средняя арифметическая простая, а при неравных – средняя арифметическая взвешенная.
Для нахождения средних значений моментного ряда применяют среднюю хронологическую:
![]() = Ѕ
y
1
+
y
2
+
y
3
+ ….‚Ѕ
yn
= Ѕ
y
1
+
y
2
+
y
3
+ ….‚Ѕ
yn
n-1
Динамические ряды анализируются при помощи таких показателей, как уровень ряда, средний уровень, абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста.
Уровнем ряда называется абсолютная величина каждого члена динамического ряда. Различают начальный, конечный и средний уровни ряда.
Абсолютный прирост ( D y ) характеризует размерувеличения или уменьшения изучаемого явления за определенный период времени. Он определяется как разность между двумя сравниваемыми уровнями ряда по формуле: Dy = Yi - Yi – 1 , или Dy = Yi – Y0, где
Yi – текущий уровень ряда;
Yi – 1 – предыдущий уровень ряда;
Y0 – уровень базисного года. [4, стр. 18]
Если каждый уровень ряда сравнивается с предыдущим, то получают цепные показатели динамики. Если же уровни ряда сравниваются с одним и тем же первоначальным уровнем, то полученные показатели называются базисными.
Темп роста (Тр ) – отношение данного уровня явления к предыдущему или начальному, выраженное в процентах. Темпы роста, вычисленные как отношение данного уровня к предыдущему, называются цепными, а к начальному – базисными и вычисляются по формулам:
цепной Тр = Yi __ * 100%
базисный Тр = Yi __ * 100%
Yi – 1 Y0
Если темпы роста выражены в виде простых отношений, то есть база сравнения принимается за единицу, а не за 100%, то полученные показатели называются коэффициентами роста.
Темпом прироста (Тпр ) называется отношение абсолютного прироста к предыдущему или начальному уровню, выраженное в процентах и рассчитывается по фомулам:
Тпр = D __ * 100 или Тпр = D __ * 100
Yi – 1 Y0
Темп прироста можно рассчитать по данным о темпе роста. Для этого надо от темпа роста отнять 100 или от коэффициента роста 1 (Тпр = Тр – 100%) или (Тпр = Кр – 1), в последнем случае получим коэффициент прироста.
Абсолютное значение одного процента прироста определяется отношением абсолютного прироста к темпу прироста за этот же период:
Расчет этого показателя имеет экономический смысл только на цепной основе.
Среднегодовой абсолютный прирост определяется по цепным абсолютным приростам по формуле:
![]() =
= ![]() или
или ![]() ,
,
где N – число абсолютных приростов.
Среднегодовой темп роста (Тр ) определяется по формуле средней геометрической:
![]() р
=
р
= ![]() или
или ![]() р
=
р
= ![]() ,
,
где К – цепные коэффициенты роста.
По данным о численности педагогических работников государственных общеобразовательных учреждений Рязанской области построим динамический ряд и проведем анализ динамики.
Таблица 6. Численность педагогических работников государственных образовательных учреждений. Их образовательный уровень, (человек)
| Показатели / Годы | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 |
| Учителя дневных общеобразовательных учреждений | 15133 | 14461 | 14262 | 14007 | 13490 | 13003 |
| В том числе с высшим образованием (в% к общему числу) | 80 | 80 | 81 | 82 | 82 | 83 |
| Преподаватель средних специальных учебных заведений | 1252 | 1234 | 1288 | 1249 | 1278 | 1286 |
| В том числе с высшим образованием (в% к общему числу) | 95 | 94 | 87 | 92 | 94 | 94 |
| Преподаватели высших учебных заведений | 1810 | 2087 | 2136 | 2247 | 2245 | 2269 |
В том числе (в% к общему числу) – доктора наук |
11 | 11 | 11 | 11 | 12 | 12 |
| кандидаты наук | 53 | 51 | 55 | 55 | 56 | 56 |
| ИТОГО: | 18195 | 17782 | 17686 | 17503 | 17013 | 16558 |
Таблица 7. Показатели динамики численности педагогических работников Рязанской области
| Годы | Символы | Число педагогических работников (человек) | Абсолютный прирост | Темп роста | Темп прироста | Значение в% прироста | |||
| цепной | базисный | цепной | базисныйый | цепной | базисныйый | ||||
| 2004 | У0 | 18195 | - | - | - | - | - | - | - |
| 2005 | У1 | 17782 | -413 | -413 | 97,7 | 97,7 | -2,3 | -2,3 | 179,6 |
| 2006 | У2 | 17686 | -96 | -509 | 99,5 | 97,2 | -0,5 | -2,8 | 192,0 |
| 2007 | У3 | 17503 | -183 | -692 | 99,0 | 96,2 | -1,0 | -3,8 | 183,0 |
| 2008 | У4 | 17013 | -490 | -1182 | 97,2 | 93,5 | -2,8 | -6,5 | 175,0 |
| 2009 | У5 | 16558 | -455 | -1637 | 97,3 | 91,0 | -2,7 | -9,0 | 168,5 |
| ИТОГО: | 104737 | -1637 | х | х | х | х | х | х | |
В 2009 году численность педагогических работников Рязанской области сократилось на 9,0% по сравнению с 2004 годом, в абсолютном выражении это составляет 1637 человек. Каждый процент абсолютного снижения в 2009 году составил 168 человек. Таким образом многие школы Рязанской области испытывают затруднения с укомплектованием учителями – предметниками.
При изучении в рядах динамики основной тенденции развития явления применяются различные приемы и методы: метод укрупнения периодов, скользящей средней, метод аналитического выравнивания по способу наименьших квадратов. При этом главное – правильно выбрать вид уравнения.
Метод аналитического выравнивания
основан на том, что уровни ряда динамики выражаются в виде функции времени: ![]() t
= f (t).
t
= f (t).
Для выравнивания ряда динамики по прямой используется уравнение: ![]() t
= a + bt
t
= a + bt
Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров а и b:
åУ = na + båt;
åУt = aåt + båt2 ;где:
У – исходные уровни ряда динамики;
n – число членов ряда;
t – показатель времени.
Для упрощения техники расчета параметров уравнения показателям времени (t) придают такие значения, чтобы их сумма была равна нулю, то есть åt = 0.
При условии, что åt = 0, система нормальных уравнений упрощается, приобретая в случае линейной зависимости такой вид:
![]() na = åУ
na = åУ
![]() båt2
= åУt, отсюда:
båt2
= åУt, отсюда:
a = å У ; b = å У t
nåt2.
В практической деятельности может возникнуть необходимость интерполяции или экстраполяции рядов динамики. Самым совершенным при этом является их выравнивание по определенному аналитическому уровню.
Интерполяция – это нахождение отсутствующих промежуточных уровней ряда. Зная уравнение тренда для вычисления теоретических уровней и подставляя в него промежуточные значения ( t) между заданными, можно определить отвечающий им теоретический уровень результативного фактора Уt.
Экстраполяция используется при прогнозировании общественных явлений в будущем с предположением, что выявленная тенденция будет сохраняться и в дальнейшем за пределами исследуемого ряда динамики. При этом значения (t) вне пределов динамического ряда подставляют в уравнение тренда и получают точечное прогнозное значение уровня тренда в будущем.
Общее представление о характере тенденции изменения явления можно получить из графического изображения ряда динамики (рис. 3).
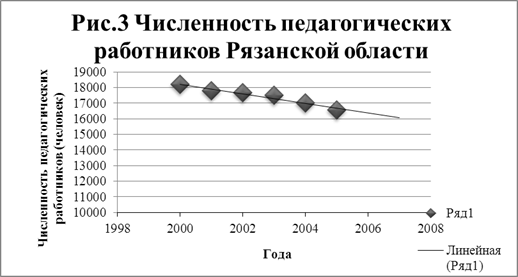
Из графика видно, что фактические данные ряда динамики размещены близко к прямой линии. Тогда выравнивание ряда динамики осуществляется по прямой, которая описывается уравнением тренда в виде функции:
Уt = а + bt, где
а и b – параметры уравнения тренда;
t – порядковый номер периодов времени.
Необходимые данные для определения уравнения тренда приведены в таблице 8.
Таблица 8. Выявление тенденции динамики численности педагогических работников Рязанской области
| Годы | Число педагогических работников (человек) | t | t2 | Уt | Уt = 17456.17 – 236.86 |
| 2004 | 18195 | -3 | 9 | -54585 | 18167 |
| 2005 | 17782 | -2 | 4 | -35564 | 17930 |
| 2006 | 17686 | -1 | 1 | -17686 | 17693 |
| 2007 | 17503 | 1 | 1 | 17503 | 17219 |
| 2008 | 17013 | 2 | 4 | 34026 | 16982 |
| 2009 | 16558 | 3 | 9 | 49674 | 16746 |
| Сумма | 104737 | å t = 0 | 28 | -6632 | 104737 |
а = ![]() = 17456,17
= 17456,17
b = 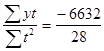 = -236,86
= -236,86
Уравнение тренда ![]()
![]() t
= 17456.17 – 236.86
t
используем для экстраполяции. Прогноз численности педагогических работников представим в таблице 9.
t
= 17456.17 – 236.86
t
используем для экстраполяции. Прогноз численности педагогических работников представим в таблице 9.
Таблица 9. Прогнозные значения численности педагогических работников Рязанской области
| Годы | t | |
| 2010 | 4 | 16509 |
| 2011 | 5 | 16271 |
| 2012 | 6 | 16035 |
Полученные прогнозные значения отразим графически на рисунке 3, построив линию тренда.
4. Индексный анализ образования Рязанской области
Индексами в статистике называются относительные показатели, характеризующие изменение во времени или в пространстве сложных общественных явлений, отдельные элементы которых, непосредственно не поддаются суммированию.
При помощи индексов:
1. определяются средние изменения сложных, непосредственно несоизмеримых совокупностей во времени;
2. оценивается средняя степень выполнения плана совокупности в целом или ее части;
3. устанавливаются средние соотношения сложных явлений в пространстве;
4. определяется роль отдельных факторов в общем изменении сложных явлений во времени или в пространстве и, в частности, изучается влияние структурных сдвигов.
При решении первой задачи – изучение изменения явлений во времени – индексы выступают как показатели динамики, при решении второй – как показатели выполнения плана, третьей – как показатели сравнения, четвертой – как аналитическое средство.
По степени охвата единиц совокупности различают индивидуальные и общие индексы.
Индивидуальные индексы ( i ) – показывают изменение отдельных элементов сложного явления. Они определяются как отношение величин признака в отчетном и базисном периодах.
Период, уровень которого сравнивается, называется отчетным, или текущим периодом, а уровень, с которым производится сравнение, называется базисным.
Индивидуальные индексы выражаются следующими формулами:
индекс физического объема
– iq
= ![]() , где
, где
q1 и q0 – объем продукции в отчетном и базисном периодах;
индекс цен
– ip
= ![]() , где
, где
p1 и p0 – цена единицы продукции в отчетном и базисном периодах;
индекс
себестоимости
– iz
= ![]() , где
, где
z1 и z0 – себестоимость единицы продукции в отчетном и базисном периодах;
индекс прибыли
– im
= ![]() , где
, где
m1 и m0 – прибыль на производство единицы продукции в отчетном и базисном периодах.
Следовательно, индивидуальные индексы представляют собой, по существу, относительные показатели динамики, выполнения плана, сравнения.
Индекс как относительный показатель, выражается в виде коэффициента, когда база сравнения принимается за единицу и, в процентах, когда база сравнения принимается за 100. Если в результате вычислений полученный индекс больше 1 или 100%, то это указывает на рост явления, если же меньше 1 или 100% – на снижение уровня изучаемого явления.
Индивидуальные индексы могут рассчитываться в виде индексного ряда за несколько периодов. При этом существует два способа их расчета: цепной и базисный.
При цепном способе расчета за базу сравнения принимается индексируемая величина смежного прошлого периода. При этом база расчета в ряду постоянно меняется – х0 х1 х2 х3 х4.
При базисном способе расчета за базу принимается неизменная индексируемая величина какого-то одного (обычно начального) периода – ![]()
![]()
![]()
![]() .
.
Между базисными и цепными индексами существует взаимосвязь:
– при перемножении цепных индексов, получается базисный,
– при делении базисного на предыдущий, получается цепной индекс.
В случае однородной совокупности для ее характеристики могут быть использованы индивидуальные индексы, которые не нуждаются в суммировании элементов этой совокупности.
В случае неоднородной совокупности ее элементы не подлежат суммированию в виду разной натуральной сути явления и разных единиц измерения. В этом случае используют общие индексы.
Общие индексы ( I ) показывают соотношение совокупности cложных явлений, состоящей из разнородных, непосредственно несоизмеримых элементов. Их основной задачей является – выявление влияния отдельных факторов на величину сложного явления.
Основной формой общего индекса является агрегатная :
Ip
= ![]() , где
, где
р – индексируемая величина, то есть так как называется индекс (изменяющаяся);
q – соизмеритель.
Различают качественные и количественные формы агрегатных индексов. Количественные можно складывать, а качественные – нет.
Среди агрегатных индексов качественных показателей различают:
– агрегатный индекс цен – Ур
= 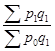 ;
;
– агрегатный индекс себестоимости продукции – Уz
= 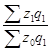 ;
;
– агрегатный индекс производительности труда – Уt
= ![]() .
.
Наиболее типичным общим индексом количественных показателей является индекс физического объема, который записывается в виде формулы: Уq
= 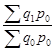 .
.
В экономико-статистическом анализе приходится сравнивать в динамике такие обобщающие показатели качественных характеристик, как средняя цена, средняя себестоимость, средняя производительность труда и другие. Так как на динамику средней влияют не только изменения осредняемого признака, но и изменения состава рассматриваемой совокупности, влияние каждого из этих факторов оценивается посредством общих индексов средних величин. Такие индексы образуют индексную систему, это:
· Средний арифметический индекс получается из агрегатного, если заменить значение индексируемой величины второго из сравниваемых периодов.
Iq
= ![]() ; Iq
=
; Iq
= ![]() ; q1
= iq
q0
; Iq
=
; q1
= iq
q0
; Iq
= ![]() .
.
· Средний гармонический индекс представляет собой среднюю гармоническую из индивидуальных индексов. Индексируемая величина знаменателя заменяется через индивидуальный индекс и индексируемую величину другого периода.
Ip
= 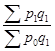 , iq
=
, iq
= ![]() ; P0
=
; P0
= ![]() ; Ip
=
; Ip
= 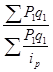 .
.
Различают индексы постоянного и переменного состава.
К индексам постоянного относятся те, у которых соизмеритель и в числителе и в знаменателе одинаковый:
Iq
=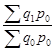 , Ip
=
, Ip
=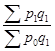 , Iz
=
, Iz
=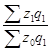 .
.
Относительные величины, характеризующие динамику двух средних показателей для однородной совокупности, в статистике называют индексом переменного состава .
Jp
= 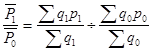 .
.
Рассмотрим следующие данные об оказании платных услуг образования в таблице 10.
Таблица 10. Рынок платных услуг в системе образования Рязанской области
| Вид услуги | Ед. измерения | Средние потребительские цены (руб.) | Объем оказанных услуг(единиц) | P0 q0 | P1 q1 | P0 q1 | ||
| 2005 | 2008 | 2005 | 2008 | |||||
| Детские ясли-сад | 1 день посещения | 10,15 | 21,34 | 10617800 | 8987100 | 107770670 | 191784714 | 91219065 |
| Занятия на курсах иностранных языков | 1 академический час | 39,17 | 58,87 | 482100 | 634150 | 18883857 | 37332410,5 | 24839655,5 |
| Обучение в государственных вузах | 1 семестр | 8331,25 | 15009,42 | 3279 | 6851 | 27318168,75 | 102829536,4 | 102829536,4 |
| х | х | х | Х | 153972695,8 | 331946660,9 | 218888256,9 | ||
Исходя из полученных данных можно сделать вывод:
Ipq
= 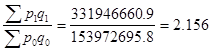 или 215,6%
или 215,6%
Ip
=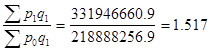 или 151,7%
или 151,7%
Iq
= 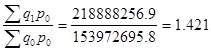 или 142,1%
или 142,1%
Общий объем платных услуг образовательных учреждений Рязанской области
10-09-2015, 14:45
