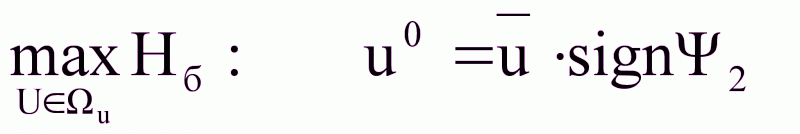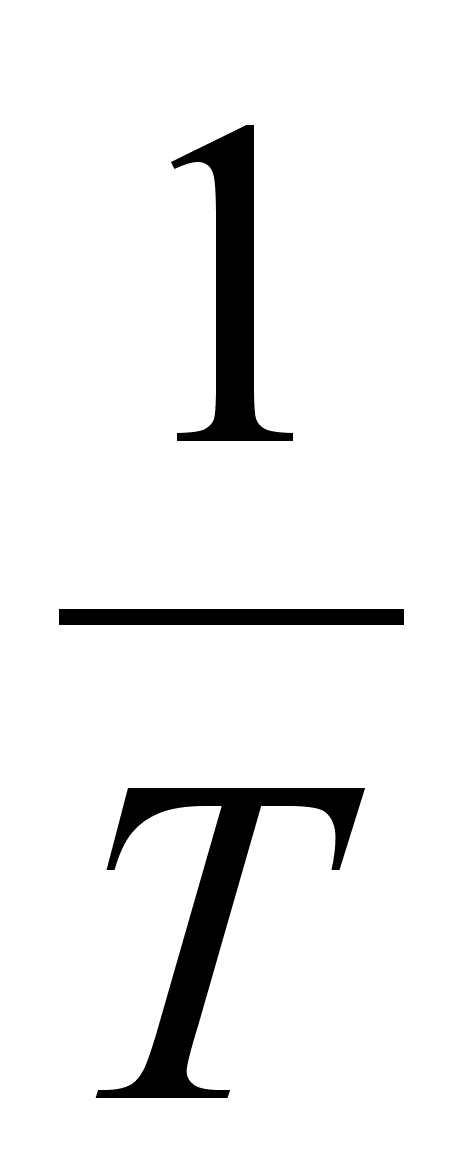
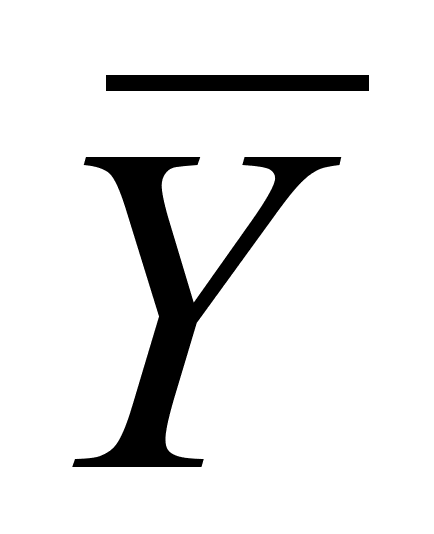
![]()
![]()
![]()
![]()

G
Рис. 1.12. Схема специального фильтра оценки частной производной
T-
постоянная
времени фильтра 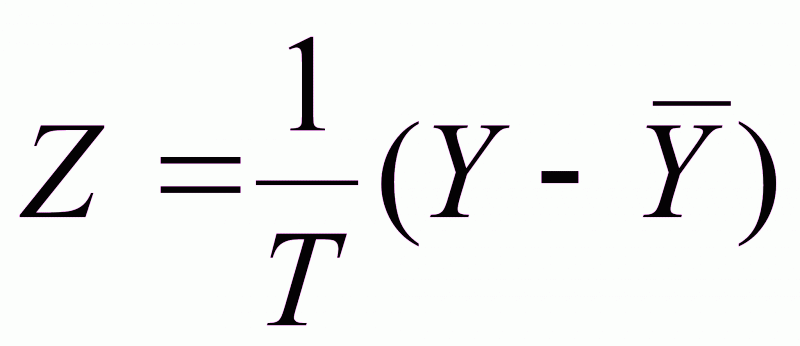
 ;
;
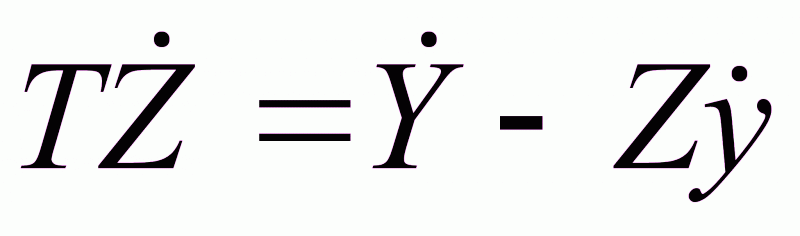 ; (1.20)
; (1.20)
При
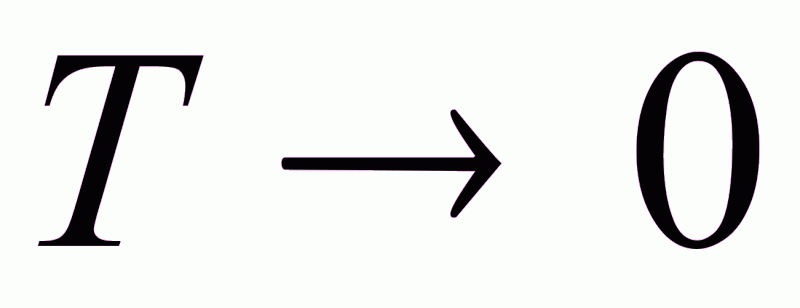 :
:
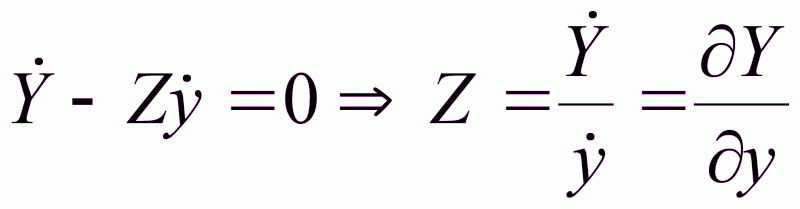 (1.21)
(1.21)
Для оценки полной производной Y используют ДФ – дифференцирующий фильтр, а затем эта оценка полной производной применяется для оценки градиента.
1.5. Организация движения к экстремуму
1.5.1. Системы первого порядка
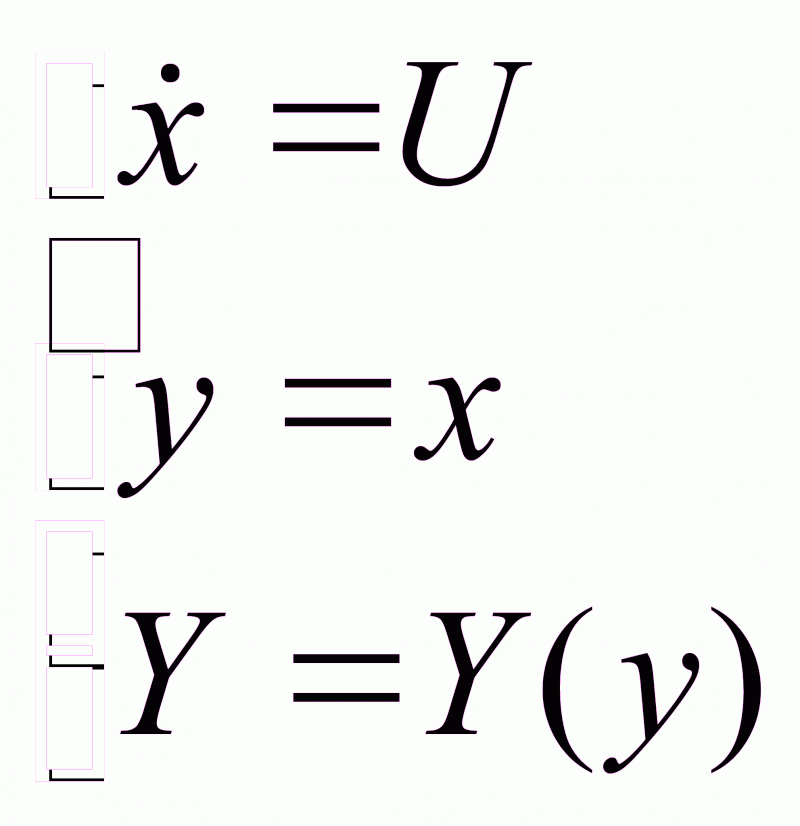 (1.22)
(1.22)
Организуем закон управления пропорционально градиенту:
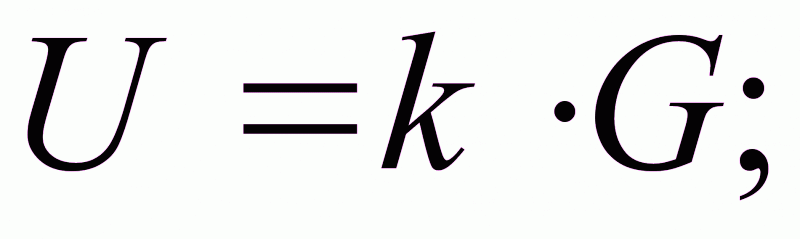
 (1.23)
(1.23)
Запишем уравнение замкнутой системы:
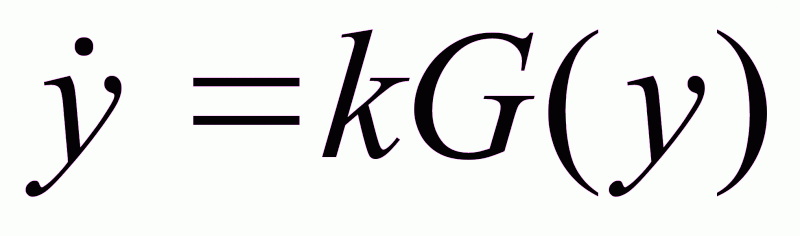 - нелинейное
дифференциальное
уравнение
(1.24)
- нелинейное
дифференциальное
уравнение
(1.24)
Это обычное дифференциальное уравнение, которое можно исследовать методами ТАУ.
Рассмотрим уравнение статики системы:
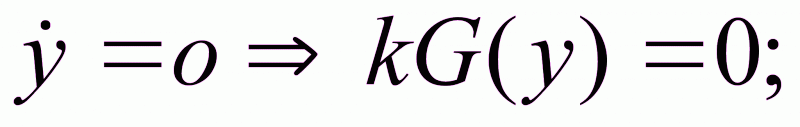 т.к.
т.к.
 ,
то из уравнения
следует, что
,
то из уравнения
следует, что
![]()
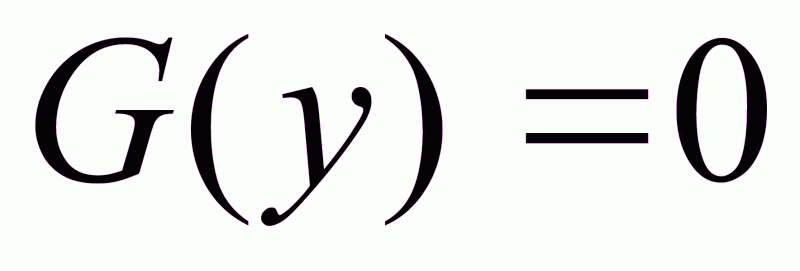 (1.25)
(1.25)
Если с помощью коэффициента усиления k обеспечить устойчивость замкнутой системы, то автоматически в статике мы придём в точку экстремума. В некоторых случаях с помощью коэффициента k можно кроме устойчивости обеспечить определённую длительность переходного процесса в замкнутой системе, т.е. обеспечить заданное время выхода на экстремум.
Пример:

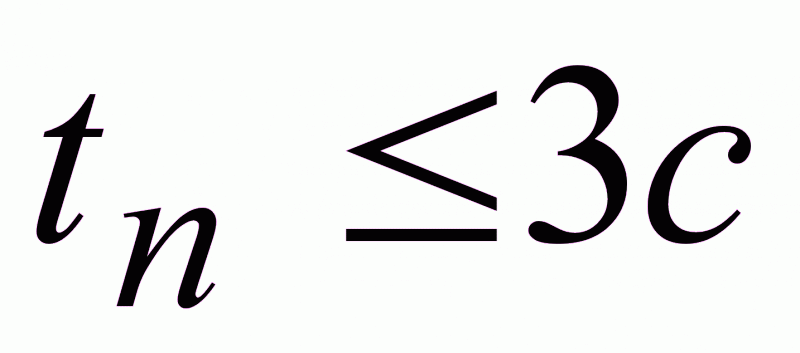 ;
;  ;
;
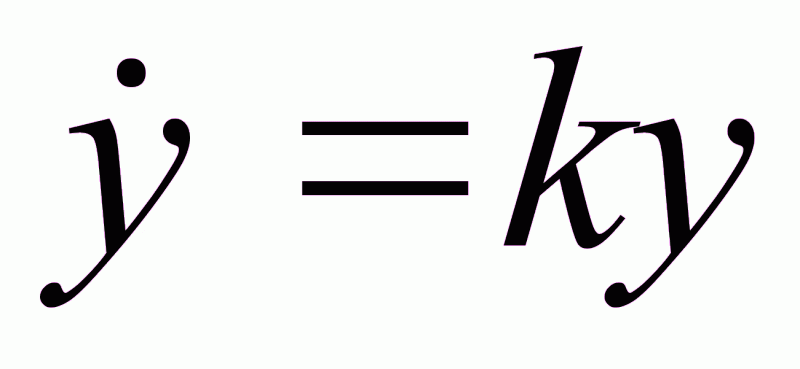 ;
;
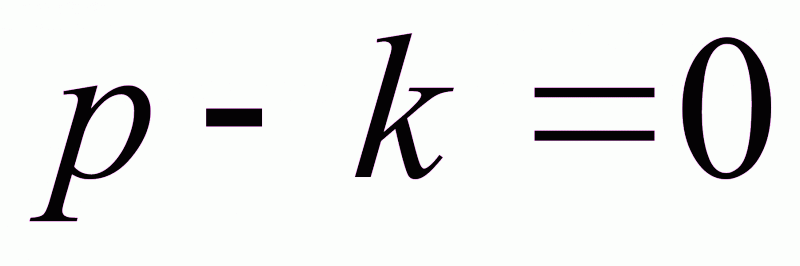
 где
k – устойчивость >0
где
k – устойчивость >0
![]()
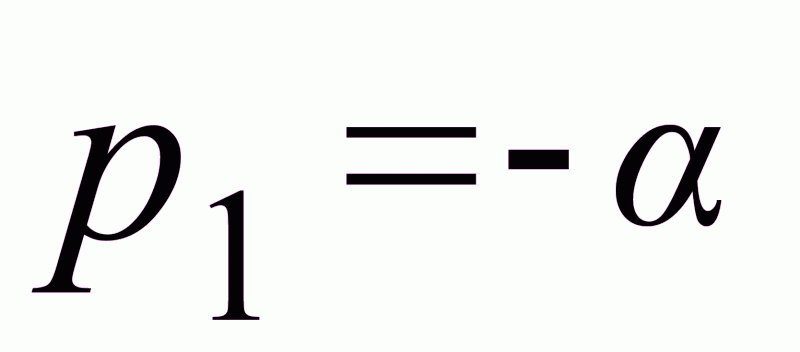
 =1
=1
U=-y
 -
-
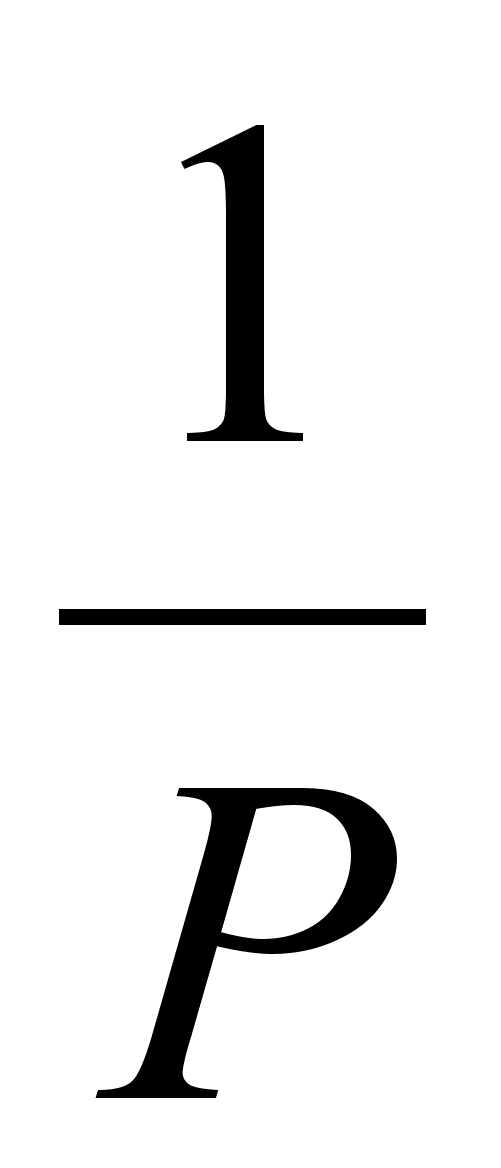
БОГ
G
Рис. 1.13. Функциональная схема градиентной экстремальной системы первого порядка
Этот способ годится только для унимодальных систем, т.е. систем с одним глобальным экстремумом.
1.5.2. Метод тяжёлого шарика
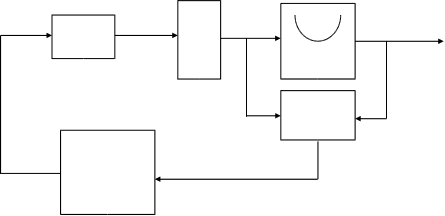
По аналогии с шариком, который скатывается в овраг и проскакивает точки локальных экстремумов, система АУ с колебательными процессами также проскакивает локальные экстремумы. Для обеспечения колебательных процессов в систему первого порядка вводим дополнительную инерционность.
 -
-
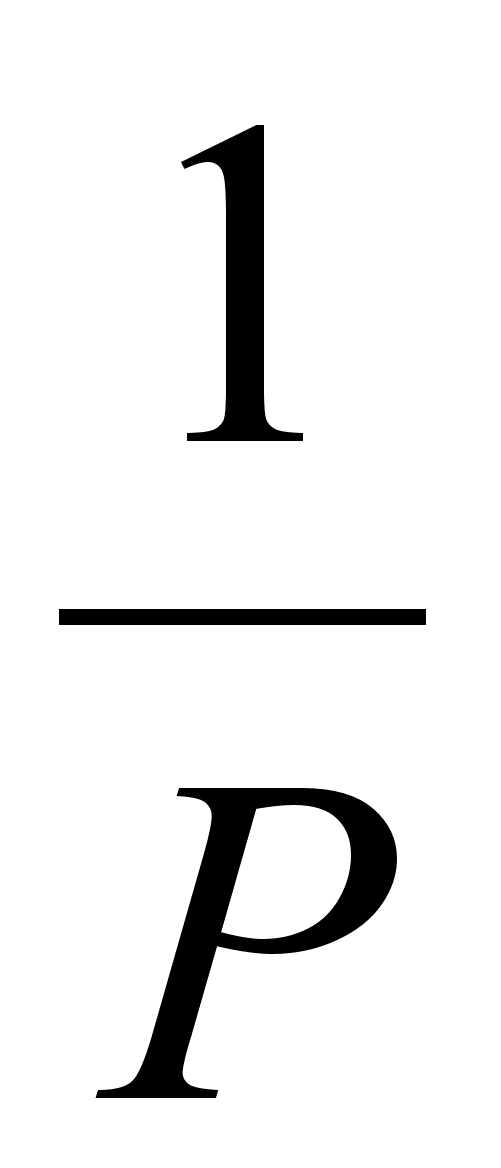
БОГ T-?
 G
G
Рис. 1.14. Иллюстрация метода “тяжёлого” шарика

G =
y; 
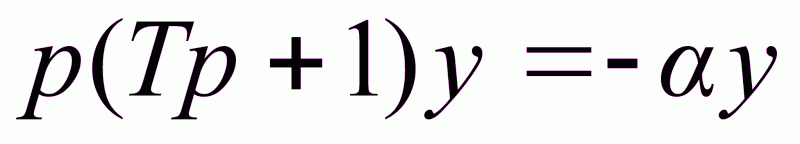 -
уравнение
замкнутой
системы;
-
уравнение
замкнутой
системы;
 - характеристическое
уравнение
системы. (1.26)
- характеристическое
уравнение
системы. (1.26)
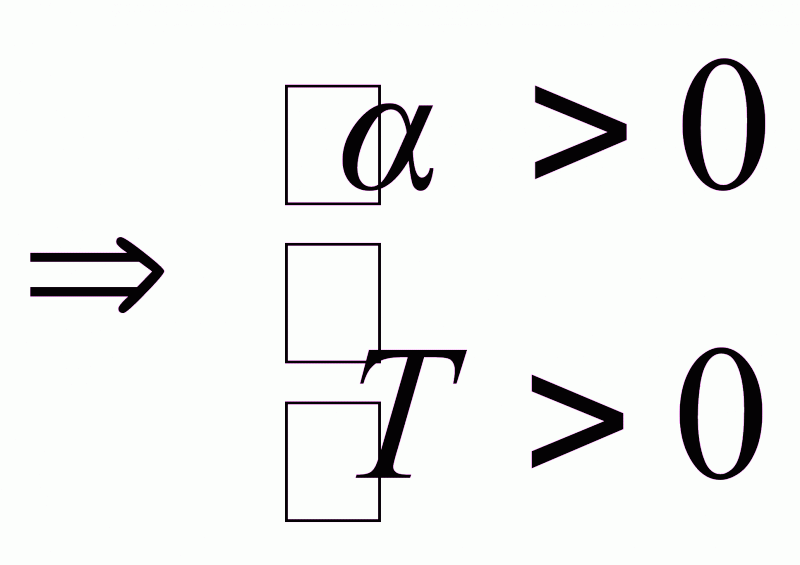


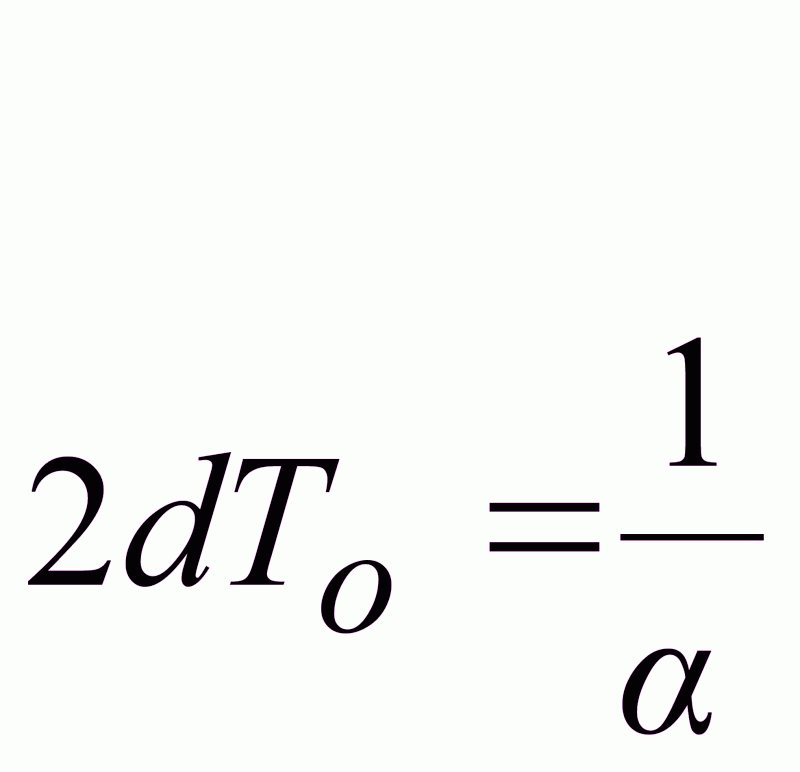 d<1 (1.27)
d<1 (1.27)
Чем меньше d тем длиннее переходный процесс.
Анализируя экстремальную характеристику, задаются необходимые перерегулирование и длительность переходного процесса, откуда задаются:
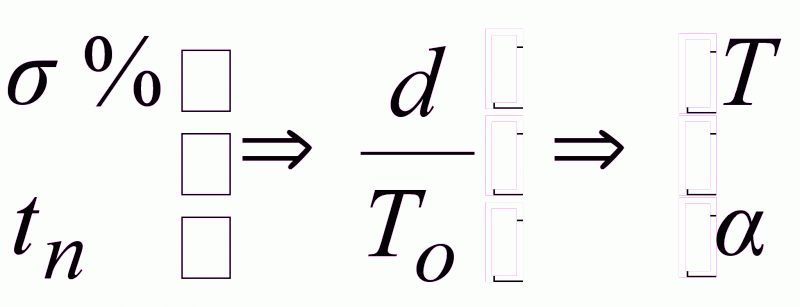
1.5.3. Одноканальные системы общего вида
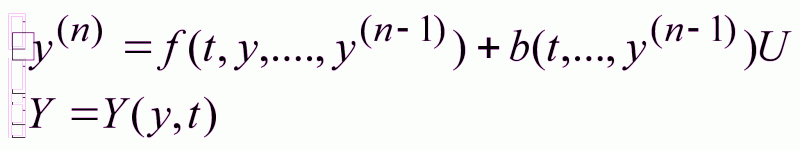 (1.28)
(1.28)
Закон
управления:

Подставив
закон управления
в управление
объекта, получим
уравнение
замкнутой
системы: 
![]()
 (1.29)
(1.29)
В общем случае, для анализа устойчивости замкнутой системы необходимо использовать второй метод Ляпунова, с помощью которого определяется коэффициент усиления регулятора. Т.к. 2й метод Ляпунова даёт лишь достаточное условие устойчивости, то выбранная функция Ляпунова может оказаться неудачной и регулярную процедуру расчёта регулятора здесь предложить нельзя.
1.5.4. Системы со старшей производной в управлении
Общий случай экстремума объектов
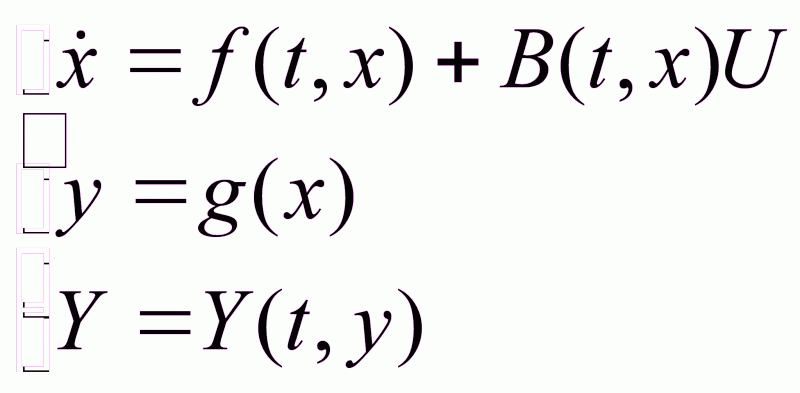
 (1.30)
(1.30)
Функции f, B и g должны удовлетворять условиям существования и единственности решения дифференциального уравнения. Функция g – должна быть многократно дифференцируемой.
С – матрица
производных
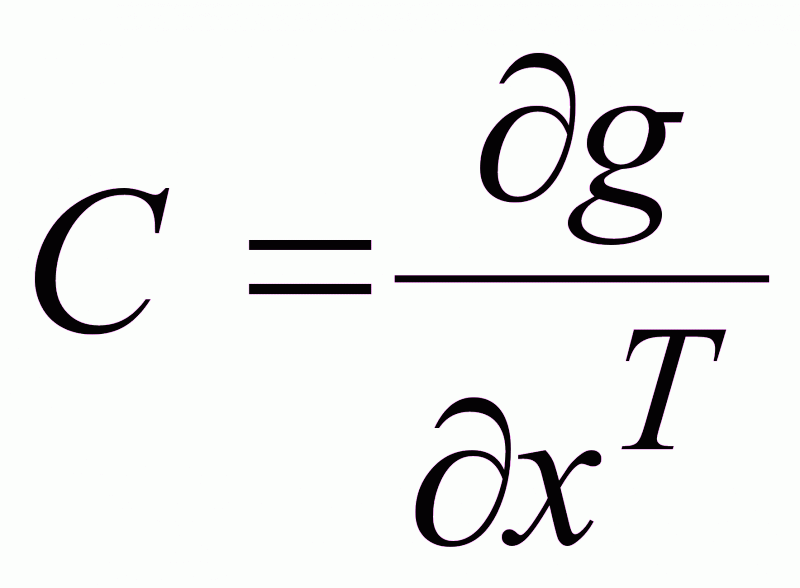 ;
; 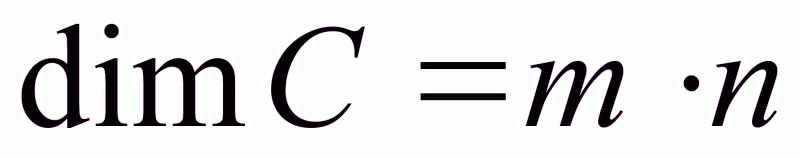
Задача
синтеза разрешима,
если матрица
произведений
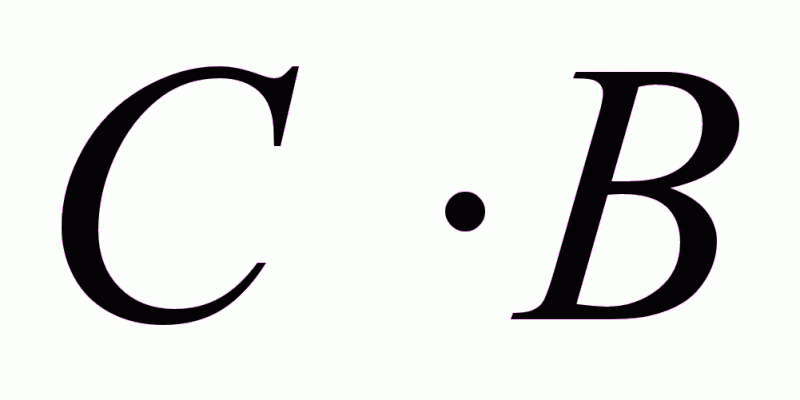 будет не вырожденна,
т.е.
будет не вырожденна,
т.е.
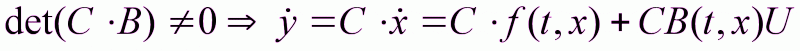 (1.31)
(1.31)
Анализ
условия разрешимости
задачи синтеза
позволяет
определить
производную
выходных переменных,
которая явно
зависит от
управляющего
воздействия.
Если выполняется
условие (1.31), то
такой производной
является первая
производная
 ,
а следовательно
требования
к поведению
замкнутой
системы можно
формировать
в виде дифференциального
уравнения для
y, соответствующего
порядка.
,
а следовательно
требования
к поведению
замкнутой
системы можно
формировать
в виде дифференциального
уравнения для
y, соответствующего
порядка.

![]()


Сформируем
закон управления
замкнутой
системы, для
чего сформируем
закон управления,
подставив в
правую часть
управления
для
 :
:
 -
уравнение
замкнутой
системы относительно
выходной переменной.
-
уравнение
замкнутой
системы относительно
выходной переменной.
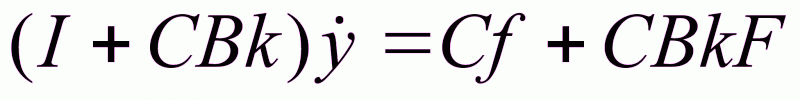
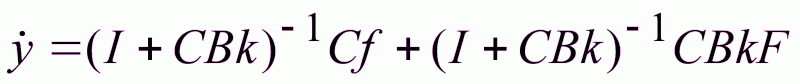 (1.34)
(1.34)
Рассмотрим
ситуацию, когда

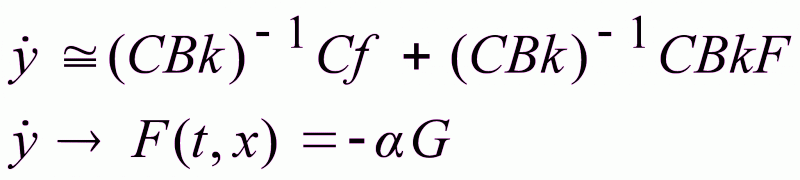
 (1.35)
(1.35)
При соответствующем выборе коэффициента усиления мы получаем желаемое уравнение и автоматический выход на экстремум.
Параметры регулятора выбираются из тех соображений, что и для обычных САУ, т.е.
(СВК)i = (20100), что позволяет обеспечить соответствующую ошибку.
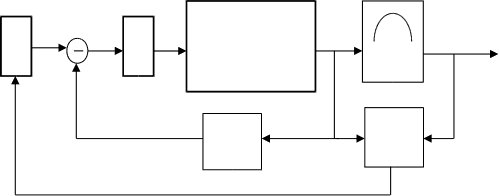
U y Y
F k 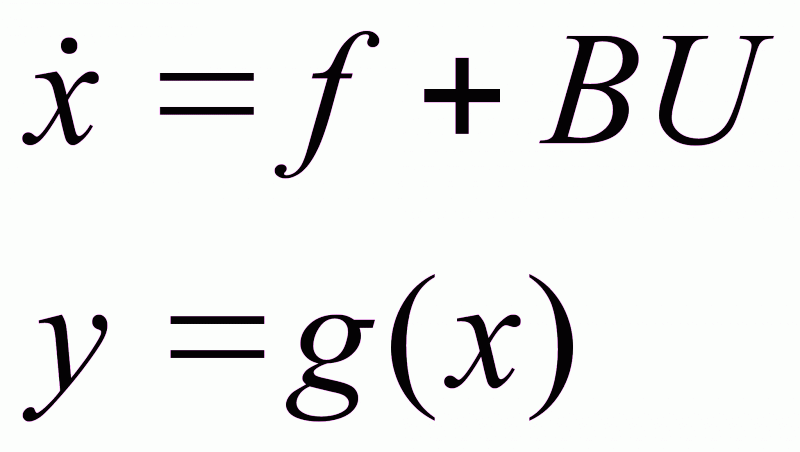
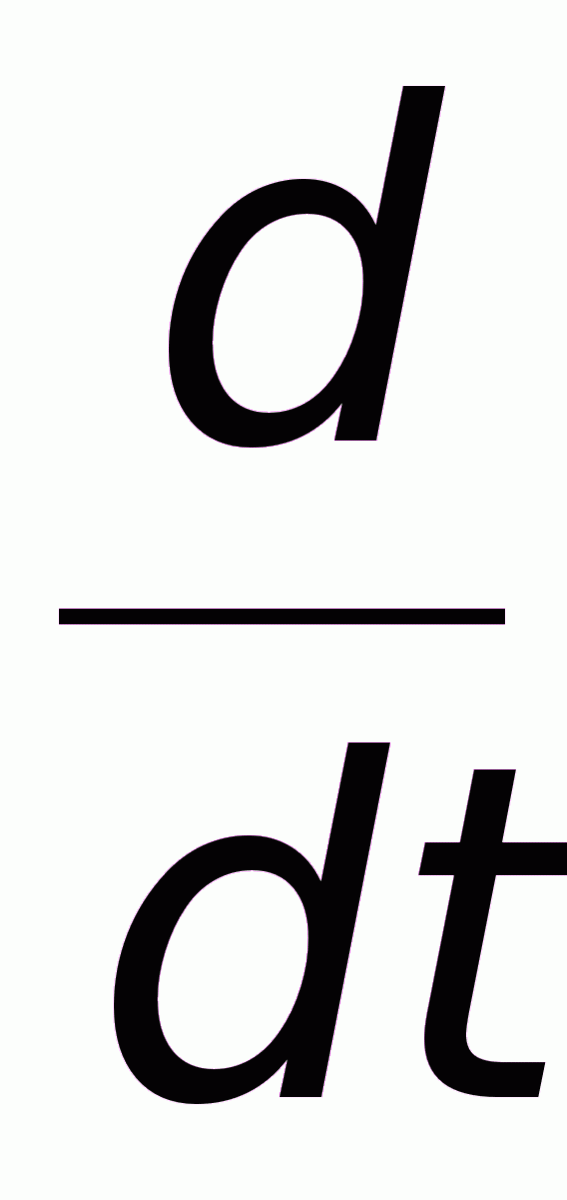 БОГ
БОГ
G
Рис. 1.15. Схема системы со старшей производной в управлении
В системе для оценки полной производной по времени в систему вводят дифференцирующий фильтр, поэтому для оценки градиентов в таких системах удобно использовать фильтр оценки градиента.
Т.к. оба
этих фильтра
имеют малые
постоянные
времени, то в
системе могут
возникать
разнотемповые
процессы, выделить
которые можно
с помощью метода
разделения
движений, причём
медленные
движения будут
описываться
уравнением
(1.34), которое
соответствует
желаемому при
 .
.
Быстрые движения нужно анализировать на устойчивость, причём в зависимости от соотношения постоянной времени ДФ и фильтра оценки частных производных (ФОЧП), можно выделить следующие виды движений:
1) Постоянные времени этих фильтров соизмеримы
Быстрые движения описывают комбинированные процессы в этих двух фильтрах.
2) Постоянные времени различаются на порядок
В системе наблюдаются кроме медленных движений, быстрые и сверх- быстрые движения, соответствующие наименьшей постоянной времени.
На устойчивость необходимо анализировать оба случая.
2. ОПТИМАЛЬНЫЕ СИСТЕМЫ
2.1. Введение
Оптимальные системы – это системы, в которых заданное качество работы достигается за счет максимального использования возможностей объекта, иными словами это системы, в которых объект работает на пределе своих возможностей.
Рассмотрим апериодическое звено первого порядка
K
W (p) = ——― , (2.1)
Tp+1
│u│≤ A, (2.2)
для которого необходимо обеспечить минимальное время перехода у из начального состояния y(0) в конечное yk. Переходная функция такой системы при K=1 выглядит следующим образом
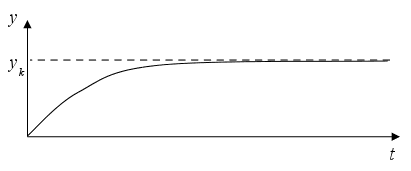
Рис. 2.1. Переходная функция системы при U= const.
Рассмотрим ситуацию, когда на вход объекта подаем максимально возможное управляющее воздействие.
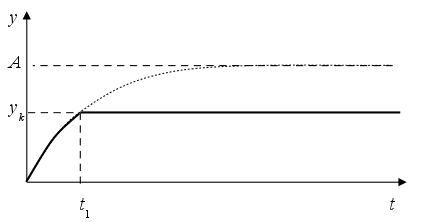
Рис. 2.2. Переходная функция системы при U=A= const.
t1 - минимально возможное время перехода y из нулевого состояния в конечное для данного объекта.
Для получения такого перехода существует два закона управления:
программное управление
![]()
A, t < t1
y = (2.3)
yk, t ≥ t1;
закон управления типа обратной связи
![]()
A, y < yk
y = (2.4)
yk, y ≥ yk;
Второй закон более предпочтителен и позволяет обеспечить управление при помехах.
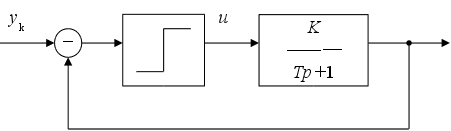
Рис. 2.3. Структурная схема системы с законом управления типа обратной связи.
2.2. Постановка задачи синтеза оптимальных систем.
2.2.1. Математическая модель объекта.
Объект описан переменными состояния
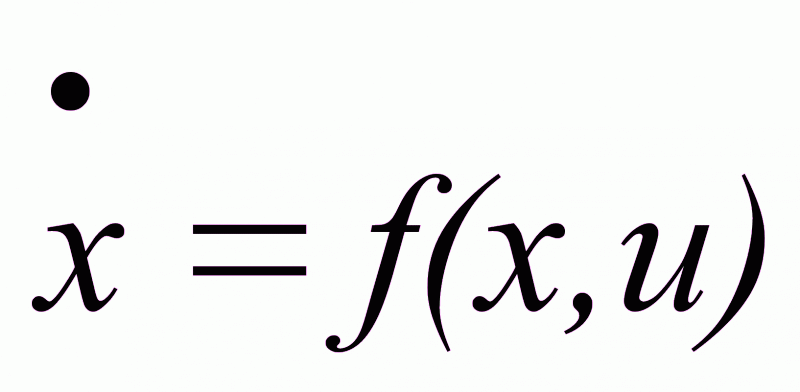 xRn
, uRm,
m ≤ n,
(2.5)
xRn
, uRm,
m ≤ n,
(2.5)
где функция f(x,u) непрерывна, дифференцируема по всем аргументам и удовлетворяет условию существования и единственности решения дифференциального уравнения. Эта функция является нелинейной, но стационарной.
В качестве частных случаев объект может иметь вид нелинейной системы с аддитивным управлением
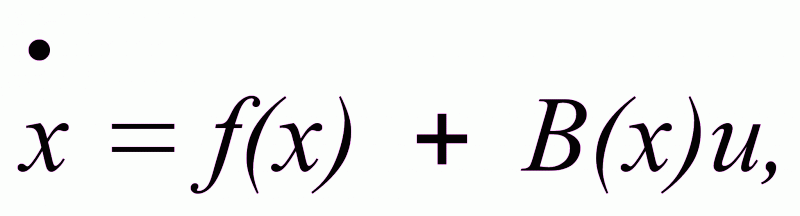 (2.6)
(2.6)
либо линейной системой
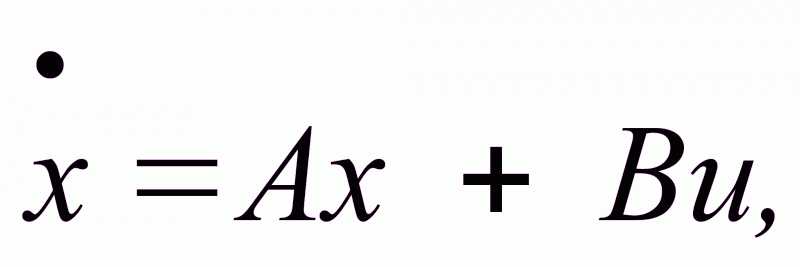 (2.7)
(2.7)
Объект должен быть представлен в одной из трех форм, представленных выше.
2.2.2. Множество начальных и конечных состояний.
Задача оптимального перехода из начального состояния в конечное представляет собой краевую задачу, где начальные и конечные точки могут быть заданы одним из четырех способов, представленных на рис. 2.4.

Рис.2.4. Фазовые портреты перехода системы из начального состояния в конечное для различных задач:
а) задача с фиксированными концами,
б) задача с фиксированным первым концом (фиксированная начальная точка и множество конечных значений),
в) задача с фиксированным правым концом,
г) задача с подвижными концами.
Для объекта множество начальных состояний может в общем случае совпадать с о всем множеством состояний либо с рабочей областью, а множество конечных состояний является подпространством множества состояний или рабочей области.
Пример 2.1.
В любую ли точку пространства состояний можно перевести объект, описываемый системой уравнений ?
- x10 – x20 + 2u = 0;
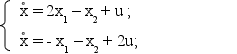
Запишем уравнения статики для данного объекта
2x10 – x20 + u = 0;
Подставив во второе уравнение значение U из первого уравнения u = x20 – 2x10, получим
-5x10 + x20 = 0;
Получили множество конечных состояний, описываемое уравнением
x20 = 5x10;
Таким образом, множество конечных состояний, задаваемое для объекта (системы), должно быть реализуемым.
2.2.3. Ограничения на состояния и управление

Рис. 2.5. Общий вид рабочей области пространства состояний.
Выделяется рабочая область пространства состояний, которая оговаривается. Как правило, эта область описывается ее границами с помощью модульных соглашений.

Рис.2.6. Вид рабочей области пространства состояний,
заданной модульными соглашениями.
Также задается U – область допустимых значений управляющего воздействия. На практике область U задается также с помощью модульных соотношений.
![]() Ui
≤
Ūi,
Ui
≤
Ūi,
Задача синтеза оптимального регулятора решается при условии ограничений на управление и ограниченном ресурсе.
2.2.4. Критерий оптимальности.
На этом этапе оговариваются требования, предъявляемые к качеству работы замкнутой системы. Требования задаются в обобщенном виде, а именно в виде интегрального функционала, который носит название критерия оптимальности.
Общий вид критерия оптимальности:
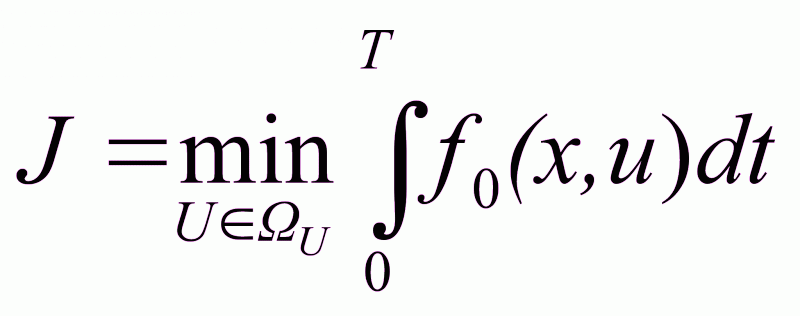 , (2.8)
, (2.8)
Частные виды критерия оптимальности:
1) критерий оптимальности, обеспечивающий минимум времени переходного процесса (решается задача оптимального быстродействия)
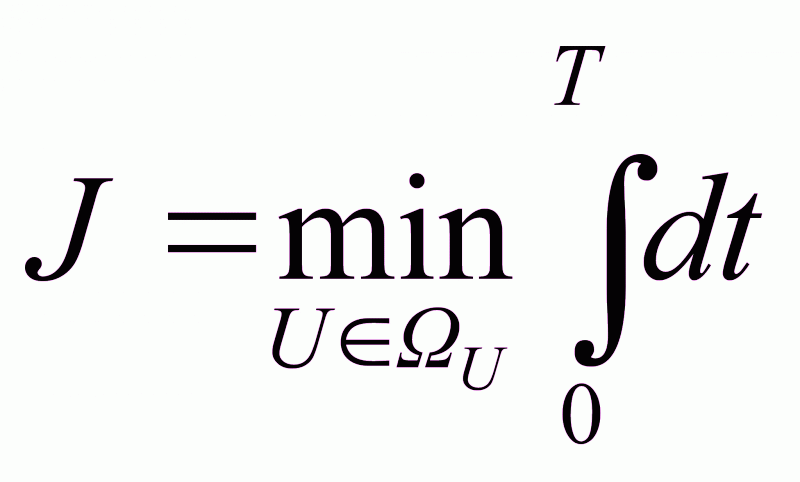 ; (2.9)
; (2.9)
2) критерий оптимальности, обеспечивающий минимум затрат энергии:
по одной из компонент
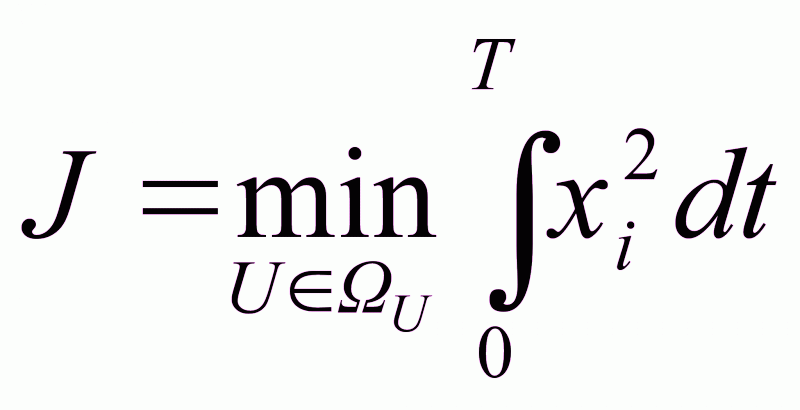 ; (2.10)
; (2.10)
по всем переменным состояниям
 ; (2.11)
; (2.11)
по одному управляющему воздействию
 ; (2.12)
; (2.12)
по всем управляющим воздействиям
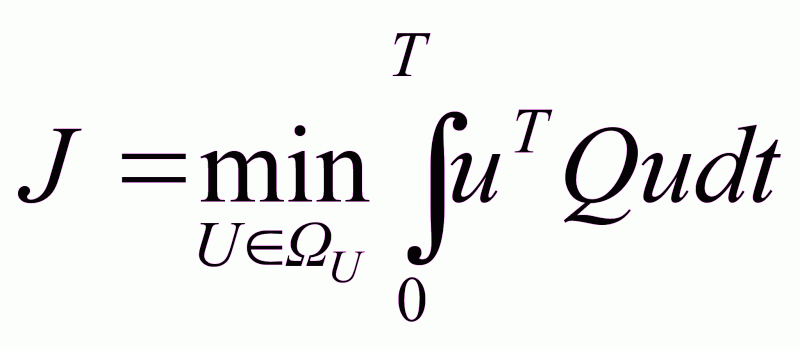 ; (2.13)
; (2.13)
по всем компонентам (в самом общем случае)
 .
(2.14)
.
(2.14)
2.2.5. Форма результата
Необходимо оговорить в каком виде будем искать управляющее воздействие.
Возможны два варианта оптимального управления U0:
u0 = u0(t) – используется при отсутствии возмущения,
u0 = u0(x) – оптимальное управление в виде обратной связи (замкнутое управление).
Формулировка задачи синтеза оптимальной системы в общем виде:
Для объекта, описанного переменными состояниями с заданными ограничениями и множеством начальных и конечных состояний, необходимо найти управляющее воздействие, обеспечивающее качество процессов в замкнутой системе, соответствующее критерию оптимальности.
2.3. Метод динамического программирования
2.3.1. Принцип оптимальности
Исходные данные:
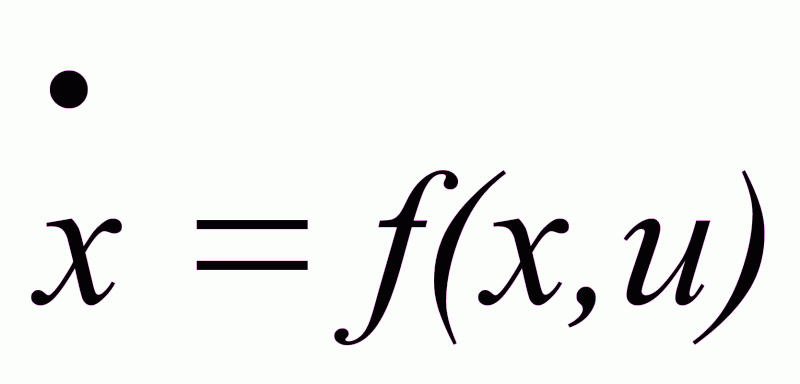 ,
xRn
, uRm,
m ≤ n,
,
xRn
, uRm,
m ≤ n,
ui ≤ Ūi, x(0), x(T) ,
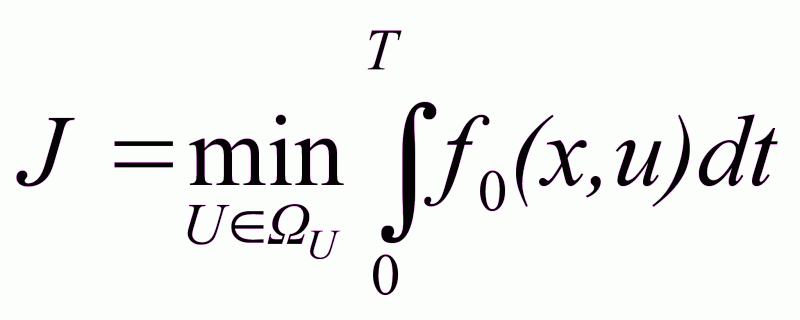

Необходимо найти u0
Рис. 2.7. Фазовый портрет перехода системы из начальной точки в конечную
в пространстве состояний
Траектория перехода из начальной точки в конечную будет оптимальной и единственной.
Формулировка принципа:
Конечный участок оптимальной траектории есть также оптимальная траектория.
Если бы переход из промежуточной точки в конечную не осуществлялся бы по оптимальной траектории, то для него можно было бы найти свою оптимальную траекторию. Но в этом случае переход из начальной точки в конечную проходил бы по другой траектории, которая должна была бы быть оптимальной, а это невозможно, так как оптимальная траектория единственная.
2.3.2. Основное уравнение Беллмана.
Рассмотрим объект управления произвольного вида
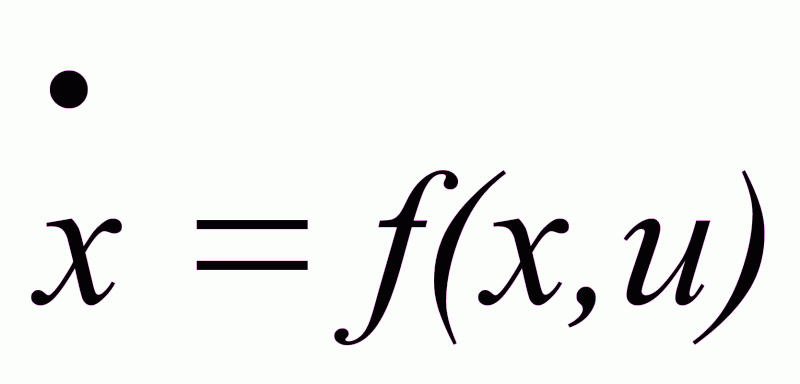 ,
xRn
, uRm,
m ≤ n,
,
xRn
, uRm,
m ≤ n,
Необходимо обеспечить переход из начальной точки в конечную с критерием оптимальности
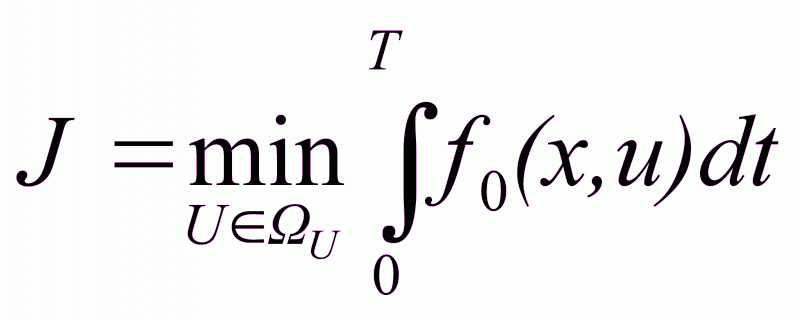 . (2.16)
. (2.16)
Рассмотрим переход в пространстве состояний
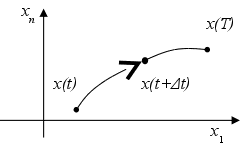
Рис. 2.8. Фазовый портрет перехода системы из начальной точки в конечную
x(t) – текущая (начальная) точка, x(t+Δt) – промежуточная точка.
В ыберем
промежуточную
точку и рассмотрим
поэтапный
переход
ыберем
промежуточную
точку и рассмотрим
поэтапный
переход
(2.17)
Преобразуем выражение
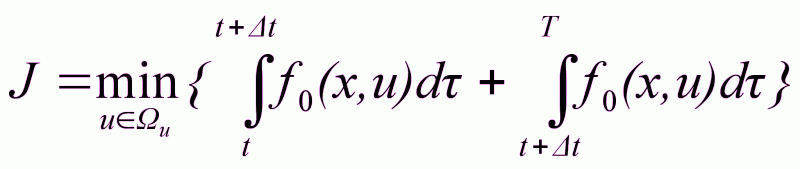 (2.18)
(2.18)
Заменим второй интеграл на V(x(t+Δt))
 (2.19)
(2.19)
При малом значении Δt βведем допущения:
1)
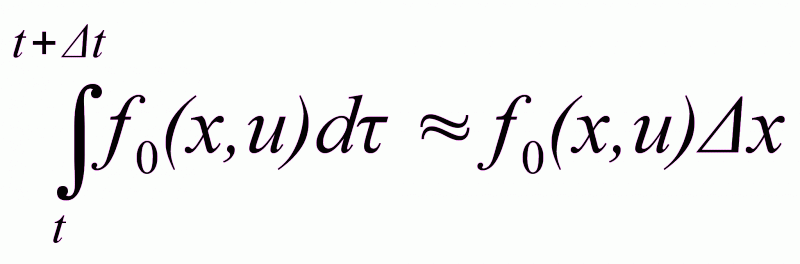 (2.20)
(2.20)
2) Разложим вспомогательную функцию
 ,
(2.21)
,
(2.21)
 (2.22)
(2.22)
Выполняя дальнейшие преобразования, получим
 ,
(2.23)
,
(2.23)
где min V(x(t)) и есть критерий оптимальности J
В результате получили
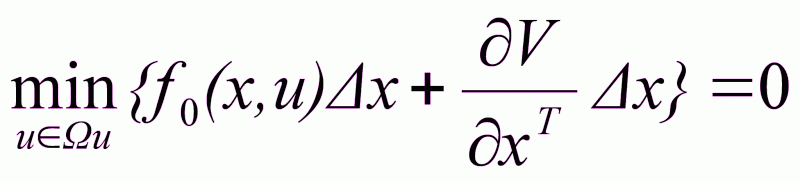 .
(2.24)
.
(2.24)
Разделим обе части выражения на Δt и устраним Δt к нулю.
 ,
(2.25)
,
(2.25)
где
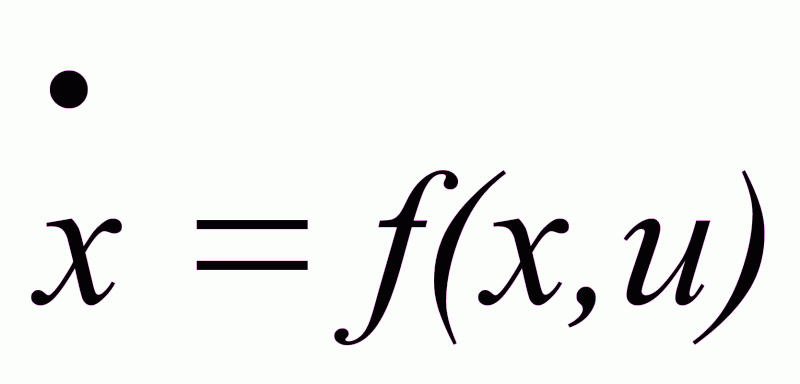
Получим основное уравнение Беллмана
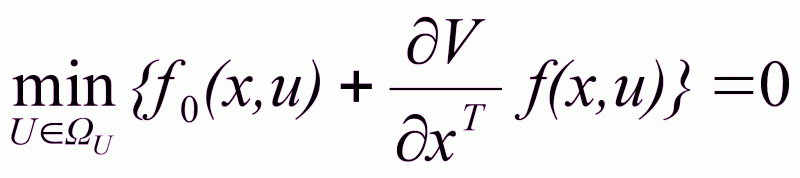 (2.26)
(2.26)
2.2.3. Расчетные соотношения метода динамического программирования
Основное уравнение Белмана содержит (m+1) - неизвестных величин, т.к. U0Rm , VR1
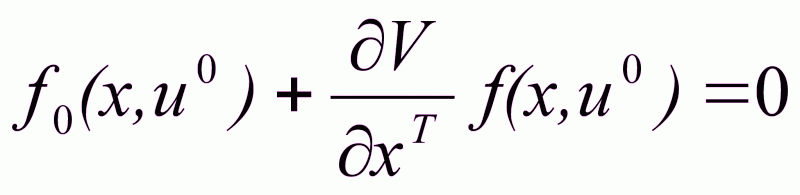
![]() (2.27)
(2.27)

Продифференцировав m раз, получим систему из (m+1) уравнений.
Для ограниченного круга объектов решение полученной системы уравнений дает точное оптимальное управление. Такая задача носит название задачи АКОР (аналитического конструирования оптимальных регуляторов).
Объекты, для которых рассматривается задача АКОР, должны удовлетворять следующим требованиям:
1)
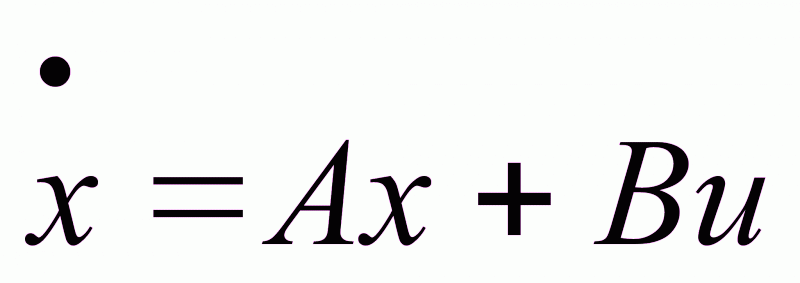
T ,
Критерий оптимальности должен быть квадратичным
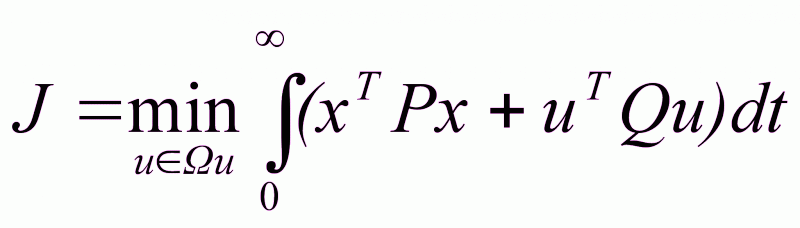 .
.
Пример 2.2
Для объекта, описываемого уравнением
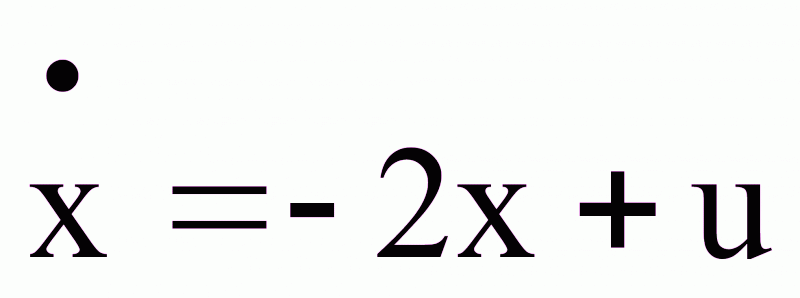 ,
,
необходимо обеспечить переход из x(0) в x(T) по критерию оптимальности
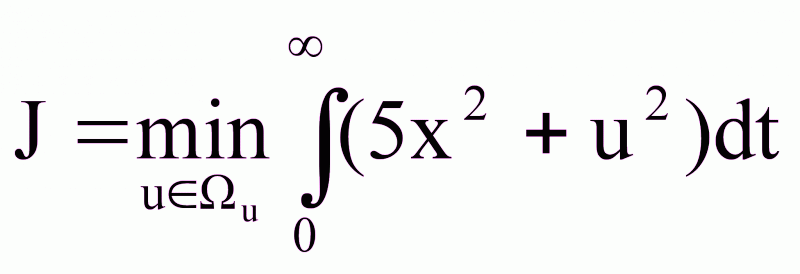 ,
,
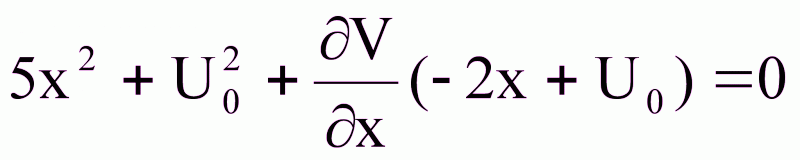
![]()
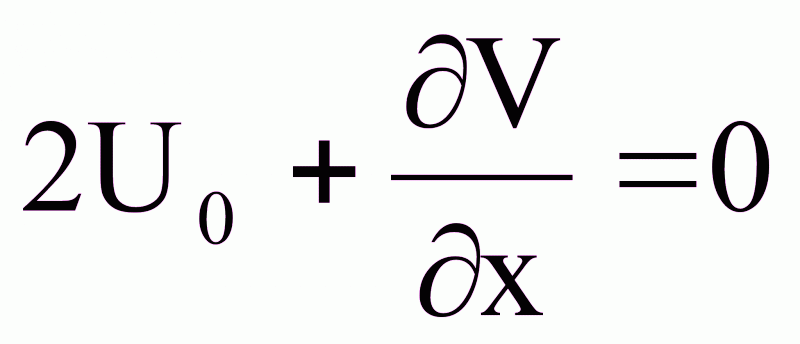
U1= 5x,
U2= -6x
Проанализировав объект на устойчивость, получим U0 = U2 = -6x.
2.4. Принцип максимума Понтрягина
 (2.28)
(2.28)
или
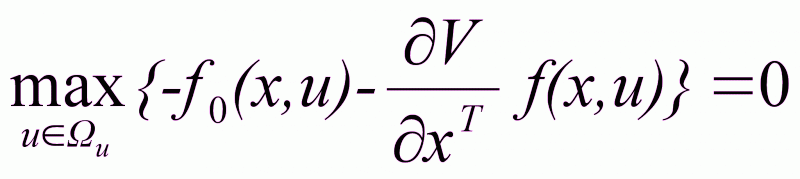 (2.29)
(2.29)
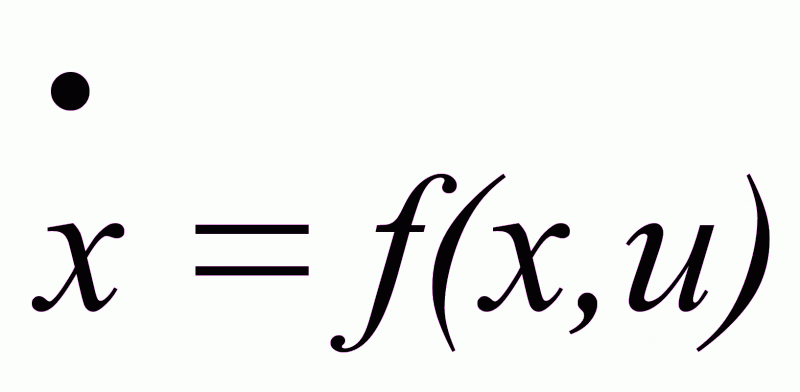
![]()
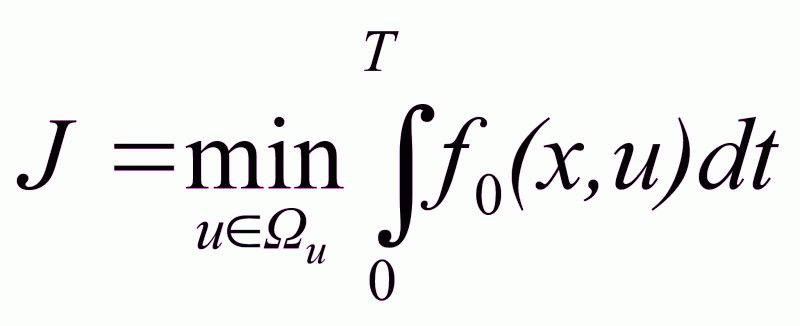
Введем расширенный вектор состояний, который расширяем за счет нулевой компоненты, в качестве которой выбираем критерий оптимальности. zRn+1
 .
(2.30)
.
(2.30)
Также введем расширенный вектор правых частей, который расширяем за счет функции, стоящей под интегралом в критерии оптимальности.

 (2.31)
(2.31)
Введем Ψ – вектор сопряженных координат
 (2.32)
(2.32)
Сформируем Гамильтониан, представляющий собой скалярное произведение Ψ и φ(z,u)
H(Ψ,z,u) = Ψ•φ(z,u), (2.33)
 (2.34)
(2.34)
Уравнение (2.34) называется основным уравнением принципа максимума Понтрягина, основанное на уравнении динамического программирования
Оптимальным является управление, которое на заданном интервале времени доставляет максимум Гамильтониана. Если бы ресурс управления не был бы ограничен, то для определения оптимального управления можно было бы воспользоваться необходимыми и достаточными условиями экстремума. В реальной ситуации для отыскания оптимального управления необходимо анализировать величину Гамильтониана при предельном значении уровня. В этом случае U0 будет функцией расширенного вектора состояний и вектора сопряженных координат
u0 = u0(z, Ψ)
Для отыскания сопряженных координат необходимо решить систему уравнений
 .
.
2.4.1. Процедура расчета системы по принципу максимума Понтрягина.
Уравнения объекта должны быть приведены к виду, стандартному для синтеза оптимальных систем.
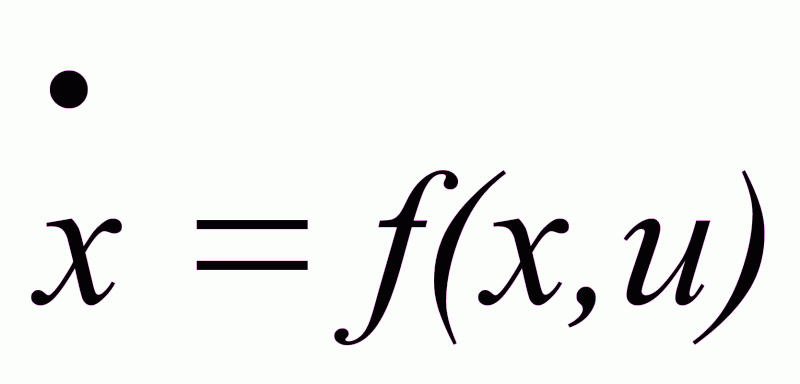 , xRn,
uRm,
m≤n
, xRn,
uRm,
m≤n
Необходимо оговорить также начальные и конечные состояния и записать критерий оптимальности
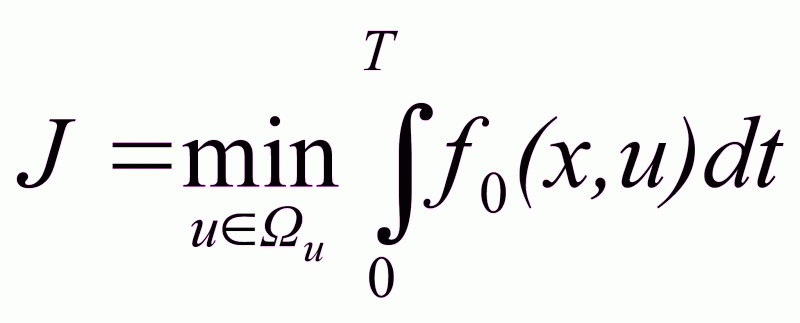 . (2.35)
. (2.35)
Вводятся расширенный вектор состояний
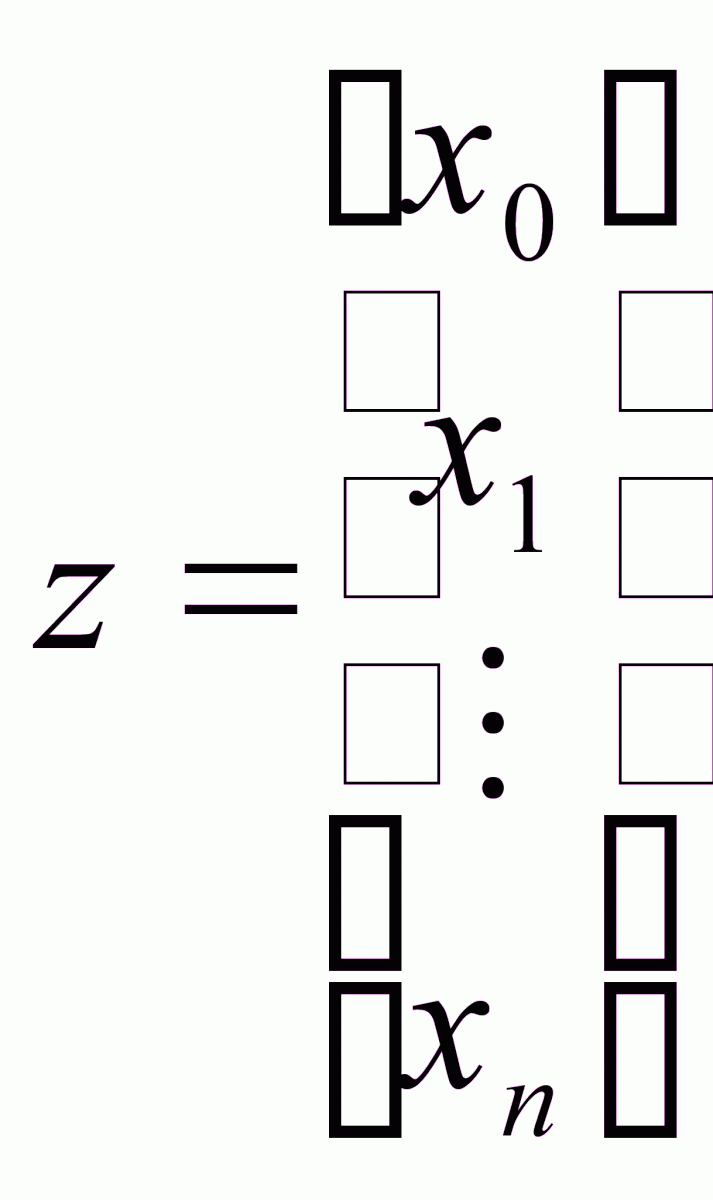 , (2.36)
, (2.36)
расширенный вектор правых частей
 (2.37)
(2.37)
и вектор сопряженных координат
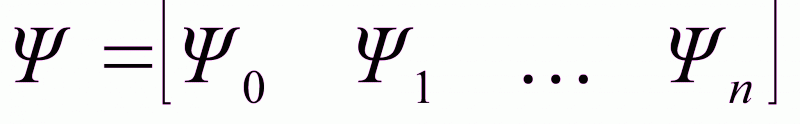 .
(2.38)
.
(2.38)
Записываем Гамильтониан как скалярное произведение
H(Ψ,z,u) = Ψ•φ(z,u), (2.39)
Находим максимум Гамильтониана по u
 ,
(2.40)
,
(2.40)
по которому определяем оптимальное управление u0(Ψ,z).
Записываем дифференциальные уравнения для вектора сопряженных координат
 .
(2.41)
.
(2.41)
Находим сопряженные координаты как функцию времени
Ψ= Ψ(t). (2.42)
6. Определяем окончательный оптимальный закон управления
u0= u0(t) . (2.43)
Как правило, этот способ позволяет получить программный закон управления.
Пример 2.3.
Для объекта, представленного на рис. 2. 9. необходимо обеспечить переход из начальной точки y(t) в конечную y(t) за T= 1c с качеством процесса
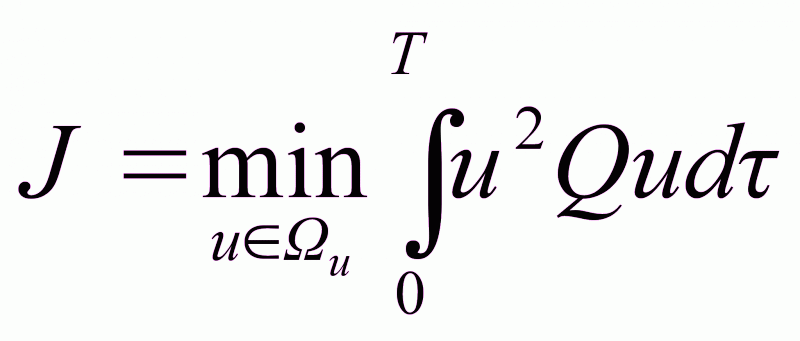
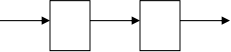 U y
U y
Рис. 2.9. Модель объекта
W
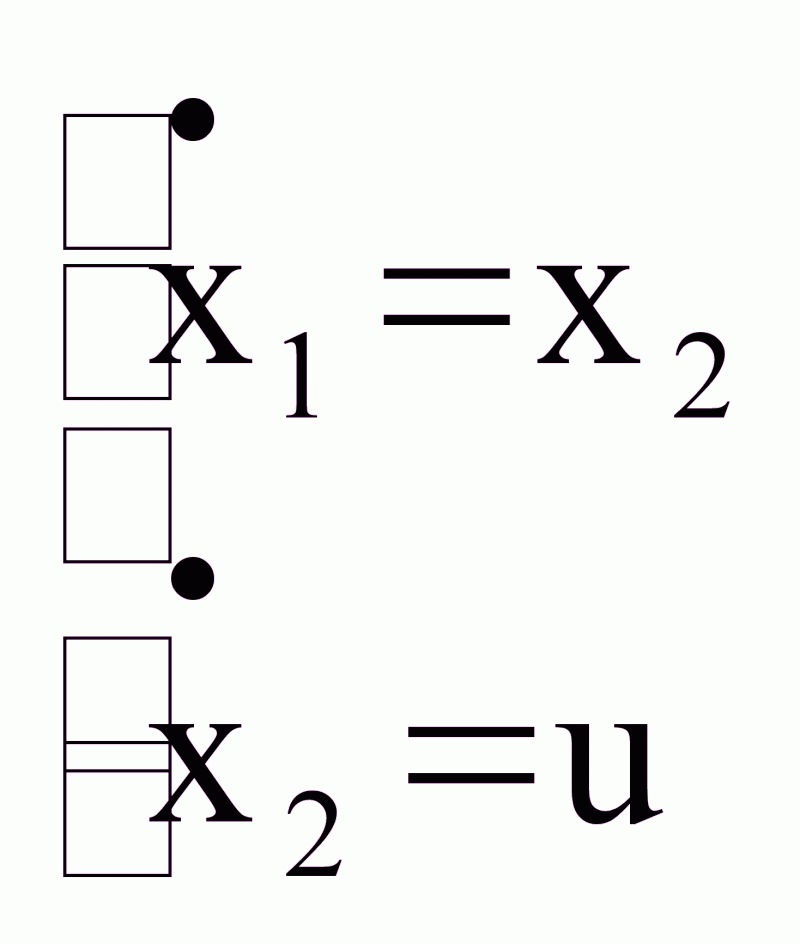
(p)=y/U = 1/p2
![]()
![]() x1(0)=0 x1(T)=1
x1(0)=0 x1(T)=1
x2(0)=0 x2(T)=0
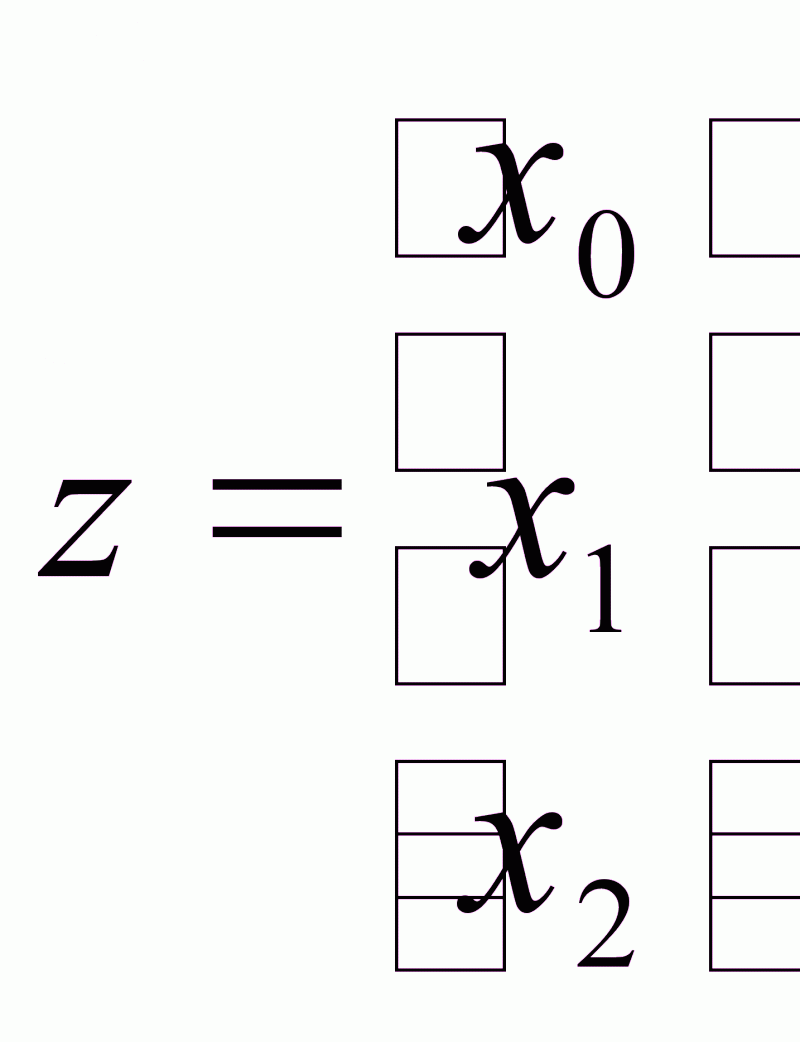 ,
,  ,
,  .
.
3.
H(Ψ,Z,U) = Ψ0u2 + Ψ1x2 + Ψ3u.
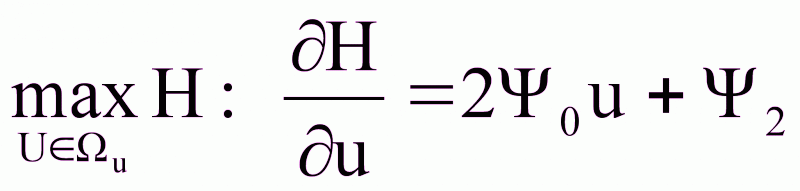 ,
,
u0= - Ψ2/2 Ψ0.
5.

6.
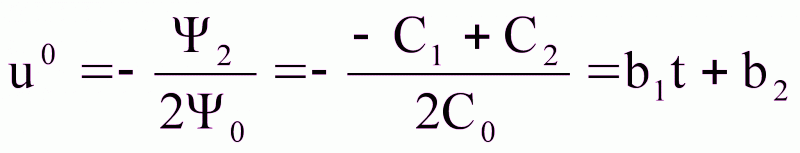
Для определения констант b1 и b2 нужно решить краевую задачу.
З
апишем
уравнение
замкнутой
системы
П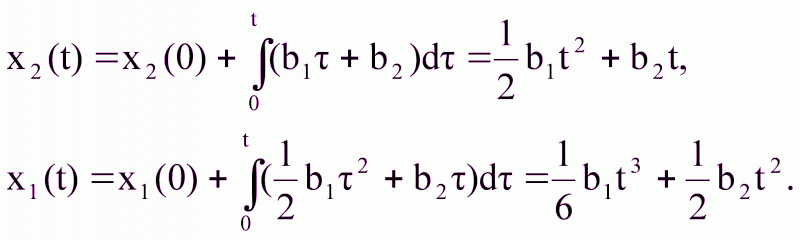
роинтегрируем
Рассмотрим конечную точку t=T=1с.
![]() x1(T)=1
x1(T)=1
x2(T)=0
![]() 1= 1/6 b1
+ 1/2 b2
1= 1/6 b1
+ 1/2 b2
0= 1/2b1 + b2
Получили систему уравнений, из которой находим b2 = 6, b1 = -12.
Запишем закон управления u0= -12t + 6.
2.4.2. Задача оптимального управления
 , xRn,
uRm,
m≤n
, xRn,
uRm,
m≤n
Для объекта общего вида необходимо обеспечить переход из начальной точки в конечную за минимальное время при ограниченном законе управления.
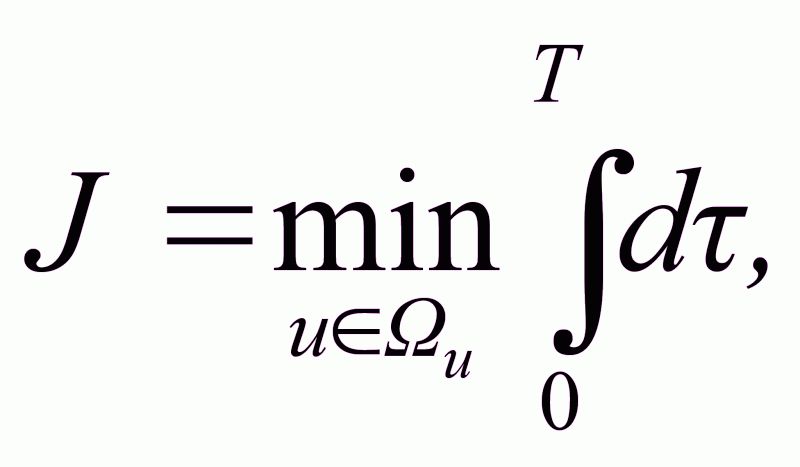
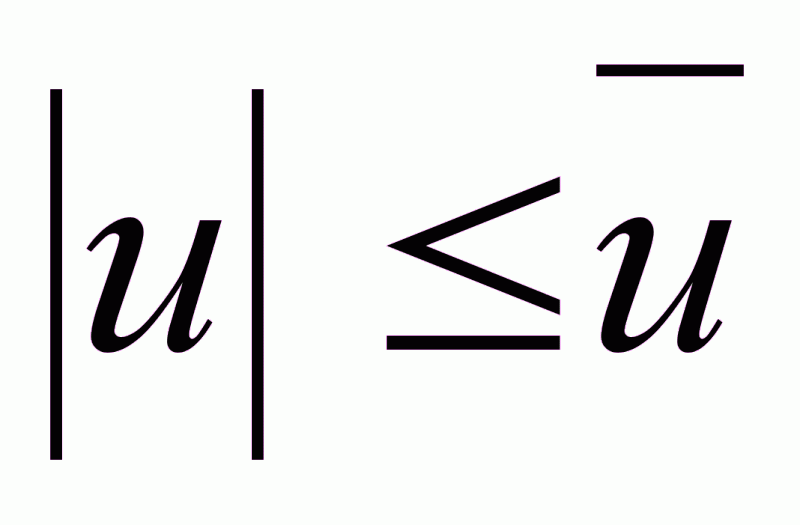 .
(2.44)
.
(2.44)
Особенности задачи оптимального быстродействия
Гамильтониан быстродействия.
H = Ψ▪φ = Ψ0▪1 + Ψ1▪f1(x,u) +…+ Ψn▪fn(x,u), (2.45)
Ψ0=-1. (2.46)
H = -1 + Ψ1▪f1(x,u) +…+ Ψn▪fn(x,u), (2.47)
Hб
= Ψ1▪f1(x,u)
+…+ Ψn▪fn(x,u)
= ▪f(x,u)
(2.48)
▪f(x,u)
(2.48)
 =[Ψ1,…,
Ψn]
(2.49)
=[Ψ1,…,
Ψn]
(2.49)
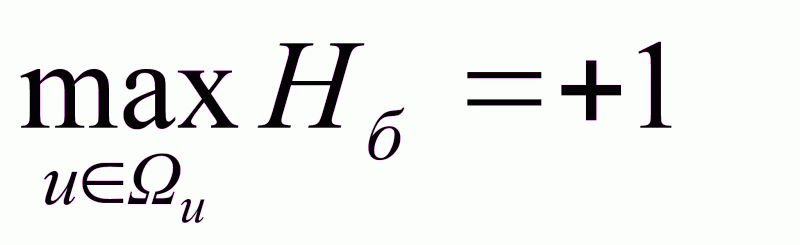 .
(2.50)
.
(2.50)
Релейность управления.
Эта особенность имеет место для релейных объектов.
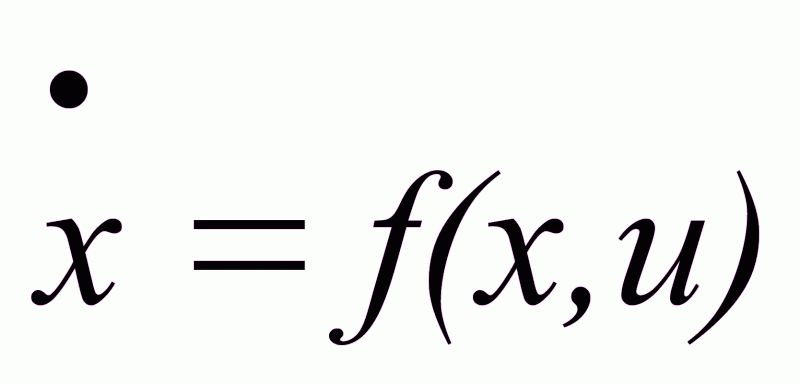 , xRn,
uRm,
m≤n,
, xRn,
uRm,
m≤n,
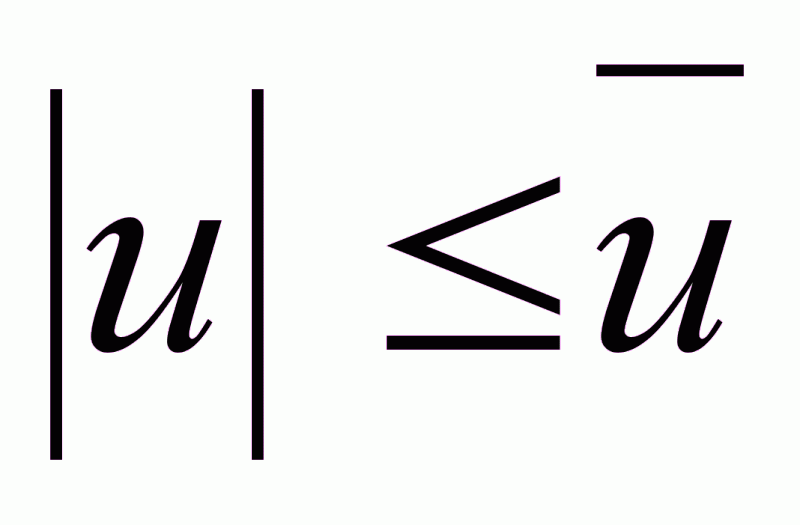
Hб
=
 ▪(Ax+Bu);
▪(Ax+Bu);
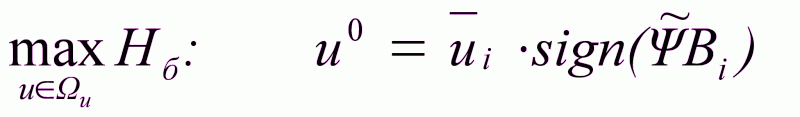
Теорема о числе переключений управляющего воздействия.
Эта теорема справедлива для линейных моделей с вещественными корнями характеристического уравнения.
det(pI-A)=0 (2.51)
Λ(A) – вектор вещественных собственных чисел.
Формулировка теоремы:
В задаче оптимального быстродействия с вещественными корнями характеристического уравнения число переключений не может быть больше, чем (n-1), где n – порядок объекта, следовательно, число интервалов постоянства управления не будет больше, чем (n-1).

Рис. 2.10. Вид управляющего воздействия при n=3.
Пример2.4
.
Рассмотрим пример решения задачи оптимального быстродействия:
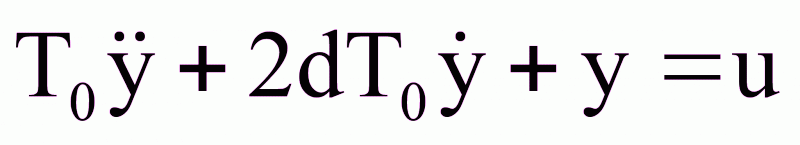 ,
,  ,
T0=1
,
T0=1
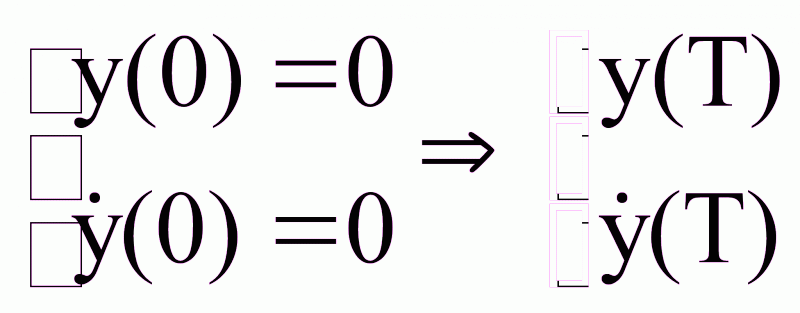 ,
, 
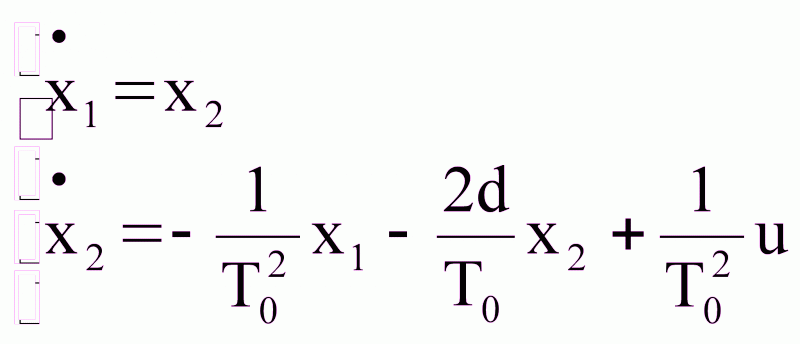 .
.
Ψ=[Ψ1, Ψ2].
Hб= Ψ1x2+ Ψ2( -2dx2 –x1+u).
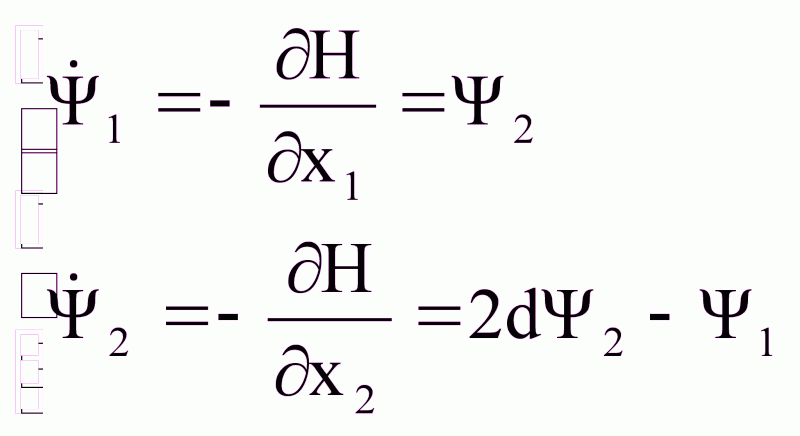 ,
,
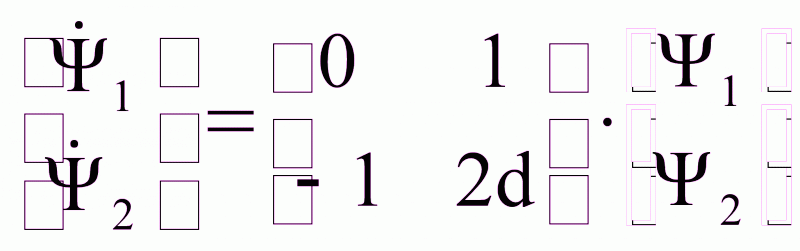 ,
,
 .
.
29-04-2015, 04:06