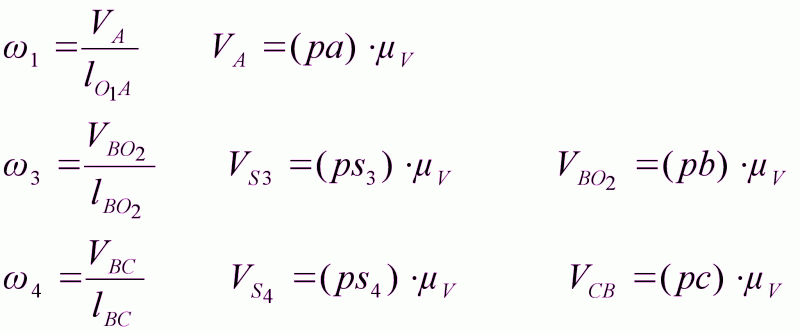
С учетом этого формула принимает вид
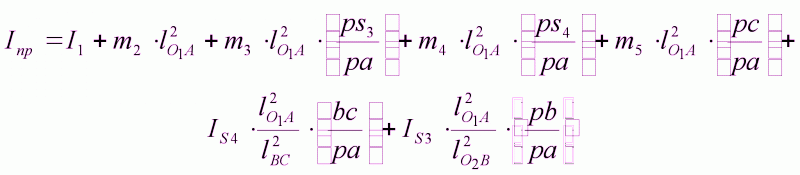
Полученные значения сводим в таблицу:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7 | 8 | 9 | 10 | 11 | |
|
pc3 |
0 | 16 | 22 | 24 | 25 | 22 | 15 | 7 | 0 | 6 | 21 | 29 | 10 |
| pb | 0 | 52 | 59 | 61 | 61 | 57 | 44 | 21 | 0 | 27 | 111 | 140 | 50 |
| bc | 0 | 15 | 9 | 6 | 2 | 10 | 13 | 10 | 0 | 12 | 29 | 10 | 17 |
|
ps4 |
0 | 55 | 59 | 62 | 63 | 56 | 41 | 18 | 0 | 23 | 106 | 141 | 49 |
| pc | 0 | 54 | 62 | 63 | 63 | 54 | 59 | 16 | 0 | 21 | 102 | 142 | 53 |
|
Iпр |
0 | 1,91 | 3,23 | 3,73 | 3,98 | 3,05 | 1,81 | 0,3 | 0 | 0,28 | 4,49 | 8,54 | 1,09 |
По результатам
строим график
Iпр=
Iпр( )
)
3). Построение диаграммы энергомасс.
Построение
этой диаграммы
выполняют путем
исключения
параметра
 из диаграмм
из диаграмм
 Т(
Т( )
и Iпр(
)
и Iпр( ).
В результате
получают диаграмму
энергомасс
).
В результате
получают диаграмму
энергомасс
 Т(
Т( )
=
)
= Т(Iпр).
График Iпр(
Т(Iпр).
График Iпр( )
целесообразно
расположить
так чтобы ось
Iпр была
горизонтальной,
а
)
целесообразно
расположить
так чтобы ось
Iпр была
горизонтальной,
а
 –вертикальной.
Положение осей
диаграммы
энергомасс
увязывают с
диаграммами
–вертикальной.
Положение осей
диаграммы
энергомасс
увязывают с
диаграммами
 Т(
Т( )
и Iпр(
)
и Iпр( ).
После нахождения
всех точек
диаграммы
энергомасс
их соединяют
сплавной линией,
в результате
чего получается
кривая Виттенбауэра.
).
После нахождения
всех точек
диаграммы
энергомасс
их соединяют
сплавной линией,
в результате
чего получается
кривая Виттенбауэра.
5.3. Определение размеров маховика.
Углы наклона касательных к кривой Виттенбауэра определим по формулам:
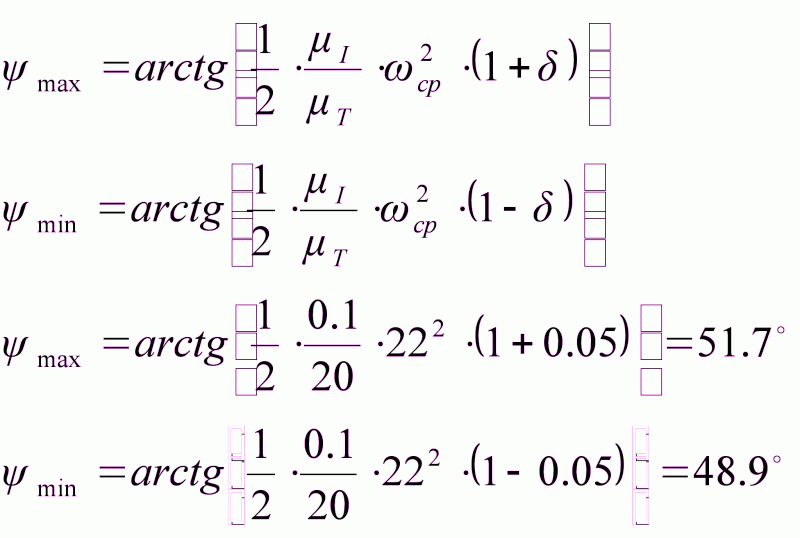
После нахождения
углов проводят
две касательные
к кривой Виттенбауэра,
при этом они
ни в одной точке
не должны пересекать
кривую Виттеннбауэра.
Касательные
на оси
 Т
отсекают отрезок
ab , с помощью
которого находится
постоянная
составляющая
приведенного
момента инерции
рычажного
механизма,
обеспечивающая
движение звена
приведения
с заданным
коэффициентом
неравномерности
движения:
Т
отсекают отрезок
ab , с помощью
которого находится
постоянная
составляющая
приведенного
момента инерции
рычажного
механизма,
обеспечивающая
движение звена
приведения
с заданным
коэффициентом
неравномерности
движения:
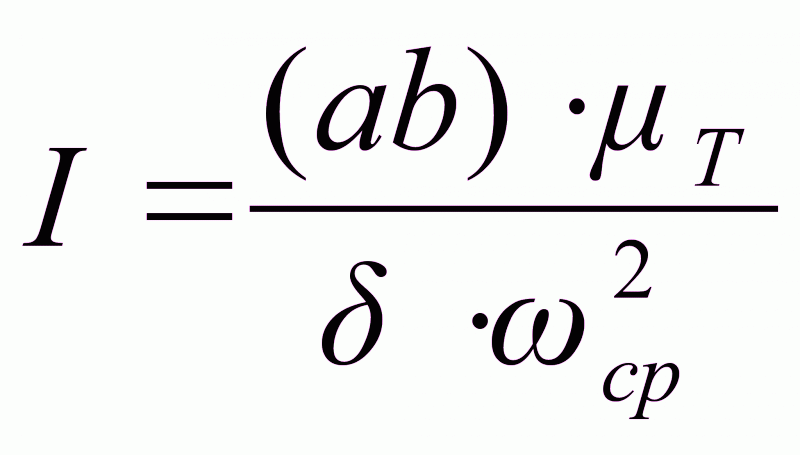 ;
;
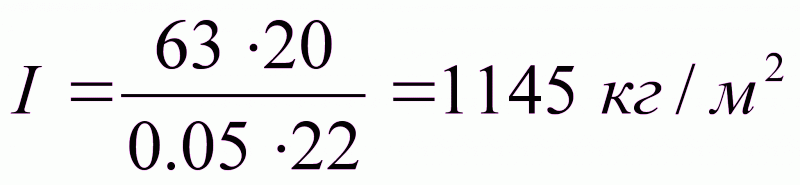
Определение частоты вращения маховика:
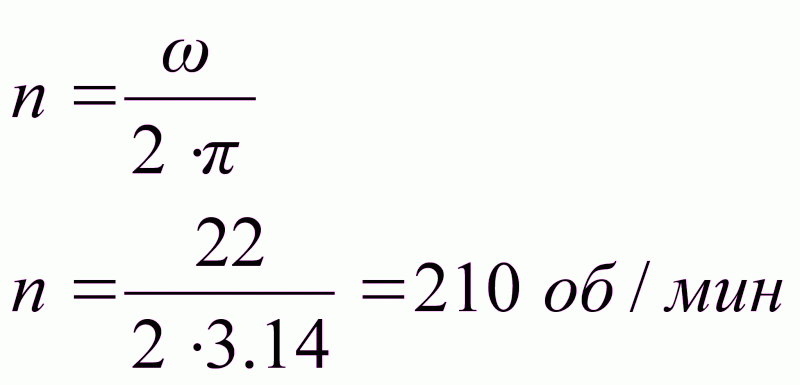
Принимаем материал маховика–чугун.
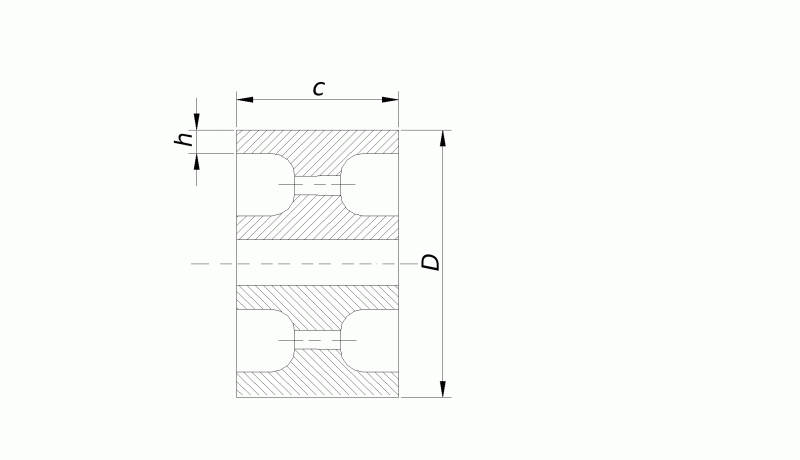
Определение момента инерции маховика:
 ;
;
Из последней формулы имеем
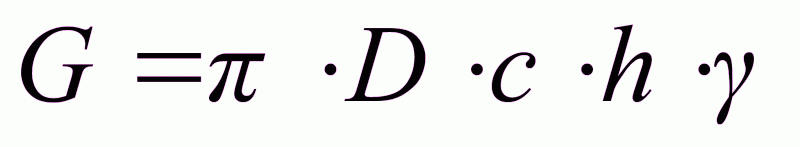
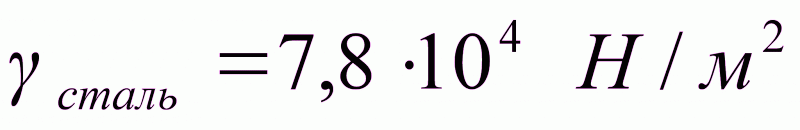
Принимаем D=1м.
h/c=1.2, тогда
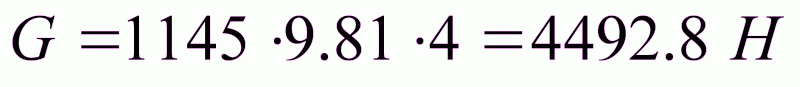
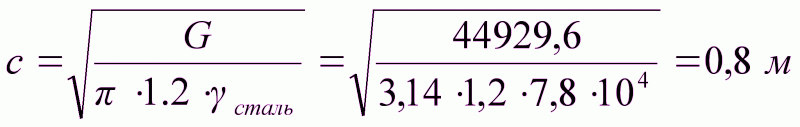
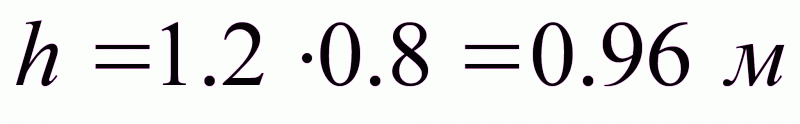
Определение истинных значений ускорений и скоростей кривошипа.
Для этого используем пакет MathCAD.



29-04-2015, 04:05
