Поделим обе части уравнения на Кdt. Получим следующее:
![]() (1)
(1)
где:
m - масса подаваемогоTiCl4 (кг);
с - теплоемкость TiCl4 (Дж/Кс) ;
Тk - температура в кубе-испарителе (К) ;
То.с. - температура окружающей среды (К) ;
N - мощность электронагревателей (кВт) ;
К - коэффициент теплоотдачи (Дж/Кс) .
Зная конструктивные размеры куба-испарителя производим необходимые расчеты:
Vк = 1,5 м3 m =Vк = 1730 1,5 = 2595 (кг) ,
где :
Vк - объем куба-испарителя ;
- плотность TiCl4 .
К=96923,25 Дж/Кс с = 747 Дж/Кс
Полученные данные подставим в уравнение (1).
Получим дифференциальное уравнение вида :
![]()
Решением данного дифференциального уравнения является функция:
![]()
![]() ,
где Т = 20,14
20 с .
,
где Т = 20,14
20 с .
Подставляя время получаем кривую разгона по каналу “мощность электронагревателей - количество испаренного TiCl4”.
Полученные данные приведены в таблице 5.2.2. По данным из таблицы 5.2.2. строим график кривой разгона по каналу “мощность электронагревателей - количество испаренного TiCl4”,приведенный на рисунке 5.2..4.
Таблица 5.2.2. Значения кривой разгона по каналу “мощность электронагревателей - количество испаренного TiCl4”.
-
Время
t,с
Значения
функции
Время
t,с
Значения
функции
0
0,00
35
0,83
5
0,22
40
0,86
10
0,39
45
0,89
15
0,53
50
0,92
20
0.63
55
0,94
25
0,71
60
0,95
30
0,78
65
0,96
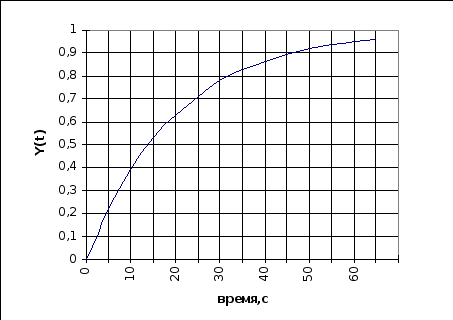
Рисунок 5.2.4. График кривой разгона по каналу “мощность электронагревателей - количество испаренного TiCl4”.
Рассчитываем кривую разгона по каналу “разность количеств подаваемого и испаренного TiCl4 - уровень в кубе-испарителе”.
Запишем уравнение изменения уровня в кубе-испарителе в дифференциальной форме :
F![]() = Qж - Qисп.
,
= Qж - Qисп.
,
где :
F - площадь зеркала испарения (м2) ;
![]() - скорость
изменения
уровня (м/с).
- скорость
изменения
уровня (м/с).
Площадь зеркала испарения F рассчитываем математически, зная конструктивные размеры куба-испарителя. Расчет ведется при заданном уровне 90 мм.
Длина куба-испарителя - 1,508 м. Ширину зеркала испарения при заданном уровне 90 мм рассчитываем геометрически. Схема расчета приведена на рисунке 5.2.5.

![]()
![]() б
б
![]()

![]()
![]()
![]()
![]()
![]()
Нк куба
![]()
![]()
![]()
![]()
![]()
Рисунок 5.2.5. Схема расчета ширины площади зеркала испарения.
Из расчета получается, что она равна 0,86 м. Следовательно площадь зеркала испарения равна :
F = l б = 1,508 0,86 = 1,75 м2.
Подставляем полученные данные в дифференциальное уравнение изменения уровня, при этом берем изменение количества TiCl4 равным 100 м3/ч.
1,75
![]() = 100
= 100
Получаем
дифференциальное
уравнение вида
![]() = 57,14.
= 57,14.
Решением данного дифференциального уравнения является функция вида :
Н = 57,14 t .
Подставляя время получаем кривую разгона по каналу “разность количеств подаваемого и испаренного TiCl4 - уровень в кубе-испарителе”.
Полученные данные приведены в таблице 5.2.3. По данным из таблицы 5.2.3. строим график кривой разгона по каналу “разность количеств подаваемого и испаренного TiCl4 - уровень в кубе-испарителе”, приведенный на рисунке 5.2.6.
Таблица 5.2.3. Значения кривой разгона по каналу “разность количеств подаваемого и испаренного TiCl4 - уровень в кубе-испарителе”.
-
Время
t,с
Значения
функции
Время
t,с
Значения
функции
0,00
0,00
1,25
71,42
0,25
14,29
1,50
85,71
0,50
28,57
1,75
100,00
0,75
42,86
2,00
114,28
1,00
57,14
2,10
119,90
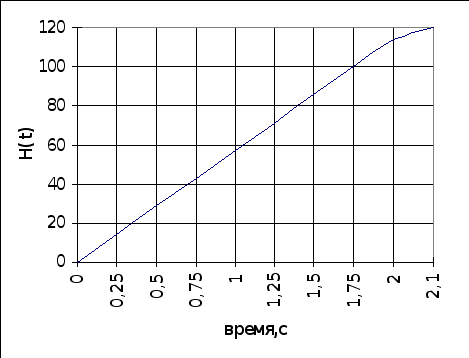
Рисунок 5.2.6. График кривой разгона по каналу “разность количеств подаваемого и испаренного TiCl4 - уровень в кубе-испарителе”.
6. РАСЧЕТНАЯ ЧАСТЬ
6.1. Аппроксимация переходных процессов.
6.1.1. Аппроксимация кривой переходного процесса объекта по каналу “положение регулирующего органа - расход TiCl4”
Определение передаточной функции объекта по основному каналу проводим по кривой разгона, полученной в разделе 5.2 проекта.
Значения точек кривой приведены в таблице 5.2.1, а график функции - на рисунке 5.2.2 .
Из графика переходного процесса видно, что этот объект обладает свойством самовыравнивания, потому расчёт передаточной функции будем проводить в программе Linreg .
Перед вводом точек кривой переходного процесса в программу, функции необходимо привести к безразмерному виду.
Это легко сделать в программе идентификации объектов управления, используя команду "нормировать".
Значения нормированной кривой приведены в таблице 6.1.1,
График нормированной кривой - на рисунке 6.1.1.
Таблица 6.1.1. Значения нормированной кривой по каналу “положение регулирующего органа - расход TiCl4”
-
Время
t,с
Значение функции
Время
t,с
Значение функции
0,0
0,0000
5,5
0,8477
0,5
0,0695
6,0
0,8874
1,0
0,1490
6,5
0,9161
1,5
0,2395
7,0
0,9360
2,0
0,3444
7,5
0,9492
2,5
0,4492
8,0
0,9603
3,0
0,5475
8,5
0,9702
3,5
0,6302
9,0
0,9801
4,0
0,6965
9,5
0,9901
4,5
0,7515
10,0
1,0000
5,0
0,8013
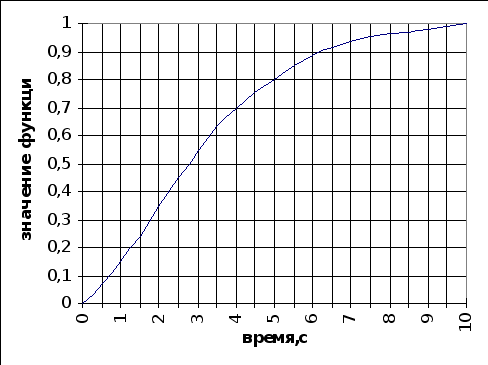
рис. 6.1.1. График нормированной кривой по каналу каналу “положение регулирующего клапана - расход TiCl4”.
После расчёта передаточной функции в Linreg получаем:
![]()
Коэффициент передачи объекта по каналу каналу “положение регулирующего органа - расход TiCl4” составляет:
Кпер. = (Х max. - Х0 )/ w ,
где :
Х max.- максимальное значение выходной величины, расход TiCl4 ;
Х0- начальное значение выходной величины, расход TiCl4 ;
w - величина внешнего возмущения, w = 10 %.
Кпер. = (600 - 500) / 10 = 10
6.1.2. Аппроксимация переходного процесса объекта по каналу “мощность электронагревателей - количество испаренного TiCl4”.
.
Аппроксимацию переходного процесса по каналу “мощность электронагревателей - количество испаренного TiCl4” проводим в той же последовательности, проведенной при аппроксимации переходного процесса по каналу “положение регулирующего органа - расход TiCl4”. Это связано с тем, что данный объект как и предыдущий имеет свойство самовыравнивания.
Значения нормированной кривой приведены в таблице 6.1.2.
График нормированной кривой изображен на рисунке 6.1.2.
Таблица 6.1.2. Значения нормированной кривой по каналу “мощность электронагревателей - количество испаренного TiCl4”.
-
Время
t,с
Значения
функции
Время
t,с
Значения
функции
0
0,0000
35
0,8564
5
0,2049
40
0,8949
10
0,3905
45
0,9264
15
0,5342
50
0,9545
20
0,6462
55
0,9755
25
0,7338
60
0,9895
30
0,8039
65
1,0000

рис. 6.1.2 График нормированной кривой по каналу каналу “мощность электронагревателей - количество испаренного TiCl4”.
Передаточная функция кривой разгона изображенной на рисунке 6.1.2. имеет вид :
![]()
Коэффициент передачи объекта по каналу “мощность электронагревателей - количество испаренного TiCl4” составляет:
Кпер. = ( Хmax - X0 )/ w
Кпер. = (0,96 - 0)/ 10 = 0.096
6.1.3. Аппроксимация переходного процесса по каналу “разность количеств подаваемого и испаренного TiCl4 - уровень в кубе-испарителе”.
Аппроксимацию переходного процесса по каналу “разность количеств подаваемого и испаренного TiCl4 - уровень в кубе-испарителе” проводить нет необходимости, так как кривая разгона по каналу “разность количеств подаваемого и испаренного TiCl4 - уровень в кубе-испарителе” представляет собой интегральную прямую (рисунок 5.2.6. раздела 5.2.).
6.2. Проверка аппроксимации переходных процессов.
6.2.1. Проверка аппроксимации переходного процесса по каналу “положение регулирующего органа - расход TiCl4”.
Проверку аппроксимации переходных процессов проводим с целью определения точности аппроксимации, путём получения переходного процесса "обратным путём". То есть - по полученным в разделе 6.1 передаточным функциям получаем кривую переходного процесса и сравниваем эту кривую с исходной. В идеальном случае - обе кривые должны совпасть.
Передаточная функция объекта по каналу “положение регулирующего органа - расход TiCl4”равна:
![]()
Для определения переходного процесса воспользуемся программой Aproc - нахождение уравнения реакции системы на ступенчатое возмущение методом Карсона-Хевисайда. После ввода в программу коэффициентов передаточной функции, получим следующее математическое выражение реакции системы на единичное ступенчатое воздействие y(t):
y(t) = 1 + 3,39 cos(4,46 - 0,15 t) e -0,59 t
Оформляем таблицу 6.2.1, в которой :
1 столбец - значения времени, с;
2 столбец - значения исходной кривой разгона, приведенной к безразмерной форме ;
Хнорм. - значения точек нормированной кривой, приведенных в таблице 6.1.1 ;
3 столбец - значения функции y(t) ;
4 столбец - абсолютная погрешность А, вычисленная по формуле:
А = Хнорм.(t) - y(t);
5 столбец - абсолютное значение разности квадратов Хнорм.(t) и y(t).
На рисунке 6.2.1 изображены исходная кривая переходного процесса и кривая, полученная преобразованием передаточной функции объекта (по данным столбцов 1 - 3 таблицы 6.2.1).
В 6 столбец записываем среднеквадратичное отклонение для двух функций, СКО = 0,007. Максимальная абсолютная погрешность составляет 3,16 %.
Таблица 6.2.1.
-
Время
t,c
Хнормир.
(t)
Y(t)
Абс.погреш-
ность
А
Разность квадратов
Х2норм.-Y2(t)
СКО
0,0
0,0000
0,0000
0,0000
0,0000
-0,0502
0,5
0,0695
0,0379
0,0316
0,0183
1,0
0,1490
0,1253
0,0255
0,0065
1,5
0,2395
0,2344
0,0051
0,0024
2,0
0,3444
0,3479
-0,0035
-0,0024
2,5
0,4492
0,4560
-0,0068
-0,0062
3,0
0,5475
0,5537
-0,0062
-0,0068
3,5
0,6302
0,6389
-0,0087
-0,0110
4,0
0,6965
0,7112
-0,0147
-0,0207
4,5
0,7517
0,7713
-0,0196
-0,0299
5,0
0,8013
0,8206
-0,0193
-0,0313
5,5
0,8477
0,8603
-0,0126
-0,0215
6,0
0,8874
0,8921
-0,0047
-0,0084
6,5
0,9161
0,9172
-0,0011
-0,0020
7,0
0,9360
0,9369
-0,0009
-0,0017
7,5
0,9492
0,9522
-0,0030
-0,0057
8,0
0,9603
0,9640
-0,0037
-0,0071
8,5
0,9702
0,9731
-0,0029
-0,0056
9,0
0,9801
0,9800
0,0001
-0,9410
9,5
0,9901
0,9852
0,0049
0,0195
10,0
1,0000
0,9881
0,0119
0,02370
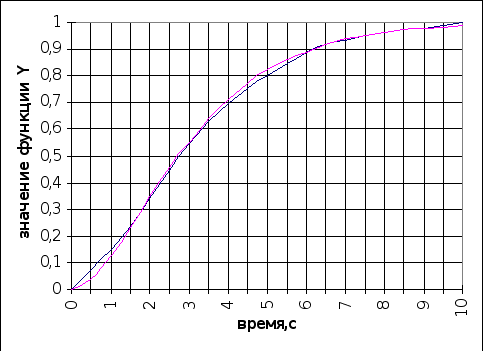
рис 6.2.1. Проверка аппроксимации переходного процесса по каналу “положение регулирующего органа - расход TiCl4”.
6.2.2. Проверка аппроксимации кривых переходного процесса по каналу “мощность электронагревателей - количество испаренного TiCl4” и каналу “разность количеств подаваемого и испаренного TiCl4 - уровень в кубе-испарителе”.
Проверку аппроксимации кривых переходного процесса по каналу “мощность электронагревателей - количество испаренного TiCl4” и каналу “разность количеств подаваемого и испаренного TiCl4 - уровень в кубе-испарителе” не производим, так как они были получены аналитически из математических зависимостей.
9. Построение математической модели и оптимизация технологического процесса.
Выбор критерия оптимальности.
Частной задачей вопроса автоматизации является оптимизация работы куба-испарителя, поэтому в задаче
6. РАСЧЕТНАЯ ЧАСТЬ
6.1. Аппроксимация переходных процессов.
6.1.1. Аппроксимация кривой переходного процесса объекта по основному каналу.
Определение передаточной функции объекта по основному каналу проводим по кривой разгона, полученной в разделе 5.2 проекта.
Значения точек кривой приведены в таблице 5.2.1, а график функции - на рисунке 5.2.1.
Так как исследуемый объект, как видно из графика переходного процесса, обладает свойством самовыравнивания, - расчёт передаточной функции будем проводить в программе Linreg . Перед вводом точек кривой переходного процесса в программу, функции необходимо привести к безразмерному виду. Это легко сделать в программе идентификации объектов управления , используя команду "нормировать". Значения нормированной кривой приведены в таблице 6.1.1, график нормированной кривой - на рисунке 6.1.1.
Таблица 6.1.1.
|
Время t,c. |
Значен. функц. |
Время t,c. |
Значен. функц. |
Время t,c. |
Значен. функц. |
Время t,c. |
Значен. функц. |
|
0 |
0 |
12 |
0,5293 |
24 |
0,904 |
36 |
0,9847 |
|
1 |
0 |
13 |
0,5763 |
25 |
0,9173 |
37 |
0,9867 |
|
2 |
0,0017 |
14 |
0,624 |
26 |
0,931 |
38 |
0,9883 |
|
3 |
0,0167 |
15 |
0,6687 |
27 |
0,9393 |
39 |
0,992 |
|
4 |
0,0467 |
16 |
0,709 |
28 |
0,947 |
40 |
0,994 |
|
5 |
0,0933 |
17 |
0,7457 |
29 |
0,9533 |
41 |
0,996 |
|
6 |
0,1433 |
18 |
0,7787 |
30 |
0,9597 |
42 |
0,9963 |
|
7 |
0,2083 |
19 |
0,808 |
31 |
0,9653 |
43 |
0,9967 |
|
8 |
0,277 |
20 |
0,8297 |
32 |
0,9707 |
44 |
0,9977 |
|
9 |
0,346 |
21 |
0,8517 |
33 |
0,976 |
45 |
1,000 |
|
10 |
0,411 |
22 |
0,8723 |
34 |
0,98 |
46 |
|
|
11 |
0,4713 |
23 |
0,889 |
35 |
0,983 |
47 |
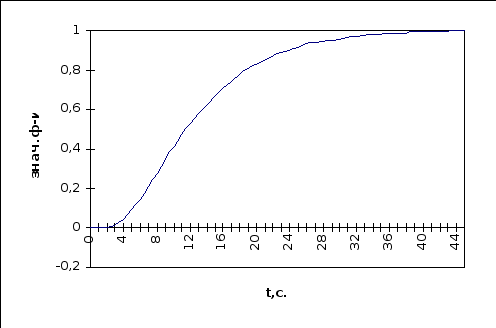
рис. 6.1.1. График нормированной кривой по основному каналу
После расчёта передаточной функции в Linreg получаем:
![]()
Коэффициент передачи объекта по основному каналу составляет:
Кв.к. = (Х max. - Х0 )/ w , где
Х max.- максимальное значение выходной величины, рН;
Х0- начальное значение выходной величины, рН;
w - величина внешнего возмущения, w = 10 %.
Кв.к. = (12.05 - 2.05) / 10 = 1,0
6.1.2. Аппроксимация переходного процесса объекта по внутреннему каналу .
Аппроксимацию переходного процесса по внутреннему каналу проводим в последовательности, проведенной при аппроксимации переходного процесса по основному каналу, так как оба объекта имеют свойство самовыравнивания.
Значения нормированной кривой приведены в таблице 6.1.2. График нормированной кривой на рисунке 6.1.2.
Таблица 6.1.2.
|
Время t,c |
Значение функции |
|
0 |
0,000 |
|
1 |
0.0256 |
|
2 |
0,0513 |
|
3 |
0,0798 |
|
4 |
0,1311 |
|
5 |
0,2194 |
|
6 |
0,3476 |
|
7 |
0,4786 |
|
8 |
0,5983 |
|
9 |
0,698 |
|
10 |
0,8006 |
|
11 |
0,8989 |
|
12 |
0,9993 |
|
13 |
1,000 |
После расчета передаточной функции в Linreg получаем передаточную функцию следующего вида:
![]()
Коэффициент передачи по внутреннему каналу составляет:
Кпер. = ( Хmax - X0 )/ w
Кпер. = ( 3.9 - 2.05 )/ 10 = 0.145

рис. 6.1.2 График нормированной кривой по внутреннему каналу
6.1.3. Аппроксимация переходного процесса по каналу внешнего возмущения.
Также по аналогии проводим аппроксимацию переходного процесса по каналу внешнего возмущения. Значение функции нормированной кривой заносятся в программу Linreg, после чего производится расчет передаточной функции объекта по каналу внешнего возмущения. Значения функций заносим в таблицу 6.1.3. График нормированной кривой по каналу внешнего возмущения на рисунке 6.1.3.
Таблица 6.1.3.
|
Время с. |
Значен. функц. |
Время с. |
Значен. функц. |
Время с. |
Значен. функц. |
Время с. |
Значен. функц. |
|
0 |
0,001 |
10 |
0,3131 |
20 |
0,6762 |
30 |
0,9162 |
|
1 |
0,0095 |
11 |
0,3486 |
21 |
0,7067 |
31 |
0,9314 |
|
2 |
0,019 |
12 |
0,3867 |
22 |
0,7371 |
32 |
0,9467 |
|
3 |
0,04 |
13 |
0,4267 |
23 |
0,7676 |
33 |
0,9619 |
|
4 |
0,0743 |
14 |
0,4686 |
24 |
0,7905 |
34 |
0,9771 |
|
5 |
0,1162 |
15 |
0,5105 |
25 |
0,8133 |
35 |
0,9867 |
|
6 |
0,1543 |
16 |
0,5467 |
26 |
0,8362 |
36 |
0,9924 |
|
7 |
0,1886 |
17 |
0,581 |
27 |
0,861 |
37 |
0,9962 |
|
8 |
0,2293 |
18 |
0,6114 |
28 |
0,88 |
38 |
0,9981 |
|
9 |
0,2712 |
19 |
0,6457 |
29 |
0,899 |
39 |
1,000 |
После проведения расчета передаточной функции получаем передаточную функцию следующего вида:
![]()
Коэффициент передачи в данном случае будет равен:
Кпер.= (12,7-3,95)/8,75=1

рис.6.1.3. График нормированной кривой по каналу внешнего возмущения
6.2. Проверка аппроксимации переходных процессов.
6.2.1. Проверка аппроксимации переходного процесса по основному каналу.
Проверку аппроксимации переходных процессов проводим с целью определения точности аппроксимации, путём получения переходного процесса "обратным путём". То есть - по полученным в разделе 6.1 передаточным функциям получаем кривую переходного процесса и сравниваем эту кривую с исходной. В идеальном случае - обе кривые должны совпасть.
Передаточная функция объекта по основному каналу равна:
![]()
Для определения переходного процесса воспользуемся программой Aproc - нахождение уравнения реакции системы на ступенчатое возмущение методом Карсона-Хевисайда. После ввода в программу коэффициентов передаточной функции, получим следующее математическое выражение
реакции системы на единичное ступенчатое воздействие y(t):
y(t) = 1 + 1.89 * Cos(4,15 - 0,07 * t) * exp(-0,11 * t).
Оформляем таблицу 6.2.1, в которой :
1 столбец - значения времени, с.
2 столбец - значения исходной кривой разгона, приведенной к безразмерной форме.
Хнорм. - значения точек нормированной кривой, приведенных в таблице 6.1.1
3 столбец - значения функции y(t)
4 столбец - абсолютная погрешность А, вычисленная по формуле:
А = Хнорм.(t) - y(t);
5 столбец - абсолютное значение разности квадратов Хнорм.(t) и y(t).
На рисунке 6.2.1 изображены исходная кривая переходного процесса и кривая, полученная преобразованием передаточной функции объекта (по данным столбцов 1 - 3 таблицы 6.2.1).
В 6 столбец записываем среднеквадратичное отклонение для двух функций, СКО = 0,007. Максимальная абсолютная погрешность составляет 2,4%.
Таблица 6.2.1.
|
Время t,с |
Хнормир.(t) |
Y(t) |
Абс.погрешн-ть А |
Раз-ть квадратов Х2норм.-Y2(t) |
СКО |
|
0 |
0.000 |
0.000 |
0.000 |
0.000 |
0.007 |
|
1 |
0.000 |
0.0078 |
-0.0078 |
0.000 |
|
|
2 |
0.0017 |
0.011 |
0.006 |
0.000 |
|
|
3 |
0.0167 |
0.027 |
0.014 |
0.0005 |
|
|
4 |
0.0467 |
0.059 |
-0.0123 |
0.001 |
|
|
5 |
0.0933 |
0.101 |
-0.0077 |
0.002 |
|
|
6 |
0.1433 |
0.165 |
-0.0217 |
0.006 |
|
|
7 |
0.2083 |
0.233 |
-0.0247 |
0.01 |
|
|
8 |
0.277 |
0.2988 |
-0.0218 |
0.012 |
|
|
9 |
0.346 |
0.3517 |
-0.0057 |
0.004 |
|
|
10 |
0.411 |
0.4039 |
0.01 |
0.005 |
|
|
11 |
0.4713 |
0.4548 |
0.019 |
0.01 |
|
|
12 |
0.5293 |
0.5038 |
0.02 |
0.02 |
|
|
13 |
0.5763 |
0.574 |
0.002 |
0.003 |
|
|
14 |
0.624 |
0.619 |
0.005 |
0.006 |
|
|
15 |
0.6687 |
0.666 |
0.002 |
0.004 |
|
|
16 |
0.709 |
0.7117 |
-0.002 |
0.004 |
|
|
17 |
0.7457 |
0.745 |
0.0007 |
0.001 |
|
|
18 |
0.7787 |
0.7756 |
0.003 |
0.004 |
|
|
19 |
0.808 |
0.8036 |
0.005 |
0.007 |
|
|
20 |
0.8297 |
0.8289 |
0.0006 |
0.001 |
|
|
21 |
0.8517 |
0.8519 |
-0.0002 |
0.0001 |
|
|
22 |
0.8723 |
0.8725 |
-0.0002 |
0.0001 |
|
|
23 |
0.889 |
0.887 |
0.002 |
0.003 |
|
|
24 |
0.904 |
0.911 |
-0.007 |
0.01 |
|
|
25 |
0.9173 |
0.920 |
-0.003 |
0.005 |
|
|
26 |
0.931 |
0.934 |
-0.003 |
0.005 |
|
|
27 |
0.9393 |
0.935 |
0.004 |
0.008 |
|
|
28 |
0.947 |
0.9463 |
0.001 |
0.001 |
|
|
29 |
0.9533 |
0.9562 |
-0.002 |
0.005 |
|
|
30 |
0.9597 |
0.9648 |
-0.005 |
0.01 |
|
|
31 |
0.9653 |
0.9723 |
-0.007 |
0.01 |
|
|
32 |
0.9707 |
0.9787 |
-0.008 |
0.01 |
|
|
33 |
0.976 |
0.9841 |
-0.008 |
0.01 |
|
|
34 |
0.98 |
0.9887 |
-0.008 |
0.01 |
|
|
35 |
0.983 |
0.9926 |
-0.009 |
0.008 |
|
|
36 |
0.9847 |
0.9958 |
-0.011 |
0.02 |
|
|
37 |
0.9867 |
0.9985 |
-0.012 |
0.01 |
|
|
38 |
0.9883 |
1.0006 |
-0.012 |
0.009 |
|
|
39 |
0.992 |
1.0023 |
-0.01 |
0.01 |
|
|
40 |
0.994 |
1.0037 |
-0.009 |
0.01 |
|
|
41 |
0.996 |
1.0047 |
-0.008 |
0.009 |
|
|
42 |
0.9963 |
1.0054 |
-0.009 |
0.01 |
|
|
43 |
0.9967 |
1.006 |
-0.009 |
0.01 |
|
|
44 |
0.9977 |
1.0063 |
-0.002 |
0.01 |
|
|
45 |
1.000 |
1.0065 |
-0.0065 |
0.01 |
|
|
Сумма |
0.3327 |
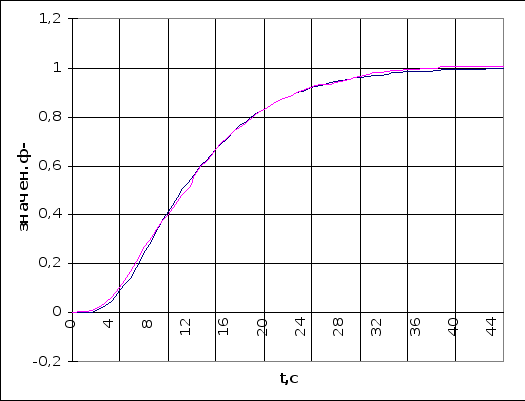
рис 6.2.1. Проверка аппроксимации переходного процесса по основному каналу.
6.2.2. Проверка аппроксимации кривой переходного процесса по внутреннему каналу.
Для получения математического выражения реакции внутреннего канала на единичное воздействие воспользуемся программой Aproc. Передаточная функция объекта по внутреннему каналу имеет вид:
![]()
Вводим в программу коэффициенты передаточной функции и после расчёта получаем следующее выражение реакции внутреннего канала на единичное ступенчатое воздействие:
y(t) = 1 + 1,57 * Cos(4,02 - 0,14 * t) * exp(-0,17 * t).
Далее, аналогично таблице 6.2.1 оформляем таблицу 6.2.2. Значения столбцов 1, 2 заполняем в соответствии с таблицей 6.1.2.
По значениям первых трёх столбцов строим исходную кривую переходного процесса, а так же кривую полученную путём перехода к оригиналу по Карсону-Хевисайду (рисунок 6.2.2).
29-04-2015, 03:59
