НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ
“КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ”
Славінська Олена Сергіївна
УДК 532.5:627.13
МОДЕЛІ ТА МЕТОДИ РОЗРАХУНКУ ВНУТРІШНІХ ТЕЧІЙ З УРАХУВАННЯМ АНІЗОТРОПІЇ ВІДКРИТИХ ТУРБУЛЕНТНИХ ПОТОКІВ
01.02.05. - механіка рідини, газу та плазми
Автореферат
дисертації на здобуття наукового ступеня
кандидата технічних наук
Київ - 2000
Дисертацією є рукопис.
Робота виконана на кафедрі будівництва та експлуатації доріг
Українського транспортного університету
Міністерства освіти та науки України.
Науковий керівник:
Доктор технічних наук, професор
Савенко В'ячеслав Якович,
Український транспортний університет,
завідуючий кафедрою будівництва та експлуатації доріг,
декан дорожньо-будівельного факультету
Офіційні опоненти:
Доктор технічних наук, старший науковий співробітник
Ткачук Сергій Григорович,
Київський національний університет культури та мистецтв,
професор кафедри інформатики
Кандидат технічних наук, доцент
Щодро Олексій Євгенович,
Рівненський державний технічний університет,
доцент кафедри гідротехнічних споруд
Провідна установа:
Інститут гідромеханіки Національної академії наук України, м. Київ
Захист відбудеться “19” червня 2000 р. о 15 годині на засіданні спеціалізованої вченої ради Д 26.002.09 при Національному технічному університеті України “Київський політехнічний інститут” 03056, м. Київ, пр. Перемоги 37, за адресою: м. Київ, вул. Політехнічна, 6, корпус 5, аудиторія 307.
З дисертацією можна ознайомитися в бібліотеці Національного технічного університету України “Київський політехнічний інститут” за адресою 03056, м. Київ, пр. Перемоги 37.
Автореферат розісланий “19” травня 2000 р.
Вчений секретар
спеціалізованої вченої ради В.І. Коньшин
Загальна характеристика роботи
Актуальність теми. Швидкий розвиток обчислювальної гідродинаміки викликаний її широким впровадженням у практику інженерного проектування. При проектуванні різноманітного роду гідротехнічних споруд необхідно вибрати найбільш ефективний режим їхньої роботи. Така складна задача потребує урахування цілого ряду особливостей турбулентної течії, що переважає у відкритому водяному потоці, анізотропні властивості якого багато в чому визначають розвиток внутрішніх течій. Механізм цього явища пояснюється взаємодією турбулентного потоку з твердими границями у природних та штучно стиснутих руслах - стрибкоподібною зміною глибини, різнорідністю шорсткостей по периметру живих перетинів, та наявністю штучних споруд.
Загальновідомо, що існують два види вторинних течій: перший - обумовлений наявністю відцентрових сил інерції; другий - неоднорідністю розподілу турбулентних напруг по живому перетину потоку. Що стосується течій першого виду, то можна стверджувати, що на сьогоднішній день ця проблема достатньо досліджена і може певним чином удосконавлюватись, а те, що стосується другого виду течій – необхідно відмітити про наявність обмеженої кількості робіт і недостатність вивченості цього явища.
Дослідження відкритих водоймищ на підставі тривимірних рівнянь турбулентного руху рідини свідчать про просторовий характер течій в них, який являє собою накладення на основний плин вихорів поперечної циркуляції. Наявність таких вихорів призводить до перерозподілу швидкостей по вертикалі і ширині потоку; зміни транспортуючої здатності його, і як наслідок, до небажаних деформацій русел; появи значних градієнтів тиску, і в кінцевому результаті, до зміни всієї швидкісної його структури. Внутрішні течії (вторинні течії поперечної циркуляції) та анізотропний стан турбулентного потоку – два взаємопов'язаних явища, які обумовлюють: однопорядковість трьох компонентів швидкості в певних часових та просторових полях, і як наслідок, перерозподіл дотичних напруг; турбулентних напруг; стрибкоподібну зміну швидкості дисипації кінетичної енергії турбулентності. Тому розробка методу розрахунку внутрішніх течій у просторовому турбулентному потоці є актуальною задачею, що становить науковий і практичний інтерес.
Зв'язок роботи з науковими програмами, планами, темами. Робота виконана відповідно до координаційного плану №24 межвузівскої науково-технічної програми на 1997-1999 рік по спеціальному напрямку “Автомобільний транспорт та дорожнє будівництво” Міністерства освіти та науки України “Теоретичні основи удосконалення ефективного функціонування дорожньо-будівельного комплексу України в умовах ринкової економіки”.
Мета і задачі дослідження. Розробити метод розрахунку внутрішніх течій з урахуванням анізотропного стану тривимірного турбулентного потоку на основі фізичної та математичної моделей механізму цих течій.
1. Обгрунтувати фізичну модель механізму внутрішніх течій та на її основі отримати гідродинамічний опис при узгодженості з полем тиску.
2. Узагальнити та пристосувати замикаючу модель турбулентності, яка базується на алгебраїчних співвідношеннях переносу напруг Рейнольдса та рівняннях 
моделі.
3. Обгрунтувати вибір та сформулювати початкові і граничні умови для розв'язування рівнянь запропонованих математичної моделі внутрішніх течій та замикаючої моделі турбулентності.
4. Розробити метод реалізації запропонованих математичних моделей внутрішніх течій та турбулентності.
5. З метою апробації розроблених математичних моделей і методів її реалізації, провести експериментальні дослідження гідродинамічної структури турбулентного потоку при наявності факторів анізотропного стану.
Наукова новизна одержаних результатів.
1. Розроблено математичну модель механізму внутрішніх течій при узгодженні тривимірного швидкісного поля з полем гідродинамічного тиску.
2. Вперше запропоновано анізотропний стан відкритого турбулентного потоку враховувати за допомогою алгебраїчних співвідношень переносу напруг Рейнольдса та двопараметричної моделі турбулентності.
3. Розроблено методику чисельної реалізації математичної моделі механізму внутрішніх течій у річищах довільного об'єму.
4. За допомогою чисельного та лабораторного експериментів проведено аналіз анізотропного стану відкритих русел, для яких найбільш характерні внутрішні течії.
Достовірність наукових висновків і рекомендацій підтверджується теоретичними розробками, що базуються на фундаментальних положеннях гідромеханіки, збіжністю розрахункових та експериментальних даних, відповідністю прогнозованого і фактичного результатів розвитку внутрішніх течій при анізотропному стані турбулентного середовища.
Практичне значення одержаних результатів полягає в тому, що вони дозволяють: підвищити науково-інженерний рівень розв'язування народногосподарської задачі взаємодії відкритих водних потоків із гідротехнічними об'єктами; забезпечити коректні розрахункові значення швидкісного поля відкритого потоку для оцінки руслових деформацій; замінити фізичне моделювання явищ та процесів математичними; розв'язувати задачі досліджень екологічних проблем поширення забруднюючих речовин у відкритих водоймищах.
Результати досліджень знайшли практичне втілення при виконанні технічного проекту мостового переходу через річку Західний Буг біля с. Ягодин, який розробляється проектним інститутом “Укрдіпродор”, та проекту реконструкції мостового переходу – дамби через р. Південний Буг біля смт Летичів, який розробляється науково-виробничою фірмою “Мостбудсервіс”, що підтверджується довідками про впровадження.
Особистий внесок здобувача в отриманні наукових результатів, викладених у дисертаційній роботі, полягає в:
· обгрунтуванні фізичної моделі механізму внутрішніх течій та розробки на її основі математичної моделі з урахуванням анізотропного стану турбулентного відкритого потоку;
· розробці методу реалізації запропонованих математичних моделей на підставі сучасних обчислювальних методів газогідродінаміки з використанням ефективних чисельних алгоритмів;
· проведенні та аналізу експериментальних досліджень гідродинамічної структури потоку в штучно стиснутому руслі.
Апробація результатів дисертації. Основні результати досліджень доповідалися і обговорювалися на щорічних наукових конференціях професорсько-викладацького складу Українського транспортного університету (1995-1999 р.); науково-технічній конференції “Гидромеханика в инженерной практике” (27 - 30 травня, 1996, м. Київ); II Республіканській науково-технічній конференції “Гидроаэромеханика в инженерной практике” (27 - 30 травня, 1997, м. Черкаси); сесії-конференції Транспортної Академії України, Західного наукового центру (Одеса – Львів, 28-31 травня 1998 р.); Міжнародній науково-технічній конференції “Гидравлика и гидрология транспортних сооружений. Автомобильные дороги и аєродроми” (м. Саратов, 1997 р.); науково-технічній конференції “Гидроаэромеханика в инженерной практике” (2 - 5 червня, 1999, м. Суми); засіданні Українського наукового семінару з гідравліки при Українському транспортному університеті (27 квітня 1999 р.).
Публікації. По темі дисертації опубліковано 11 наукових праць із них: 7 статей в спеціалізованих виданнях, 4 – в матеріалах конференцій (1 доповідь, 3 тези).
Структура й обсяг роботи. Дисертація складається із вступу, чотирьох розділів, висновків, списку літератури з 116 найменувань на 9 сторінках та 5 додатків на 35 сторінках. Робота містить 133 сторінок основного тексту, на яких 29 рисунків і 1 таблиця. Прикладено довідки про впровадження результатів досліджень в практику проектування мостових переходів.
Користуючись нагодою хочу висловити щиру подяку за допомогу та підтримку при виконанні дисертаційної роботи своєму другому науковому керівникові, заслуженому діячу науки і техніки України, лауреату Державної премії України, завідуючому кафедри мостів та тунелей Українського транспортного університету, доктору технічних наук, професору Большакову Валерію Олексійовичу, який був призначеним науковим керівником наказом № 255 по Українському транспортному університету від 15 листопада 1995 р.
Основний зміст роботи
У вступі обгрунтовано доцільність та актуальність теми дисертаційної роботи, її зв'язок з науковими програмами, мета, наукова новизна та практичне значення. У вступі також розкривається особистий внесок автора, питання апробації результатів, публікації, загальний обсяг і структура роботи.
У першому розділі дається стислий огляд методів розв'язування поставленої задачі, яка подана у подвійному аспекті. З одного боку розглядаються основні методи розрахунку внутрішніх течій, а саме складових швидкості, для одновимірних і двовимірних потоків. З іншого - дається огляд основних моделей турбулентності, за допомогою яких вирішується проблема замикання основних рівнянь гідродинаміки. Що стосується внутрішніх течій, то можна перерахувати достатньо велику кількість учених, які займаються і вносили серйозний внесок у рішення даної наукової проблеми: В.М. Маккавеєв, А.К. Ананян, І.Л. Розовський, І.А. Шеренков, В.Я. Савенко та ін. Розглядаючи другий аспект, необхідно зазначити таких провідних вчених, як Б.Є. Лаундер, В. Роді, П. Бредшоу, І.А. Бєлов, Є.В. Бруяцький, А.П. Нетюхайло, Є.П. Дибан, Е.Я. Епік. На підставі наведеного аналізу, зроблені висновки по стану питання про розв'язування проблеми внутрішніх течій у відкритому потоці.
В другому розділі обгрунтована фізична модель механізму внутрішніх течій на підставі опрацювання й аналізу експериментальних даних по задачі, яка розглядається з урахуванням анізотропного стану турбулентного потоку. Результати обробки експериментів, які подані на рис. 1, представлені полями ізотах у живому перетині потоку прямолінійного русла з різнорідною шорсткістю дна. Збільшення кривизни ізотахи призводить до підвищення інтенсивності внутрішніх течій, і як наслідок до зміни розподілу внутрішніх турбулентних напруг, що підтверджує їх тісний взаємозв'язок.
Фізична модель механізму внутрішніх течій з урахуванням анізотропної природи турбулентності дозволяє розробити математичну модель цих течій за загальноприйнятою схемою досліджень, яка запропонована І.А. Шеренковим та В.Я. Савенко. Такий підхід чітко обгрунтовується методами кінематики твердого тіла, що одночасно бере участь у двох рухах: поступальному та обертальному.
Якщо розглядати течії без архімедових сил, то можна прийти до висновку, що внутрішні течії виникають внаслідок процесів, які обумовлені трьома взаємопов'язаними причинами: перша - вторинні течії формуються під дією відцентрових сил інерції; друга – (за В. Роді), за рахунок нерівності компонент нормальних турбулентних напруг; третя (за Н. А. Картвелішвілі) - за рахунок нерівномірності розподілу дотичних напруг.
Для аналізу турбулентного потоку, зокрема його тривимірних ефектів, за вихідні прийняті диференціальні рівняння осередненого турбулентного руху і нерозривності. Особливістю цих рівнянь є наявність тензора напруг Рейнольдса, за допомогою яких можна описати механізм внутрішніх течій.
При розробці тривимірної моделі механізму внутрішніх течій локальну швидкість 
представляємо у загальноприйнятому вигляді, як суму осередненої на вертикалі 
та швидкості внутрішніх течій 
:
(1)
Нерівномірність розподілу швидкостей по вертикалі враховується за допомогою коефіцієнта 
та степеневого закону розподілу швидкостей по вертикалі (як найбільш відповідного до реальних умов):
(2)
На підставі аналізу результатів досліджень І.А. Шеренкова та В.Я. Савенка локальні швидкості на вертикалі представляються у вигляді співвідношень:
(3)
Посилаючись на наведені вище положення, що до процесу утворення внутрішніх течій, в модельному рівнянні поряд з турбулентними напругами 
ураховуються дотичні напруги 
, які обумовлені наявністю внутрішніх течій. Дотримуючись умов спрощення, отримана наступна модельна форма рівнянь:
(4)
(5)
(6)
(7)
Для складової швидкості внутрішніх течій 
отримане рівняння у вигляді:
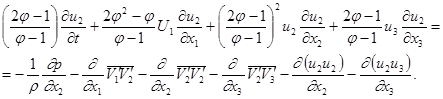(8)
Для врахування деформацій вільної поверхні потоку, які зумовлені наявністю значних градієнтів тиску в області розв'язування задачі, запропоновано рівняння:
(9)
де 
- глибина потоку на вертикалі.
Завершальний етап розрахунку швидкісного поля потребує перевірки виконання рівняння нерозривності. В разі його невиконання запропоновано ввести потенційну поправку 
, яка обумовлюється градієнтом повздовжньої швидкості 
. Малий порядок цієї поправки дозволяє не включати її до рівняння нерозривності, а використовувати лише для корекції швидкісного поля, яка врахована в алгоритмі розв'язування задачі, а математичний опис її має вигляд:
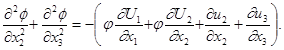(10)
При чисельному моделюванні тривимірних ефектів у товщі турбулентного потоку для замикання математичного опису механізму внутрішніх течій застосовується модифікована модель, яка складається з рівнянь переносу кінетичної енергії та швидкості її дисипації, що отримані з рівнянь гідродинаміки і мають свою фізичну інтерпретацію:
(11)
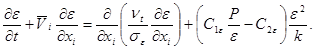(12)
Генерація кінетичної енергії 
визначається за формулою:
(13)
Модифікована модель цілком оптимальна для внутрішніх течій за анізотропного коефіцієнту турбулентної в'язкості 
, при її спільному використані з алгебраїчною моделлю переносу напруг Рейнольдса. Застосування алгебраїчних виразів переносу турбулентних напруг більш широко розкривають природу турбулентності та враховують її анізотропний стан. Ці вирази отримані з повних рівнянь переносу турбулентних напруг шляхом введення модельних співвідношень та їх спрощення. Алгебраїчні вирази можуть бути представлені у вигляді:
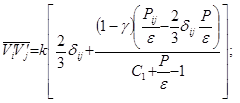(14)
(15)
де 
- член генерації турбулентності, який характеризує перенос енергії від осередненої течії до пульсуючої;
або
- індекси, які визначають напрямок декартової системи координат;
- символ Кронекера (
при 
та 
при 
).
Коефіцієнт турбулентної в'язкості визначається по співвідношенню Колмогорова – Прандтля, яке використовується в двопараметричних моделях:
(16)
За показник, що характеризує анізотропний стан турбулентного потоку використовується тензор анізотропії 
, або девіатор тензора напруг, який дорівнює нулю для ізотропного поля та визначається співвідношенням:
(17)
Для забезпечення адекватного опису характеристик осередненої течії і турбулентності у тривимірному потоці, при наявності внутрішніх течій, залежність для величини 
визначається як функція відношення генерації кінетичної енергії до швидкості дисипації 
:
(18)
При реалізації розглядуваної задачі суттєвим є питання узгодженості розподілу швидкостей і поля гідродинамічного тиску, для опису якого запропоновано рівняння у вигляді рівняння Пуассона:
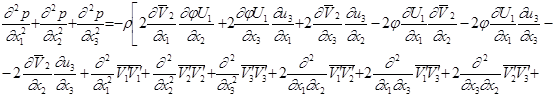
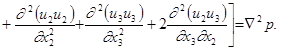(19)
Запропоновані математичні моделі механізму внутрішніх течій дозволяють у новому аспекті розв'язувати задачу розрахунку цих течій.
У третьому розділі наведено методи реалізації запропонованих математичних моделей, представлених у фізичних координатах. Область розв'язування являє собою тривимірний простір зі змінними границями. Для універсалізації та спрощення алгоритму пропонується перейти до безрозмірних координат у області зі сталими границями.
У випадку безнапірного потоку довжиною 
(
) із поперечним перетином довільної форми система координат 
заміняється “новою” системою координат 
- 
при цьому:
(20)
де 
- відмітки, відповідно, дна та берега русла від початку декартової системи координат.
Такий підхід дозволяє отримати рівномірну сітку в обчислювальній області, хоча вузли сітки у фізичному просторі можуть бути розташовані нерівномірно. При переході до “нових” координат у диференціальні рівняння вводяться матричні коефіцієнти перетворення.
Для реалізації дискретних аналогів рівнянь внутрішніх течій (4) – (6), (8), (9) та моделі турбулентності (11) – (12) використовується скінченнорізницевий метод типу предиктор - коректор по явній схемі Мак-Кормака, з розщепленням диференціальних рівнянь на одновимірні за просторовими координатами та часом. Використання явної модифікованої схеми Мак-Кормака, типу предиктор - коректор, обгрунтовується її гнучкістю, що дозволяє нестаціонарну тривимірну задачу звести до послідовного розв'язування одномірних маршових задач і створювати різноманітні модифікації в умовах накладення нерівномірної сітки на примежові зони потоку та великих чисел Рейнольдса; стійкістю при виконанні умови Куранта – Фрідріха – Леві; узгодженістю при співпаданні суми кроків для кожного скінченнорізницевого оператора та отриманні другого порядку точності результатів за першого порядку апроксимації вихідних операторів. У безнапірних змінних скорочений запис схеми має вигляд:
(21)
де 
Для раціонального використання явної схеми Мак-Кормака за великих чисел Рейнольдса 
і для врахування впливу граничних умов на основний турбулентний потік, розв'язування ведеться за схемою у вигляді
29-04-2015, 00:29