На законі Паскаля ґрунтується принцип дії різноманітних гідравлічних пристроїв, за допомогою яких тиск передається на відстань /гідравлічний прес, гідравлічний домкрат, гідромультиплікатор та інші./

2.5 Сила тиску рідини на плоску стінку. Центр тиску

Визначимо силу тиску рідини на площину ω плоскої стінки, яка розташована під довільним кутом до горизонту. Розв’язання задачі зручно проводити в системі координат хОу, вісь Оу якої напрямлена вздовж стінки, а вісь Ох співпадає з лінією перетину стінки і вільної поверхні рідини. Для зручності вісь Ох повернута на кут 90⁰ , (рис.2.6).

Очевидно що між будь – якою координатою у і глибиною занурення h існує зв’язок:

Сила тиску dР на довільну елементарну площину dω

де р_о – тиск на вільній поверхні рідини густиною ρ.

Повна сила тиску на площину w стінки:

^* )

Рис. 2.6

Для зручності вісь Ох повернута на кут 90^о

Інтеграл є статичним моментом площини W відносно осі Ох, величина якого дорівнює добутку ω на відстань її центра ваги до осі Ох тобто

Тоді

(2.16)

де h_с – глибина занурення центра ваги стінки площиною ω. Сила тиску самої рідини без урахування зовнішнього тиску p.

(2.17)

У випадку, коли плоска стінка горизонтальна і розміщена на глибині h ,то h_c =h і

(2.18)

Якщо плоска стінка вертикальна α=90^о і h_c =y_c .

Досить часто в інженерних розрахунках важливо не тільки визначити величину сили тиску рідини, але й знайти точку прикладення її рівнодіючої – так званий центр тиску.

Для цього користуться теоремою Варіньйона: момент рівнодіючої сили дорівнює алгебраїчній сумі моментів сладових її. Відповідно до рис.2,6 можна записати

де у_d – координата центра тиску , Р=Р_над – сила тиску рідини.

Тоді

(2.19)

Тут – момент інерції змоченої площини ω відносно осі Ох ; у_с ω – статичний момент цієї площини.

На підставі теореми про моменти інерції відносно паралельних осей /теорема Гюйгенса/

де I_c – момент інерції плоскої фігури відносно осі, що проходить через її центр ваги паралельно осі Ох, тому залежності (2.19) можна надати вигляду

.

(2.20)

2.6 Сила тиску рідини на криволінійні поверхні

Визначення сили сумарного тиску рідини на поверхні довільної форми в загальному випадку зводиться до визначення трьох складових цієї сили і трьох моментів /в системі координат Оху/

В техніці переважно мають справу з циліндричними або сферичними поверхнями, які мають вертикальну площину симетрії.

Розглянемо посудину з боковою стінкою циліндричної форми, котра заповнена рідиною, на вільну поверхню якої діє тиск р₀ і визначимо силу тиску на ділянку АВ цієї стінки в двох випадках:

1) рідина знаходиться над стінкою (рис.2.7а);

2) рідина знаходиться під стінкою. (рис.2.7б).

a), б)

Рис.2.7

В першому випадку виділимо об’єм АВСD рідини, обмежений ділянкою АВ стінки, вертикальними поверхнями АD і ВС, що проведені через границі цієї ділянки, і вільною поверхнею рідини. Сумарну силу тиску Р на ділянку АВ розкладемо на дві складові: вертикальну Р_В і горизонтальну Р_Г. З умови рівноваги об’єму АВСD у вертикальному напрямі знаходимо що

,

(2.21)

Де G- вага виділеного об’єму рідини; ω_Г – площа проекції поверхні АВ на горизонталь.

В свою чергу сила ваги . Об’єм рідини, що міститься в геометричній фігурі АВСD часто називають “тілом тиску” і позначають через V_тт . З урахуванням цього рівняння (2.21) запишеться у формі

.

(2.22)

При визначенні горизонтальної складової сили тиску на поверхню АВ потрібно урахувати, що сили тиску на поверхні ВС і DЕ взаємно зрівноважуються. Тоді

.

(2.23)

В останньому рівнянні h_c – заглиблення центра ваги (мас) вертикальної проекції поверхні АВ – ω_в

Очевидно, що повна сила тиску на циліндричну поверхню

.

(2.23)

Коли рідина розташована під стінкою рис.2.7б складові Р_в і Р_г також визначаються формулами 2.21 або 2.22 і 2.23 , але мають протилежний напрям. При цьому під силою ваги G розуміють вагу рідини в об’ємі АВСD, хоча останній не заповнений рідиною; тіло тиску V_ТТ є фіктивним.

Слід відмітити, що в тих випадках, коли циліндрична поверхня є коловою, лінія дії рівнодіючої сил тиску напрямлена по радіусу.

3 Основи кінематики і динаміки рідини

3.1 Основні поняття і визначення

Кінематика і динаміка рідини /гідродинаміка/ суттєво відрізняється від кінематики і динаміки твердого тіла. Якщо окремі частини абсолютно твердого тіла жорстко з’єднані між собою, то в рухомій рідині такі зв’язки відсутні: рідке середовище складається з безлічі частинок, які рухаються одна відносно другої. Тому в основу вивчення законів гідродинаміки покладена так звана струминкова модель, що базується на наступних поняттях.

Траєкторія – лінія, вздовж якої рухається деяка частинка рідини.

Рис.3.1

Лінія течії –це крива, що проходить через такі частинки, швидкості яких в даний час напрямлені по дотичним до цієї лінії (рис 3.1).

Рис.3.2

Трубкою течії називають трубчасту поверхню, яка утворена лініями течії, що проходять через всі точки нескінченно малого замкнутого контуру. (рис.3.2).

Частина рідини, що рухається всередині трубки течії, називається елементарною струминкою.

Властивості елементарної струминки при усталеному русі рідини.

1. Так як лінії течії при усталеному русі не змінюють своєї форми з часом, то, і струминка буде незмінною в часі.

2. Оскільки бокова поверхня струминки утворена лініями течії, то проникання рідини через цю поверхню неможливо.

3. Внаслідок малості площини поперечного перерізу елементарної струминки швидкість u і тиск р для всіх точок даного перерізу можна вважати однаковими.

Потоком рідини називають сукупність елементарних струминок.

Русло потоку – поверхня, яка обмежує потік по всій його довжині.

Потоки, що мають вільну поверхню, називають безнапірними потоки, які обмежені з усіх боків твердими стінками, називають напірними.

Живим перерізом (або перерізом) потоку називається в загальному випадку поверхня в межах потоку, перпендикулярна до всіх елементарних струминок.

Довжина лінії , по якій рідина в живому перерізі стикається з твердими стінками русла, називається змоченим периметром і позначається χ.

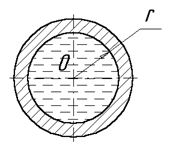
Відношення площі живого перерізу ω до довжини змоченого периметра називають гідравлічним радіусом R_Г (рис.3.3):

(3.1)

Витратою називають кількість рідини, що протікає через даний живий переріз за одиницю часу. Цю кількість вимірюють в одиницях об’єму – ; чи в одиницях маси – масова витрата . Зв’язок між ними дає співвідношення

(3.2)

Для елементарної струминки з рівномірним розподілом швидкостей u по живому перерізу об’ємна витрата

(3.3)

Рис.3.3

Об’ємна витрата потоку дорівнює сумі об’ємних витрат елементарних струминок, з яких складається потік,

(3.4)

В інженерних розрахунках користуються поняттям середньої швидкості по живому перерізу υ:

(3.5)

Під середньою швидкістю розуміється уявна, однакова для всіх точок живого перерізу потоку швидкість, при якій через цей переріз проходить таж витрата, що і при дійсних швидкостях в різних точках даного перерізу.

Тоді для потоку

(3.6)

3.2 Рівняння нерозривності для усталеного руху рідини

Умова руху рідини без утворення розривів (порожнин) характеризується рівнянням нерозривності (суцільності), яке виражає закон збереження маси.

Для елементарної струминки на основі її властивостей кількість рідини, що проходить в одиницю часу по всій довжині струминки, однакова. Тобто, для двох довільних перерізів 1і 2 струминки (рис 3.2).

,

або

(3.7)

Рівняння (3.7) називають рівнянням нерозривності для елементарної струминки.

Для потоку рідини при відсутності відводів чи припливів рівняння нерозривності є умовою сталості витрати:

,

чи

.

(3.8)

Останнє рівняння можна записати у вигляді

,

(3.9)

звідкіля виходить, що середні швидкості руху рідини в перерізах обернено пропорційні площам цих перерізів.

3.3 Рівняння Бернуллі при усталеному русі ідеальної рідини

Розглянемо усталений рух ідеальної рідини, яка знаходиться під впливом тільки масової сили – сили ваги, - і отримаємо для цього випадку рівняння, що зв’язує між собою тиск в рідині і швидкість її руху.

Рис.3.4

Візьмемо одну з елементарних струминок потоку ідеальної рідини і виділимо на ній ділянку довільної довжини, обмежену перерізами 1–1 і 2–2 (рис.3.4). Позначимо через dω₁ , p₁ , u₁ , z₁ і dω₂ , p₂ , u₂ , z₂ відповідно площі живих перерізів, гідродинамічні тиски, швидкості рідини і висоти центрів ваги даних перерізів над площиною порівняння 0–0.

За нескінченно малий проміжок часу dt відсік 1–2 переміститься в положення .

Застосуємо до виділеного відсіку теорему механіки про зміну кінетичної енергії, згідно з якою приріст кінетичної енергії відсіку за певний проміжок часу дорівнює сумі робіт всіх сил, що діють на відсік за цей же проміжок часу. Оскільки рідина ідеальна, то роботу будуть виконувати сили тиску і сили тяжіння.

Робота сил тиску буде дорівнювати:

.

Робота сил ваги:

.

Приріст кінетичної енергії відсіку 1–2 за час dt дорівнює різниці кінетичних енергій ділянок струминки (ділянка 1-2’ не змінює свого положення):

,

(при перетвореннях враховано, що ; )/

Тоді теорема про зміну кінетичної енергії відсіку струминки буде мати вигляд:

.

(3.10)

Поділимо попереднє рівняння на dQdt і після перегрупування складових його отримаємо

.

(3.11)

Якщо поділити рівняння (3.13) на комплекс , то після перегрупування складових будемо мати

.

(3.12)

Останні два рівняння і є рівнянням Бернуллі для елементарної струминки ідеальної рідини в двох різних формах. Так, всі складові в рівнянні (3.11) мають розмірність тиску, а складові рівняння (3.12) – лінійну розмірність.

З’ясуємо геометричну і фізичну суть рівняння Бернуллі/

Геометрична інтерпретація рівняння:

z – геометрична висота, або геометричний напір;

– п’єзометрична висота, або п’єзометричний напір;

– швидкісна висота, або швидкісний напір.

Тричлен називають повним, або гідродинамічним напором. Оскільки рівняння Бернуллі записане для довільних перерізів струминки, то H₀ =const в будь-якому перерізі цієї струминки (рис.3.5).

Рис.3.5

З енергетичної точки зору рівняння Бернуллі є законом збереження питомої енергії ідеальної рідини. Дійсно, якщо рівняння (3.11) записати у вигляді

,

то – питома енергія положення, Дж/кг;

– питома енергія тиску, Дж/кг;

– питома потенціальна енергія рідини, Дж/кг;

– кінетична енергія віднесена до одиниці маси, Дж/кг.

Можна теоретично довести, що для потоку ідеальної рідини з повільно-змінним рухом сума z+p/ρg для всіх точок живого перерізу є постійною. Крім того, в даному живому перерізі потоку ідеальної рідини швидкості всіх елементарних струминок однакові. Тому рівняння Бернуллі для потоку ідеальної рідини має такий же вигляд як і для елементарної струминки, тобто дається формулами (3.11) і (3.12).

3.4 Рівняння Бернуллі для елементарної струминки і потоку в’язкої рідини

На відміну від ідеальної рідини при русі в’язкої(реальної) рідини частина енергії, яку вона має, витрачається на подолання сил опору (внутр. тертя, вихроутвор. та ін.). Отже питома енергія в будь-якому наступному в напрямі течії поперечному перерізі буде меншою порівняно з питомою енергією в попередньому перерізі. Тому рівняння Бернуллі для елементарної струминки реальної рідини буде мати вигляд

.

(3.13)

де – втрати енергії (напору) струминки між обраними перерізами.

Рівняння Бернуллі для потоку реальної рідини отримують інтегруванням рівняння (3.13) з заміною дійсних швидкостей окремих струминок, що утворюють потік, на середню швидкість υ рідини в даному перерізі (рис.3.6):

.

(3.14)

Коефіцієнт α, що входить до рівняння Бернуллі, називають коефіцієнтом кінематичної енергії або коефіцієнтом Коріоліса. Він враховує нерівномірність розподілу швидкостей в перерізі потоку і фактично є відношенням дійсної кінетичної енергії потоку в даному живому перерізі до кінетичної енергії, обчисленої за середньою швидкістю потоку. Величина коефіцієнта α в залежності від характеру течії рідини змінюється в межах від 1,04…1,12 до 2. Складова рівняння – це сумарні втрати питомої енергії (напору) потоку між обраними перерізами.

Запишемо рівняння Бернуллі (3.14) в такій формі:

,

(3.14’)

де і – повні гідродинамічні напори потоку в перерізах 1–1 та 2–2 відповідно.

Відношення втрат напору до довжини ділянки потоку, обмеженої перерізами 1–1 і 2–2, називають гідравлічним уклоном, або градієнтом втрат напору:

,

(3.15)

тут l – довжина ділянки, м.

3.5 Гідравлічні опори і втрати енергії (напору) при русі рідини

Втрати питомої енергії при русі в’язкої рідини, або, як часто їх називають, гідравлічні втрати, обумовлені різними гідравлічними опорами, механізми яких настільки складні, що не дають змоги отримати теоретичні залежності для розрахунків втрат напору. Експериментально доведено, що гідравлічні втрати в значній мірі залежать від швидкості руху рідини, тому в гідравліці їх виражають в частках швидкісного напору за формулою:

(3.16)

в якій ξ - безрозмірний коефіцієнт пропорційності (коефіцієнт гідравлічних опорів); він показує частку швидкісного напору, яку складає втрачений напір.

Розрізняють два види гідравлічних опорів: місцеві і лінійні опори. Місцеві опори проявляються на коротких ділянках потоку при зміні напряму течії рідини, зміні форми чи величини поперечного перерізу потоку. Напір, що втрачається на долання місцевих опорів, визначають за формулою Вейсбаха:

(3.17)

де ξ_М – коефіцієнт місцевого опору, який залежить від виду опору і наводиться в довідниках.

Лінійні опори обумовлені силами внутрішнього тертя і виникають по всій довжині потоку рідини, тому вони пропорційні довжині потоку. Втрати напору по довжині (лінійні втрати) визначають за формулою:

,

(3.18)

де λ – коефіцієнт гідравлічного тертя (коефіцієнт Дарсі); l – довжина ділянки потоку, на якій підраховують втрати енергії; R_Г – гідравлічний радіус живого перерізу потоку.

Для круглих циліндричних труб діаметр труби d = 4R_Г , отже лінійні втрати:

.

(3.19)

Сумарні втрати енергії (напору) між двома живими перерізами потоку, що входять до рівняння Бернуллі будуть дорівнювати:

,

(3.20)

де - сума втрат напору по довжині на всіх ділянках русла в межах обраних перерізів; – сума всіх місцевих втрат.

3.6 Режими руху рідини. Критерій Рейнольдса

Експериментальні дослідження показали, що втрати енергії при русі в’язкої рідини суттєво залежать від режиму руху рідини. На наявність різних за структурою потоків режимів течії звернули увагу ще в першій половині ХІХ сторіччя (Хаген, Дарсі та ін.). В 1880 р. Д.І.Менделеєв вказав на наявність двох різних видів руху рідини, які відрізняються один від одного характером залежності сил тертя від швидкості руху. А в 1883 р. англійський фізик Осборн Рейнольдс обґрунтував теоретично і наочно показав існування двох принципово різних режимів течії рідини : ламінарного (від латинського lamina –шар) і турбулентного (від лат. turbulentus - безладний ).

Ламінарний режим характеризується шаруватою течією рідини без перемішування окремих її шарів і без пульсацій швидкості і тиску. Ламінарний режим може установлюватися в капілярних трубках при малих швидкостях руху води, а також при русі рідин з великою в’язкістю (нафта, масла, гліцерин тощо).

При турбулентному режимі течія рідини супроводжується інтенсивним перемішуванням окремих її частинок і пульсаціями швидкостей і тиску. Цей режим характерний при русі води в системах водопостачання і інших рідин при відносно великих швидкостях руху.

Рейнольдс встановив, що критерієм режиму руху рідини є безрозмірна величина, яка являє собою відношення добутку швидкості потоку на характерний лінійний розмір до коефіцієнта кінематичної


29-04-2015, 00:58