Примеры t -конорм:
max(mA , mB )
mA + mB - mA ×mB
min(1, mA + mB ).
Алгебраические операции над нечеткими множествами
Алгебраическое произведение A и B обозначается A ×B и определяется так:
"x ÎE mA ×B (x ) = mA (x ) mB (x ).
Алгебраическая сумма
этих множеств обозначается ![]() и определяется так:
и определяется так:
"
x
Î
E
![]() =
m
A
(x
) +
m
B
(x
)
-m
A
(x
)
m
B
(x
).
=
m
A
(x
) +
m
B
(x
)
-m
A
(x
)
m
B
(x
).
Для операций {×, ![]() } выполняются свойства:
} выполняются свойства:
![]() - коммутативность;
- коммутативность;
![]() - ассоциативность;
- ассоциативность;
A×Æ = Æ, A![]() Æ = A, A×E = A, A
Æ = A, A×E = A, A![]() E = E
E = E
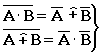 - теоремы де Моргана.
- теоремы де Моргана.
Не выполняются:
![]() - идемпотентность;
- идемпотентность;
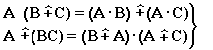 - дистрибутивность;
- дистрибутивность;
а также A×![]() = Æ, A
= Æ, A![]()
![]() = E.
= E.
Замечание . Доказательства приводимых свойств операций над нечеткими множествами мы оставляем читателю.
Для примера докажем свойство: ![]() . Обозначим mA
(x
)
через a
, mB
(x
)
через b
. Тогда в левой части для каждого элемента х
имеем: 1-ab
, а в правой: (1-a
)+(1-b
)-(1-a
)(1-b
) = 1-a
+1-b
-
1+a
+b-ab
= 1-ab
.
. Обозначим mA
(x
)
через a
, mB
(x
)
через b
. Тогда в левой части для каждого элемента х
имеем: 1-ab
, а в правой: (1-a
)+(1-b
)-(1-a
)(1-b
) = 1-a
+1-b
-
1+a
+b-ab
= 1-ab
.
Докажем, что свойство дистрибутивности не выполняется, т.е. A
×(B![]() C)
¹ (A
×B)
C)
¹ (A
×B)![]() (A
×C)
. Для левой части имеем: a
(b
+c-bc
) = ab
+ac-abc
; для правой: ab
+ac
-(ab
)(ac
) = ab
+ac
+a
2
bc
. Это означает, что дистрибутивность не выполняется при a
¹a
2
.
(A
×C)
. Для левой части имеем: a
(b
+c-bc
) = ab
+ac-abc
; для правой: ab
+ac
-(ab
)(ac
) = ab
+ac
+a
2
bc
. Это означает, что дистрибутивность не выполняется при a
¹a
2
.
Замечание. При совместном использовании операций {È, Ç,+,×} выполняются свойства:
А×(BÈC) = (A×B)È(A × C);
А× (BÇC) = (A×B)Ç(A×C);
А![]() (BÈC) = (A
(BÈC) = (A![]() B)È(A
B)È(A![]() C);
C);
А![]() (BÇC)=(A
(BÇC)=(A![]() B)Ç(A
B)Ç(A![]() C).
C).
Продолжим обзор основных операций над нечеткими множествами.
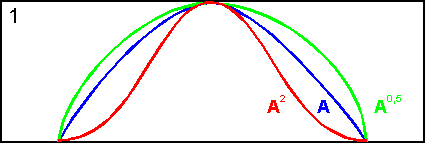
На основе операции алгебраического произведения (по крайней мере для целых a эта основа очевидна) определяется операция возведения в степень a нечеткого множества A , где a - положительное число. Нечеткое множество A a определяется функцией принадлежности mA a = ma A (x) . Частным случаем возведения в степень являются:
CON(A) = A2 - операция концентрирования ,
DIL(A) = A0,5 - операция растяжения ,
которые используются при работе с лингвистическими неопределенностями.
Умножение на число.
Если a
- положительное число, такое, что a![]() mA
(x
)
£
1, то нечеткое множество aA
имеет функцию принадлежности:
mA
(x
)
£
1, то нечеткое множество aA
имеет функцию принадлежности:
maA(x ) = amA(x ).
Выпуклая комбинация нечетких множеств. Пусть A 1 , A 2 ,.., A n - нечеткие множества универсального множества E , а w1 , w2 , ..., wn - неотрицательные числа, сумма которых равна 1.
Выпуклой комбинацией A 1 , A 2 ,.., A n называется нечеткое множество A с функцией принадлежности:
"x ÎE mA (x 1 , x 1 ,..., x n ) = w1 mA1 (x ) + w2 mA2 (x ) + ... + w n m Ai (x ).
Декартово произведение нечетких множеств. Пусть A 1 , A 2 , ..., A n - нечеткие подмножества универсальных множеств E 1 , E 2 , ..., E n соответственно. Декартово произведение A = A 1 ´A 2 ´ ...´A n является нечетким подмножеством множества E = E 1 ´E 2 ´... ´E n с функцией принадлежности:
mA (x 1 , x 1 , ..., x n ) = min{ mA1 (x 1 ), mA2 (x 2 ) , ... , mAi (x n ) }.
Оператор увеличения нечеткости используется для преобразования четких множеств в нечеткие и для увеличения нечеткости нечеткого множества.
Пусть A - нечеткое множество, E - универсальное множество и для всех x ÎE определены нечеткие множества K(х ) . Совокупность всех K(х ) называется ядром оператора увеличения нечеткости Ф . Результатом действия оператора Ф на нечеткое множество A является нечеткое множество вида:
Ф(A, K) = ![]() mA
(x
)K(х
),
mA
(x
)K(х
),
где mA (x )K(х ) - произведение числа на нечеткое множество.
Пример :
E = {1,2,3,4};
A = 0,8/1+0,6/2+0/3+0/4;
K (1) = 1/1+0,4/2;
K (2) = 1/2+0,4/1+0,4/3;
K (3) = 1/3+0,5/4;
K (4) = 1/4.
Тогда
Ф (A,K) = mA (1) K (1) Èm A (2)K (2) Èm A (3)K (3)Èm A (4)K (4) =
= 0,8(1/1+0,4/2) È 0,6(1/2+0,4/1+0,4/3) =
= 0,8/1+0,6/2+0,24/3.
Четкое множество a-уровня (или уровня a) . Множеством a-уровня нечеткого множества A универсального множества E называется четкое подмножество A a универсального множества E , определяемое в виде:
A a ={x /mA (x )³a}, где a£1.
Пример: A = 0,2/x1 + 0/x2 + 0,5/x3 + 1/x4 ,
тогда A0.3 = {x 3 ,x 4 },
A0.7 = {x 4 }.
Достаточно очевидное свойство: если a1 ³a2 , то A a1 £A a2 .
Теорема о декомпозиции. Всякое нечеткое множество A разложимо по его множествам уровня в виде:
A
= ![]() aA
a
, где aA
a
- произведение числа a
на множество A
, и a
"пробегает" область значений M
функции принадлежности нечеткого множества A
.
aA
a
, где aA
a
- произведение числа a
на множество A
, и a
"пробегает" область значений M
функции принадлежности нечеткого множества A
.
Пример: A = 0,1/x 1 + 0/x 2 + 0,7/x 3 + 1/x 4 представимо в виде:
A = 0,1(1,0,1,1) È 0,7(0,0,1,1,) È 1(0,0,0,1)=
= (0,1/x1 + 0/x2 + 0,1/x3 + 0,1/x4 )È (0/x1 + 0/x2 + 0,7/x3 + 0,7/x4 )È
È(0/x1 + 0/x2 + 0/x3 + 1/x4 ) = 0,1/x1 +0/x2 +0,7/x3 +1/x4 .
Если область значений функции принадлежности состоит из n градаций a1 £a2 £a3 £ ...£an , то A (при фиксированных значениях градаций) представимо в виде:
A
= ![]() a
i
A
a
i
,
a
i
A
a
i
,
т.е. определяется совокупностью обычных множеств { A a1 , A a2 , ..., A ai }, где A a1 ³A a2 ³ , ..., ³A ai .
Расстояние между нечеткими множествами, индексы нечеткости
Пусть A и B - нечеткие подмножества универсального множества E . Введем понятие расстояния r(A , B ) между нечеткими множествами. При введении расстояния обычно предъявляются следующие требования:
r(A, B ) ³ 0 - неотрицательность;
r(A, B ) = r(B, A ) - симметричность;
r(A, B ) < r(A, C ) + r(C, B ).
К этим трем требованиям можно добавить четвертое: r(A, A ) = 0.
Определим следующие расстояния по формулам:
Расстояние Хемминга (или линейное расстояние ):
r(A, B
) = ![]() ½m
A
(xi
) - m
B
(xi
)½ .
½m
A
(xi
) - m
B
(xi
)½ .
Очевидно, что r(A, B )Î[0, n ].
Евклидово или квадратичное расстояние:
e(A, B
) = 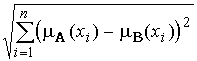 , e(A, B
)Î[0,
, e(A, B
)Î[0, ![]() ].
].
Относительное расстояние Хемминга:
r(A, B
) = ![]()
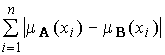 , r(A, B
)Î[0,1].
, r(A, B
)Î[0,1].
Относительное евклидово расстояние:
e(A, B
)=![]()
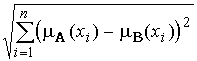 , e(A, B
)Î[0,1].
, e(A, B
)Î[0,1].
Расстояние Хемминга и квадратичное расстояние, в случае когда E бесконечно, определяются аналогично с условием сходимости соответствующих сумм:
если E счетное, то
r(A, B
) = ![]() ½m
A
(xi
) - m
B
(xi
)½ ,
½m
A
(xi
) - m
B
(xi
)½ ,
e(A,
B
) = 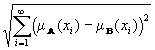 ;
;
если E = R (числовая ось), то
r(A, B
) = 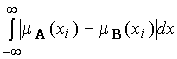 ,
,
e(A, B
) = 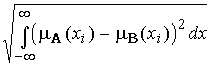 .
.
Замечание. Здесь приведены два наиболее часто встречающихся определения понятия расстояния. Разумеется, для нечетких множеств можно ввести и другие определения понятия расстояния.
Перейдем к индексам нечеткости или показателям размытости нечетких множеств.
Если объект х обладает свойством R (порождающим нечеткое множество A ) лишь в частной мере, т.е.
0<
mA
(x
)
<1, то внутренняя неопределенность, двусмысленность объекта х
в отношении R
проявляется в том, что он, хотя и в разной степени, принадлежит сразу двум противоположным классам: классу объектов, "обладающих свойством R
", и классу объектов, "не обладающих свойством R
". Эта двусмысленность максимальна, когда степени принадлежности объекта обеим классам равны, т.е. mA
(x
) = ![]() (x
) = 0,5, и минимальна, когда объект принадлежит только одному классу, т.е. либо mA
(x
) = 1 и
(x
) = 0,5, и минимальна, когда объект принадлежит только одному классу, т.е. либо mA
(x
) = 1 и ![]() (x
)
= 0, либо mA
(x
) = 0 и
(x
)
= 0, либо mA
(x
) = 0 и ![]() (x
)
= 1.
(x
)
= 1.
В общем случае показатель размытости нечеткого множества можно определить в виде функционала d(A) со значениями в R (положительная полуось), удовлетворяющего условиям:
d(A) = 0 тогда и только тогда, когда А - обычное множество;
d(A) максимально тогда и только тогда, когда mA (x ) = 0.5 для всех x ÎE .
d(A)d(B) , если A является заострением B , т.е.
mA (x )£mB (x ) при mB (x ) < 0,5;
mA (x )³mB (x ) при mB (x ) > 0,5;
mA (x )- любое при mB (x ) = 0,5.
d(A) = d
(![]() ) - симметричность по отношению к 0,5.
) - симметричность по отношению к 0,5.
d(AÈB)+d(AÇB) = d(A)+d(B).
Замечание. Приведенная система аксиом при введении конкретных показателей размытости часто используется частично, т.е., например, ограничиваются свойствами P1, P2 и P3 , либо некоторые свойства усиливаются или ослабляются в зависимости от решаемой задачи.
Рассмотрим индексы нечеткости (показатели размытости), которые можно определить, используя понятие расстояния.
Обычное множество, ближайшее к нечеткому
Пусть A - нечеткое множество. Вопрос: какое обычное множество A ÌE является ближайшим к A , т.е. находится на наименьшем евклидовом расстоянии от нечеткого множества A . Таким подмножеством, обозначаемым A , является подмножеством с характеристической функцией:
 .
.
Обычно принимают mA (xi ) = 0, если mA (xi ) = 0,5.
Используя понятие обычного множества, ближайшего к нечеткому, введем следующие индексы нечеткости нечеткого множества А .
Линейный индекс нечеткости:
![]()
Здесь r(A, A
) - линейное (хеммингово) расстояние, множитель - ![]() обеспечивает выполнение условия 0<
d(A
)<
1.
обеспечивает выполнение условия 0<
d(A
)<
1.
Квадратичный индекс нечеткости
![]() , 0<
d(A
)<
1.
, 0<
d(A
)<
1.
Здесь e(A, A ) - квадратичное (евклидово) расстояние.
Замечания.
1. Мы ввели линейный и квадратичный индексы нечеткости, используя понятие расстояния и понятие обычного множества, ближайшего к нечеткому. Эти же индексы можно определить, используя операцию дополнения, следующим образом:
![]() - линейный индекс,
- линейный индекс,
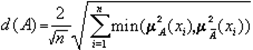 - квадратичный индекс.
- квадратичный индекс.
2. Отметим следующие свойства, связанные с ближайшим обычным множеством:
А ÇВ =А ÇВ ,
А ÈВ =А ÈВ ;
а также "x
ÎE:|
mA
(xi
)-
mA
(xi
)|=
![]() , откуда для линейного индекса нечеткости имеем:
, откуда для линейного индекса нечеткости имеем:
![]() ,
,
т.е. в этом представлении становится очевидным, что d(A
)=d(![]() ).
).
3. Нечеткое множество с функцией принадлежности ![]() иногда называют векторным индикатором нечеткости.
иногда называют векторным индикатором нечеткости.
Оценка нечеткости через энтропию
Ограничимся случаем конечного универсального множества. Энтропия системы с n состояниями e1 ,e2 , ..., en , с которыми связаны вероятности p1 ,p2 , ..., pn определяется выражением:
H(p
1
, p
2
, ..., p
n
) = - ![]() p
i
ln p
i
, Hmin
= 0, Hmax
= 1.
p
i
ln p
i
, Hmin
= 0, Hmax
= 1.
В случае нечетких множеств положим:
pA
(xi
) = 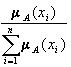
Тогда общую формулу, позволяющую подсчитать энтропию по нечеткости, можно записать в следующем виде:
H(pA
(x1
), pA
(x2
), ..., pA
(xn
)) = - ![]() pA
(xi
) ln pA
(xi
).
pA
(xi
) ln pA
(xi
).
Замечание. Попытки использования энтропии в теории нечетких множеств (в приведенном выше виде) показали, что это не лучший способ оценки. Однако работы по обобщению понятия энтропии для нечетких множеств продолжаются.
Принцип обобщения
Принцип обобщения - одна из основных идей теории нечетких множеств - носит эвристический характер и используется для расширения области применения нечетких множеств на отображения. Пусть X и Y - два заданных универсальных множества. Говорят, что имеется функция, определенная на X со значением в Y , если, в силу некоторого закона f, каждому элементу X ÎX соответствует элемент yÎY .
Когда функцию f: X ®Y называют отображением, значение f(x)ÎY , которое она принимает на элементе xÎX , обычно называют образом элемента x.
Образом множества А ÌХ при отображении с®Y называют множество f(A )ÌY тех элементов Y , которые являются образами элементов множества А .
Замечание. Мы напомнили классическое определение отображения, которое в теории нечетких множеств принято называть четким отображением, т.к. наряду с ним мы введем понятие нечеткого отображения (или нечеткой функции).
Будем говорить, что имеется нечеткая функция f, определенная на X
со значением в Y
, если она каждому элементу xÎX
ставит в соответствие элемент yÎY
со степенью принадлежности mf
(x,y). Нечеткая функция f определяет нечеткое отображение f:X
![]() Y
.
Y
.
Принцип обобщения заключается в том, что при заданном четком f:X
®Y
или нечетком f:X
![]() Y
отображении для любого нечеткого множества А
, заданного на Х
, определяется нечеткое множество f(A
) на Y
, являющееся образом A
.
Y
отображении для любого нечеткого множества А
, заданного на Х
, определяется нечеткое множество f(A
) на Y
, являющееся образом A
.
Пусть f:X ®Y заданное четкое отображение,
а A = {mA (x)/х}- нечеткое множество в Х . Тогда образом А при отображении f является нечеткое множество f(A ) на Y с функцией принадлежности:
m
f(A)
(y) = ![]() m
A
(x); yÎY
,
m
A
(x); yÎY
,
где f -1 (y)={x/f(x)=y}.
В случае нечеткого отображения f:X
![]() Y
, когда для любых xÎX
и yÎY
определена двуместная функция принадлежности mf
(x,y), образом нечеткого множества А
, заданного на Х, является нечеткое множество f(A
) на Y
с функцией принадлежности:
Y
, когда для любых xÎX
и yÎY
определена двуместная функция принадлежности mf
(x,y), образом нечеткого множества А
, заданного на Х, является нечеткое множество f(A
) на Y
с функцией принадлежности:
m
f(A)
(y) = ![]() min(
m
A
(x), m
f
(x,y)).
min(
m
A
(x), m
f
(x,y)).
Замечание. Мы не приводим примеров использования принципа обобщения. Предлагаем подумать, каким образом можно определить нечеткое число и как с помощью принципа обобщения (не забывая декартова произведения) и классических операций возведения числа в степень(одноместная), сложения и умножения (двуместные) получать соответствующие нечеткие результаты. К нечетким отображениям мы вернемся, когда будем рассматривать понятие нечеткого отношения.
2. НЕЧЕТКИЕ ОТНОШЕНИЯ
Пусть Е = Е1 ´Е2 ´ ... ´Еn - прямое произведение универсальных множеств и М - некоторое множество принадлежностей (например М = [0,1]). Нечеткое n-арное отношение определяется как нечеткое подмножество R на E , принимающее свои значения в М . В случае n =2 и М = [0,1], нечетким отношением R между множествами X = Е1 и Y = Е2 будет называться функция R:(X,Y) ® [0,1], которая ставит в соответствие каждой паре элементов (х,y)ÎX ´Y величину mR (x,y) Î[0,1]. Обозначение: нечеткое отношение на X ´Y запишется в виде: xÎX , yÎY : xRy . В случае, когда X = Y , т.е. X и Y совпадают, нечеткое отношение R: X´X®[0,1] называется нечетким отношением на множестве X .
Примеры:
Пусть X = {x1 ,x2 ,x3 }, Y = {y1 ,y2 ,y3 ,y4 }, М = [0,1]. Нечеткое отношение R=XRY может быть задано, к примеру, таблицей:
| y1 | y2 | y3 | y4 | |
| x1 | 0 | 0 | 0,1 | 0,3 |
| x2 | 0 | 0,8 | 1 | 0,7 |
| x3 | 1 | 0,5 | 0,6 | 1 |
Пусть X
= Y
= (-![]() ,
, ![]() ), т.е. множество всех действительных чисел. Отношение x>>y (x много больше y) можно задаеть функцией принадлежности:
), т.е. множество всех действительных чисел. Отношение x>>y (x много больше y) можно задаеть функцией принадлежности: 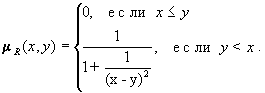
Отношение R , для которого mR (x,y) = e -k(x-y)2 , при достаточно больших k можно интерпретировать так: "x и y близкие друг к другу числа".
В случае конечных или счетных универсальных множеств очевидна интерпретация нечеткого отношения в виде нечеткого графа, в котором пара вершин (xi ,xj ) в случае XRX соединяется ребром с весом mR (xi ,xj ), в случае XRY пара вершин (xi ,yj ) соединяется ребром c весом mR (xi ,yj ).
Примеры:
Пусть Х={x1 ,x2 ,x3 }, и задано нечеткое отношение R: X´X® [0,1], представимое графом:
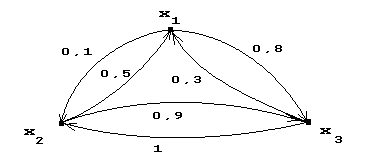
Пусть X={x1 ,x2 } и Y={y1 ,y2 ,y3 }, тогда нечеткий граф вида:
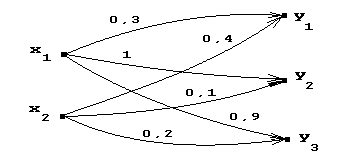
задает нечеткое отношение XRY .
Замечание.
В общем случае нечеткий граф может быть определен на некотором G
ÌX
´Y
, где G
- множество упорядоченных пар (x,y) (необязательно всех возможных) такое, что G
Ç![]() = Æ и G
È
= Æ и G
È![]() = X
´Y
.
= X
´Y
.
Будем использовать обозначения ![]() вместо
вместо ![]() и
и ![]() вместо
вместо ![]() .
.
Пусть R : X ´Y ®[0,1].
Носитель нечеткого отношения.
Носителем нечеткого отношения R называется обычное множество упорядоченных пар (x,y), для которых функция принадлежности положительна:
S(R) ={(x,y): m R (x,y)>0}.
Нечеткое отношение содержащее данное нечеткое отношение, или содержащееся в нем.
Пусть R1 и R2 - два нечетких отношения такие, что:
"(x,y)ÎX ´Y : mR1 (x,y)£m R2 (x,y),
тогда говорят, что R2 содержит R1 или R1 содержится в R2 .
Обозначение: R1 ÍR2 .
Пример:
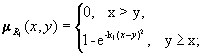
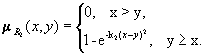
Отношения R1 , R2 - отношения типа y>>x (y много больше x). При k2 > k1 отношение R2 содержит R1 .
Операции над нечеткими отношениями
Объединение двух отношений R1 и R2 .
Объединение двух отношений обозначается R1 ÈR2 и определяется выражением:
mR1 ÈR2 (x,y) = mR1 (x,y)Ú mR2 (x,y)
Примеры:
1. Ниже изображены отношения действительных чисел, содержательно означающие: xR1 y - "числа x и y очень близкие", xR2 y - "числа x и y очень различны" и их объединение xR1 ÈR2 y - "числа x и y очень близкие или очень различные".
Функции принадлежности отношений заданы на |y-x|. 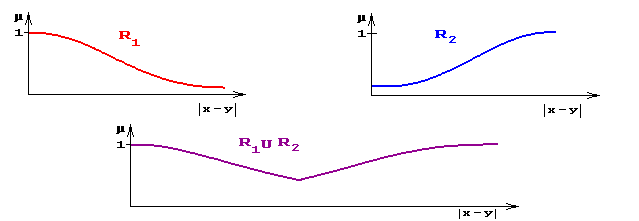
| mR1 È R2 (x,y) = | |
mR1 (x,y), | y - x | £a mR2 (x,y), | y - x | >a |
где a - такое |y-x|, что m R1 (x,y) = m R2 (x,y)
2.
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Пересечение двух отношений.
Пересечение двух отношений R1 и R2 обозначается R1 ÇR2 и определяется выражением:
mR1 ÇR2 (x,y) = mR1 (x,y)Ù mR2 (x,y)
.
Примеры:
1. Ниже изображены отношения: xR1 y, означающее "модуль разности |y-x| близок к a", xR2 y, означающее "модуль разности |y-x| близок к b", и их пересечение.
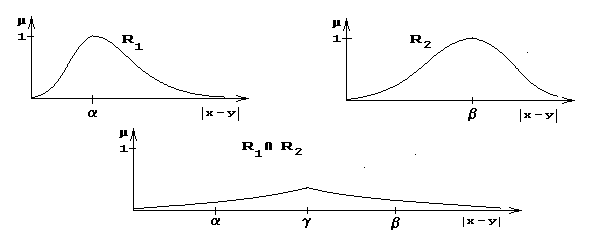
Алгебраическое произведение двух отношений.
Алгебраическое произведение двух отношений R1 и R2 обозначается R1 ×R2 и определяется выражением:
mR1 ×R2 (x,y) = mR1 (x,y)×mR2 (x,y)
Алгебраическая сумма двух отношений.
Алгебраическая сумма двух отношений R1
и R2
обозначается R1
![]() R2
и определяется выражением:
R2
и определяется выражением: ![]() .
.
Для введенных операций справедливы следующие свойства дистрибутивности:
R1 Ç(R2 ÈR3 ) = (R1 ÇR2 )È(R1 ÇR3 ),
R1 È(R2 ÇR3 ) = (R1 ÈR2 )Ç(R1 ÈR3 ),
R1 ×(R2 ÈR3 ) = (R1 ×R2 )È(R1 ×R3 ),
R1 ×(R2 ÇR3 ) = (R1 ×R2 )Ç(R1 × R3 ),
R1
![]() (R2
ÈR3
) = (R1
(R2
ÈR3
) = (R1
![]() R2
)È(R1
R2
)È(R1
![]() R3
),
R3
),
R1
![]() (R2
ÇR3
) = (R1
(R2
ÇR3
) = (R1
![]() R2
)Ç (R1
R2
)Ç (R1
![]() R3
).
R3
).
Дополнение отношения.
Дополнение отношения R
29-04-2015, 02:39
