![]() (x,y) = 1 - m
R
(x,y)
(x,y) = 1 - m
R
(x,y)
.
Дизъюнктивная сумма двух отношений.
Дизъюнктивная сумма двух отношений R1 и R2 обозначается RÅR и определяется выражением:
R1
ÅR2
= (R1
Ç![]() 2
)È(
2
)È(![]() 1
ÇR2
) .
1
ÇR2
) .
Обычное отношение, ближайшее к нечеткому.
Пусть R - нечеткое отношение с функцией принадлежности mR (x,y). Обычное отношение, ближайшее к нечеткому, обозначается R и определяется выражением:
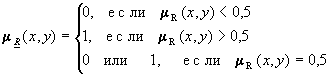
По договоренности принимают mR (x,y)=0 при mR (x,y) = 0,5.
Проекции нечеткого отношения.
Пусть R
- нечеткое отношение R
: (x,y)®[0,1]. Первой проекцией ![]() отношения R
(проекция на X
) называется нечеткое множество
отношения R
(проекция на X
) называется нечеткое множество ![]() , заданное на множестве X
, с функцией принадлежности:
, заданное на множестве X
, с функцией принадлежности:
![]() .
.
Аналогично, второй проекцией ![]() (проекцией на Y
) называется нечеткое множество
(проекцией на Y
) называется нечеткое множество ![]() , заданное на множестве Y
, с функцией принадлежности:
, заданное на множестве Y
, с функцией принадлежности:
![]() .
.
Величина h(R) = ![]() называется глобальной проекцией отношения R
. Если h(R)=1, то отношение R
нормально, в противном случае - субнормально.
называется глобальной проекцией отношения R
. Если h(R)=1, то отношение R
нормально, в противном случае - субнормально.
Пример:
| R = |
|
1-я проекция
|
= R 1' | ||||||||||||||||||||||||||
| R 2 ' = |
|
|
= h(R) | ||||||||||||||||||||||||||
| 2-я проекция | |||||||||||||||||||||||||||||
Цилиндрические продолжения проекций нечеткого отношения
Проекции R1
¢
и R2
¢
нечеткого отношения XRY
в свою очередь определяют в X
´Y
нечеткие отношения ![]() и
и ![]() с функциями принадлежности:
с функциями принадлежности:
![]() (x,y
)=
(x,y
)=![]() (x
) при любом y
,
(x
) при любом y
, ![]() (x,y
)=
(x,y
)=![]() (y
) при любом x
,
(y
) при любом x
,
называемые, соответственно, цилиндрическим продолжением R1 ' и цилиндрическим продолжением R2 '.
Замечание. Очевидно, что для любых нечетких подмножеств А и В , определенных, соответственно, на X и Y , можно построить их цилиндрические продолжения А и В .
Пример (продолжение):
Имеем:
| R1 ' = |
|
|
и
| R2 ' = |
|
|
|
Сепарабельность отношений
Нечеткое отношение XRY
называется сепарабeльным, если оно равно пересечению цилиндрических продолжений своих проекций, т.е. если R
= ![]() Ç
Ç
![]() , т.е. mR
(x,y
) =
, т.е. mR
(x,y
) = ![]() (x
)Ç
(x
)Ç
![]() (y
).
(y
).
Замечание. Если определено декартово произведение нечетких множеств (выше оно введено), то, очевидно, нечеткое отношение XRY сепарабельно, если оно является декартовым произведением своих проекций, т.е. R = R1 ' ´R2 ' .
Пример (продолжение):
|
¹R , |
т.е. исходное отношение R несепарабельно.
Композиция двух нечетких отношений
Композиция двух нечетких отношений
Пусть R1 - нечеткое отношение R1 : (X ´ Y )®[0,1] между X и Y, и R2 - нечеткое отношение R2 : (Y ´Z )® [0,1] между Y и Z. Нечеткое отношение между X и Z, обозначаемое R2 ·R1 , определенное через R1 и R2 выражением
mR1
·R2
(x,z
) = ![]() [mR1
(x,y
)Lm
R1
(y,z
)],
[mR1
(x,y
)Lm
R1
(y,z
)],
называется (max-min)-композицией отношений R1 и R2 .
Примеры:
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
m R1 · R2 (x 1 , z 1 ) = [mR1 (x 1 , y 1 ) Lm R2 (y 1 , z 1 )] V [m R1 (x 1 , y 2 ) Lm R2 (y 2 , z 1 )] V [m R1 (x 1 , y 3 ) Lm R2 (y 3 , z 1 )] =
= (0,1L0,9)V(0,7L0,3)V(0,4L0,1) = 0,1V0,3V0,1 = 0,3
m R1 · R2 (x 1 ,z 2 ) = (0,1L0)V(0,7L0,6)V(0,4L 1) = 0V0,6V0,4 = 0,6
m R1 · R2 (x 1 ,z 3 ) = 0,1
...................
...................
m R1 · R2 (x 2 ,z 5 ) = 0,5
Замечание . В данном примере вначале использован "аналитический" способ композиции отношений R1 и R2 , т.е. i -я строка R1 "умножается" на j -й столбец R2 с использованием операции L, полученный результат "свертывается" с использованием операции V в m (xi ,zj ).
Ниже приведены графы, соответствующие R1 и R2 , "склеенные" по Y. В полученном графе рассматриваем пути от xi к zj и каждому ставим в соответствие минимальный из "весов" его составляющих. Затем определяем максимум по всем путям из xi в zj , который и дает искомое m(xi ,zj ).
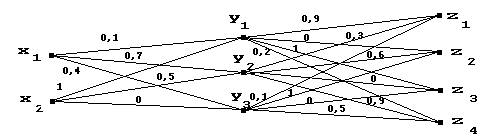
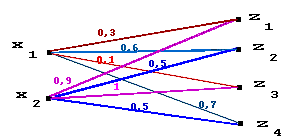
Свойства max-min композиции
Операция (max-min)-композиции ассоциативна, т.е.
R3 ·(R2 ·R1 ) = (R3 ·R2 )·R1 ,
дистрибутивна относительно объединения, но недистрибутивна относительно пересечения:
R3 ·(R2 È R1 ) = (R3 ·R2 )È (R3 ·R1 ),
R3 ·(R2 Ç R1 )¹(R3 · R2 )Ç(R3 · R1 ).
Кроме того, для (max-min)-композиции выполняется следующее важное свойство: если R1 ÌR2 то, R·R1 ÌR·R2 .
(max- *) - композиция
В выражении mR1
·R2
(x, z
) = ![]() [mR1
(x, y
)Lm
R2
(y, z
)] для (max-min)-композиции отношений R1
и R2
операцию L можно заменить любой другой, для которой выполняются те же ограничения, что и для L: ассоциативность и монотонность (в смысле неубывания) по каждому аргументу. Тогда:
[mR1
(x, y
)Lm
R2
(y, z
)] для (max-min)-композиции отношений R1
и R2
операцию L можно заменить любой другой, для которой выполняются те же ограничения, что и для L: ассоциативность и монотонность (в смысле неубывания) по каждому аргументу. Тогда:
mR1
·R2
(x, z
) = ![]() [mR1
(x, y
)*m
R1
(y, z
)]
[mR1
(x, y
)*m
R1
(y, z
)]
В частности, операция L может быть заменена алгебраическим умножением, тогда говорят о (max - prod)-композиции.
Обычное подмножество a - уровня нечеткого отношения
Обычным подмножеством a - уровня нечеткого отношения R называется четкое (обычное) отношение Ra такое, что
m
R1
(x,y
) = ![]()
Очевидно, что из a1 £a2 следует Ra1 ³ Ra2 .
Теорема декомпозиции
Любое нечеткое отношение R представимо в форме:
R = ![]() a×
Ra, 0<a£1,
a×
Ra, 0<a£1,
где a× Ra означает, что все элементы Ra умножаются на a.
Условные нечеткие подмножества.
Пусть X и Y - универсальные множества, взаимосвязь которых задана нечетким отношением R : (X ´Y )®[0,1], т.е. для каждой пары (x,y )ÎX ´Y задано значение функции принадлежности mR (x,y )Î[0,1].
Пусть А - некоторое нечеткое множество, заданное на Х , т.е. определена функция принадлежности mA (x ) для всех х из Х . Тогда нечеткое множество А и нечеткое отношение R индуцируют в Y нечеткое подмножество B с функцией принадлежности
m
B
(y
) = ![]() min[m
A
(x
), m
R
(x,y
)] =
min[m
A
(x
), m
R
(x,y
)] = ![]() [m
A
(x
)Lm
R
(x,y
)].
[m
A
(x
)Lm
R
(x,y
)].
Обозначение: B = A·R.
Пример:
Пусть X = {x 1 , x 2 , x 3 }, Y = {y 1 , y 2 , y 3 , y 4 } и заданы нечеткое отношение
XRY = |
y 1 | y 2 | y 3 | y 4 |
| x 1 | 0,8 | 1 | 0 | 0,3 |
| x 2 | 0,8 | 0,3 | 0,8 | 0,2 |
| x 3 | 0,2 | 0,3 | 0 | 0,4 |
и нечеткое множество A = {0,3/x 1 ,0,7/x 2 ,1/x 3 }.
Проведем операцию L для А и столбца y 1 :
|
L |
|
= |
|
= |
|
После выполнения операции V на элементах полученного столбца имеем:
m B (y 1 ) = 0,3V0,7V0,2 = 0,7.
Проделав аналогичные вычисления для y 2 , y 3 , y 4 имеем:
m B (y 2 ) = 0,3
m B (y 3 ) = 0,7
m B (y 4 ) = 0,4.
И окончательно:
| A | R | B | |||||||||||||||||||||
|
· |
|
= |
|
Замечание. При заданном R, если А индуцирует В, то ближайшее четкое подмножество А индуцирует В .
Нечеткие подмножества последовательно обуславливающие друг друга
Если
А1 индуцирует А2 посредством R1 ,
А2 индуцирует А3 посредством R2 ,
.............................................
Аn-1 индуцирует Аn посредством Rn-1 ,
то
А1 индуцирует Аn посредством Rn-1 · Rn-2 · ...·R1 ,
где Rn-1 ·Rn-2 · ... ·R1 - определенная выше композиция нечетких отношений R1 , R2 , ..., Rn .
Пример:
Вернемся к примеру (max-min)-композиции.
| R1 | · | R2 | = | R1 ·R2 | ||||||||||||||||||||||||||||||||||||||||||
|
|
|
Пусть А={0,3/x 1 , 0,7/x 2 }, тогда
| А1 | R1 | А2 | |||||||||||||
|
· |
|
= |
|
| А2 | R2 | А3 | |||||||||||||||||||||
|
· |
|
= |
|
| А1 | R1 ·R2 | А3 | ||||||||||||||||
|
· |
|
= |
|
Немного о бинарных отношениях вида XRX
Нечеткие отношения вида XRX задаются функцией принадлежности mR (x,y ), но с условием, что x и y - элементы одного и того же универсального множества. В зависимости от своих свойств (основные - симметричность, рефлексивность, транзитивность) конкретные нечеткие отношения задают отношения сходства и различия, порядка или слабого порядка между элементами Х . Они имеют обширную сферу приложений в задачах автоматической классификации и принятия решений (сравнение альтернатив).
3. НЕЧЕТКАЯ И ЛИНГВИСТИЧЕСКАЯ ПЕРЕМЕННЫЕ
Понятие нечеткой и лингвистической переменных используется при описании объектов и явлений с помощью нечетких множеств.
Нечеткая переменная характеризуется тройкой <a, X, A>, где
a - наименование переменной,
X - универсальное множество (область определения a),
A - нечеткое множество на X, описывающее ограничения (т.е. mA (x )) на значения нечеткой переменной a.
Лингвистической переменной называется набор <b ,T,X,G,M>, где
b - наименование лингвистической переменной;
Т - множество ее значений (терм-множество), представляющих собой наименования нечетких переменных, областью определения каждой из которых является множество X. Множество T называется базовым терм-множеством лингвистической переменной;
G - синтаксическая процедура, позволяющая оперировать элементами терм-множества T, в частности, генерировать новые термы (значения). Множество TÈ G(T), где G(T) - множество сгенерированных термов, называется расширенным терм-множеством лингвистической переменной;
М - семантическая процедура, позволяющая превратить каждое новое значение лингвистической переменной, образуемое процедурой G, в нечеткую переменную, т.е. сформировать соответствующее нечеткое множество.
Замечание. Чтобы избежать большого количества символов
символ b используют как для названия самой переменной, так и для всех ее значений;
пользуются одним и тем же символом для обозначения нечеткого множества и его названия, например терм "молодой ", являющийся значением лингвистической переменной b = "возраст ", одновременно есть и нечеткое множество М ("молодой ").
Присвоение нескольких значений символам предполагает, что контекст позволяет разрешить возможные неопределенности.
Пример: Пусть эксперт определяет толщину выпускаемого изделия с помощью понятий "малая толщина ", "средняя толщина " и "большая толщина ", при этом минимальная толщина равна 10 мм, а максимальная - 80 мм.
Формализация такого описания может быть проведена с помощью следующей лингвистической переменной <b, T, X, G, M>, где
b - толщина изделия;
T - {"малая толщина ", "средняя толщина ", "большая толщина "};
X - [10, 80];
G - процедура образования новых термов с помощью связок "и ", "или " и модификаторов типа "очень ", "не ", "слегка " и др. Например: "малая или средняя толщина ", "очень малая толщина " и др.;
М - процедура задания на X = [10, 80] нечетких подмножеств А1
="малая толщина
", А2
= "средняя толщина
", А3
="большая толщина
", а также нечетких множеств для термов из G(T) в соответствии с правилами трансляции нечетких связок и модификаторов "и
", "или
", "не
", "очень
", "слегка
" и др. операции над нечеткими множествами вида: А Ç В, АÈ В, ![]() , CON А = А2
, DIL А = А0,5
и др.
, CON А = А2
, DIL А = А0,5
и др.
Замечание. Наряду с рассмотренными выше базовыми значениями лингвистической переменной "толщина " (Т={"малая толщина ", "средняя толщина ", "большая толщина "}) возможны значения, зависящие от области определения Х. В данном случае значения лингвистической переменной "толщина изделия" могут быть определены как "около 20 мм ", "около 50 мм ", "около 70 мм ", т.е. в виде нечетких чисел .
Продолжение примера:
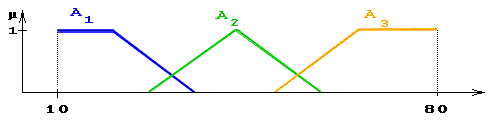
Функции принадлежности нечетких множеств:
"малая толщина" = А1 , "средняя толщина "= А2 , " большая толщина "= А3 .
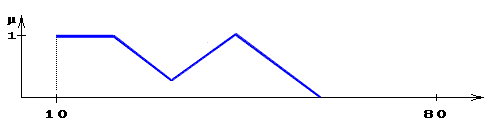
Функция принадлежности:
нечеткое множество "малая или средняя толщина " = А1 ÈА1 .
Нечеткие числа
Нечеткие числа - нечеткие переменные, определенные на числовой оси, т.е. нечеткое число определяется как нечеткое множество А на множестве действительных чисел R с функцией принадлежности mA (x )Î[0,1], где x - действительное число, т.е. x Î R.
Нечеткое число А нормально
, если ![]() mA
(x
)=1, выпуклое
, если для любых x£y£z выполняется
mA
(x
)=1, выпуклое
, если для любых x£y£z выполняется
mA (x )³mA (y )LmA (z ).
Множество a - уровня нечеткого числа А определяется как
Аa = {x /mA (x )³a}.
Подмножество SA ÌR называется носителем нечеткого числа А, если
S = {x /mA (x )>0}.
Нечеткое число А унимодально , если условие mA (x ) = 1 справедливо только для одной точки действительной оси.
Выпуклое нечеткое число А называется нечетким нулем , если
mA
(0) = ![]() (mA
(x
)).
(mA
(x
)).
Нечеткое число А положительно , если "x Î SA , x >0
и отрицательно , если "x Î SA , x <0.
Операции над нечеткими числами
Расширенные бинарные арифметические операции (сложение, умножение и пр.) для нечетких чисел определяются через соответствующие операции для четких чисел с использованием принципа обобщения следующим образом.
Пусть А и В - нечеткие числа, и ![]() - нечеткая операция, соответствующая операции
- нечеткая операция, соответствующая операции ![]() над обычными числами. Тогда
над обычными числами. Тогда
С = А![]() B ÛmC
(z
)=
B ÛmC
(z
)=![]() (mA
(x
)LmB
(y
))).
(mA
(x
)LmB
(y
))).
Отсюда:
С =![]() ÛmC
(z
)=
ÛmC
(z
)=![]() (mA
(x
)LmB
(y
))),
(mA
(x
)LmB
(y
))),
С = ![]() ÛmC
(z
)=
ÛmC
(z
)=![]() (mA
(x
)LmB
(y
))),
(mA
(x
)LmB
(y
))),
С = ![]() ÛmC
(z
)=
ÛmC
(z
)=![]() (mA
(x
)LmB
(y
))),
(mA
(x
)LmB
(y
))),
С = ![]() ÛmC
(z
)=
ÛmC
(z
)=![]() (mA
(x
)LmB
(y
))),
(mA
(x
)LmB
(y
))),
С = ![]() ÛmC
(z
)=
ÛmC
(z
)=![]() (mA
(x
)LmB
(y
))),
(mA
(x
)LmB
(y
))),
С = ![]() ÛmC
(z
)=
ÛmC
(z
)=![]() (mA
(x
)LmB
(y
))).
(mA
(x
)LmB
(y
))).
Нечеткие числа (L-R)-типа
Нечеткие числа (L-R)-типа - это разновидность нечетких чисел специального вида, т.е. задаваемых по определенным правилам с целью снижения объема вычислений при операциях над ними.
Функции принадлежности нечетких чисел (L-R)-типа задаются с помощью невозрастающих на множестве неотрицательных действительных чисел функций действительного переменного L(x ) и R(x ), удовлетворяющих свойствам:
а) L(-x )=L(x ), R(-x )=R(x );
б) L(0)=R(0).
Очевидно, что к классу (L-R) функций относятся функции, графики которых имеют следующий вид:
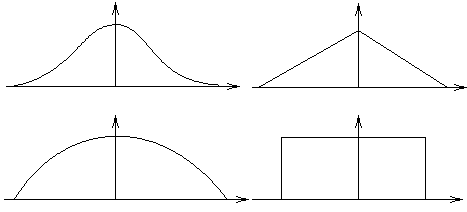
Примерами аналитического задания (L-R) функций могут быть
L(x
) = ![]() , p
³
0;
, p
³
0;
R(x
)= 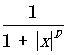 , p³ 0 и т.д.
, p³ 0 и т.д.
Пусть L(y ) и R(y ) - функции (L-R)-типа (конкретные). Унимодальное нечеткое число А с модой а (т.е. mA (a )=1) c помощью L(y ) и R(y ) задается следующим образом:
mA
(x
) = 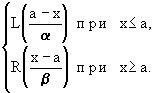
где а - мода; a>0, b>0 - левый и правый коэффициенты нечеткости.
Таким образом, при заданных L(y ) и R(y ) нечеткое число (унимодальное) задается тройкой А = (а , a, b).
Толерантное нечеткое число задается, соответственно, четверкой параметров А=(а 1 , a 2 , a, b), где а 1 и a 2 - границы толерантности, т.е. в промежутке [а 1 ,a 2 ] значение функции принадлежности равно 1.
Примеры графиков функций принадлежности нечетких чисел (L-R)-типа приведены ниже.
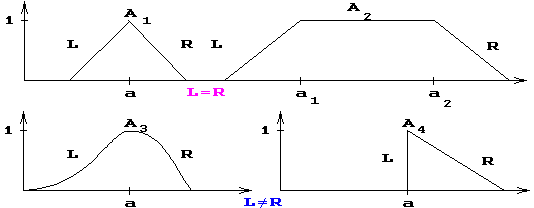
Мы не будем здесь рассматривать операции над (L-R) числами; отметим, что в конкретных ситуациях функции L(y ), R(y ), а также параметры a, b нечетких чисел (а , a, b) и (а 1 , a 2 , a, b ) должны подбираться таким образом, чтобы результат операции (сложения, вычитания, деления и т.д.) был точно или приблизительно равен нечеткому числу с теми же L(y ) и R(y ), а параметры a¢ и b¢ результата не выходили за рамки ограничений на эти параметры для исходных нечетких чисел, особенно если результат в дальнейшем будет участвовать в операциях.
Замечание. Решение задач математического моделирования сложных систем с применением аппарата нечетких множеств требует выполнения большого объема операций над разного рода лингвистическими и другими нечеткими переменными. Для удобства исполнения операций, а также для ввода-вывода и хранения данных, желательно работать с функциями принадлежности стандартного вида.
Нечеткие множества, которыми приходится оперировать в большинстве задач, являются, как правило, унимодальными и нормальными. Одним из возможных методов аппроксимации унимодальных нечетких множеств является аппроксимация с помощью функций (L-R)-типа.
Примеры (L-R)-представлений некоторых лингвистических переменных:
| Терм ЛП | (L-R)-представление | Графическое представление |
| Средний | А = (а , a, b)LR a = b>0 |
a b |
| Малый | А = (а , ¥, b)LR a = ¥ |
a = ¥b |
| Большой | А = (а , a, ¥)LR b=¥ |
ab = ¥ |
| Приблизительно в диапазоне | А = (а 1 , а 2 , a, ¥)LR a = b>0 |
ab a1 a2 |
| Определенный | А = (а , 0, 0)LR a = b = 0 |
a = 0 b = 0 |
Разнообразный зона полной неопределенности |
А = (а , ¥, ¥)LR a = b = ¥ |
a = b = ¥ |
4. НЕЧЕТКИЕ ВЫСКАЗЫВАНИЯ И НЕЧЕТКИЕ МОДЕЛИ СИСТЕМ
Нечеткими высказываниями будем называть высказывания следующего вида:
Высказывание <b есть b'>, где b - наименование лингвистической переменной, b' - ее значение, которому соответствует нечеткое множество на универсальном множестве Х.
Например высказывание <давление большое > предполагает, что лингвистической переменной "давление" придается значение "большое" , для которого на универсальном множестве Х переменной "давление" определено соответствующее данному значению "большое " нечеткое множество.
Высказывание <b есть mb'>, где m - модификатор, которому соответствуют слова "ОЧЕНЬ ", "БОЛЕЕ ИЛИ МЕНЕЕ ", "МНОГО БОЛЬШЕ " и др.
Например: <давление очень большое >, <скорость много больше средней > и др.
Составные высказывания, образованные из высказываний видов 1. и 2. и союзов "И ", "ИЛИ ", "ЕСЛИ .., ТО...", "ЕСЛИ.., ТО.., ИНАЧЕ ".
Высказывания на множестве значений фиксированной лингвистической переменной
То, что значения фиксированной лингвистической переменной соответствуют нечетким множествам одного и того же универсального множества Х, позволяет отождествлять модификаторы "очень " или "не " с операциями "CON" и "дополнение ", а союзы "И ", "ИЛИ " с операциями "пересечение " и "объединение " над нечеткими множествами .
Для иллюстрации понятия лингвистической переменной мы в качестве примера рассматривали лингвистическую переменную "толщина изделия " с базовым терм-множеством Т = {"малая ", "средняя ", "большая "}. При этом на Х = [10, 80] мы определили нечеткие множества А1 , А2 , А3 , соответствующие базовым значениям: "малая ", "средняя ", "большая ".
В этом случае высказыванию <толщина изделия очень малая
> соответствует нечеткое множество CONA = A2
; высказыванию <толщина изделия не большая или средняя
> - нечеткое множество А2
È![]() высказыванию <толщина изделия не малая и не большая
> А1
Ç
высказыванию <толщина изделия не малая и не большая
> А1
Ç![]() .
.
Высказывания <толщина изделия много больше средней
> или <толщина изделия близка к средней
> требуют использования нечетких отношений R ("много больше,чем
") и R ("близко к"), заданных на Х´Х. Тогда этим высказываниям будут соответствовать нечеткие множества A·R1
и A·R2
, индуцированные
29-04-2015, 02:39
