Случай двух и более лингвистических переменных
Пусть <a, Ta , X, Ga , Ma > и <b, Tb , Y, Gb , Mb > - лингвистические переменные, и высказываниям <a есть a'>, <b есть b '> соответствуют нечеткие множества А и В заданные на X и Y.
Составные нечеткие высказывания вида 3, связывающие значения лингвистических переменных a и b, можно привести к высказываниям вида 1, введя лингвистическую переменную (a, b), значениям которой будут соответствовать нечеткие множества на X´Y.
Напомним, что нечеткие множества А и В, заданные на X и Y, порождают на X´Y нечеткие множества ![]() и
и ![]() , называемые цилиндрическими продолжениями, с функциями принадлежности:
, называемые цилиндрическими продолжениями, с функциями принадлежности:
![]() (x,y
) = mA
(x
) при любом y
,
(x,y
) = mA
(x
) при любом y
,
![]() (x,y
) = mB
(y
) при любом x
,
(x,y
) = mB
(y
) при любом x
,
где (x,y ) X´Y.
Нечеткие множества, соответствующие составным высказываниям
<a есть a' и b есть b'> и
<a есть a' или b есть b'>,
определяются по следующим правилам (преобразования к виду 1), справедливым при условии невзаимодействия переменных, т.е. множества X и Y таковы, что их элементы не связаны какой-либо функциональной зависимостью.
Правила преобразований нечетких высказываний
Правило преобразования конъюнктивной формы
Справедливо выражение:
<a есть a' и b есть b'>Þ<(a, b) есть (a'Çb')>.
Здесь Þ - знак подстановки, a'Çb' - значение лингвистической переменной (a, b), соответствующее исходному высказыванию <a есть a' и b есть b'>, которому на X´Y ставится в соответствие нечеткое множество ![]() Ç
Ç![]() c функцией принадлежности
c функцией принадлежности
![]() (x,y
) =
(x,y
) = ![]() (x,y
)L
(x,y
)L![]() (x,y
) = mA
(x
)LmB
(y
).
(x,y
) = mA
(x
)LmB
(y
).
Правило преобразования дизъюнктивной формы
Справедливо выражение:
<a есть a' или b есть b'>Þ<(a,b) есть (a'Èb')>, где значению (a'Èb') лингвистической переменной (a, b) соответствует нечеткое множество ![]() È
È![]() , с функцией принадлежности
, с функцией принадлежности
![]() (x,y
) =
(x,y
) = ![]() (x,y
)V
(x,y
)V![]() (x,y
) = mA
(x
)VmB
(y
).
(x,y
) = mA
(x
)VmB
(y
).
Замечание 1. Правила справедливы также для переменных вида <a, T1 , X, G1 ,M1 > и <a, T2 , Y, G2 , M2 >, когда в форме значений лингвистических переменных формализованы невзаимодействующие характеристики одного и того же объекта. Например, для построения нечеткого множества высказывания <ночь теплая и очень темная > нужно использовать правило конъюнктивной формы, а для высказывания <ночь теплая или очень темная > - правило дизъюнктивной формы.
Замечание 2. Если задана совокупность лингвистических переменных {<ai , Ti , Xi , Gi , Mi >}, i = 1, 2, .., n , то любое составное высказывание, полученное из высказываний <a есть a'> с использованием модификаторов "очень ", "не ", "более или менее " и др. и связок "и ", "или ", можно привести к виду <a есть a'>, где a - составная лингвистическая переменная (a1 ,a2 ,..,an ), a' - ее значение, определяемое (как и функция принадлежности) в соответствии с вышеуказанными правилами.
Правило преобразования высказываний импликативной формы
Справедливо выражение:
<если a есть a', то b есть b'>Þ <(a, b) есть (a'®b')>, где значению (a'®b') лингвистической переменной (a, b) соответствует нечеткое отношение XRY на X´Y.
Функция принадлежности mR (x,y ) зависит от выбранного способа задания нечеткой импликации.
Способы определения нечеткой импликации
Будем считать, что заданы универсальные множества X и Y, содержащие конечное число элементов. Под способом определения нечеткой импликации "если А, то В" (где А и В нечеткие множества на X и Y соответственно) будем понимать способ задания нечеткого отношения R на X´Y, соответствующего данному высказыванию.
С целью обоснованного выбора определения нечеткой импликации, японскими математиками Мидзумото, Танака и Фуками было проведено исследование всех известных по литературе определений (плюс предложенные авторами). Рассмотренные определения задавали следующие нечеткие отношения для высказывания "если А, то В":
Rm
= (A´B)È(![]() ´Y)
´Y)
mRm (x,y ) = (mA (x )LmB (y )) V (1 - mA (x ));
Ra
= (![]() ´Y)Å(X´B)
´Y)Å(X´B)
mRa (x,y ) = 1 L (1-mA (x ) + mB (y ));
Rc = A´B
mRc (x,y ) = mA (x )LmB (y );
Rs
= A´Y![]() X´B
X´B
mRs
(x,y
) = 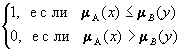 ;
;
Rg
= A´Y![]() X´B
X´B
mRg
(x,y
) = 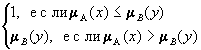 ;
;
Rsg
= ( A´Y![]() X´B ) Ç (
X´B ) Ç ( ![]() )
)
![]() ;
;
Rgg
= ( A´Y![]() X´B) Ç (
X´B) Ç (![]() )
)
![]() ;
;
Rgs
= ( A´Y![]() X´B) Ç (
X´B) Ç (![]() )
)
![]() ;
;
Rss
= ( A´Y![]() X´B) Ç (
X´B) Ç (![]() )
)
![]() ;
;
Rb
= (![]() ´Y)È(X´B)
´Y)È(X´B)
mRb (x,y) = (1-mA (x)) ÚmB (y);
Rà = A´Y![]() X´B
X´B
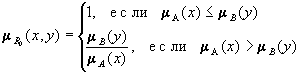 ;
;
R· = A´Y![]() X´B
X´B
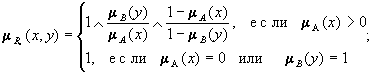
R*
= A´Y![]() X´B
X´B
mR* (x,y) = 1 - mA (x)+ mA (x)×mB (y);
R#
= A´Y![]() X´B
X´B
mR# (x,y)=( mA (x)ÙmB (y))Ú ((1 - mA (x)) Ù(1 - mB (y)) Ú(mB (y) Ù(1 - mA (x));
RÑ = A´Y![]() X´B
X´B
![]()
Правилом вывода являлось композиционное правило вывода с использованием (max-min)-композиции.
В качестве значений на входе системы рассматривались:
A' = A;
A' = "очень А"= А2 , mA 0,5 (x) = mA (x)2 ;
A' = "более или менее А" = А0,5 mA 0,5 (x)= mA (x)0,5 ;
A' = mA
(x)0,5
, ![]() (x) = 1 - mA
(x).
(x) = 1 - mA
(x).
Приведем таблицу итогов исследования. В ней символ "0" означает выполнение соответствующей схемы вход-выход, символ "x" - невыполнение. Следствие "неизвестно" (Н) соответствует утверждению: "если x=A, то нельзя получить никакой информации об y".
В данной таблице первая графа -"Посылка", вторая -"Следствие".
| 1 | 2 | Rm | Ra | Rc | Rs | Rg | Rsg | Rgg | Rgs | Rss | Rb | Rà | R· | R* | R# | RÑ |
| A | B | x | x | 0 | 0 | 0 | 0 | 0 | 0 | 0 | x | x | x | x | x | x |
| A2 | B2 | x | x | x | 0 | x | 0 | x | x | 0 | x | x | x | x | x | x |
| A2 | B | x | x | 0 | x | 0 | x | 0 | 0 | x | x | x | x | x | x | x |
| A0,5 | B0,5 | x | x | x | 0 | 0 | 0 | 0 | 0 | 0 | x | x | x | x | x | x |
| A0,5 | B | x | x | 0 | x | x | x | x | x | x | x | x | x | x | x | x |
| Н | 0 | 0 | x | 0 | 0 | x | x | x | x | 0 | 0 | 0 | 0 | x | x | |
| A | B | x | x | x | x | x | 0 | 0 | 0 | 0 | x | x | x | x | x | x |
Кроме ответа о выполнении соответствующей схемы (0 или х),авторами исследованы явные выражения для функций принадлежности следствий по каждому из вариантов определения нечеткой импликации, на основе чего ими был сформулирован вывод:
- Rm и Ra не могут быть использованы;
- Rc может использоваться частично; - Rs , Rg , Rsg , Rgg , Rgs , Rss рекомендованы к использованию;
- Rb , Rà, R·, R* , R# , RÑ не рекомендованы к использованию.
Логико-лингвистическое описание систем, нечеткие модели.
Логико-лингвистические методы описания систем основаны на том, что поведение исследуемой системы описывается на естественном (или близком к естественному) языке в терминах лингвистических переменных.
Входные и выходные параметры системы рассматриваются как лингвистические переменные, а качественное описание процесса задается совокупностью высказываний следующего вида:
L1 : если <A 1 > то <B 1 >,
L2 : если <A 2 > то <B 2 >,
....................
Lk : если <Ak > то <Bk >,
где <Ai >, i =1,2,..,k - составные нечеткие высказывания, определенные на значениях входных лингвистических переменных, а <Bi >, i = 1,2,..,k - высказывания, определенные на значениях выходных лингвистических переменных.
С помощью правил преобразования дизъюнктивной и конъюнктивной формы описание системы можно привести к виду:
L1 : если <A1 > то <B1 >,
L2 : если <A2 > то <B2 >,
....................
Lk : если <Ak > то <Bk >,
где A1 ,A2 ,..,Ak - нечеткие множества, заданные на декартовом произведении X универсальных множеств входных лингвистических переменных, а B1 , B2 , .., Bk - нечеткие множества, заданные на декартовом произведении Y универсальных множеств выходных лингвистических переменных.
Совокупность импликаций {L1 , L2 , ..., Lk } отражает функциональную взаимосвязь входных и выходных переменных и является основой построения нечеткого отношения XRY, заданного на произведении X´Y универсальных множеств входных и выходных переменных. Если на множестве X задано нечеткое множество A, то композиционное правило вывода B = A·R определяет на Y нечеткое множество B с функцией принадлежности
mB
(y
) =![]() (mA
(x
) LmR
(x,y
))
(mA
(x
) LmR
(x,y
))
Таким образом, композиционное правило вывода в этом случае задает закон функционирования нечеткой модели системы.
Рассмотрим широко цитируемый пример решения задачи нечеткого логического управления: построение модели управления паровым котлом.
Модель управления паровым котлом
Прототипом модели послужил паровой двигатель (лабораторный) с двумя входами (подача тепла, открытие дросселя) и двумя выходами (давление в котле, скорость двигателя).
Цель управления: поддержание заданного давления в котле (зависит от подачи тепла) и заданной скорости двигателя (зависит от открытия дросселя). В соответствии с этим, схема системы управления двигателем выглядит следующим образом:
Рассмотрим одну часть задачи - управление давлением.
Входные лингвистические переменные :
РЕ - отклонение давления (разность между текущим и заданным значениями);
СРЕ - скорость изменения отклонения давления.
Выходная лингвистическая переменная:
НС - изменение количества тепла.
Значения лингвистических переменных:
NB - отрицательное большое;
NM- отрицательное среднее;
NS- отрицательное малое;
NO- отрицательное близкое к нулю;
ZO- близкое к нулю;
PO - положительное близкое к нулю;
PS - положительное малое;
PM - положительное среднее;
PB - положительное большое.
Управляющие правила (15 правил), связывающие лингвистические значения входных и выходных переменных, имеют вид: "Если отклонение давления = Аi и, если скорость отклонения давления = Вi , то изменение количества подаваемого тепла равно Сi ", где Аi , Вi ,Сi - перечисленные выше лингвистические значения.
Полный набор правил задавался таблицей:
| ╬ | Отклонение давления РЕ |
Скорость изменения отклонения давления СРЕ |
Изменение количества подаваемого тепла НС |
| 1 | NB | NB или NM | PB |
| 2 | NB или NM | NS | PM |
| 3 | NS | PS или NO | PM |
| 4 | NO | PB или PM | PM |
| 5 | NO | NB или NM | NM |
| 6 | PO или ZO | NO | NO |
| 7 | PO | NB или NM | PM |
| 8 | PO | PB или PM | NM |
| 9 | PS | PS или NO | NM |
| 10 | PB или PM | NS | NM |
| 11 | PB | NB или NM | NB |
| 12 | NO | PS | PS |
| 13 | NO | NS | NS |
| 14 | PO | PS | PS |
| 15 | PO | PS | NS |
Лингвистические значения отклонений задавались нечеткими подмножествами на шкалах X, Y, Z следующей таблицей:
| -6 | -5 | -4 | -3 | -2 | -1 | 0 | +1 | +2 | +3 | +4 | +5 | +6 |
| PB | 0,3 | 0,7 | 1 | |||||||||
| PM | 0,3 | 0,7 | 1 | 0,7 | 0,3 | |||||||
| PS | 0,3 | 0,7 | 1 | 0,7 | 0,3 | |||||||
| PO | 0,3 | 1 | 0,7 | 0,3 | ||||||||
| NO | 0,3 | 0,7 | 1 | 0,3 | ||||||||
| NS | 0,3 | 0,7 | 1 | 0,7 | 0,3 | |||||||
| NM | 0,3 | 0,7 | 1 | 0,7 | 0,3 | |||||||
| NB | 1 | 0,7 | 0,3 |
То есть области значений входных переменных PE, CPE и выходной переменной НС представлялись 13 точками [-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6], равномерно расположенными между максимальными отрицательными и положительными значениями этих переменных.
Приведем управляющие правила к виду: "если (Аi ´ Вi ), то Сi ", где (Аi ´Вi ) декартово произведение нечетких множеств А и В , заданных на шкалах X и Y с функцией принадлежности
![]() (x,y
)= mAi
(x
)LmBi
(y
),
(x,y
)= mAi
(x
)LmBi
(y
),
определенной на X´Y.
Для каждого из правил вида "если (Аi ´Вi ), то Сi ", где (Аi ´Вi )- входное нечеткое множество, а Сi - соответствующее нечеткое значение выхода, определялось нечеткое отношение
Ri =(Аi ´Вi )´Сi , i = 1, 2, ..., 15
с функцией принадлежности
mRi ((x,y ),z )= (mAi (x )LmBi (y ))LmCi (z ).
Совокупности всех правил соответствовало нечеткое отношение
R = ![]() Ri
Ri
с функцией принадлежности
mR
(x,y,z
) = ![]() mRi
((x,y
),z
).
mRi
((x,y
),z
).
При заданных значениях А¢, В¢ входных переменных регулирующее значение С¢ входной переменной определялось на основе композиционного правила вывода:
С¢ = (А¢´В¢)![]() R,
R,
где ![]() - (max-min)-композиция.
- (max-min)-композиция.
Функция принадлежности С¢ имеет вид:
mC
¢(z
) = ![]()
![]() (mA
¢(x
) LmB
¢ (y
)) LmR
(x,y,z
).
(mA
¢(x
) LmB
¢ (y
)) LmR
(x,y,z
).
Числовое значение z
0
(изменение подаваемого тепла) определяется при этом либо из условия mC
¢(z
0
) = ![]() mC
¢
(z
),
mC
¢
(z
),
либо по формуле
z
0
= 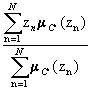 ,
,
где N - количество точек в Z (в данном случае N=13).
Задача управления скоростью двигателя решалась аналогично. Результаты практического использования показали, что разработанная нечеткая модель управления сравнима с классическими моделями оптимального управления.
Появление первых работ по построению моделей нечеткого логического управления для конкретных систем определило ряд общих вопросов, касающихся логических основ моделей, в их числе:
о полноте и непротиворечивости совокупности правил управления;
об адекватности представления правил управления вида "если А, то В " нечеткими отношениями, определяемыми разными способами;
о правильности способа вывода, основанного на (max-min)-композиции и возможности использования других видов операции композиции.
Полнота и непротиворечивость правил управления
Наиболее часто требование полноты для системы "если Аi , то Вi ", i =1,2,..,n , сводится к
X = ![]() Supp Ai
,
Supp Ai
,
где Supp Ai - носитель нечеткого множества Ai . Содержательно это означает, что для каждого текущего состояния х процесса существует хотя бы одно управляющее правило, посылка которого имеет ненулевую степень принадлежности для х .
Непротиворечивость системы управляющих правил чаще всего трактуется как отсутствие правил, имеющих сходные посылки и различные или взаимоисключающие следствия.
Степень непротиворечивости i -го и k -го правил можно задавать величиной
Cik
= |![]() (mAi
(x
)LmAk
(x
)) -
(mAi
(x
)LmAk
(x
)) - ![]() (mBi
(y
)LmBk
(y
))|.
(mBi
(y
)LmBk
(y
))|.
Суммируя по k , получаем оценку непротиворечивости i -го правила в системе:
Ci
= ![]() Cik
, 1<i
<N
, k
¹
i
.
Cik
, 1<i
<N
, k
¹
i
.
Если эта оценка превосходит некоторое пороговое значение, то правило из системы удаляется. В частности, для рассматриваемой выше модели управляющей системы парового котла, оценки степеней непротиворечивости равны:
| ╬ правила | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Ci | 2,4 | 3,4 | 4,2 | 3,8 | 4,2 | 1,8 | 4,5 | 3,5 | 4,0 | 3,9 | 1,7 | 3,3 | 4,1 | 3,7 | 3,3 |
Таким образом, при пороговом значении g=3 в модели остается всего три правила 1, 6 и 11.
Литература
Заде Л.А. Понятие лингвистической переменной и его применение к принятию приближенных решений. М.:Мир, 1976.
Кофман А. Введение в теорию нечетких множеств. М.: Радио и связь, 1982.
Нечеткие множества в моделях управления и искусственного интеллекта /Под ред. Д.А. Поспелова. М., 1986.
Прикладные нечеткие системы /Под ред. Тэтано Т., Асаи К., Сугэно М: Мир, 1993.
Нечеткие множества и теория возможностей. Последние достижения / Под ред. Р.Ягера М.: Радио и связь, 1986.
Орловский С.А. Проблемы принятия решений при нечеткой исходной информации. М.: Наука, 1981.
Борисов А.Н., Крумберг О.А., Федоров И.П. Принятие решений на основе нечетких моделей. Примеры использования. Рига:/ "Зинатне", 1990.
Малышев Н.Г., Берштейн Л.С., Боженюк А.В. Нечеткие модели для экспертных систем в САПР. М.: Энергоатомиздат, 1991.
Мелихов А.Н., Бернштейн Л.С., Коровин С.Я. Ситуационные советующие системы с нечеткой логикой. М.: Наука, 1990.
Р.Беллман, Л.Заде. Вопросы принятия решений в расплывчатых условиях // Вопросы анализа и процедуры принятия решений. / М.: Мир,1976.
29-04-2015, 02:39
