Аннотация
Данная работа посвящена построению и исследованию динамической модели портального манипулятора, описывающей переходные процессы в манипуляторе с шаговым приводом в момент его позиционирования. При построении были использованы экспериментально полученные параметры, благодаря чему удалось получить достаточно простую и адекватную модель.
При составлении подобных моделей у разработчика возникает стремление как можно более полно отразить свойства и характеристики объекта, что приводит к чрезмерному росту сложности модели, в результате чего снижается ее практическая полезность. Поэтому в данной работе особое внимание уделено разумному упрощению модели, а также возможности ее практического использования.
В ходе исследования полученной модели решена задача выбора оптимальной скорости перемещения рабочего органа, определена степень влияния точности позиционирования на быстродействие манипулятора.
Полученные результаты исследований могут быть использованы при проектировании новых и эксплуатации имеющихся моделей манипуляторов для определения рациональных значений динамических параметров.
Дипломная работа содержит:
пояснительная записка: 91 лист, 18 рисунков, 12 таблиц, 8 чертежей формата A1, 11 источников.
The Summary
The given work is devoted to development and research of dynamic model of the portal manipulator describing transient processes in the manipulator with a step-by-step drive at the moment of its positioning. At development, the experimentally obtained parameters were use, due to what it was possible to obtain simple enough and adequate model.
At development of similar models the developer has aspiration as it is possible more full to reflect properties and characteristics of object, that results in excessive growth of complexity of model, as a result of it its practical utility is reduced. Therefore, in the given work the special attention is give to reasonable simplification of model, and opportunity of its practical use.
During research of the received model the task of a choice of optimum speed of moving of a working body is solve, the degree of influence of accuracy of positioning on speed of the manipulator is determined.
The obtained results of researches can be use at designing new and operation of available models of manipulators for definition of rational meanings of dynamic parameters.
The degree work contains:
Explanatory note: 91 sheets, 18 figures, 12 tables, 8 drawings of a format A1, 11 sources.
Содержание
| Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 12 |
| 1.Моделирование динамики манипулятора . . . . . . . . . . . . . . . . . . . . . . . | 13 |
| 1.1 Методы построения динамической модели манипулятора . . . . . . . . | 13 |
| 1.2 Уравнения динамики манипулятора . . . . . . . . . . . . . . . . . . . . . . . . . . . | 15 |
| 2.Построение динамической модели переходных процессов манипулятора МРЛ-901П . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 19 |
| 2.1 Модель переходных процессов в манипуляторе МРЛ-901П . . . . . . . | 19 |
| 2.2 Анализ переходных процессов в манипуляторе МРЛ-901П . . . . . . . | 29 |
| 2.3 Определение жесткости звеньев манипулятора МРЛ-901П . . . . . . . . | 34 |
| 2.4 Исследование быстроходности манипулятора . . . . . . . . . . . . . . . . . . | 37 |
| 2.5 Методика проведения эксперимента по определению механических характеристик манипулятора МРЛ-901П . . . . . . . . . . | 41 |
| 2.6 Сравнение результатов расчета модели с экспериментальными данными . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 44 |
| 3.Оптимизация скорости перемещения рабочего органа манипулятора . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 45 |
| 3.1 Время перемещения рабочего органа манипулятора . . . . . . . . . . . . . | 45 |
| 3.2 Время перемещения рабочего органа манипулятора при малых расстояниях между рабочими точками . . . . . . . . . . . . . . . . . . . . . . . . | 49 |
| 3.3 Получение оптимальной скорости в момент выхода на конечную точку . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 52 |
| 4. Программные средства для исследования динамической модели портального манипулятора . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 54 |
| 4.1Программа для вычисления параметров переходного процесса портального манипулятора . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 54 |
| 4.2 Программа для вычисления времени переходного процесса и оптимальной скорости . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 56 |
| 5. Экономика и организация производства . . . . . . . . . . . . . . . . . . . . . . . . | 57 |
| 5.1 Организация и планирование НИР и ОКР . . . . . . . . . . . . . . . . . . . . . . | 57 |
| 5.1.1 Классификация и этапы НИР . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 57 |
| 5.1.2 Особенности управления созданием НТП в условиях рынка . . | 59 |
| 5.1.3 Характеристика инновационного процесса в современных условиях . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 61 |
| 5.1.4 Формы финансирования НИР и ОКР в условиях рынка . . . . . . | 65 |
| 5.1.5 Правовая защита производителей НТП . . . . . . . . . . . . . . . . . . . . | 68 |
| 5.2 Расчет экономического эффекта от внедрения методов расчета переходных процессов в портальном манипуляторе . . . . . . . . . . . . . | 69 |
| 5.2.1 Расчет капитальных затрат . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 70 |
| 5.2.2 Расчет эксплуатационных затрат . . . . . . . . . . . . . . . . . . . . . . . . . | 80 |
| 5.2.3 Расчет условно-годового экономического эффекта и срока окупаемости . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 84 |
| Заключение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 86 |
| Литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 87 |
| Приложение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 88 |
Введение
Для решения задачи выбора оптимальной скорости перемещения звеньев манипулятора с шаговым двигателем, с целью увеличения его быстродействия, необходимо учитывать переходные процессы возникающие при позиционировании рабочих органов. Переходные процессы в виде затухающих механических колебаний возникают под действием инерционных нагрузок и приводят к увеличению времени позиционирования при выполнении переходов технологического процесса, например, при сборке, сверлении, контроле и др. Для планирования траектории необходимо знать время затухания колебаний до значения допустимой погрешности позиционирования, при котором рабочий орган манипулятора может продолжать движение. С целью определения времени такого переходного процесса создана модель манипулятора портального типа с консольной подвижной частью.
- Моделирование динамики манипулятора
- Методы построения динамической модели манипулятора
Динамическая модель манипулятора может быть построена на основе использования известных законов ньютоновской или лагранжевой механики. Результатом применения этих законов являются уравнения, связывающие действующие в сочленениях силы и моменты с кинематическими характеристиками и параметрами движения звеньев. Таким образом, уравнения динамики движения реального манипулятора могут быть получены традиционными методами Лагранжа – Эйлера или Ньютона – Эйлера. С помощью этих двух методов получен ряд различных форм уравнения движения, эквивалентных в том смысле, что они описывают динамику движения одной и той же физической системы.
Вывод уравнений динамики движения манипулятора методом Лагранжа – Эйлера отличается простотой и единством подхода. В рамках предположения о том, что звенья представляют собой твердые тела, этот подход приводит в общем случае к системе нелинейных дифференциальных уравнений второго порядка. Уравнения Лагранжа – Эйлера обеспечивают строгое описание динамики состояния манипулятора и могут быть использованы для разработки усовершенствованных законов управления в пространстве присоединенных переменных. В меньшей степени они используются для решения прямой и обратной задач динамики. Прямая задача состоит в том, чтобы по заданным силам и моментам определить обобщенные ускорения, интегрирование которых позволяет получить значения обобщенных координат и скоростей. Обратная задача динамики заключается в том, чтобы по заданным обобщенным координатам, скоростям и ускорениям определить действующие в сочленениях манипулятора силы и моменты.
С целью получения более эффективных с вычислительной точки зрения алгоритмов можно использовать уравнения Ньютона – Эйлера. Вывод уравнений движения манипулятора методом Ньютона – Эйлера прост по содержанию, но весьма трудоемок. Результатом является система прямых и обратных рекуррентных уравнений, последовательно применяемых к звеньям манипулятора. С помощью прямых уравнений последовательно от основания к схвату вычисляются кинематические характеристики движения звеньев, такие, как линейные и угловые скорости и ускорения, линейные ускорения центров масс звеньев. Обратные уравнения позволяют последовательно от схвата к основанию вычислить силы и моменты, действующие на каждое из звеньев. Наиболее важный результат такого подхода состоит в том, что время, необходимое для вычисления обобщенных сил и моментов прямо и пропорционально числу сочленений, но не зависит от реализующейся в процессе движения конфигурации манипулятора. Это позволяет реализовывать простые законы управления манипулятором в реальном времени.
Низкая вычислительная эффективность уравнений Лагранжа – Эйлера обусловлена в основном тем, что для описания кинематической цепи используются матрицы преобразования однородных координат. Уравнения Ньютона – Эйлера обладают большей вычислительной эффективностью, что связано с их рекуррентной природой. Однако такие рекуррентные уравнения не обладают “аналитичностью”, столь полезной при синтезе управления в пространстве состояний. Для синтеза законов управления желательно иметь в распоряжении замкнутую систему дифференциальных уравнений, точно описывающих динамику движения манипулятора.
В связи с тем что для построения модели динамики переходных процессов и дальнейшего анализа полученных уравнений необходима аналитическая форма, решено использовать для получения уравнений динамики метод Лагранжа – Эйлера.
- Уравнения динамики манипулятора
Уравнения Лагранжа второго рода для голономной системы с n
степенями свободы, которым отвечают обобщенные координаты ![]() (j =
1,2,…,n
), имеют вид
(j =
1,2,…,n
), имеют вид
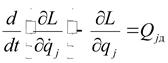 (j =
1,2,…,n
), (j =
1,2,…,n
), |
(1.1) |
где ![]() – функция Лагранжа, разности кинетической Т
и потенциальной П
энергий системы;
– функция Лагранжа, разности кинетической Т
и потенциальной П
энергий системы; ![]() – обобщенные силы управляющих приводов, приведенные к j
-ой обобщенной координате: они имеют размерность моментов, если
– обобщенные силы управляющих приводов, приведенные к j
-ой обобщенной координате: они имеют размерность моментов, если ![]() – угол поворота, или сил, если
– угол поворота, или сил, если ![]() – линейное перемещение.
– линейное перемещение.
С учетом того, что ![]() и
и ![]() , перепишем уравнение (1.1) в виде
, перепишем уравнение (1.1) в виде
 , , |
(1.2) |
где ![]() ,
, ![]() .
.
В последних равенствах через ![]() обозначены внешние обобщенные силы, вызванные весом звеньев и груза, удерживаемого в захватном устройстве. При наличии внешнего воздействия – силы
обозначены внешние обобщенные силы, вызванные весом звеньев и груза, удерживаемого в захватном устройстве. При наличии внешнего воздействия – силы ![]() , приложенной к захватному устройству, в правую часть равенства для
, приложенной к захватному устройству, в правую часть равенства для ![]() надо добавить член
надо добавить член ![]() , характеризующий это воздействие:
, характеризующий это воздействие:
| (1.3) |
Используем выражение (1.2) для вывода уравнений динамики манипулятора. Рассматривая исполнительный механизм манипулятора как систему из n твердых тел, запишем его кинетическую энергию T в виде суммы кинетических энергий звеньев:
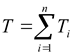 . . |
(1.4) |
В свою очередь величину ![]() определим по формуле [3]
определим по формуле [3]
| (1.5) |
где ![]() – масса звена i
;
– масса звена i
; ![]() – скорость некоторой точки звена
– скорость некоторой точки звена ![]() , принятой за полюс;
, принятой за полюс; ![]() – вектор радиус центра инерции звена в системе осей с ним связанных, начало которой совпадает с полюсом
– вектор радиус центра инерции звена в системе осей с ним связанных, начало которой совпадает с полюсом ![]() ;
; ![]() – тензор инерции звена в точке
– тензор инерции звена в точке ![]() ;
; ![]() – вектор угловой скорости звена в принятой системе координат.
– вектор угловой скорости звена в принятой системе координат.
Выражение (1.5) принимает наиболее простой вид, если за полюс звена принять его центр инерции; величина ![]() будет равна нулю и выражение (1.5) упростится:
будет равна нулю и выражение (1.5) упростится:
| (1.6) |
Кроме того, в большинстве случаев звенья манипулятора представляют собой твердые тела, обладающие симметрией относительно трех ортогональных осей, проведенных через центр инерции. Напомнив правило разметки осей систем координат, связанных со звеньями, в соответствии с которым одна из осей системы ![]() совпадает с осью звена (вектором
совпадает с осью звена (вектором ![]() ), а две другие образуют с ней правую триаду, получим при помещении точки
), а две другие образуют с ней правую триаду, получим при помещении точки ![]() в центр инерции
в центр инерции ![]() (см. рис. 1.1) оси полученной системы
(см. рис. 1.1) оси полученной системы ![]() становятся главными осями инерции и тензор вектора в точке
становятся главными осями инерции и тензор вектора в точке ![]() имеет вид диагональной матрицы
имеет вид диагональной матрицы
 , , |
(1.7) |
моменты инерции относительно осей в которой определяются выражениями
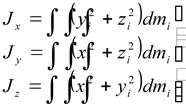 , , |
(1.8) |
и для звеньев заданной конфигурации являются известными константами. При отсутствии осевых симметрий тензор инерции звена в точке ![]() характеризуется матрицей
характеризуется матрицей
 , , |
(1.9) |
центробежные моменты в которой определяются выражениями
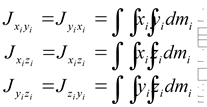 |
(1.10) |
и также являются известными константами.
Определим вектор скорости центра инерции звена i через проекции на оси связанной с ним системы координат как
| (1.11) |
или через проекции на оси неподвижной системы осей в виде
| (1.12) |
По аналогии с ![]() введем вектор угловой скорости
введем вектор угловой скорости
29-04-2015, 04:09
