| (1.13) |
и запишем равенство (1.6) в развернутой форме для случая, когда звенья манипулятора обладают симметрией относительно главных осей инерции. Для этого подставим выражения ![]() ,
, ![]() ,
, ![]() из (1.7), (1.11), (1.13) в (1.6) и получим
из (1.7), (1.11), (1.13) в (1.6) и получим
| (1.14) |
При использовании вектора скорости центра инерции в форме (1.14) выражение
| (1.15) |
с учетом которого равенство (1.4) принимает вид
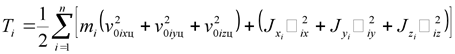 . . |
(1.16) |
- Построение динамической модели переходных процессов манипулятора МРЛ-901П
2.1 Модель переходных процессов в манипуляторе МРЛ-901П
М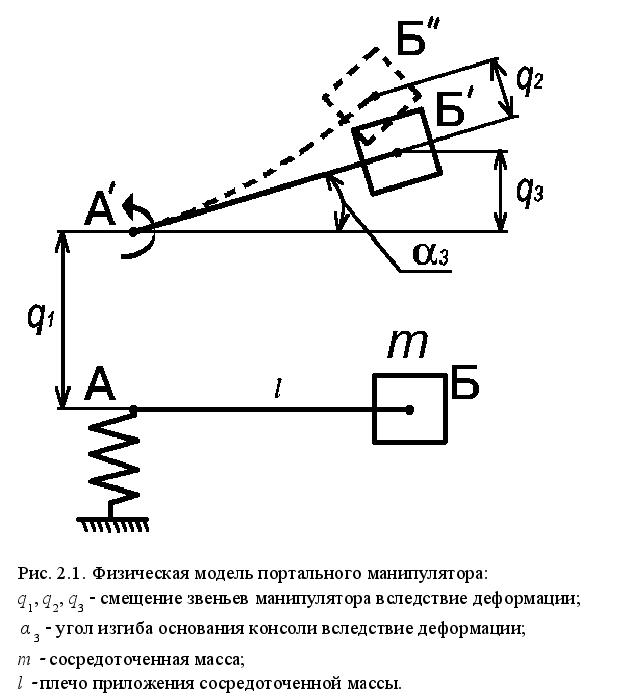
одель портального манипулятора МРЛ-901П представлена на рис. 2.1. Деформирующимися элементами в манипуляторе являются: зубчатый ремень, обозначенный пружиной; консольная часть, на которой имеется сосредоточенная масса m
. Деформация поперечной консоли обозначена на схеме углом ![]() . Исходными данными для расчета такой модели будут: значение подвижной массы m
, плечо приложения этой массы l
, а также коэффициент натяжения зубчатого ремня, определяемый как отношение прогиба ремня к его длине и влияющий на жесткость, и демпфирование модуля линейного перемещения.
. Исходными данными для расчета такой модели будут: значение подвижной массы m
, плечо приложения этой массы l
, а также коэффициент натяжения зубчатого ремня, определяемый как отношение прогиба ремня к его длине и влияющий на жесткость, и демпфирование модуля линейного перемещения.
При остановке электроприводов подвижные массы будут продолжать движение под действием инерционных сил, в результате чего точки А и Б займут положение ![]() и
и ![]() соответственно, затем остановятся и под действием сил упругой деформации пружины и балки начнут совершать колебательное движения.
соответственно, затем остановятся и под действием сил упругой деформации пружины и балки начнут совершать колебательное движения.
Рассматриваемая модель имеет три степени свободы, обозначим независимые обобщенные координаты как ![]() ,
, ![]() и
и ![]() . Для описания данной модели воспользуемся уравнением Лагранжа второго рода:
. Для описания данной модели воспользуемся уравнением Лагранжа второго рода:
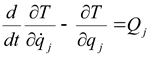 (j =
1,2,…,k
), (j =
1,2,…,k
), |
(2.1) |
где T - кинетическая энергия системы; Q - обобщенная сила; k - количество степеней свободы.
Кинетическая энергия системы с тремя степенями свободы является однородной квадратичной формой обобщенных скоростей [5]:
| (2.2) |
Коэффициенты ![]() являются функциями координат
являются функциями координат ![]() ,
, ![]() и
и ![]() .
.
Предположим, что обобщенные координаты отсчитываются от положения равновесия, где ![]() .
.
Располагая коэффициенты ![]() по степеням и пологая для упрощения записи
по степеням и пологая для упрощения записи ![]() , получим:
, получим:
| (2.3) |
Потенциальная энергия ![]() системы:
системы:
| (2.4) |
При этом учитываем, что в положении равновесия ![]() обобщенные силы также обращаются в нуль.
обобщенные силы также обращаются в нуль.
В (2.4) для упрощения приняты следующие обозначения:
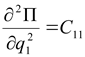 ,
, 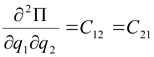 ,
, 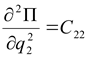 ,
, 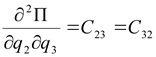 ,
, 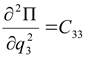 ,
, 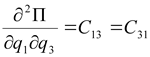 .
.
Для составления дифференциальных уравнений свободных колебаний в форме уравнений Лагранжа второго рода, выразим потенциальную энергию через обобщенные координаты. Рассмотрим равновесие системы, на которую действуют силы ![]()
![]() …,
…,![]() . Потенциальная энергия в состоянии устойчивого равновесия имеет минимум, равный нулю, а при вызванном действием сил
. Потенциальная энергия в состоянии устойчивого равновесия имеет минимум, равный нулю, а при вызванном действием сил ![]() отклонении от него выражается квадратичной формой вида (2.4).
отклонении от него выражается квадратичной формой вида (2.4).
Элементарная работа всех сил действующих на систему, по принципу возможных перемещений должна быть равна нулю:
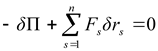 . . |
(2.5) |
Замечая, что
 |
а также приравнивая к нулю коэффициенты при независимых вариациях ![]() ,
, ![]() и
и ![]() , получаем три уравнения:
, получаем три уравнения:
 , , |
(2.6) |
Здесь ![]() ,
, ![]() и
и ![]() - обобщенные силы для системы сил
- обобщенные силы для системы сил ![]()
![]() …,
…,![]() , уравновешивающих потенциальные силы, возникающие при отклонении системы из положения равновесия
, уравновешивающих потенциальные силы, возникающие при отклонении системы из положения равновесия ![]() . Заменяя в (2.6) производные потенциальной энергии их выражениями согласно (2.4), получим систему уравнений, определяющих значение координат
. Заменяя в (2.6) производные потенциальной энергии их выражениями согласно (2.4), получим систему уравнений, определяющих значение координат ![]() ,
, ![]() и
и ![]() в положении равновесия:
в положении равновесия:
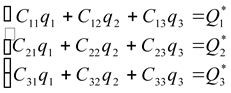 , , |
(2.7) |
причем ![]() ,
, ![]() и
и ![]() .
.
Решение системы (2.7) имеет вид:
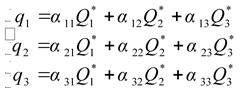 , , |
(2.8) |
где
 |
(2.9) |
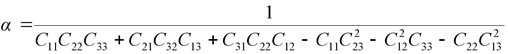 .
.
На систему действуют обобщенные силы, которыми являются инерционные силы и силы сопротивления движению. Обычно в сложных системах в целях упрощения [4, 5] силу сопротивления принимают пропорциональной первой степени скорости движения. С целью упрощения условимся, что угол ![]() мал и координаты массы m
можно записать как
мал и координаты массы m
можно записать как ![]() . Поэтому на основании кинетостатики можем записать:
. Поэтому на основании кинетостатики можем записать:
| (2.10) |
где ![]() - обобщенная сила,
- обобщенная сила, ![]() - коэффициент сопротивления пропорциональный первой степени скорости движения массы m
. Так как масса собственно консоли манипулятора МРЛ-901П меньше массы закрепленных на ней рабочих головок, захватов и деталей, для упрощения примем условие, что точка исследования колебаний (практически - рабочий орган манипулятора) совпадает с точкой приложения сосредоточенной массы m
.
- коэффициент сопротивления пропорциональный первой степени скорости движения массы m
. Так как масса собственно консоли манипулятора МРЛ-901П меньше массы закрепленных на ней рабочих головок, захватов и деталей, для упрощения примем условие, что точка исследования колебаний (практически - рабочий орган манипулятора) совпадает с точкой приложения сосредоточенной массы m
.
Сила ![]() действует на все звенья манипулятора следовательно:
действует на все звенья манипулятора следовательно:
| (2.11) |
Коэффициенты ![]() в (2.7) будем определять из того, что согласно (2.11) звенья можно рассматривать независимо друг от друга. Положим сначала, что
в (2.7) будем определять из того, что согласно (2.11) звенья можно рассматривать независимо друг от друга. Положим сначала, что ![]() действует только по координате
действует только по координате ![]() , затем только по координате
, затем только по координате ![]() и наконец только по координате
и наконец только по координате ![]() , тогда в выражение (2.7) можно переписать:
, тогда в выражение (2.7) можно переписать:
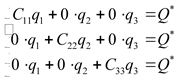 , , |
(2.12) |
таким образом ![]() , используя (2.9) находим:
, используя (2.9) находим:
 |
(2.13) |
Коэффициенты ![]() ,
, ![]() и
и ![]() определяют податливость звеньев манипулятора по координатам
определяют податливость звеньев манипулятора по координатам ![]() ,
, ![]() и
и ![]() соответственно. Выражая податливость звеньев через их жесткость, запишем:
соответственно. Выражая податливость звеньев через их жесткость, запишем:
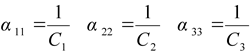 , , |
(2.14) |
где ![]() ,
, ![]() и
и ![]() жесткости звеньев по координатам
жесткости звеньев по координатам ![]() ,
, ![]() и
и ![]() соответственно.
соответственно.
Подставляя (2.14) , (2.11) и (2.10) в (2.8) получим:
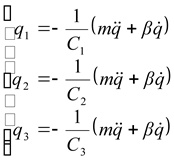 |
(2.15) |
Для решения этой системы нужно выразить скорость и ускорение массы m через их составляющие:
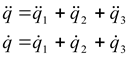 . . |
(2.16) |
Поскольку в манипуляторе суммарную жесткость удобно экспериментально определять, прикладывая соответствующее усилие к его рабочему органу, и так как в конечном итоге необходимо определить положение массы m
, координаты которой выражаются как ![]() , то для этого достаточно сложить уравнения в выражении (2.15):
, то для этого достаточно сложить уравнения в выражении (2.15):
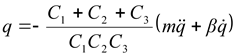 |
(2.17) |
или:
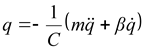 , , |
(2.18) |
где С - суммарная жесткость звеньев манипулятора.
Анализ показывает, что величина C является переменной и зависит от плеча приложения l сосредоточенной массы m .
Преобразуя (2.18), получаем уравнение описывающие переходный процесс в системе:
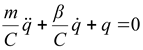 . . |
(2.19) |
Уравнение (2.19) легко решается классическим способом при следующих начальных условиях:
| (2.20) |
где ![]() - скорость рабочего органа манипулятора в момент выхода на конечную точку.
- скорость рабочего органа манипулятора в момент выхода на конечную точку.
Выражение (2.19) представляет собой линейное дифференциальное уравнение второго порядка. Будем искать частное решение уравнения в виде:
| (2.21) |
где ![]() и
и ![]() - произвольные постоянные, которые могут быть определены из начальных условий: при t
= 0;
- произвольные постоянные, которые могут быть определены из начальных условий: при t
= 0; ![]() и
и ![]() - корни характеристического уравнения:
- корни характеристического уравнения:
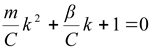 . . |
(2.22) |
Решение уравнения (2.22) будет иметь вид:
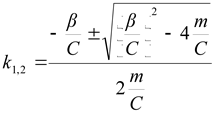 |
(2.23) |
Определим произвольные постоянные ![]() и
и ![]() , решая систему уравнений:
, решая систему уравнений:
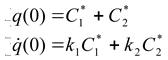 . . |
(2.24) |
Решение системы (2.24) будет иметь вид:
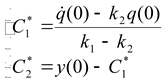 , , |
(2.25) |
если учесть (2.20) то:
 |
(2.26) |
подставляя (2.26) в (2.21) и с учетом (2.23) имеем:
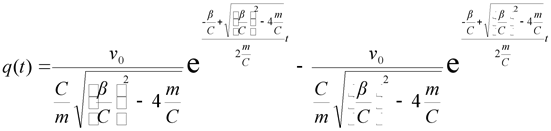 |
(2.27) |
где ![]() - реальная часть;
- реальная часть; 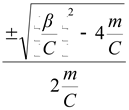 - мнимая часть.
- мнимая часть.
Тогда разделяя реальную и мнимую части в (2.27) получим:
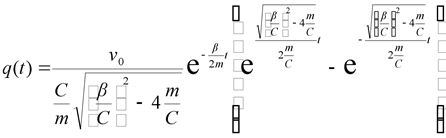 . . |
(2.28) |
Учитывая что:
| (2.29) |
имеем:
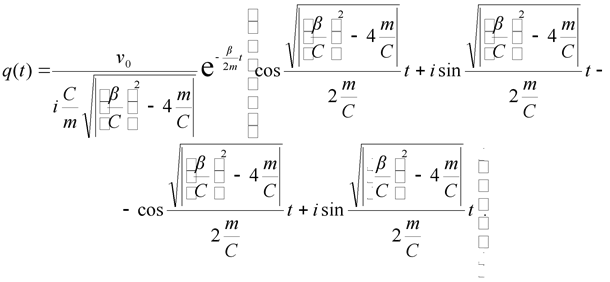 |
(2.30) |
Преобразуя (2.30) получим решение уравнения (2.19):
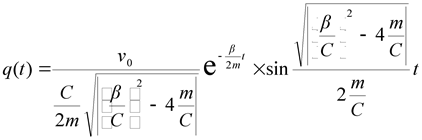 |
(2.31) |
Прологарифмируем выражение (2.31) предварительно подставив в него значение допустимой погрешности позиционирования:
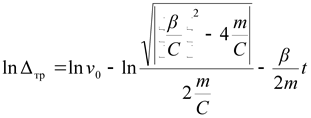 , , |
(2.32) |
где ![]() - допустимая погрешность позиционирования.
- допустимая погрешность позиционирования.
Преобразуя (2.32) получим выражение для определения времени переходного процесса:
 |
(2.33) |
Для расчета жесткости C
и коэффициента демпфирования ![]() в модели используются экспериментально полученные зависимости. В частности коэффициент демпфирования определяется по осциллограмме затухания колебаний рабочего органа.
в модели используются экспериментально полученные зависимости. В частности коэффициент демпфирования определяется по осциллограмме затухания колебаний рабочего органа.
Таким образом, время переходного процесса, для данного типа манипулятора при заданной массе положении рабочего органа определяется по выражению (2.33), в котором коэффициенты жесткости и демпфирования предварительно определены экспериментально.
2.2 Анализ переходных процессов в манипуляторе МРЛ-901П
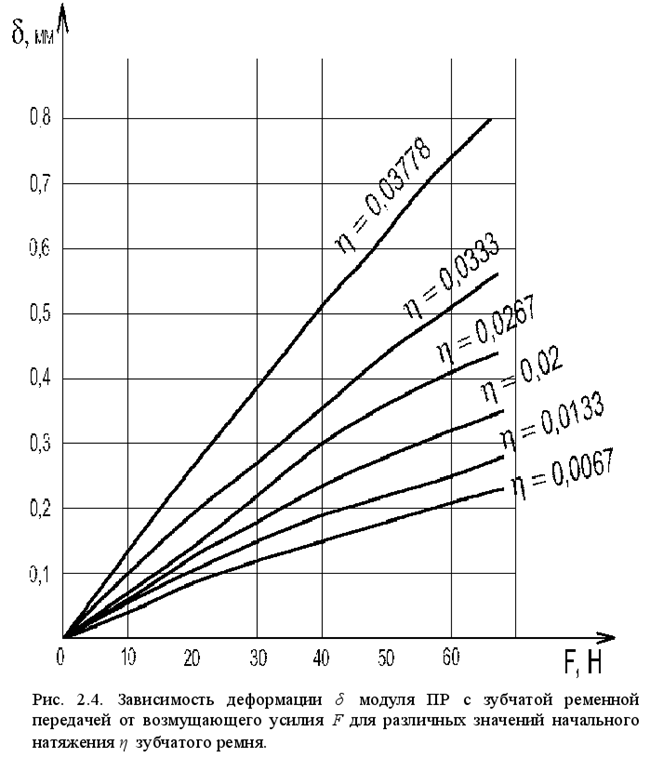
Источниками возникновения переходных процессов в манипуляторе МРЛ-901П являются: зубчатая ременная передача линейного модуля манипулятора и его свободная консоль.
На этапе зондирующих экспериментов исследовались парные зависимости коэффициента демпфирования от натяжения зубчатого ремня и смещения рабочего органа вдоль консоли. Результаты анализа полученных осциллограмм сведены в таблицы 2.1 и 2.2.
Анализ результатов показывает, что натяжение зубчатого ремня существенным образом влияет на коэффициенты демпфирования модуля линейного перемещения: так при увеличении начального натяжения ремня от минимального значения h = 0,03778 до максимального h = 0,00667 (в исследуемых приделах) коэффициент демпфирования уменьшается в 3 раза. Таким образом, можно сделать вывод о том, что демпфирование линейного модуля с зубчатой ременной передачей может задаваться и варьироваться в широких пределах, как на этапе конструирования, так и в процессе его эксплуатации.
| Табл. 2.1 | |||||
| Результаты анализа осциллограмм собственных колебаний рабочего органа манипулятора МРЛ-901П на консоли | |||||
| Величина смещения рабочего органа вдоль консоли ly , мм | Период колебаний рабочего органа T, с. | Частота колебаний w , с-1 | Логарифмический декремент затухания n | Коэффициент демпфирования b , кг/c | Время затухания колебаний tп.п., с. |
| 0 | 0,057 | 17,54 | 0,956 | 369 | 0,6 |
| 175 | 0,067 | 15 | 0,693 | 227,55 | 0,9 |
| 350 | 0,08 | 12,5 | 0,446 | 122,65 | 1,2 |
Анализ результатов исследований показывает, что смещение рабочего органа манипулятора МРЛ-901П вдоль свободной консоли, также как и
| Табл. 2.2 | ||||||||||
| Результаты исследований демпфирующих свойств модуля линейного перемещения с ременной передачей | ||||||||||
Номер опыта |
Номер параллельного опыта | Случайный порядок проведения | Степень начального натяжения | Период колебаний Т, с. |
Логарифмический декремент затухания n | Коэффициент демпфирования b , кг/c | Среднее время затухания | |||
| опытов | ремня h | парал-лельные опыты | среднее | парал-лельные опыты | среднее | парал-лельные опыты | среднее | колебаний tп.п. , с | ||
| 1 | 3 | 0,1 | 1,15 | 460,15 | ||||||
| 2 | 1 | 0,102 | 1,23 | 482,35 | ||||||
| 1 | 3 | 12 | 0,03778 | 0,113 | 0,105 | 1,383 | 1,253 | 489,72 | 477,33 | 0,4 |
| 4 | 7 | 0,108 | 1,258 | 465,91 | ||||||
| 5 | 11 | 0,102 | 1,244 | 488,52 | ||||||
| 1 | 4 | 0,125 | 0,85 | 272,12 | ||||||
| 2 | 15 | 0,128 | 0,815 | 254,68 | ||||||
| 2 | 3 | 10 | 0,02 | 0,117 | 0,12 | 0,756 | 0,8 | 258,3 | 266,67 | 0,45 |
| 4 | 9 | 0,115 | 0,79 | 275,08 | ||||||
| 5 | 14 | 0,115 | 0,789 | 273,17 | ||||||
| 1 | 6 | 0,12 | 0,486 | 162,11 | ||||||
| 2 | 5 | 0,12 | 0,493 | 164,25 | ||||||
| 3 | 3 | 3 | 0,0067 | 0,132 | 0,128 | 0,496 | 0,504 | 150,32 | 157,47 | 0,6 |
| 4 | 8 | 0,14 | 0,544 | 155,43 | ||||||
| 5 | 2 | 0,128 | 0,5 | 155,24 | ||||||
увеличение начального натяжения ремня, вызывает уменьшение коэффициентов демпфирования, что существенно (в 2…3 раза) увеличивает время полного затухания собственных колебаний рабочего органа (см. табл. 2.1 и 2.2), и, как следствие снижает реальную производительность.
Смещение рабочего органа относительно основания и увеличение натяжения ремня приводит также к уменьшению частоты собственных колебаний манипулятора, что должно учитываться при использовании его в технологических процессах, связанных с резонансными явлениями.
Комплексные исследования демпфирующих свойств манипулятора осуществлялись с целью установления численной зависимости коэффициента демпфирования от величины начального натяжения ремня и смещения рабочего органа вдоль консоли. В качестве функции отклика выбиралась линейная модель. База данных для построения плана экспериментов сведена в табл. 2.
Основные уровни и интервалы варьирования выбирались на основе результатов зондирующих экспериментов, а также исследований жесткости и точносных параметров манипулятора МРЛ-901П.
| Табл. 2.3 | ||||
| База данных для построения плана экспериментов | ||||
Наименование фактора |
Условное обозначение | Область определения | Основной уровень | Интервал варьирования |
| Начальное натяжение ремняh | X1 |
0...0,04 |
0,02 |
0,013 |
| Величина смещения рабочего органа манипулятора вдоль консоли ly , мм | X2 |
0...350 |
175 |
175 |
Матрица планирования и результаты экспериментов сведены в табл. 2.4.
Проводилась полная статистическая обработка результатов экспериментов, позволившая получить адекватную модель зависимости коэффициентов демпфирования от исследуемых факторов в виде:
| (2.34) |
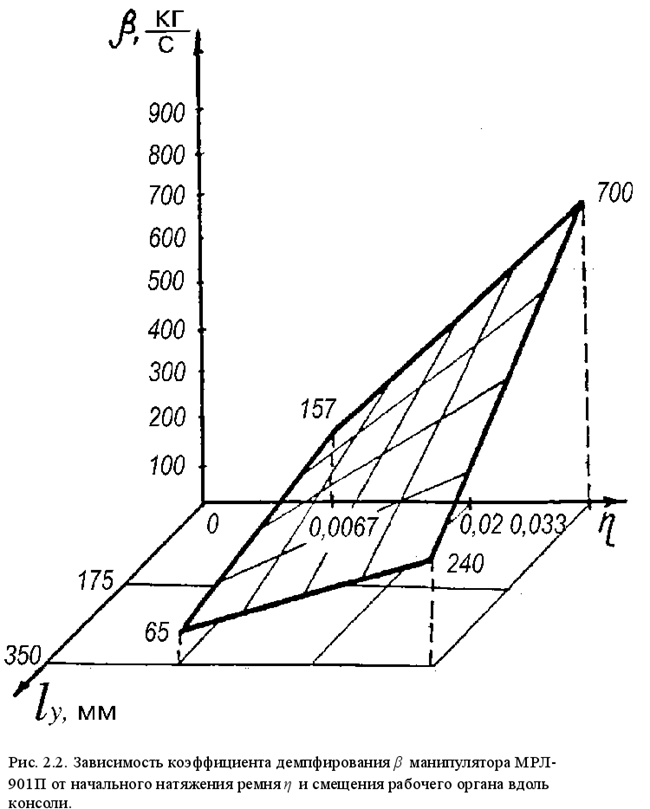
Поверхность отклика представлена на рис. 2.2. Выражение (2.34) позволяет получить численное значение коэффициента демпфирования, необходимое для расчета продолжительности переходного процесса при позиционировании.
| Табл. 2.4 | ||||||||
| Матрица планирования и результатов экспериментов по комплексному исследованию демпфирующих свойств манипулятора МРЛ-901П | ||||||||
Номер опыта |
|
|
|
|
Среднее значение коэффициента демпфирования, кг/c | Дисперсия среднего арифметического | Вычисленное значение | |
| 1 | +1 | +1 | +1 | +1 | 240 | 64 | 240 | |
| 2 | +1 | +1 | -1 | -1 | 700 | 49 | 700 | |
| 3 | +1 | -1 | +1 | -1 | 65 | 4 | 65 | |
| 4 | +1 | -1 | -1 | +1 | 157 | 16 | 157 | |
Экспериментальные исследования времени переходного процесса осуществлялись при помощи комплекта виброизмерительной аппаратуры АВ-44, вибродатчик которой крепился на рабочем органе манипулятора.
2.3 Определение жесткости звеньев манипулятора МРЛ-901П
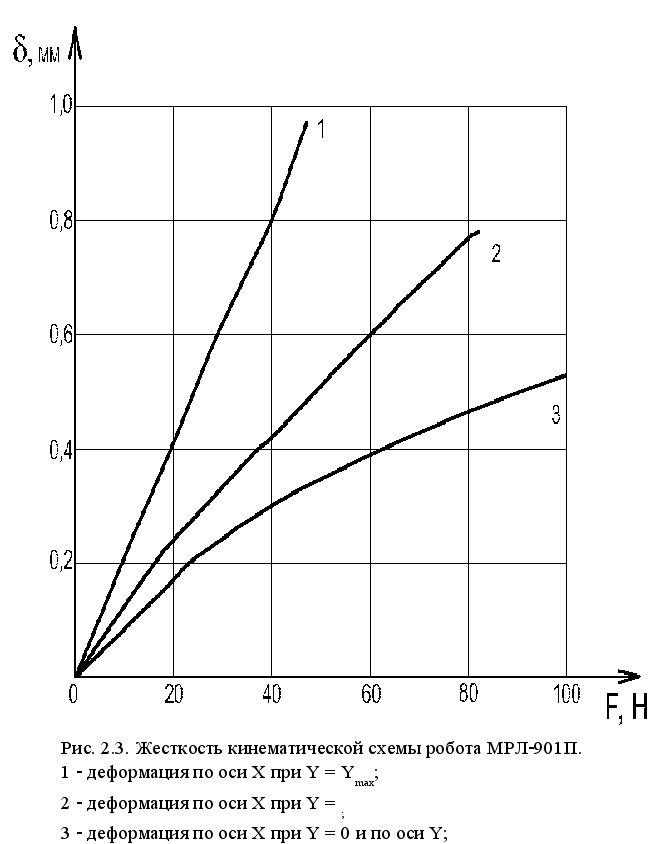
Жесткость звеньев манипулятора МРЛ-901П определялась по экспериментальным замерам деформации консоли манипулятора при действии на нее определенного усилия.
| Таблица 2.5 | ||||
| Деформация звеньев манипулятора МРЛ-901П под действием возмущающих сил | ||||
Возму- щающая сила |
Деформация звеньев манипуляционной системы d , мм | |||
| Ось X | Ось Y | |||
| Y=0 |  |
|||
| 0 | 0 | 0 | 0 | 0 |
| 10 | 0,111 | 0,135 | 0,178 | 0,111 |
| 20 | 0,206 | 0,234 | 0,390 | 0,206 |
| 30 | 0,265 | 0,334 | 0,560 | 0,265 |
| 40 | 0,302 | 0,418 | 0,750 | 0,302 |
| 50 | 0,345 | 0,507 | 0,930 | 0,348 |
| 60 | 0,390 | 0,580 | 1,090 | 0,393 |
| 70 | 0,418 | 0,658 | 0,421 | |
| 80 | 0,460 | 0,745 | 0,465 | |
| 90 | 0,498 | 0,825 | 0,505 | |
| 100 | 0,534 | 0,902 | 0,540 | |
Результаты исследования жесткости приведены в таблице 2.5. По этим данным были построены график зависимости деформации от смещения рабочего органа (рис. 2.3) и график зависимости деформации от натяжения зубчатого ремня (рис.2.4).
2.4 Исследование быстроходности манипулятора
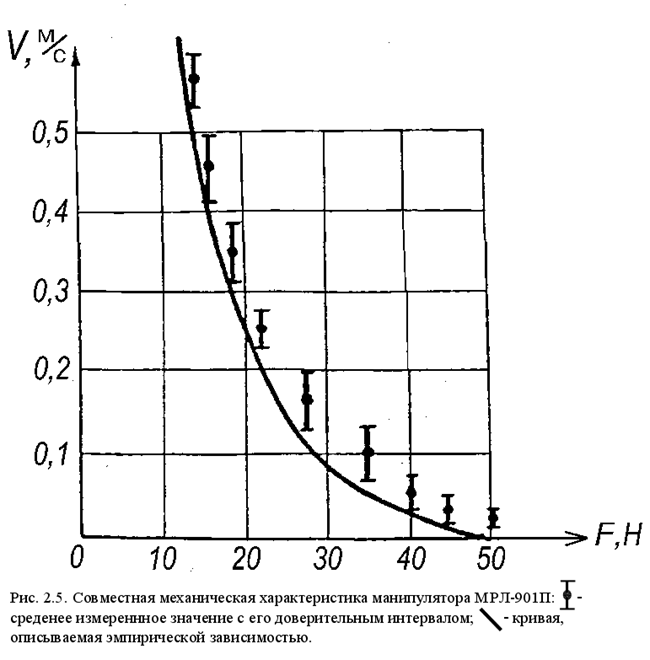
Быстроходность манипулятора характеризуется временем перемещения рабочего органа в требуемую точку. Теоретические предпосылкиуказывают, что непосредственное влияние на величину этого времени оказывают совместные механические характеристики (СМХ) электроприводов манипулятора.
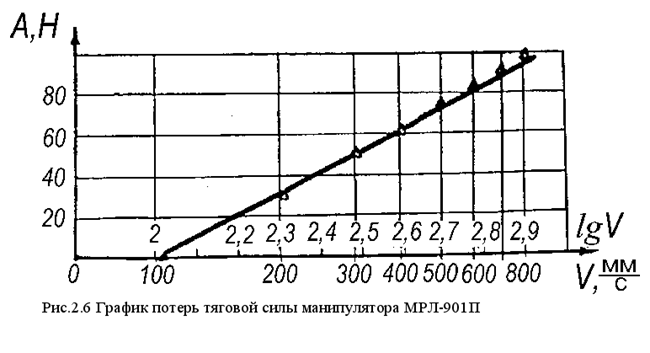
Иcследование СМХ осуществлялось путем анализа тахограмм движения манипулятора МРЛ-901П, зарегистрированных самописцемН338Д/1.Статистически обработанные результаты экспериментов сведены в таблицу 2.6 и представлены в графическом виде на рис. 2.5.
Анализ экспирементальных данных показывает, что связь силы тяги, а, следовательно, и допустимого ускорения ![]() со значением достигнутой скорости
со значением достигнутой скорости ![]() существенно нелинейна. Для определения квазиоптимальных режимов движения манипулятора необходимо связать параметры a
и V
аналитическим выражением.
существенно нелинейна. Для определения квазиоптимальных режимов движения манипулятора необходимо связать параметры a
и V
аналитическим выражением.
Представим каждое значение ![]() СМХ в виде разности
СМХ в виде разности ![]() , где
, где ![]() - статическая тяговая синхронизирующая сила, а
- статическая тяговая синхронизирующая сила, а ![]() - потери тяговой силы, зависящие от скорости движения манипулятора.
- потери тяговой силы, зависящие от скорости движения манипулятора.
Такая запись СМХ имеет то очевидное приемущество, что для каждого конкретного образца манипулятора указанной модели могут быть введены уточнения формулы путем измерения одного лишь значения ![]() .
.
Следовательно, определение эмпирической формулы CМХ сводится к отысканию зависимости ![]() . Воспользовавшись способом отыскания эмпирических формул, приведенным в [7], легко установить, что экспериментальные точки
. Воспользовавшись способом отыскания эмпирических формул, приведенным в [7], легко установить, что экспериментальные точки ![]() наиболее точно отображают линейную зависиюсть на полулогарифмической функцональной координатной сетке. Из этого следует, что выражение
наиболее точно отображают линейную зависиюсть на полулогарифмической функцональной координатной сетке. Из этого следует, что выражение ![]() может быть описано логарифмической функцией. Из
может быть описано логарифмической функцией. Из
Результаты исследований совместной механической характеристики манипулятора МРЛ-901П.
| Таблица 2.6 | ||||
Масса |
Число |
Численное значение синхронной скорости, м/c |
||
| груза |
паралельных опытов | среднее арифметическое |
среднее квадратическое откланение | принимаемое значение |
| 2 | 10 | 0,80 | 0,013 | 0,8±0,04 |
| 3 | 10 | 0,74 | 0,017 | 0,74±0,05 |
| 4 | 10 | 0,67 | 0,016 | 0,67±0,05 |
| 5 | 10 | 0,59 | 0,007 | 0,59±0,02 |
| 6 | 10 | 0,49 | 0,013 | 0,49±0,04 |
| 7 | 10 | 0,38 | 0,012 | 0,38±0,04 |
| 8 | 10 | 0,29 | 0,010 | 0,29±0,03 |
| 9 | 10 | 0,24 | 0,013 | 0,24±0,04 |
| 10 | 10 | 0,20 | 0,011 | 0,20±0,03 |
| 11 | 10 | 0,16 | 0,013 | 0,16±0,04 |
| 12 | 10 | 0,12 | 0,006 | 0,12±0,02 |
| 13 | 10 | 0,05 | 0,003 | 0,05±0,01 |
линейной зависимости, представленной на рис. 2.6 легко отыскать коэффициенты ее уравнения, вид которого ![]() . В итоге имеем:
. В итоге имеем:
| (2.35) |
где: V
измеряется в ![]() .
.
Следует, однако, заметить, что при нарастании значения экспериментальные точки ![]() несколько удаляются от прямой, описанной уравнением (2.35). Поэтому, с целью уточнения зависимости была внесена поправка, с учетом которой эмпирическая формула СМХ примет вид:
несколько удаляются от прямой, описанной уравнением (2.35). Поэтому, с целью уточнения зависимости была внесена поправка, с учетом которой эмпирическая формула СМХ примет вид:
| (2.36) |
где: V
-
измеряется в ![]() ; а
; а ![]() - в [Н], или
- в [Н], или
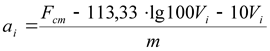 , , |
(2.37) |
где: ![]() ,
,![]() - допустимые мгновенные значения ускорения и скорости соответственно (при этом лежит в интервале от 0,1
- допустимые мгновенные значения ускорения и скорости соответственно (при этом лежит в интервале от 0,1![]() до 0,8
до 0,8 ![]() ).
).
2.5 Методика проведения эксперимента по определению механических характеристик манипулятора МРЛ-901П
Для исследования СМХ манипулятора портального типа МРЛ-901П наиболее удобной является следующая методика измерений.
Н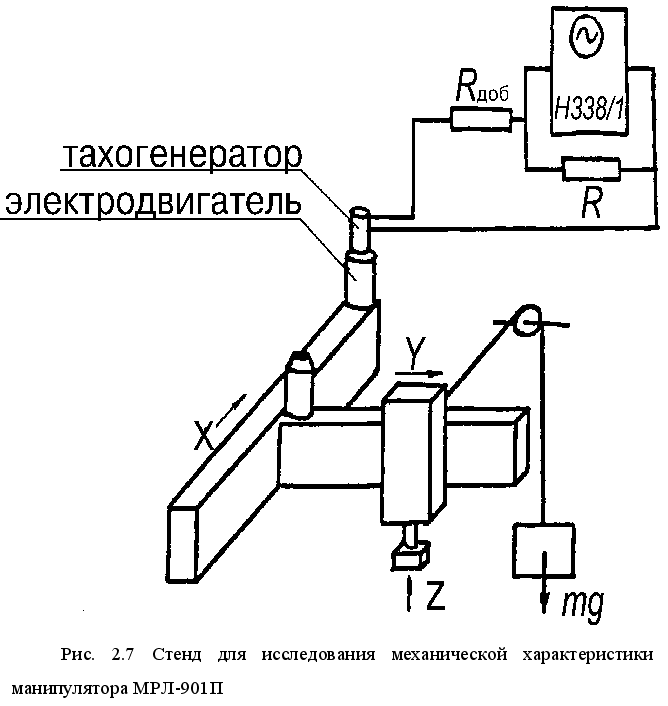
а свободный конец вала электродвигателя ШД 5Д1МУ3 крепился тахогенератор, электрический выход которого связан с
29-04-2015, 04:09
