Міністерство освіти і науки України
Волинський національний університет ім. Лесі Українки
географічний факультет
Реферат на тему:
«Оцінка точності при параметричному методі врівноваженн я »
Виконала:
Студентка 25 групи ЗІК
Витрикуш Анастасія
Володимирівна
Викладач:
Бліндер Ю. С.
Луцьк- 2010
План
Вступ.
1) Суть завдання врівноваження геодезичних побудов.
2) Основні способи врівноваження геодезичних побудов.
3) Суть і послідовність врівноваження параметричним способом.
4) Оцінка точності при парметричному методі врівноваженні.
Висновок
Список використаної літератури
Вступ
Геодезія займається вивченням Землі в геометричному відношенні. Назва геодезія походить від грецьких слів: гео-земля та дазаман-ділю, тобто Землі розділення. Звідси видно, що геодезія дуже близька до геометрії-науці про вимір. Обидві ці науки зародилися в далекій давнині. З розвитком людського суспільства геометрія стала займатися вивченням просторових форм, а практична частина в додатку до питань виміру на землі отримала назву геодезія.
Геодезія у свою чергу тісно пов'язана з картографією-наукою про складання карт. Геодезичні матеріали служать основою для складання карт. Завданням геодезії є вивчення деталей земної поверхні. У результаті вивчення отримують плани, карти та числові характеристики, що відносяться до Землі в цілому і окремих дільницях, лініях і точкам на ній. У геодезії вивчаються способи та інструменти, що застосовуються при вимірюванні кутіві довжин ліній.
Матеріали геодезичних робіт у вигляді планів, карт і числових величин (координат і висот) точок земної поверхні мають велике застосування в різних галузях народного господарства. Усяке споруда проектують з урахуванням наявних на місцевості контурів споруд, доріг, водних джерел, ґрунту. Тому для проектування необхідний план місцевості з докладним відображенням всіх деталей. Проектування та будівництво сіл, міст, залізних і шосейних доріг не можна виконувати без геодезичних матеріалів. Геодезичні роботи за змістом і характером поділяються на дві стадії: 1. польові вимірювальні роботи із застосуванням сучасної геодезичної техніки. 2. обчислювальна обробка результатів вимірювань, графічне складання та оформлення планів і карт.
Винятково велике значення планова-картографічний матеріал має в сільському господарстві. Землевпорядні органи займаються проблемою раціонального використання землі.
Перед сільським господарством стоять завдання зрошення, осушення земельних ділянок, поведінка заходів щодо боротьби з ерозією грунтів та ін всі ці питання можна вирішити тільки з використанням геодезії. Для вирішення багатьох питань необхідні плани, карти, що відображають рельєф, межі видів ґрунтів, рослинності, водойм та ін Методи вивчення Землі в цілому, як планети значно відрізняються від методів вивчення окремих ділянок поверхні. Земля є сферичне тіло, отже, досліджуючи її в цілому або великих її ділянок необхідно враховувати сферичність, що і вивчає наука вища геодезія.
Суть завдання врівноваження геодезичних побудов
Геодезичні побудови створюються для забезпечення єдиної системи координат і висот, для визначення взаємного положення точок, що знаходяться на земній поверхні, під і над нею. При цьому об'єкти можуть бути нерухомими (рівновага об'єктів) або знаходиться в русі.
Геодезичними побудовами є різні геометричні фігури, в яких вимірюються довжини ліній, кути, перевищення. Розрізняють такі геодезичні побудови:
1) ряди і мережі тріангуляції, трилатерації, лінійно-кутові мережі;
2) ходи і мережі полігонометричні, нівелірні, теодолітні, висотно теодолітні;
3) просторові геодезичні і космічні мережі і ін.
У цих мережах прямим або непрямим способом вимірюються різні елементи, які дають можливість знайти невідомі параметри (координати і висоти), що характеризують взаємне положення вершин геометричних фігур в просторі. У будь-якому геодезичній побудові вимірюються k невідомих величин, які вистачає для відшукання невідомих нам параметрів. Наприклад, в мережі тріангуляцію досить знати один базис і виміряти по два кути в кожному трикутнику (рис. 1).
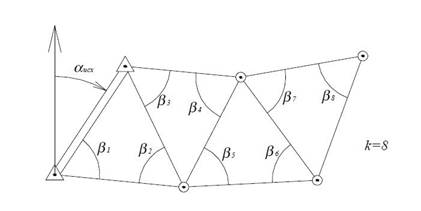
Рис.1 – Необхідні величини.
Крім того, вимірюються r надлишкових (додаткових) величин, необхідних для відбракування грубих вимірів, підвищення точності визначення шуканих параметрів і для оцінки точності вимірів і визначуваних параметрів (рис. 2). Наприклад, в приведеній раніше мережі тріангуляції необхідно виміряти додатково треті кути в трикутниках і вихідний (останній) базис і так далі.
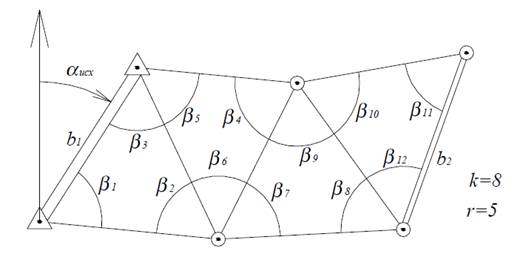
Рис. 2 Необхідні і надлишкові величини.
Надлишкові величини пов'язані з необхідними математичними співвідношеннями. Наприклад, в даній мережі тріангуляції сума кутів в кожному трикутнику повинна бути рівна 180˚. Або b1 і b2 зв'язані між собою трикутниками, вирішення яких виробляється по теоремі синусів.
Всього в кожній побудові виконується n = k + r вимірів. Слід мати на увазі, що для визначення координат кожної точки необхідно виконати по 2 виміри, а для визначення висот кожної точки – по одному виміру.
Всі виміри n = k + r елементів геодезичної побудови супроводяться похибками (випадковими і систематичними). Тому виміряні значення елементів мережі відрізняються від їх дійсних значень, а з цього виходить, що математичні співвідношення між значеннями елементів в мережі не дотримуються.
Нехай для елементів Xi отримані результати вимірів xi. Ці результати є функціями його елементів. Обчислене по виміряних елементах значення параметра y=f(x1, x2 ..., xn) відрізняється від його дійсного значення
Y=f(X1, X2 ..., Xn) і має дійсну похибку ∆y=y-Y.
Ця похибка ∆y функціонально залежить від похибок виміру елементів ∆i. До того ж кожен параметр може бути знайдений по різних комбінаціях k елементів з n виміряних. Значень одного і того ж параметра, що набувають при цьому, будуть різні.
Елементи геодезичної побудови зв'язані між собою різними геометричними умовами, які можна записати в наступному вигляді:
Ці рівняння називаються умовними рівняннями або рівняннями зв'язку. При підстановці в умовні рівняння виміряних значень елементів отримують нев'язки.
Якщо нев'язки wj не перевищують допустимого значення, то виміри вважаються виконаними правильно. У такому разі виміри зрівнюються для усунення нев'язок, визначення зрівняних значень елементів xi і оцінки їх точності. Це основні завдання зрівнювання. При підстановці зрівняних значень елементів x’i в умовні рівняння отримуємо:
Параметр геодезичної побудови, обчислений по зрівняних елементах, набуває лише одне значення
Крім того, зрівняні значення елементів володіють меншою (по абсолютній величині) похибкою, чим виміряні значення елементів, тобто
,
де 
Таким чином, врівноваження забезпечує:
1) однозначне визначення параметрів геодезичної побудови;
2) підвищення точності визначення елементів і параметрів побудови.
Зрівнювання геодезичних побудов виконується в тих випадках, коли:
1) відомі вихідні дані, яких вистачає для обчислення визначуваних параметів побудови;
2 ) виконано n вимірів, причому n>k (k – число необхідних вимірів);
3) серед виміряних n елементів побудови є k величини, необхідні і достатні для відшукання визначуваних параметрів.
Основні способи врівноваження геодезичних побудов
Основними є два способи зрівнювання:
1) параметричний спосіб (спосіб необхідних невідомих);
2) коррелатний спосіб (спосіб умов).
Окремі способи зрівнюваннями, що мають свої назви, є видозміни або різні комбінації цих способів (зрівнювання вимірів однієї величини, групове зрівнювання, параметричний спосіб з надлишковими невідомими, спосіб умов з додатковими невідомими і ін.)
Параметричний спосіб заснований на тому, що кожен елемент геодезичної побудови xi функціонально пов'язаний з системою незалежних між собою параметрів y1, y2, ..., yk, достатніх для визначення взаємного положення пунктів геодезичної побудови, тобто
де Xi і Yj – дійсні значення елементів і параметрів геодезичної побудови. При зрівнюванні параметричним способом визначають зрівняні значення параметрів y’1, y’2, ..., y’k, необхідних для представлення всіх елементів геодезичної побудови в наступному вигляді:
де xi і vi – виміряне значення i-того елементу побудови і поправка до нього. З цього рівняння отримують систему початкових рівнянь поправок або параметричні рівняння:
Для приведення цих рівнянь до лінійного вигляду знаходимо наближені значення невідомих параметрів y1, y2 ..., yk і представляємо їх зрівняні значення у вигляді:
де tj – невеликі по абсолютній величині поправки до наближених значень параметрів.
Розкладемо функцію fi(y’1, y’2, ..., y’k) в ряд Тейлора і, обмежуючись лише лінійними членами, отримаємо:
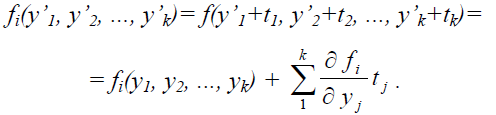
Приймемо, що
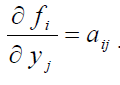
Тоді
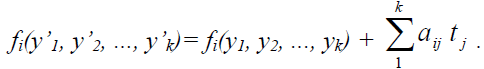
Отже,
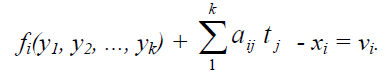
Приймемо, що
тобто li – це різниця між елементами, обчисленими по наближених параметрах і їх виміряними значеннями. Тоді отримаємо систему параметричних рівнянь поправок в лінійному вигляді
Число цих рівнянь дорівнює числу n виміряних величин, а число невідомих параметрів – k, причому k<n. Така система рівнянь є невизначеною. Вона має безліч рішень. Для здобуття однозначного рішення необхідно введення додаткових умов, при яких виробляється зрівнювання.
Зрівнювання параметричним способом полягає у відшуканні поправок t1, t2, ..., tк наближених значень шуканих параметрів у1, у2, ..., уk, їх зрівняних значень у’1 у’2 ., у’k і х’1, х’2 ., х’n, а також в оцінці точності результатів врівноваження.
Коррелатний спосіб зрівнювання полягає у вирішенні системи r незалежних умовних рівнянь, що виникають при вимірі r надлишкових елементів в геодезичній побудові.
Умовне рівняння має вигляд:
(1)
де wj – нев'язки в умовних рівняннях.
Для приведення умовних рівнянь до лінійного вигляду приймемо, що:
де xi і vi – виміряне значення i-того елементу геодезичної побудови і поправка до нього.
Поправки vi усувають нев'язку wj (умова зрівнювання). Тоді:
Поправки vi малі по абсолютній величині порівняно із значеннями елементів, тому розкладемо функцію f(x’i) в ряд Тейлора і обмежуючись лише членами першого порядку отримаємо:
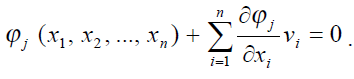
Приймемо, що
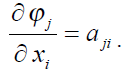
Тоді
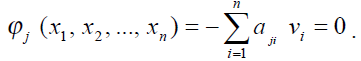
Підставивши отримане рівняння у формулу 1 отримаємо систему умовних рівнянь поправок в лінійному вигляді:
Дана система r рівнянь з n невідомими є невизначена, оскільки r<n. Тобто система умовних рівнянь поправок має безліч рішень і для її вирішення необхідно ввести додаткові умови.
Параметричний спосіб зрівнювання і спосіб умов є еквівалентними за однакових додаткових умов, тобто приводять до однакових значень зрівняних елементів геодезичної побудови.
Суть і послідовність врівноваження параметричним способом
При побудові геодезичних мереж на місцевості закріплюються пункти, координати і висоти яких є шуканими величинами. Як правило, при зрівнюванні геодезичних мереж параметричним способом шукані параметри приймаються:
1) координати X і Y пунктів при зрівнюванні планових мереж;
2) висоти Н пунктів при врівноваженні висотних мереж.
Елементами геодезичних мереж є вимірювані на місцевості горизонтальні кути, довжини ліній, перевищення між точками, введемо наступні позначення (k<n):
1) Yj (j = 1, k) – дійсні значення шуканих параметрів або необхідних невідомих;
2) y* j (j = 1, k) – зрівняні значення параметрів;
3) yj (j = 1, k) – наближені значення параметрів;
4) tj (j = 1, k) – поправки в наближені значення параметрів;
5) Xi (i = 1, n) – дійсні значення елементів мережі;
6) x*i (i = 1, n) – зрівняні значення елементів;
7) vi (i = 1, n) – поправки у виміряні значення елементів мережі;
8) aij (i = 1, n; j = 1, k) – коефіцієнти параметричних рівнянь поправок;
9) li (i = 1, n) – вільні члени параметричних рівнянь поправок;
10) Pi (i = 1, n) – ваги результатів вимірів.
При врівноваженні параметричним способом складається система параметричних рівнянь поправок
де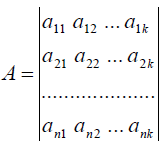 
- матриця коефіцієнтів параметричних рівнянь поправок розміром k*n;
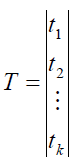- вектор поправок до вектора наближених значень параметрів yj;
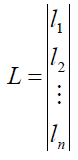- вектор вільних членів системи параметричних рівнянь поправок l= f(y1, y2 ., yk) – xi;
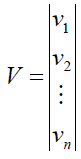- вектор поправок до вектора виміряних елементів мережі xi.
Вирішення системи параметричних рівнянь поправок полягає у відшуканні вектора поправок Т до наближених значень параметрів
yj (j = 1, k) за умови 
де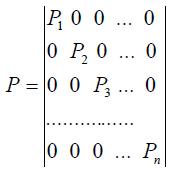 
- вагова матриця або матриця вагів результатів вимірів розміром n*n.
Для відшукання min функції необхідно прирівняти до нуля її першу похідну і вирішити отримані рівняння. У нашому випадку:
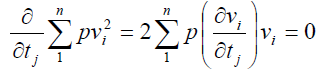
З системи параметричних рівнянь поправок виходить, що
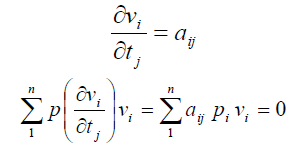
Покажемо, що умова
Рівносильно умові
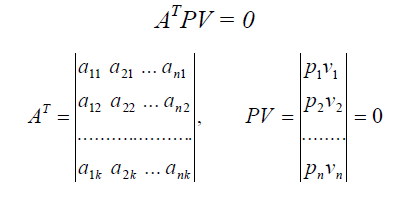
Отже:
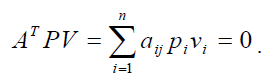
Помножимо рівняння AT + L = V зліва на 
і отримаємо:
або враховуючи умову 
Отримана система k рівнянь з k невідомими параметрами tj називається системою нормальних рівнянь. Матриця коефіцієнтів системи нормальних рівнянь має вигляд:
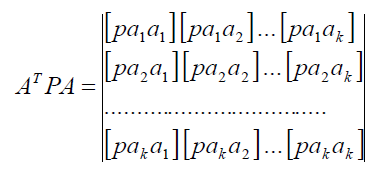
Отримана матриця:
1) квадратна матриця порядку k;
2) симетрична матриця;
3) позитивно визначена рангу k;
4) неособлива.
В результаті вирішення системи нормальних рівнянь отримуємо поправки tj до наближених значень параметрів yj, а потім по формулі
y*j = yj + tj зрівняні значення параметрів. Поправки vi до виміряних значень елементів мережі xi обчислюються за формулою:
Потім обчислюються зрівняні значення елементів мережі:
Контроль вирішення системи нормальних рівнянь обчислення поправок vi і зрівняних значень x*i і y*j виробляється по формулі:
тобто по зрівняних значеннях параметрів ще раз обчислюють зрівняні значення елементів мережі.
Недотримання цієї контрольної рівності може відбуватися із-за помилок в обчисленнях або унаслідок недостатньої точності наближених значень параметрів yj. У першому випадку необхідно відшукати і виправити помилки в обчисленнях. У другому випадку зрівняних значень y*j слід набути як наближені значення і з ними повторити весь процес зрівнювання.
Ознакою недостатньої точності наближених значень параметрів є недопустимо великі значення поправок tj. У цих випадках не можна нехтувати нелінійними членами розкладання функції в ряд Тейлора при обчисленні коефіцієнтів параметричних рівнянь поправок.
Оцінка точності при параметричному методі врівноваження.
Визначення середньої квадратичної погрішності одиниці ваги. Визначається по формулі:
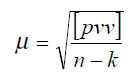
де n – число виміряних величин;
k – число необхідних вимірів.
Середня квадратична похибкам визначення m обчислюється за формулою:
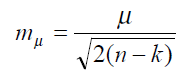
Величина [pvv] або 
може бути знайдена різними шляхами:
1) по алгоритму Гауса – при вирішенні системи нормальних рівнянь до основної системи NT + L = 0 додається ще одне рівняння
2) Знов отримана система k+1 рівнянь з k+1 невідомими зберігає всі властивості нормальних рівнянь, причому останній діагональний елемент 
Тому після виключення всіх невідомих ti отримаємо:
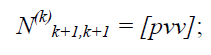
2) по обчислених поправках v – обчисливши поправки V = AT + L, де А – матриця коефіцієнтів рівнянь поправок. Обчислимо величину [pvv] за формулою:
3) по значеннях вільних членів l в рівняннях поправок і поправках v – знаючи поправки v в результати вимірів і вільні члени l рівнянь поправок знайдемо [pvv] по формулі:
або
Обчислення середніх квадратичних похибок зрівняних значень параметрів.
Виразимо невідомі Т у вигляді лінійних функцій вільних членів нормальних рівнянь
29-04-2015, 00:30