Типові записи навантажень у верхній частині бурильної колони при гальмуванні в процесі спуску. Поява періодичних піків зусиль пояснюється періодичним вмиканням гальма бурової лебідки.
Проведений початковий аналіз записів експлуатаційного навантажування під час спуску свідчить про значний розкид значень асиметрії циклів. Для довжини 190 м і, особливо, 500 м характерною особливістю є значний вплив високочастотної складової з низькими амплітудами. При довжині 1580 м спостерігається значне збільшення кількості високоамплітудних напружень. Високочастотні напруження, характерні для менших довжин, майже не спостерігаються. Це пояснюється тим, що при довжині БК 1580 м використовувалось гідравлічне гальмо, яке значно зменшує високочастотні коливання.
У розділі також представлено результати експериментальних досліджень навантаженості колони насосних штанг. Дослідження проводились на свердловинах № 4, 88 та 90 Довбушансько-Бистрицького нафтового родовища, оснащених штанговими свердловинними насосними установками. На свердловинах записувались динамограми за допомогою гідравлічного динамографа ГДМ-3 та розробленої вимірювальної системи з використанням індуктивного давача малих переміщень. При цьому проводився запис діючих зусиль протягом певного часу, що давало можливість оцінити сталість процесу навантаження. Приклади запису наведено на рис. 2.
Як відомо, свердловини України характеризуються значною викривленістю. У такому випадку в процесі роботи, крім змінних напружень розтягу, БК і КНШ підлягають впливу додаткових циклічних локальних напружень згину на викривлених ділянках. Тому однією із задач досліджень є визначення напружень у БК і КНШ на викривленій ділянці з урахуванням поздовжніх сил розтягу.
З використанням розробленої методики чисельного розв’язку проведено оцінку впливу геометрії викривленої ділянки свердловини на напруження згину КНШ з урахуванням поздовжньої сили розтягу. Деякі результати розв’язку наведено на рис. 3.
Слід звернути увагу на значний вплив напружень розтягу на амплітуду циклічних напружень згину, а отже, і на довговічність колони штанг на викривленій ділянці. Так, якщо напруження розтягу внизу колони будуть змінюватися від 0 до 1,8 МПа при силі розтягу 500 Н, то напруження згину на ділянці з кутом викривлення 20º і радіусом 50 м – від 50,7 до 207,3 МПа. Таким чином, амплітуда згинаючих напружень досягає 78,3 МПа, що може служити основною причиною втомного руйнування колони у нижній частині на викривлених ділянках.
Проведено аналітичні дослідження з визначення сил та напружень в БК на викривленій ділянці з урахуванням розтягу і зазору між БК та стінкою свердловини. Розроблено критерій вибору положення бурильної колони на викривленій ділянці свердловини. Показано, що нехтування силами розтягу та неспівпадінням осі свердловини і бурильної колони може призвести до похибок при розрахунках напружено-деформованого стану та довговічності бурильних труб. Так, наприклад, визначено напруження у поперечному перерізі бурильних труб ТБПК 127 (товщина стінки 8 мм) у криволінійному стовбурі свердловини діаметром 295,3 мм. При відстані від нейтрального перерізу до початку криволінійної ділянки ![]() =250 м колона буде доторкатися до нижньої частини стінки свердловини по всій довжині. У цьому випадку напруження згину – 9,5 МПа. При збільшенні
=250 м колона буде доторкатися до нижньої частини стінки свердловини по всій довжині. У цьому випадку напруження згину – 9,5 МПа. При збільшенні ![]() до 260 м, сила розтягу зростає і стає достатньою для відриву колони від стінки свердловини. Напруження зростає до 11,9 МПа. При наступному збільшенні
до 260 м, сила розтягу зростає і стає достатньою для відриву колони від стінки свердловини. Напруження зростає до 11,9 МПа. При наступному збільшенні ![]() (понад 260 м), сила розтягу спричиняє контакт бурильної колони із верхньою частиною стовбура свердловини, а величина напружень збільшується від 15,2 до 40,2 МПа при збільшенні
(понад 260 м), сила розтягу спричиняє контакт бурильної колони із верхньою частиною стовбура свердловини, а величина напружень збільшується від 15,2 до 40,2 МПа при збільшенні ![]() до 300 м.
до 300 м.
У розділі також проведено аналіз процесу СПО при каротажних роботах під час спорудження свердловин. Даний процес характеризується високим ступенем непрогнозованості через неможливість попереднього урахування усіх вагомих чинників, особливо сили контактного тертя пристрою і кабелю об глинисту кірку та інерційних сил. Тому експериментальне визначення натягу кабелю в експлуатаційних умовах має велике теоретичне і практичне значення як для оптимізації процесу СПО при каротажних роботах, так і для прогнозування довговічності та залишкового ресурсу кабелю.
Проведено серію експериментальних досліджень натягу кабелю при СПО в експлуатаційних умовах при різних швидкостях піднімання найбільш поширених каротажних пристроїв на глибинах 100-5000 м для свердловин з характерними профілями.
Результати отримано за допомогою установки КТРС-10М. Характерні графіки зміни сили натягу кабелю наведено на рис. 4.
Аналіз результатів дає підстави зробити висновок про лінійну залежність сили натягу від глибини знаходження каротажного пристрою. Увагу привертає значний вплив прихоплень пристрою, які не тільки призводять до значних однократних перевантажень (рис. 4а), але й для похило-спрямованих свердловин можуть суттєво збільшити силу опору руху пристрою (див. рис. 4б, в), а також призвести до значних циклічних коливань і, як наслідок, до інтенсифікації втомного пошкодження кабелю (див. рис. 4г).
Розділити сили контактного та рідинного опору загалом досить важко через їх складну природу. Тому було проведено експериментальні дослідження натягу кабелю при підніманні в вертикальній свердловині, для якої впливом сил контактного опору можна знехтувати.
Аналіз одержаних результатів дав можливість розрахувати сили гідравлічного опору для різних швидкостей виконання спуско-піднімальних операцій і різних каротажних приладів. Результати розрахунків наведено на рис. 5.
Увагу привертає позитивний вплив збільшення швидкості на зменшення сили опору руху каротажних пристроїв і екстремальний характер сили опору геофізичного кабелю за швидкості u=500 м/год. За допомогою отриманих результатів можна більш упевнено керувати процесом проведення каротажних операцій як з точки зору продуктивності, так і уникнення аварійних ситуацій. Також з їх допомогою можна провести аналіз закономірностей зміни контактних сил опору з урахуванням швидкості і зенітного кута свердловини, що є необхідним при прогнозуванні СПО під час проведення каротажних операцій та максимальної глибини опускання каротажного пристрою для свердловин зі складним профілем.
У четвертому розділі наведено результати дослідження закономірностей накопичення втомного і корозійно-втомного пошкодження в умовах широкосмугового процесу навантажування.
Слід зауважити, що при складному випадковому процесі навантажування спостерігаються найбільші розбіжності між теоретичними розрахунками довговічності та залишкового ресурсу і експериментальними результатами. У першу чергу, це пов’язано з недостатнім урахуванням дії двох чинників. По-перше, це вплив послідовності амплітуд циклів напружень. У багатьох випадках таким впливом не можна нехтувати, наприклад, у випадку наявності в блоці навантажування високих, так званих пікових напружень, або низьких напружень, менших за границю витривалості. По-друге, значення відносного накопичення пошкоджень залежить від коефіцієнту широкосмуговості e, а саме, його зменшення, тобто збільшення широкосмуговості і складності процесу навантажування, призводить до значного зменшення точності оцінки довговічності за існуючими методами підсумовування пошкоджень. Таким чином, необхідною передумовою створення універсального методу підсумовування втомних пошкоджень при складному широкосмуговому навантажуванні є одночасне врахування впливу як послідовності амплітуд циклів напружень, так і багаточастотності процесу навантажування. На нашу думку, на сучасному етапі оцінити комплексний вплив даних чинників можливо тільки на основі їх окремого враховування.
Тому для врахування складності процесу навантажування РЕСО запропоновано метод, який ґрунтується на роздільному враховуванні багаточастотності процесу і його складності на окремих частотах з допомогою окремих коефіцієнтів.
Сумарне пошкодження визначаємо за запропонованою формулою
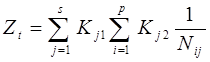 , (1)
, (1)
де s – кількість етапів схематизації;
p – кількість циклів напружень на етапі схематизації;
![]() – кількість циклів напружень до руйнування при дії циклу напружень
– кількість циклів напружень до руйнування при дії циклу напружень ![]() ;
;
Кj1 – коефіцієнт, який враховує вплив напружень попереднього рівня на напруження даного (К11 =1);
Кj2 – коефіцієнт, який враховує нерівномірність амплітуд у часі всередині рівня.
Якщо прийняти в першому наближенні всі Кj =1, то дане рівняння буде відповідати рівнянню Майнера. Тому основну увагу слід приділити визначенню Кj . Суть пропонованих коефіцієнтів полягає у виділенні найбільш суттєвих ознак реального процесу широкосмугового навантажування. Згідно з розробленим методом схематизації напружень реальний процес навантажування моделюється циклами еквівалентних напружень, приведеними до окремих рівнів з різною частотою.
Визначення К21 , К31 і т.д. можна провести згідно з аналізу двочастотних процесів, де накопичено вже значну кількість інформації. У загальному випадку для визначеного матеріалу
Кj1
=F(![]() ,
,![]() ).
).
Визначення коефіцієнта Кj значно полегшується при наявності інформації про матеріал, а саме про його реакцію на зміну напружень. Доцільно поділити усі матеріали за такими ознаками:
1. Матеріал не реагує на зміну напружень в процесі навантажування і для нього усі Кj =1, тобто формула Майнера справедлива в усіх випадках.
2. Матеріал реагує на зміну напружень, але загальна реакція на зміну ![]() на
на ![]() і навпаки зрівноважується. Для такого випадку
і навпаки зрівноважується. Для такого випадку ![]() , а Кj1
¹1 при
, а Кj1
¹1 при ![]() .
.
3. Матеріал реагує на зміну навантаження. Тоді Кj1
¹1, а Кj2
=F(![]() D
D![]() ) ¹1 і його вплив тим більший, чим більше значення
) ¹1 і його вплив тим більший, чим більше значення ![]() , тобто варіація процесу.
, тобто варіація процесу.
Проведений аналіз свідчить, що для РЕСО характерними процесами навантажування є широкосмугові процеси зі значними амплітудами циклів тільки на найнижчій частоті. Для такого випадку досить обмежитись аналізом послідовності тільки низькочастотних амплітуд та впливом на їх пошкоджуючу дію високочастотної складової.
Для реалізації розробленого методу підсумовування пошкоджень складним є вже перший етап, на якому проводиться схематизація випадкових навантажувань з приведенням їх до еквівалентних за пошкоджуючою дією закономірних чи блокових. На сучасному етапі поки що немає загальноприйнятої методики вирішення цієї задачі. Існуючі методи схематизації (екстремумів, розмахів, викидів, повних циклів, “дощу” тощо) дають різні розподіли навантажень.
Традиційними методами схематизації неможливо враховувати водночас історію навантажування та складність самого процесу через їх орієнтацію на розподіл величин амплітуд без визначення їх послідовності (метод повних циклів, “дощу”) чи без врахування складності процесу (метод розмахів, метод екстремумів, метод викидів).
Значною мірою поставленій меті відповідає метод, запропонований Є.К.Почтєнним спершу для двочастотного процесу, а пізніше розвинутий для багаточастотного навантажування. Поетапне виділення максимумів процесу, запропоноване в даному методі, дає можливість провести аналіз процесу як з точки зору послідовності амплітуд, так і складності структури, яка враховується кількістю виділених етапів схематизації. Так, двочастотний процес описується в 2 етапи, тричастотний – в 3 і т.д. Варто зауважити, що кількість етапів не залежить від того, чи однакові амплітуди на якійсь частоті, чи випадкові, та й від випадковості розподілу самих частот процесу. Кожний наступний етап є більш низькочастотним за попередній (мінімум у 2 рази). Крім цього, з допомогою одержаної інформації також можна зробити приблизний частотний аналіз процесу. Але запропоноване в даному методі поетапне виділення максимумів процесу не дає можливості в достатній мірі дослідити структуру процесу, особливо у випадку складного багаточастотного навантажування з випадковими істотно різними амплітудами. При врахуванні тільки максимумів такого процесу існує можливість спотворення реальної картини процесу, особливо завищення середнього напруження циклу ![]() на найбільш низьких виділених частотах.
на найбільш низьких виділених частотах.
Найбільш істотно реальний процес навантажування відрізняється від схематизованого у двох випадках.
1. ![]() (2)
(2)
У цьому випадку схематизація за даним методом призводить до заниження реальної складності процесу. Врахування тільки максимумів такого процесу не дає можливості оцінити його низькочастотні складові, які можуть суттєво впливати на довговічність деталей при такому характері випадкового навантажування.
2. ![]() (3)
(3)
У даному випадку ситуація є протилежною і схематизація за методом Є.К.Почтєнного свідчить про високу складність структури випадкового процесу. Але такий процес характеризується складністю розподілу послідовності амплітуд, а не самої структури. Тому такий випадковий процес повинен описуватися одноетапною схематизацією, а вже сама складність розподілу амплітуд в часі повинна враховуватися під час аналізу схематизованого процесу. Виокремлення ж при схематизації такого процесу великої кількості низькочастотних складових тільки ускладнює даний аналіз.
Тому для одночасного враховування впливу як послідовності амплітуд циклів напружень, так і багаточастотності процесу навантажування, розроблено метод схематизації шляхом поетапного виділення середніх значень амплітуд, названий методом вкладених циклів.
Суть методу полягає в наступному. Початковим етапом схематизації є, як і для інших методів, визначення екстремумів процесу ![]() . Потім, як і для методу Є.К.Почтєнного, для кожного із сусідніх півциклів визначається амплітуда
. Потім, як і для методу Є.К.Почтєнного, для кожного із сусідніх півциклів визначається амплітуда ![]() та середнє значення
та середнє значення ![]() . Це дає можливість визначити послідовність амплітуд на першій найбільш високій частоті процесу.
. Це дає можливість визначити послідовність амплітуд на першій найбільш високій частоті процесу.
На другому етапі розглядається процес, при якому до уваги беруться обчислені раніше середні значення ![]() .
.
Для цього процесу визначаються екстремальні значення, а інші точки процесу з подальшого розгляду відкидають.
Знову визначаються, як і для першого етапу, ![]() і
і ![]() . Таким чином, ми отримуємо розподіл амплітуд та їх послідовність на другій, більш низькій частоті.
. Таким чином, ми отримуємо розподіл амплітуд та їх послідовність на другій, більш низькій частоті.
Таку процедуру повторюють до того часу, поки на якомусь етапі різниця між максимальним і мінімальним значенням процесу не стане меншою за якесь заздалегідь визначене значення [![]() ], наприклад,
], наприклад, ![]() ; або не залишаться 2-3 екстремальні точки.
; або не залишаться 2-3 екстремальні точки.
Використання методу вкладених циклів відображено на прикладі випадкового процесу, для якого проведено аналіз згідно з методами “дощу”, повних циклів та врахування одного екстремуму між сусідніми перетинами середнього рівня. Проведений аналіз свідчить про досить близьку відповідність розподілів, проведених згідно з пропонованим методом і методом “дощу”, який на сьогоднішній день вважається найбільш прийнятним при розрахунках. Але головною перевагою запропонованого методу вкладених циклів є одержання розподілу в часі амплітуд напружень при одночасному визначенні реальної складності структури процесу. Це дає можливість більш повно враховувати історію навантажування та складність структури процесу при розрахунках на довговічність.
Процеси навантажування РЕСО характеризуються також великою асиметрією циклів напруження. У такому випадку при використанні рівняння (1) ми зіткнемося з проблемою оцінки їх пошкоджуючої дії. У зв’язку з тим, що переважну більшість експериментів з визначення параметрів опору втомі проводять при симетричному циклі напружень, необхідним етапом є приведення асиметричних циклів до еквівалентних за пошкоджуючою дією симетричних.
Для розрахункового приведення асиметричних напружень з коефіцієнтом асиметрії ![]() до симетричних пропонується, виходячи із закономірностей кінетики втомного пошкодження та лінійної залежності характеристики кута нахилу кривої втоми від асиметрії навантаження, використовувати отримане наступне рівняння
до симетричних пропонується, виходячи із закономірностей кінетики втомного пошкодження та лінійної залежності характеристики кута нахилу кривої втоми від асиметрії навантаження, використовувати отримане наступне рівняння
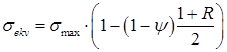 , (4)
, (4)
де ![]() – максимальне напруження симетричного циклу, яке еквівалентне за пошкодженням асиметричному з максимальним напруженням
– максимальне напруження симетричного циклу, яке еквівалентне за пошкодженням асиметричному з максимальним напруженням ![]() і коефіцієнтом асиметрії R;
і коефіцієнтом асиметрії R;
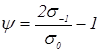 – коефіцієнт чутливості до асиметрії навантаження;
– коефіцієнт чутливості до асиметрії навантаження;
![]() – границі витривалості при симетричному і віднульовому циклах напружень відповідно.
– границі витривалості при симетричному і віднульовому циклах напружень відповідно.
Аналіз великої кількості експериментів з визначення параметрів опору втомі дає змогу стверджувати, що кут нахилу кривих з рівним ступенем пошкодження в області багатоциклової втоми задовільно описується коефіцієнтом ![]() тільки при
тільки при ![]() , а при
, а при ![]() кут нахилу збільшується при зменшенні N. Тому для більшої достовірності приведення асиметричних циклів пропонується криві рівної пошкоджуваності апроксимувати двома прямими. Для напружень з
кут нахилу збільшується при зменшенні N. Тому для більшої достовірності приведення асиметричних циклів пропонується криві рівної пошкоджуваності апроксимувати двома прямими. Для напружень з ![]() буде справедливим приведення згідно з (4). Для приведення ж циклів напружень з
буде справедливим приведення згідно з (4). Для приведення ж циклів напружень з ![]() скористаємось особливістю діаграми Хея, а саме тим, що всі криві з рівним ступенем пошкодження сходяться в точці (1,0). Схему приведення до симетричного циклу зображено на рис. 6.
скористаємось особливістю діаграми Хея, а саме тим, що всі криві з рівним ступенем пошкодження сходяться в точці (1,0). Схему приведення до симетричного циклу зображено на рис. 6.
До симетричного циклу приводимо напруження, показане на рис. 6 точкою А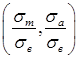 . Для цього проводимо промінь, який виходить з точки К(1, 0), через А до перетину з прямою R=0 (точка В). За аналогією з
. Для цього проводимо промінь, який виходить з точки К(1, 0), через А до перетину з прямою R=0 (точка В). За аналогією з ![]() приймемо
приймемо
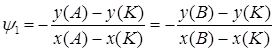 . (5)
. (5)
Тоді, враховуючи координати точок А і К, отримуємо рівняння
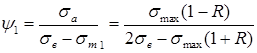 ; (6)
; (6)
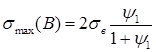 ; (7)
; (7)
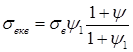 . (8)
. (8)
Для оцінки достовірності запропонованого приведення було проаналізовано результати експериментального дослідження зразків, виготовлених зі сталі 40ХН. Отримано такі параметри кривих втоми за рівнянням Є.К.Почтєнного у вигляді
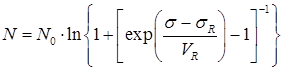 : (9)
: (9)
На рис. 7 наведено криві втоми 1, 2, побудовані згідно з даними параметрами за рівнянням (9), криву 3, побудовану за рівнянням І.А.Одінга, а також криві 4, 5 отримані шляхом приведення за допомогою рівнянь (4) і (8) відповідно. Як бачимо, в даному випадку запропонований метод приведення, на відміну від загальноприйнятого методу І.А.Одінга, практично повністю відповідає результатам експерименту. Отже, за аналізу випадкового процесу навантажування приведення до еквівалентного симетричного процесу рекомендується проводити за допомогою рівнянь
29-04-2015, 00:36
