Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Санкт-Петербургский государственный
инженерно-экономический университет»
Кафедра логистики и организации перевозок
Курсовая работа по дисциплине
транспортировка в логистике
Выполнил Маскаев Евгений Сергеевич _
(Фамилия И.О.)
студент 3 курса специальность Логистика и управление цепями поставок _
группа 2262 № зачетной книжки__________22023/06 ____________
Подпись __________________________________________________
Преподаватель Ксенофонтова Е.М. _
(Фамилия И.О.)
Должность доцент _
уч. степень, уч. Звание
Оценка_______________Дата ________________________________
Подпись__________________________________________________
Санкт-Петербург
2009
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ…………………………………………………………………………………..2
1. Нанести на оси координат OXY расположение пунктов транспортной сети………………………………………………………………………….3
2. Определить расстояния между пунктами транспортной сети…………..5
3. Решить задачи методом Фогеля, определение общего пробега, пробега с грузом и транспортную работу для маятниковых маршрутов………...6
4. Составление маршрутов движения транспортных средств методом Свира и «ветвей и границ»………………………………………………...8
5. Оценка интервалов времени прибытия и отправления транспортных средств для каждого пункта маршрутов………………………………...18
6. Выбор транспортных средств и определение затрат на транспортировку…………………………………………………………..31
7. Общие выводы…………………………………………………………….32
ВВЕДЕНИЕ
Целью выполнения курсовой работы является закрепление знаний, полученных при изучении дисциплины, и приобретение навыков решения задач по формированию маршрутов доставки груза при внутригородских перевозках на основе принципов «точно во время» и «от двери до двери», а так же в оценке времени доставки груза на основании статистических закономерностей и расчете основной статьи себестоимости – затрат на топливо.
Курсовая работа заключается в решение задач транспортной логистики с использованием экономико-математических методов на основе заданной мощности грузоотправителей и потребности грузополучателей.
1. Нанести на оси координат OXY расположение пунктов транспортной сети
Таблица 1 «Координаты пунктов погрузки, км»
| Х | У | |
| А | 13 | 12 |
| Б | 14 | 16 |
Таблица 2 «Координаты пунктов разгрузки, км»
| Х | У | |
| 1 | 7 | 13 |
| 2 | 4 | 14 |
| 3 | 5 | 18 |
| 4 | 1 | 10 |
| 5 | 12 | 7 |
| 6 | 11 | 20 |
| 7 | 10 | 8 |
| 8 | 14 | 3 |
| 9 | 10 | 3 |
| 10 | 1 | 8 |
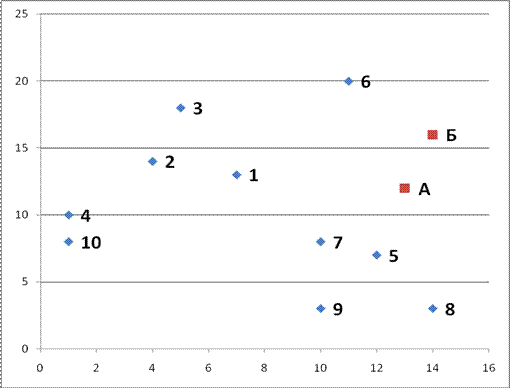
2. Определить расстояния между пунктами транспортной сети
Расстояние между двумя пунктами определяется по формуле, округляя получаемое значение до целого:
r 2 = (xi – xj )2 + (yi – yj )2
Пример:
А-1=√(13-7)2 +(12-13)2 =6
Аналогичным образом рассчитываем все остальные расстояния между пунктами загрузки и разгрузки, а также расстояния только между пунктами разгрузки.
Таблица 3 «Расстояния между пунктами погрузки и разгрузки»
| А | Б | |
| 1 | 6 | 7 |
| 2 | 9 | 10 |
| 3 | 10 | 9 |
| 4 | 12 | 14 |
| 5 | 5 | 8 |
| 6 | 9 | 6 |
| 7 | 5 | 9 |
| 8 | 9 | 12 |
| 9 | 9 | 13 |
| 10 | 13 | 15 |
Таблица 4 «Расстояния между пунктами разгрузки»
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 0 | 3 | 6 | 7 | - | 7 | 6 | - | - | 8 |
| 2 | 3 | 0 | - | 5 | - | - | 8 | - | - | 7 |
| 3 | - | - | 0 | - | - | 5 | - | - | - | - |
| 4 | 7 | 5 | - | 0 | - | - | 9 | - | - | 2 |
| 5 | - | - | - | - | 0 | - | - | 4 | 4 | - |
| 6 | 7 | - | 5 | - | - | 0 | - | - | - | - |
| 7 | 6 | 8 | - | 9 | - | - | 0 | - | - | 9 |
| 8 | - | - | - | - | 4 | - | - | 0 | 4 | - |
| 9 | - | - | - | - | 4 | - | - | 4 | 0 | - |
| 10 | 8 | 7 | - | 2 | - | - | 9 | - | - | 0 |
3. Решить задачи методом Фогеля, определение общего пробега, пробега с грузом и транспортную работу для маятниковых маршрутов
Таблица 5 «Расстояния между пунктами транспортной сети»
| Пункт погрузки | Пункт разгрузки | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| А | 6 | 9 | 10 | 12 | 5 | 9 | 5 | 9 | 9 | 13 |
| Б | 7 | 10 | 9 | 14 | 8 | 6 | 9 | 12 | 13 | 15 |
Дополним предыдущую таблицу строкой и столбцом разности.
Таблица 6 «Исходная матрица для метода Фогеля»
| Пункт погрузки | Расстояние до пункта разгрузки, км | Столбец разности | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| А | 6 | 9 | 10 | 12 | 5 | 9 | 5 | 9 | 9 | 13 | 0 |
| Б | 7 | 10 | 9 | 14 | 8 | 6 | 9 | 12 | 13 | 15 | 1 |
| Строка разностей | 1 | 1 | 1 | 2 | 3 | 3 | 4 | 3 | 4 | 2 | |
Наибольшая разность получается в столбце №9 и наименьшее расстояние в нём равно 9. Исходя из этого, закрепляем девятый пункт разгрузки за пунктом погрузки А и удаляем столбец №9 из таблицы. Затем заново рассчитываем разности и далее по аналогии закрепляем каждый столбец за пунктом погрузки.
Таблица 7 «Оптимальное закрепление пунктов разгрузки за поставщиками»
Пункт погрузки |
Расстояние до пункта разгрузки, км | Ит ого | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| А | 6 | 9 | 12 | 5 | 5 | 9 | 9 | 13 | 23,5 | ||
| Б | 9 | 6 | 6,03 | ||||||||
| Объем груза, т | 4,24 | 2,30 | 4,40 | 0,74 | 4,79 | 1,63 | 3,82 | 1,63 | 4,52 | 1,46 | 29,53 |
Теперь определим общий пробег, пробег с грузом и транспортную работу:
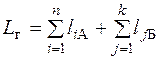 =(6+9+6+12+5+6+5+9+9+13)=83 км
=(6+9+6+12+5+6+5+9+9+13)=83 км
![]() = =2*83=166 км
= =2*83=166 км
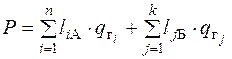 =6*4,24+9*2,30+9*4,40+12*0,74+5*4,79+6*1,63++5*3,82+9*1,63+9*4,52+13*1,46=221,78 ткм
=6*4,24+9*2,30+9*4,40+12*0,74+5*4,79+6*1,63++5*3,82+9*1,63+9*4,52+13*1,46=221,78 ткм
4. Составление маршрутов движения транспортных средств методом Свира и «ветвей и границ»
Метод Свира позволяет оптимизировать доставку грузов. Основа этого метода состоит в том, что в одно транспортное средство загружается определенный объем груза и затем последовательно выгружается в пунктах разгрузки. В качестве транспортного средства будет выбран грузовой автомобиль Mercedez-Benz 2544 с грузоподъемностью в 20 т.
Маршрут А1.
Таблица 8 «Матрица кратчайших расстояний для маршрута от грузоотправителя А1»
| Пункты маршрута | А | 5 | 8 | 9 |
| А | 5 | 9 | 9 | |
| 5 | 5 | 4 | 4 | |
| 8 | 9 | 4 | 4 | |
| 9 | 9 | 4 | 4 |
Таблица 9 «Матрица кратчайших расстояний, приведенная по строкам»
| Пункты маршрута | А | 5 | 8 | 9 | hi | |
| А | 0 | 4 | 4 | 5 | ||
| 5 | 1 | 0 | 0 | 4 | ||
| 8 | 5 | 0 | 0 | 4 | ||
| 9 | 5 | 0 | 0 | 4 | ||
| Итого: | 17 | |||||
Таблица 10 «Матрица кратчайших расстояний, приведенная по столбцам»
| Пункты маршрута | А | 5 | 8 | 9 | Итого: |
|
| А | ∞ | 0 | 4 | 4 | ||
| 5 | 0 | ∞ | 0 | 0 | ||
| 8 | 4 | 0 | ∞ | 0 | ||
| 9 | 1 | 0 | 0 | ∞ | ||
| hi | 1 | 0 | 0 | 0 | 1 | |
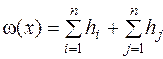 =17+1=18
=17+1=18
Таблица 11 «Расчет оценок для нулевых элементов»
| Пункты маршрута | А | 5 | 8 | 9 |
| А | ∞ | 0 4 |
4 |
4 |
| 5 | 0 4 |
∞ | 0 0 |
0 0 |
| 8 | 4 |
0 0 |
∞ | 0 0 |
| 9 | 4 |
0 0 |
0 0 |
∞ |
Так как в двух клетках наибольшие оценки одинаковы, выбираем любую. В данном случае – это клетка на пересечении строки А (k =А ) и столбца 5 (s = 5), вычеркиваем эту строку и столбец.
От начальной вершины "все решения" проводим ответвление вершин ks
и ![]() с нижними границами:
с нижними границами:
ω(А – 5) = 18+2 =22
______
ω(А – 5) = 18+2 =22
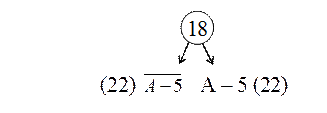
Таблица 12 «Приведение матрицы усеченной на строку А и столбец 5»
| Пункты маршрута | А | 8 | 9 | hi |
| 5 | ∞ | 0 | 0 | 0 |
| 8 | 0 | ∞ | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 |
| h j | 4 | 0 | 0 | - |
Таблица 13 «Определение оценок для усеченной матрицы»
| Пункты маршрута | А | 8 | 9 |
| 5 | ∞ | 0 0 |
0 0 |
| 8 | 0 0 |
∞ | 0 0 |
| 9 | 0 0 |
0 0 |
∞ |
Выбираем ячейку 5-9.
Таблица 13 «Матрица 2 х 2 для метода «ветвей и границ»»
| Пункты маршрута | А | 8 |
| 8 | 0 ∞ |
∞ |
| 9 | 0 0 |
0 ∞ |
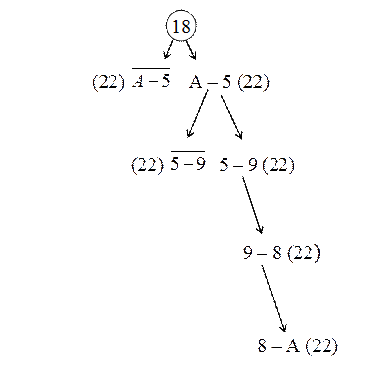
Сделаем проверку. Просуммируем соответствующие расстояния между пунктами: 5+4+4+9=22.
Маршрут А2.
Таблица 14 «Матрица кратчайших расстояний для маршрута от грузоотправителя А2»
| Пункты маршрута | А | 1 | 2 | 4 | 7 | 10 |
| А | 6 | 9 | 12 | 5 | 13 | |
| 1 | 6 | 3 | 7 | 6 | 8 | |
| 2 | 9 | 3 | 5 | 8 | 7 | |
| 4 | 12 | 7 | 5 | 9 | 2 | |
| 7 | 5 | 6 | 8 | 9 | 9 | |
| 10 | 13 | 8 | 7 | 2 | 9 |
Таблица 15 «Матрица кратчайших расстояний, приведенная по строкам»
| Пункты маршрута | А | 1 | 2 | 4 | 7 | 10 | hi |
| А | 1 | 4 | 7 | 0 | 8 | 5 | |
| 1 | 3 | 0 | 4 | 3 | 5 | 3 | |
| 2 | 5 | 0 | 2 | 5 | 4 | 3 | |
| 4 | 10 | 5 | 3 | 7 | 0 | 2 | |
| 7 | 0 | 1 | 3 | 4 | 4 | 5 | |
| 10 | 11 | 6 | 5 | 0 | 7 | 2 | |
| Итого: | 17 | ||||||
Таблица 16 «Матрица кратчайших расстояний, приведенная по столбцам»
| Пункты маршрута | А | 1 | 2 | 4 | 7 | 10 | Итого: |
| А | 1 | 4 | 7 | 0 | 8 | ||
| 1 | 3 | 0 | 4 | 3 | 5 | ||
| 2 | 6 | 0 | 2 | 5 | 4 | ||
| 4 | 10 | 5 | 3 | 7 | 0 | ||
| 7 | 0 | 1 | 3 | 4 | 4 | ||
| 10 | 11 | 6 | 5 | 0 | 7 | ||
| h j | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
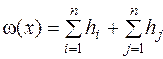 =17+0=17
=17+0=17
Таблица 17 «Расчет оценок для нулевых элементов»
| Пункты маршрута | А | 1 | 2 | 4 | 7 | 10 |
| А | 1 |
4 | 7 | 0 6 |
8 | |
| 1 | 3 | 0 6 |
4 | 3 | 5 | |
| 2 | 6 | 0 3 |
2 | 5 | 4 | |
| 4 | 10 |
5 | 3 | 7 | 0 7 |
|
| 7 | 0 4 |
1 | 3 | 4 | 4 | |
| 10 | 11 |
6 | 5 | 0 7 |
7 |
От начальной вершины "все решения" проводим ответвление вершин ks
и ![]() с нижними границами:
с нижними границами:
ω(4 – 10) = 23+7 =30
______
ω(4 – 10) = 23+7 =30
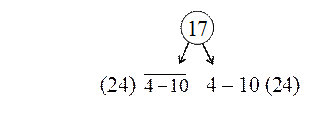
Таблица 18 «Приведение матрицы усеченной на строку 4 и столбец 10»
| Пункты маршрута | А | 1 | 2 | 4 | 7 | hi |
| А | 1 | 4 | 5 | 0 | 0 | |
| 1 | 3 | 0 | 2 | 3 | 0 | |
| 2 | 6 | 0 | 0 | 5 | 0 | |
| 7 | 0 | 1 | 3 | 2 | 0 | |
| 10 | 6 | 1 | 0 | 2 | 5 | |
| h j | 0 | 0 | 0 | 2 | 0 | - |
Таблица 19 «Определение оценок для усеченной матрицы»
| Пункты маршрута | А | 1 | 2 | 4 | 7 |
| А | 1 | 4 | 5 | 0 3 |
|
| 1 | 3 | 0 2 |
2 | 3 | |
| 2 | 6 | 0 1 |
0 2 |
5 | |
| 7 | 0 4 |
1 | 3 | 2 | |
| 10 | 6 | 1 | 0 1 |
|
2 |
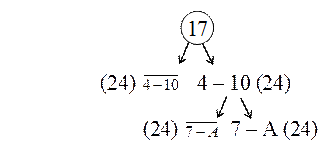
Таблица 20 «Определение оценок для усеченной матрицы»
| Пункты маршрута | А | 1 | 2 | 4 |
| 1 | 0 5 |
0 2 |
2 | |
| 2 | 3 | 0 1 |
0 2 |
|
| 7 |
|
0 1 |
2 | 1 |
| 10 | 6 | 1 | 0 1 |
|
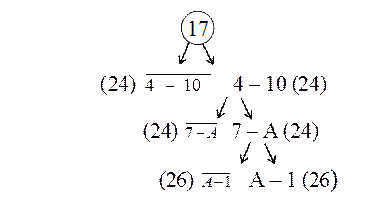
Таблица 21 «Определение оценок для усеченной матрицы»»
| Пункты маршрута | 1 | 2 | 4 |
| 2 | 3 | ∞ | 0 4 |
| 7 | 0 0 |
2 | 1 |
| 10 | 1 |
0 3 |
∞ |
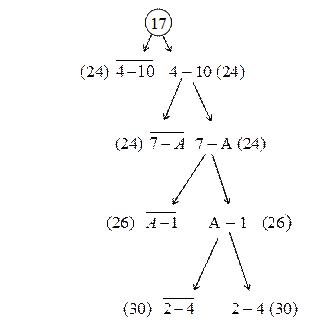
Таблица 22 «Матрица 2 х 2 для метода «ветвей и границ»»
| Пункты маршрута | 1 | 2 |
| 7 | 0 3 |
2 |
| 10 | 1 | 0 3 |
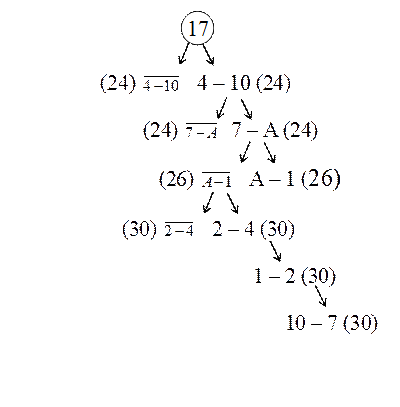
Сделаем проверку. Просуммируем соответствующие расстояния между пунктами: 6+3+5+2+9+5=30.
Маршрут Б
Таблица 23 «Матрица кратчайших расстояний для маршрута от грузоотправителя Б»
| Пункты маршрута | Б | 3 | 6 |
| Б | 9 | 6 | |
| 3 | 9 | 5 | |
| 6 | 6 | 5 |
Таблица 24 «Матрица кратчайших расстояний, приведенная по строкам»
| Пункты маршрута | Б | 3 | 6 | hi |
| Б | 3 | 0 | 6 | |
| 3 | 4 | 0 | 5 | |
| 6 | 1 | 0 | 5 | |
| Итого: | 16 | |||
Таблица 25 «Матрица кратчайших расстояний, приведенная по столбцам»
| Пункты маршрута | Б | 3 | 6 | Итого: |
|
| Б | ∞ | 3 | 0 | ||
| 3 | 3 | ∞ | 0 | ||
| 6 | 0 | 0 | ∞ | ||
| hi | 1 | 0 | 0 | 1 | |
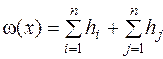 =16+1=17
=16+1=17
Таблица 26 «Расчет оценок для нулевых элементов»
| Пункты маршрута | Б | 3 | 6 |
| Б | ∞ | 3 |
0 3 |
| 3 | 3 |
∞ | 0 3 |
| 6 | 0 3 |
0 3 |
∞ |
Выбираем ячейку Б-6. От начальной вершины "все решения" проводим ответвление вершин ks
и ![]() с нижними границами:
с нижними границами:
ω(Б – 6) = 17+3 =20
______
ω(Б – 6) = 17+3 =20
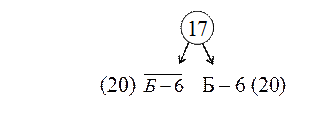
Таблица 27 «Приведение матрицы усеченной на строку Б и столбец 6»
| Пункты маршрута | Б | 3 | hi |
| 3 | 3 | ∞ | 0 |
| 6 | ∞ | 0 | 0 |
| h j | 3 | 0 | - |
Таблица 28 «Определение оценок для усеченной матрицы»
| Пункты маршрута | Б | 3 |
| 3 | 0 ∞ |
∞ |
| 6 | ∞ |
0 ∞ |
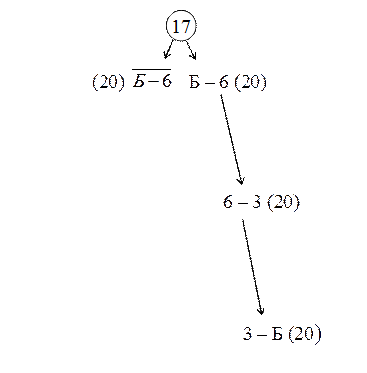
Сделаем проверку. Просуммируем соответствующие расстояния между пунктами: 6+5+9=20.
Пробег с грузом (L г ), общий пробег (L о ) и транспортная работа (Р ) для развозочных маршрутов определяются по следующим формулам:
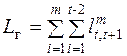
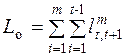
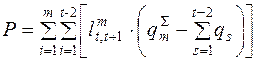
где m – количество развозочных маршрутов;
t – количество пунктов на маршруте (пункт погрузки учитывается два раза);
![]() – пробег между соседними пунктами маршрута, км;
– пробег между соседними пунктами маршрута, км;
![]() - суммарный объем перевозок на m
-ом маршруте, т;
- суммарный объем перевозок на m
-ом маршруте, т;
qs – объем груза, выгружаемый в s -ом пункте, т.
Lг = 13+25+11=49 км
Lо = 22+30+20=72 км
РА1 = 5*10,94+4*6,15+4*1,63=85,82 ткм
РА2 =7*12,56+3*8,32+18*5,28+9*1,46=221ткм
РБ =6*6,03+5*4,40=80,18 ткм
Р = РА1 + РА2 + РБ = 85,82+221+80,18=387 ткм
Сравним полученные данные и технико-эксплуатационные показатели по маятниковым маршрутам.
Таблица 29 «Сравнение технико-эксплутационных показателей»
| Показатель | Пробег с грузом, км | Общий пробег, км | Транспортная работа, ткм |
| после решения транспортной задачи | 83 | 166 | 221,78 |
| после решения задачи маршрутизации | 49 | 72 | 387 |
Вывод: за счет использования кольцевых маршрутов подвижной состав используется более эффективно. Снижается затраты на его использование. В то же время транспортная работа возрастает, так как транспортному средству приходится перевозить большой объем товара на первых этапах.
5. Оценка интервалов времени прибытия и отправления транспортных средств для каждого пункта маршрутов
Оценка времени доставки груза производиться по формулам:
для верхней границы ![]() для нижней границы
для нижней границы![]()
где ![]() - среднее значение доставки объема груза, ч;
- среднее значение доставки объема груза, ч;
Т н – время начала работы, ч (устанавливается студентом самостоятельно).
![]() – среднее квадратическое отклонение времени доставки груза, ч;
– среднее квадратическое отклонение времени доставки груза, ч;
![]() – квантиль нормального распределения, соответствующий вероятности P
(равен 1,5).
– квантиль нормального распределения, соответствующий вероятности P
(равен 1,5).
1) Определение интервалов времени прибытия и отправления на маршруте А1.
Таблица 30«Объем перевозок и расстояния между пунктами маршрута»
| Пункты | А | 5 | 9 | 8 |
| li ,i +1 | 5 | 4 | 4 | 9 |
| Объем груза под погрузку (разгрузку), т | 10,94 | 4,79 | 4,52 | 1,63 |
Средние значения времени погрузки и разгрузки для одного автомобиля рассчитывается исходя из нормативов: 30 мин. на первую тону и по 15 мин. на каждую следующую полную или неполную тонну. Коэффициенты вариации составляют 0,6 для времени погрузки и 0,7 для времени разгрузки.
Время погрузки в пункте А:
t п А = 30 +10*15=180 мин
Среднеквадратическое отклонение времени погрузки в пункте А:
σt п А = 0,6*180=108 мин
Время движения t дв =5/17,9=0,28*60≈17 мин
В данном случае среднеквадратическое отклонение времени доставки зависит только от погрузки, поэтому:
σt
сА
= 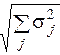 = σt
п А
=108 мин
= σt
п А
=108 мин
Верхняя и нижняя границы интервала:
Тот в = Тн + Тс А + 1,5* σtсА =540+180+1,5*108=882 мин (15 ч 42 мин)
Тот н = Тн + Тс А - 1,5* σtсА =540+180-1,5*108=558 мин (9 ч 18 мин)
Автомобиль покинет пункт А после погрузки по среднему значению в 12:00.
- Прибытие в пункт 5
Время движения из пункта А в пункт 5:
t дв 5 =5/17,9=0,28*60≈17 мин
σt дв 5 =0,3*17=5 мин
Среднее время доставки груза в пункт 5:
____ __
Т с пр6 = Т с А + t дв 5 =720+17=737 мин (12 ч 17 мин)
Отклонение времени доставки груза в пункт 5:
σТс пр5 =√1082 +52 =108 мин
Верхняя и нижняя границы интервала:
Тпр в = Тс пр5 + 1,5* σТс пр5 =737+1,5*108=899 мин (14 ч 59 мин)
Тпр н = Тс пр5 - 1,5* σТс пр5 =737-1,5*108=575 мин (9 ч 35 мин)
- Отправление из пункта 5
Время разгрузки груза в пункте 5:
t р 5 =30+4*15=90 мин
σt р 5 =0,7*90=63 мин
Среднее время отправления из пункта 5:
___ ____
Т с от5 = Т с пр5 + t р 5 =737+90=827 мин (13 ч 47 мин)
Отклонение времени отправления из пункта 5:
σТс от5 =√1082 +52 +632 =125 мин
Верхняя и нижняя границы интервала:
Тот в = Тс от5 + 1,5* σТс от5 =827+1,5*125=1014 мин (16 ч 54 мин)
Тот н = Тс от5 - 1,5* σТс от5 =827-1,5*125=640 мин (10 ч 40 мин)
- Прибытие в пункт 9
Время движения из пункта 5 в пункт 9:
t дв 9 = 4/17,9=0,22*60≈13 мин
σt дв 9 = 0,3*13=4 мин
Среднее время доставки груза в пункт 9:
____ __
Т с пр9 = Т с А + t дв 9 =827+13=840 мин (14 ч 00 мин)
Отклонение времени доставки груза в пункт 9:
σТс пр9 =√1082 +52 +632 +42 =125 мин
Верхняя и нижняя границы интервала:
Тпр в = Т с пр9 + 1,5* σТс пр9 =840+1,5*125=1027 мин (17 ч 7 мин)
Тпр н = Т с пр9 - 1,5* σТс пр9 =840-1,5*125=653 мин (10 ч 53 мин)
- Отправление из пункта 9
Время разгрузки груза в пункте 9:
t р 9 =30+4*15=90 мин
σt р 9 =0,7*90=63 мин
Среднее время отправления из пункта 9:
___ ____
Т с от9 = Т с пр9 + t р 9 =840+90=930 мин (15 ч 30 мин)
Отклонение времени отправления из пункта 9:
σТс от9 =√1082 +52 +632 +42 +632 =140 мин
Верхняя и нижняя границы интервала:
Тот в = Тс от9 + 1,5* σТс от9 =930+1,5*140=1070 мин (17 ч 50 мин)
Тот н = Т с от9 - 1,5* σТс от9 =930-1,5*140=720 мин (12 ч 00 мин)
- Прибытие в пункт 8
Время движения из пункта 9 в пункт 8:
t дв 8 = 4/17,9=0,22*60≈13 мин
σt дв 8 = 0,3*13=4 мин
Среднее время доставки груза в пункт 8:
Т с пр8 = Т с 8 + t дв 8 =930+13=943 мин (15 ч 43 мин)
Отклонение времени доставки груза:
σТс пр8 =√1082 +52 +632 +42 +632 +42 =140 мин
Верхняя и нижняя границы интервала:
Тпр в = Т с пр8 + 1,5* σТс пр8 =943+1,5*140=1153 мин (19 ч 13 мин)
Тпр н = Т с пр8 - 1,5* σТс пр8 =943-1,5*140=733 мин (12 ч 13 мин)
- Отправление из пункта 8
Время разгрузки груза в пункте 8:
t р 8 =30+1*15=45 мин
σt р 8 =0,7*45=31,5 мин
Среднее время отправления из пункта 8:
___ ____
Т с от8 = Т с пр8 + t р 8 =943+45=988 мин (16 ч 28 мин)
Отклонение времени отправления из пункта 8:
σТс от 8 =√1082 +52 +632 +42 +632 +42 +31,52 =143 мин
Верхняя и нижняя границы интервала:
Тот в = Тс от8 + 1,5* σТс от8 =988+1,5*143=1202 мин (17 ч 23 мин)
Тот н = Т с от8 - 1,5* σТс от8 =988-1,5*143=774 мин (12 ч 54 мин)
- Прибытие в пункт А
Время движения из пункта 8 в пункт А:
t дв А = 9/17,9=0,5*60≈30 мин
σt дв А = 0,3*30=9 мин
Среднее время прибытия в пункт А:
Т с прА = Т с А + t дв А =988+30=1018 мин (17 ч 58 мин)
Отклонение времени прибытия в пункт А:
σТс прА =√1082 +52 +632 +42 +632 +42 +31,52 +92 =144 мин
Верхняя и нижняя границы интервала:
Тпр в = Т с прА + 1,5* σТс прА =1018+1,5*144=1234 мин (20 ч 34 мин)
Тпр н = Т с прА - 1,5* σТс прА =1018-1,5*144=802 мин (13 ч 22 мин)
Таблица 31 «Оценка времени прибытия и отправления в пункты маршрута»
| Пункт | Время прибытия | Время отправления | ||||
| А | 9-00 | - | - | 12-00 | 15-42 | 9-18 |
| 5 | 12-17 | 14-59 | 9-35 | 13-47 | 16-54 | 10-40 |
| 9 | 14-00 | 17-07 | 10-53 | 15-30 | 17-50 | 12-00 |
| 8 | 15-43 | 19-13 | 12-13 | 16-28 | 17-23 | 12-54 |
| А | 17-58 | 20-34 | 13-22 | - | - | - |
3) Определение интервалов времени прибытия и отправления на маршруте А2.
Таблица 32 «Объем перевозок и расстояния между пунктами маршрута»
| Пункты | А | 1 | 2 | 4 | 7 | 10 |
| li ,i +1 | 7 | 3 | 5 | 9 | 9 | 13 |
| Объем груза под погрузку (разгрузку), т | 12,56 | 4,24 | 2,30 | 0,74 | 3,82 | 1,46 |
- Отправление из пункта А
Время погрузки в пункте А:
t п А = 30 +12*15=210 мин
Среднеквадратическое отклонение времени погрузки:
σt п А = 0,6*210=126 мин
Время движения t дв =7/17,9=0,39*60≈23 мин
В данном случае среднеквадратическое отклонение времени доставки зависит только от погрузки, поэтому:
σt
сА
= 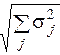 = σt
п А
=126 мин
= σt
п А
=126 мин
Верхняя и нижняя границы интервала:
Тот в = Тн + Тс А + 1,5* σtсА =480+210+1,5*126=879 мин (14 ч 39 мин)
Тот н = Тн + Т с А - 1,5* σt сА =480+210-1,5*126=501 мин (8 ч 21 мин)
Автомобиль покинет пункт А после погрузки по среднему значению в 11:30.
- Прибытие в пункт 1
Время движения из пункта А в пункт 1:
t дв 1 =7/17,9=0,39*60≈23 мин
σt дв 1 =0,3*23=7 мин
Среднее время доставки груза в пункт 1:
____ __
Т с пр1 = Т с А + t дв 1 =690+23=713 мин (11 ч 53 мин)
Отклонение времени доставки груза в пункт 1:
σТс пр1 =√1262 +72 =126 мин
Верхняя и нижняя границы интервала:
Тпр в = Тс пр1 + 1,5* σТс пр1 =713+1,5*126=902 мин (15 ч 2 мин)
Тпр н = Т с пр1 - 1,5* σТс пр1 =713-1,5*126=524 мин (8 ч 44 мин)
- Отправление из пункта 1
Время разгрузки груза в пункте 1:
t р 1 =30+4*15=90 мин
σt р 1 =0,7*90=63 мин
Среднее время отправления из пункта 1:
___ ____
Т с от1 = Т с пр1 + t р 1 =713+90=803 мин (13 ч 23 мин)
Отклонение времени отправления из пункта 1:
σТс от1 =√1262 +72 +632 =141 мин
Верхняя и нижняя границы интервала:
Тот в = Тс от1 + 1,5* σТс от1 =803+1,5*141=1014 мин (16 ч 54 мин)
Тот н = Т с от1 - 1,5* σТс от1 =803-1,5*141=592 мин (9 ч 52 мин)
- Прибытие в пункт 2
Время движения из пункта 1 в пункт 2:
t дв 2 =3/17,9=0,16*60≈10 мин
σt дв 2 =0,3*10=3 мин
Среднее время доставки груза в пункт 2:
Т с пр2 = Т с 1 + t дв 2 =803+10=823 мин (13 ч 43 мин)
Отклонение
29-04-2015, 02:40
