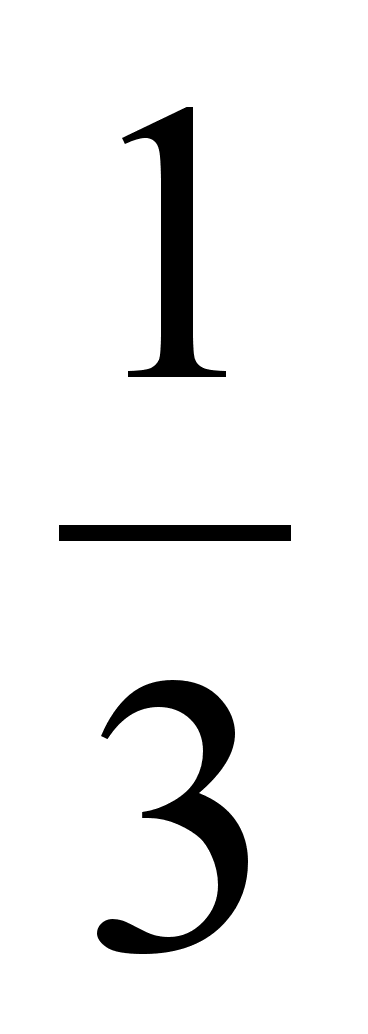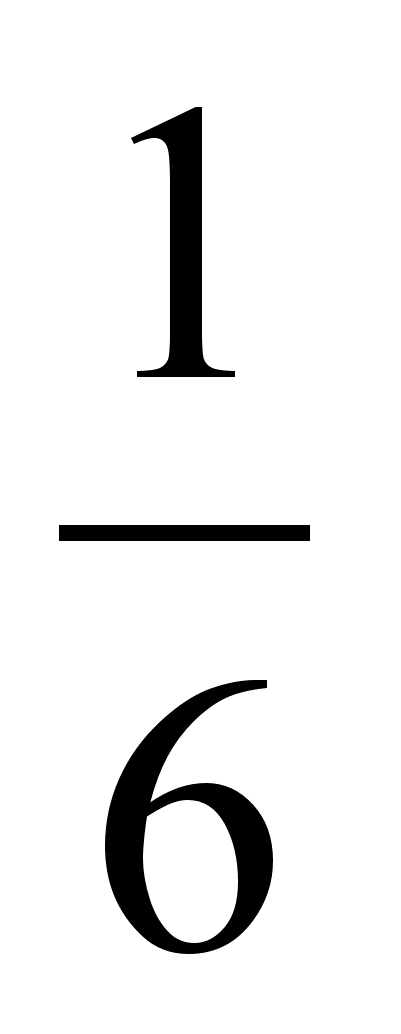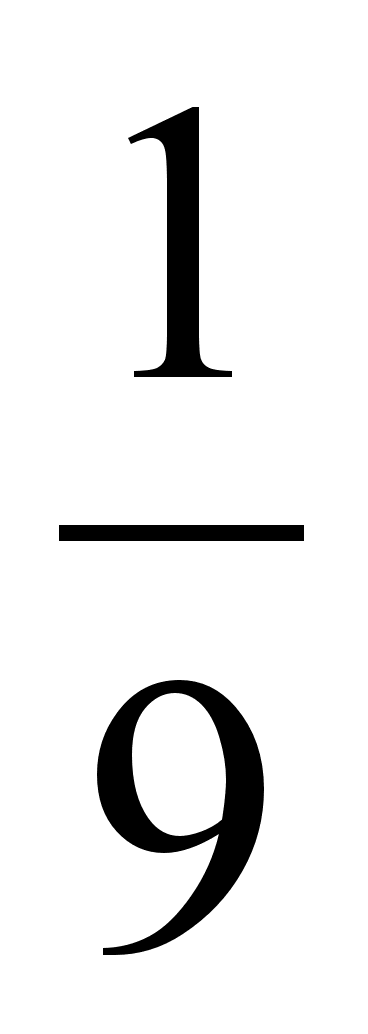- Задание.
Решить прямую задачу размерной цепи механизма толкателя, изображённого на рисунке 1.1., методами максимума-минимума и вероятностным. Способ решения стандартный,
А3
= 100 мм

Рис 1.1.
А2 А1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
А![]()
![]()
![]()
![]()
![]() 3
3
![]()
![]()

![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
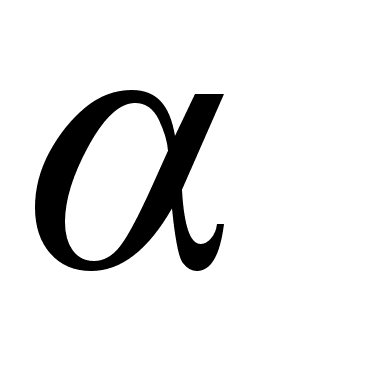
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() А3
А3
![]()
А4 А5 А
![]()
![]()
![]()
![]()
 (
Схема механизма
толкателя )
(
Схема механизма
толкателя )
Обозначения: А1 – длина поршня;
А2 – радиус поршня;
А3 – расстояние между осями отверстий в толкателе;
А4 – расстояние от торца крышки до оси отверстия в ней;
А5 – длина корпуса;
А - вылет
поршня за пределы
корпуса;
- вылет
поршня за пределы
корпуса;
Таблица 1.1. ( исходные данные )
|
А1, мм |
А2,мм |
А3,мм |
А4,мм |
А5,мм |
А |
|
%,риска |
|
|
20 |
100 |
110 |
153 |
А |
420 |
1,0 |
Аi – номинальные размеры составляющих звеньев,
А - предельное
отклонение
размера
- предельное
отклонение
размера
( А’3
= А3
Сos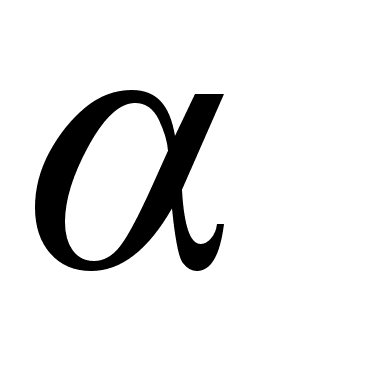 )
)
Таблица 1.2.
|
|
| ||
|
Коэффициент
относительного
рас-сеивания
взятый в квадрате
(
|
|
|
|
- Краткая теория.
- Основные определения.
Размерная цепь – совокупность размеров, образующих замкнутый контур и непосредственно участвующих в решении поставленной задачи. Размерные цепи бывают плоские, параллельные и пространственные. Замкнутость – является обязательным условием размерной цепи.
- Размерные цепи состоят из звеньев:
![]()
ЗВЕНЬЯ
![]()
![]()


СОСТАВЛЯЮЩИЕ ЗАМЫКАЮЩИЕ
Аi, Вi ИСХОДНЫЕ
![]()
![]() Ai
,
BI
Ai
,
BI
![]()
![]()
УВЕЛИЧИВАЮЩИЕ УМЕНЬШАЮЩИЕ
Замыкающий размер ( звено ) – размер ( звено ), которое получается при обработке деталей или при сборке узла последним.
Увеличивающий размер ( звено ) – размер ( звено ), при увеличении которого замыкающий размер увеличивается.
Для плоских
параллельных
размерных цепей
 =
+1
=
+1
 Где:
Где:
 =
=
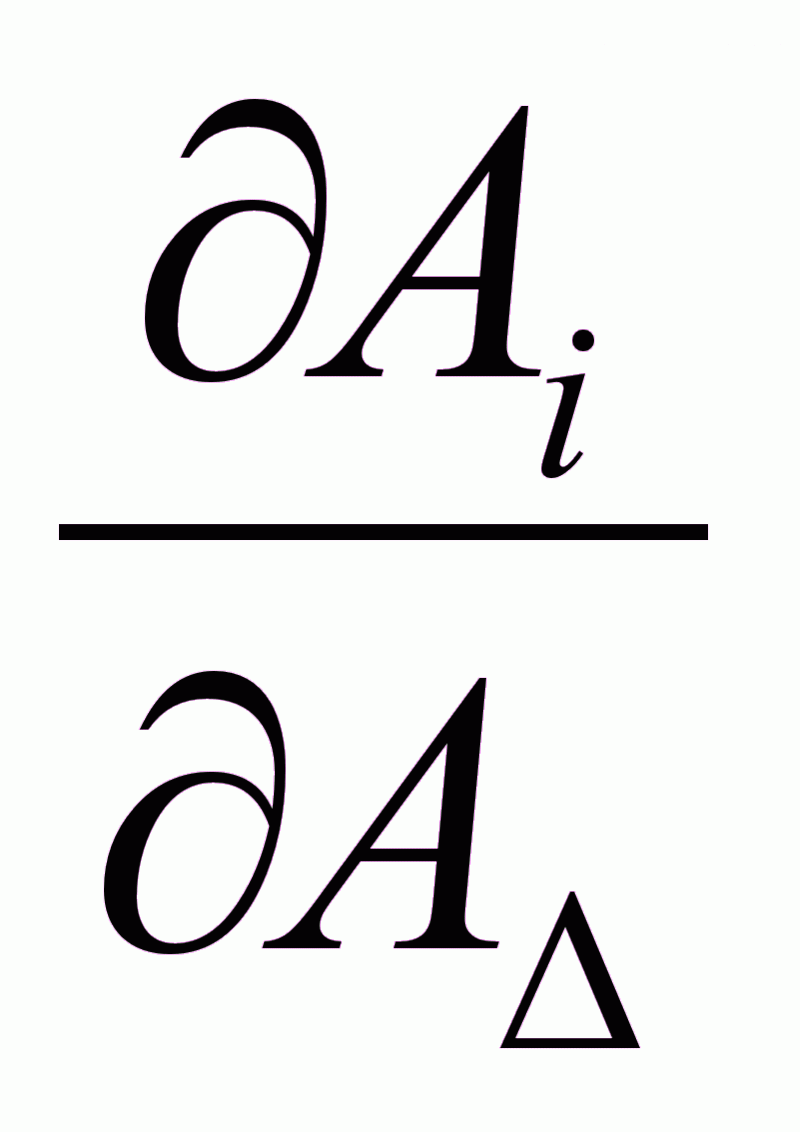 - коэффициент
влияния.
- коэффициент
влияния.
Уменьшающий размер – размер, при увеличении которого замыкающий размер уменьшается.
 = -1
= -1
- Задачи размерных цепей.
Существует две задачи для размерных цепей: прямая и обратная.
Обратная задача заключается в определении номинального размера, координат середины поля допуска и предельных отклонений замыкающего звена при заданных аналогичных значениях составляющих звеньев.
( синтез ) заключается в заключении номинальных размеров, координат середин полей допусков, допусков и предельных отклонений составляющих звеньев по заданным аналогичным значениям исходного звена.
Прямая задача не решается однозначно.
2.2.1.1. Основные закономерности размерных цепей.
Связь номинальных размеров.
А =
=
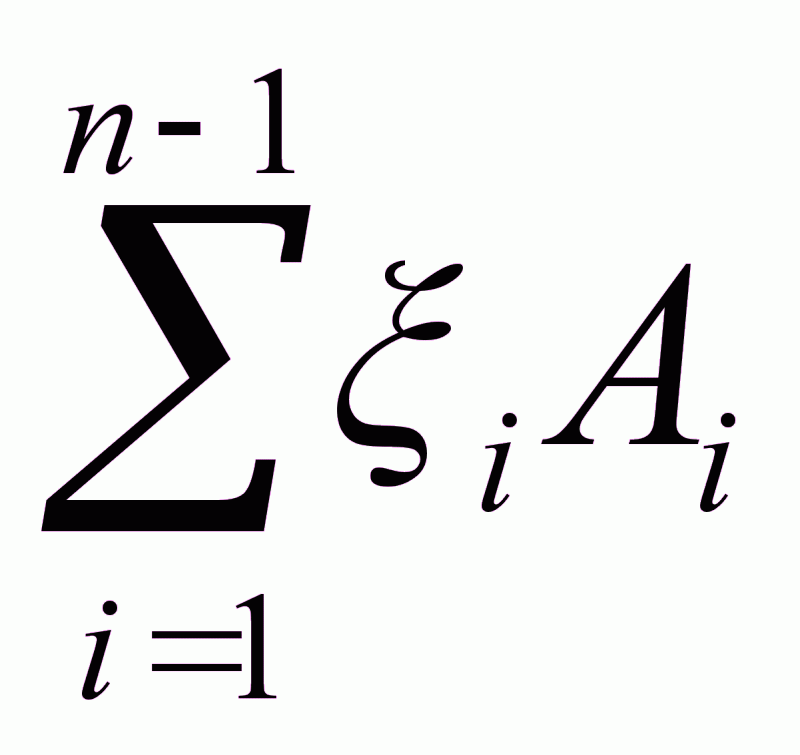
Где:
А - номинальный
размер исходного
звена;
- номинальный
размер исходного
звена;
А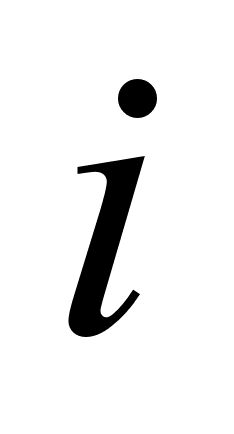 - номинальный
размер составляющих
звеньев;
- номинальный
размер составляющих
звеньев;
 i
- коэффициент
влияния;
i
- коэффициент
влияния;
n-1 – количество составляющих звеньев.
Связь координат середин полей допусков:

=
=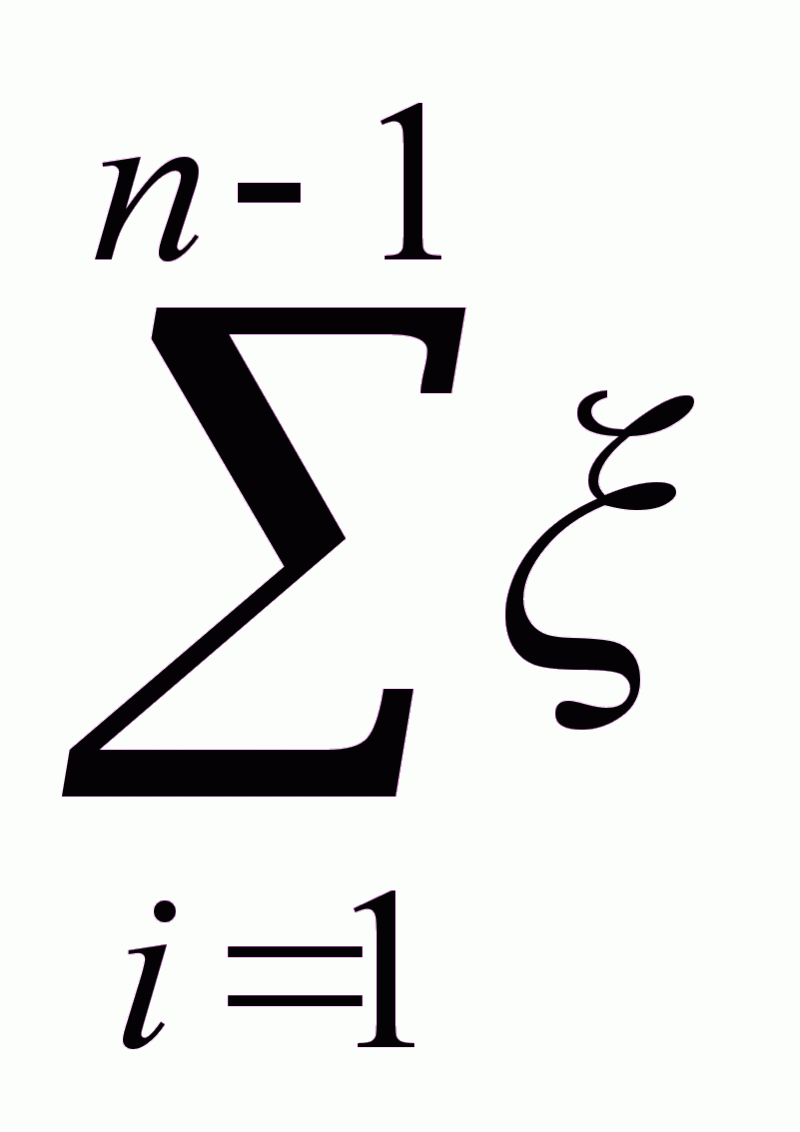 i
i
 0i
, где
0i
, где
 0i
- координата
середины поля
допуска i-го
составляющего
0i
- координата
середины поля
допуска i-го
составляющего
звена

- координата
середины поля
допуска замыкающего
звена.
- координата
середины поля
допуска замыкающего
звена.
Связь допусков.
Метод максимума-минимума.
Т =
=
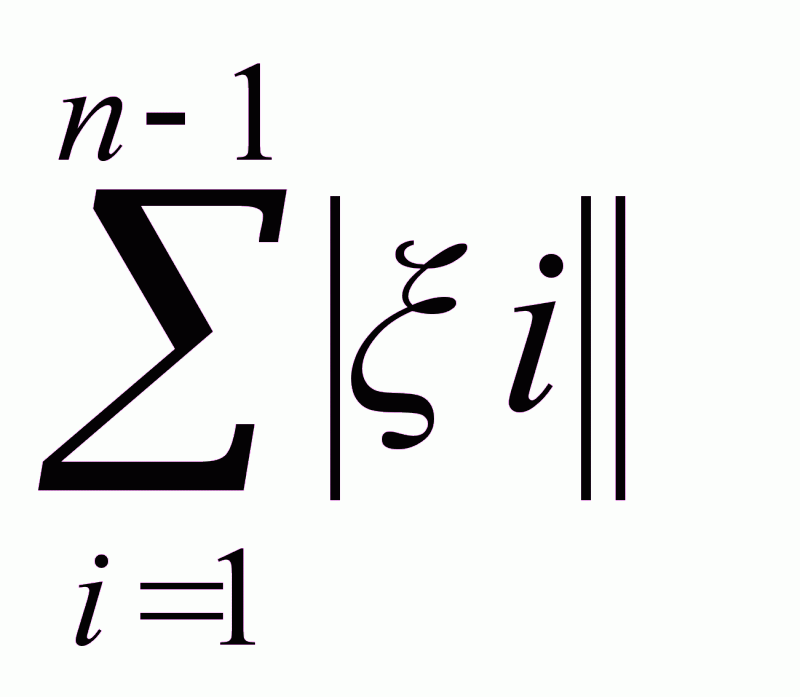 Тi
Тi
- Метод теоретико-вероятностный.
Т = t
= t
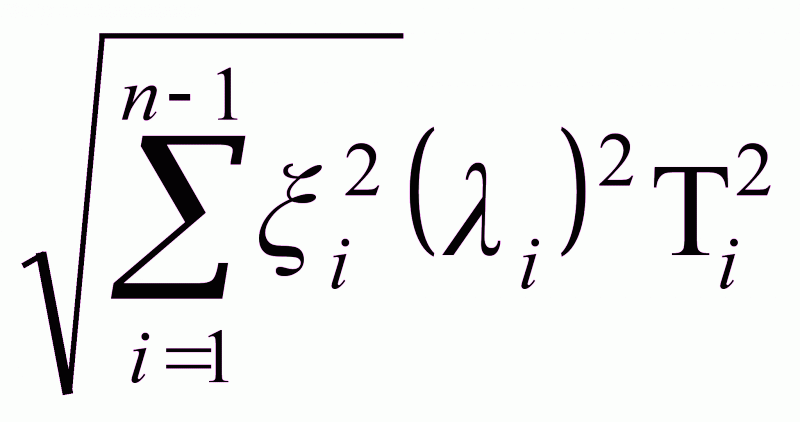 , где
, где
t - коэффициент риска, который выбирают с учетом заданного
процента риска р.
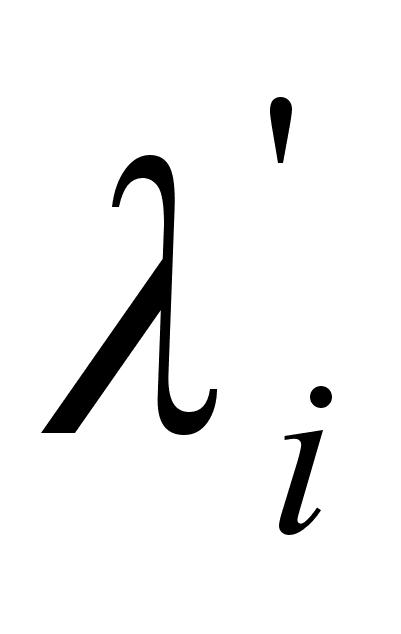 - коэффициент
относительного
рассеяния.
- коэффициент
относительного
рассеяния.
- Связь предельных размеров звеньев.
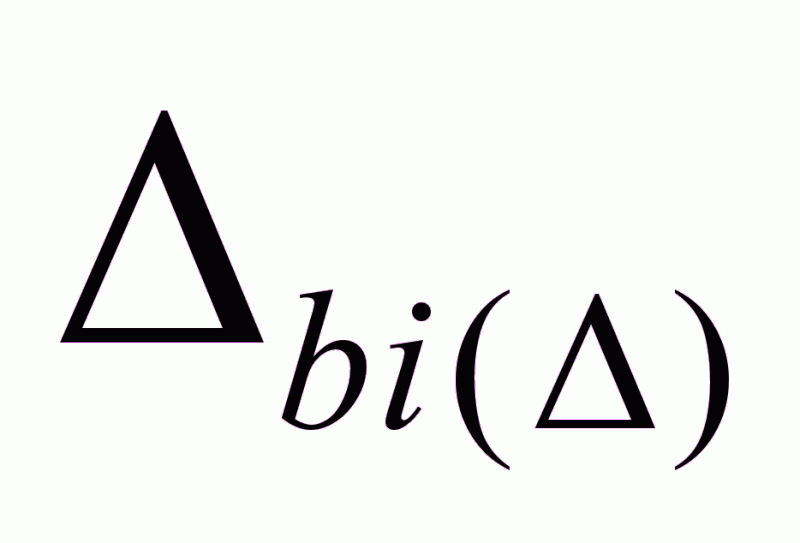 =
=
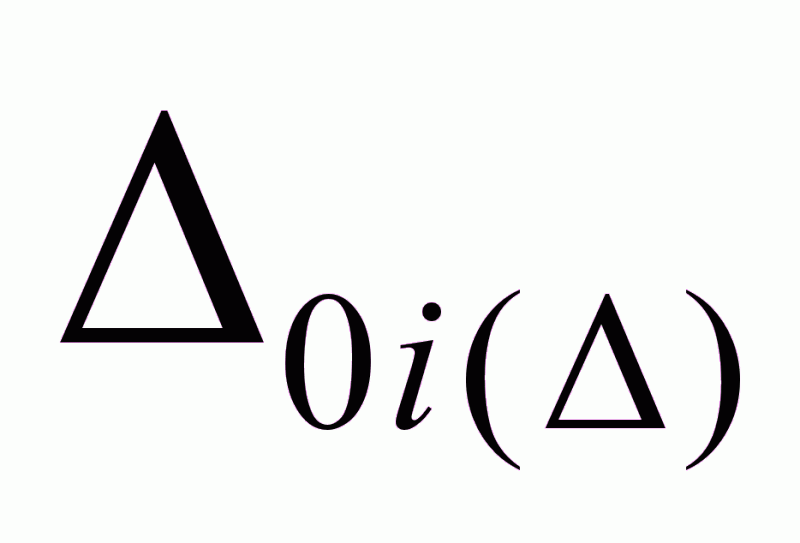 +
+
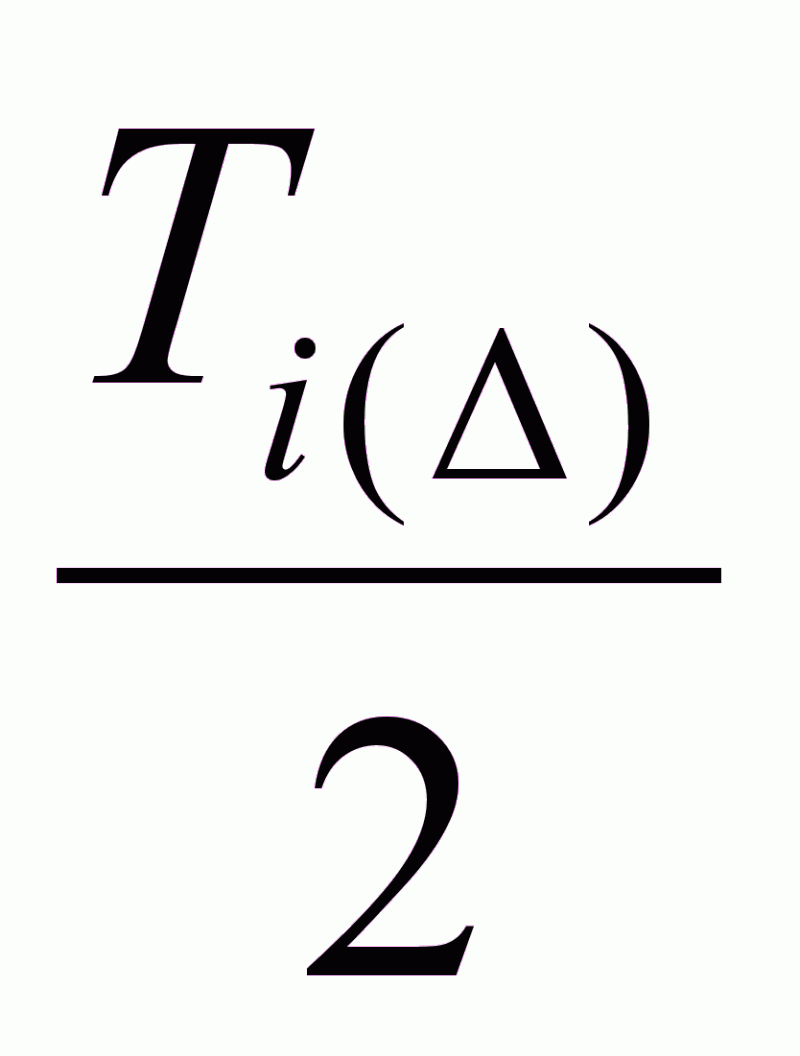
Способы решения прямой задачи.
- Способ равных допусков.
Его принимают, если несколько составляющих звеньев имеют один порядок и могут быть выполнены с примерно одинаковой точностью, т.е. :
Т1 = Т2 = Т3 = … = Тn-1
Для метода
max/min : Ti
=
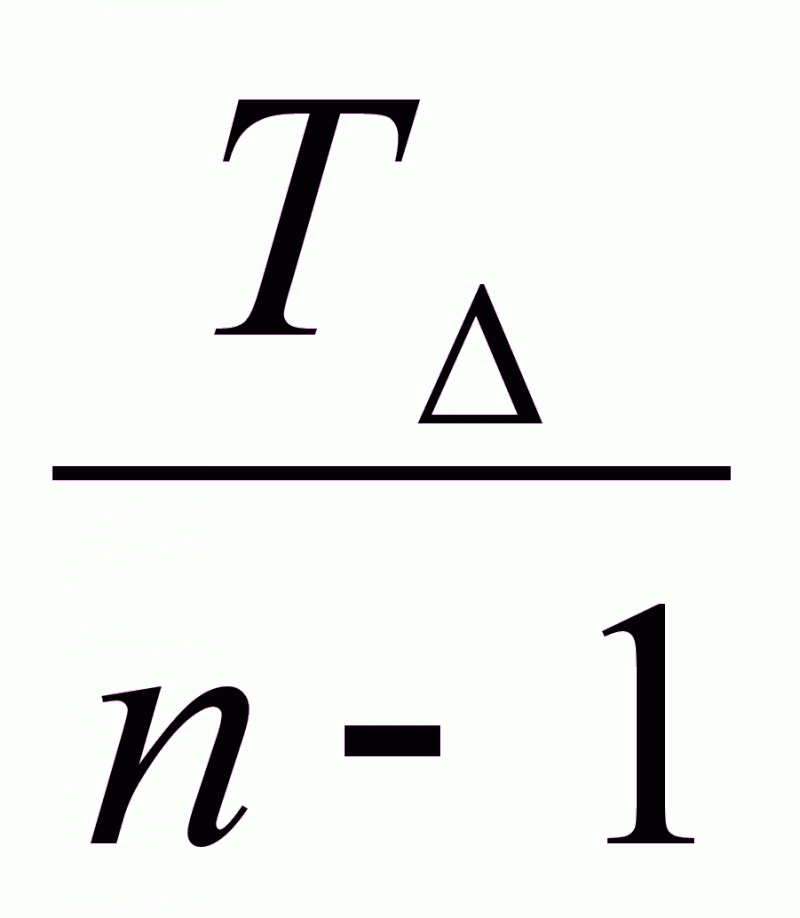
Для т/в
метода:
Тi
=
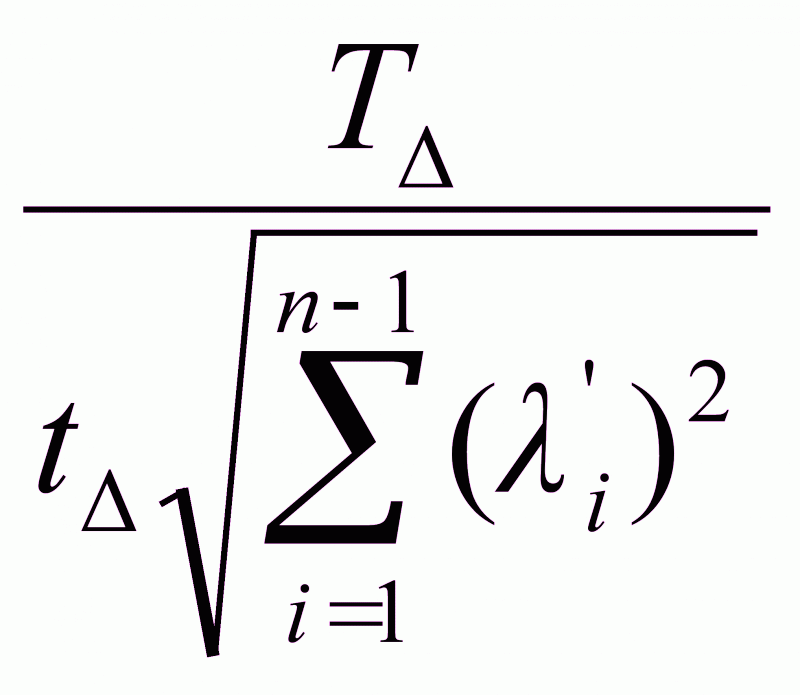
Расчетное
значение допусков
округляют до
стандартных
по ГОСТ
29-04-2015, 04:13

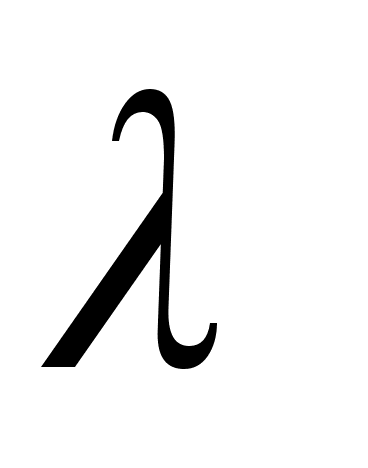 ’i
)2
’i
)2